基于符號動力學的倒鋸齒映射混沌檢測機理研究
楊 汝, 王燕芬, 馮錦澎
(廣州大學 物理與電子信息學院, 廣東 廣州 510006)
基于符號動力學的倒鋸齒映射混沌檢測機理研究
楊 汝, 王燕芬, 馮錦澎
(廣州大學 物理與電子信息學院, 廣東 廣州 510006)
以混沌系統的參數敏感性和初值敏感性為基礎,倒鋸齒映射為模型,按照符號動力學原理,建立符號序列空間,計算待測初值和零點的軌道空間距離求得待測值.令恒流源對電容進行充放電,分析設計具體的混沌檢測電路,成功地將倒鋸齒映射應用到混沌微弱信號檢測上.
倒鋸齒映射; 符號動力學; 微弱信號檢測
混沌研究已經從純理論研究走向應用研究,在氣象學、生物醫學、電子學方面取得十分有實用價值的成果[1-3],例如,將確定性混沌技術應用于風速和風力發電機的輸出功率預測,使預測時間從幾小時擴展到24 h,給風電運營商管理和能源調度提供了決策依據;又如將混沌控制技術應用于自發性癲癇的治療,有效地抑制它的發作頻率;再如混沌同步實現多個Boost變換器均流控制,也取得了初步的效果等.
初值敏感性是混沌的固有特性[4-6],初值敏感性是指當系統的結構參數穩定時,微小的初值變化就會使其運動軌跡之間呈現指數分離,反而言之,檢測運動軌跡之間的差異,就能知道初值的細微變化量.從符號動力學看,初值與系統運動軌跡在一定的時間內是一一對應的,初始值的細微變化量可以采用符號動力學分析方法高精度測量[7-9],從而可以應用于微弱信號的檢測.目前,基于混沌初值敏感性機理對微弱信號檢測研究,主要是以Duffing振子、Lorenz振子和倒鋸齒映射作為混沌動力學模型,以Duffing振子為模型的混沌檢測系統應用在金屬探測器[10],成功判斷金屬物質的存在,達到檢出金屬雜質的目的;在超聲波液位檢測中能提高檢測超聲波回波信號的精度[11],為超聲波液位檢測準確判斷液位高度提供了方便;在機械設備的齒輪故障檢測中能夠檢測出齒輪故障的幅值信[12].以Lorenz振子為模型的混沌檢測系統為檢測微弱正弦信號引出了另一條路[13];對數值天氣轉折期預報與氣候突變檢測、預測給出一種新理論和新方法[14].以倒鋸齒映射為模型的混沌動力系統則可以用于微弱信號的直接數字化測量[15],同時提高測量分辨率和靈敏度.
為此,本文以倒鋸齒映射為研究對象,基于符號動力學原理,建立符號序列空間,得到不同的初值下的運動軌道和符號序列;根據待測初值和零點的軌道空間距離計算得到待測值.最后分析設計具體的混沌檢測電路,數值仿真和電路實驗證明該方法應用在微弱信號檢測上不僅電路簡單,而且具有靈敏度和分辨率高的特性.
1 倒鋸齒映射模型
倒鋸齒映射模型也稱反移位映射模型[16],見圖1,其經典的迭代關系為
(1)
如果把移位映射的變化范圍限制到[0,1],
(2)
特別當參量k=2時,有
xn+1=1-2xn(mod1)
(3)
模運算(mod 1)的意思是,只保留計算結果的小數部分.對于保存在計算機里的二進制數,乘以2相當于向右移位1次.這時字長最右端空出的一位補零,而從左端移進去的(進位)1舍棄不要,即實現模運算(mod 1),得到的二進制取反加一產生補碼.這就是反移位映射的由來.
經過n次迭代后,一維映射的Lyapunov指數λ的的計算公式為
(4)
把式(2)代入式(3)求得λ=lnk,當k>1時,λ= lnk>0,此時該系統處于混沌狀態.本系統工作于k=2,此時倒鋸齒映射系統為混沌動力系統,其具有對初值條件的敏感依賴性,可用于混沌微弱信號檢測.
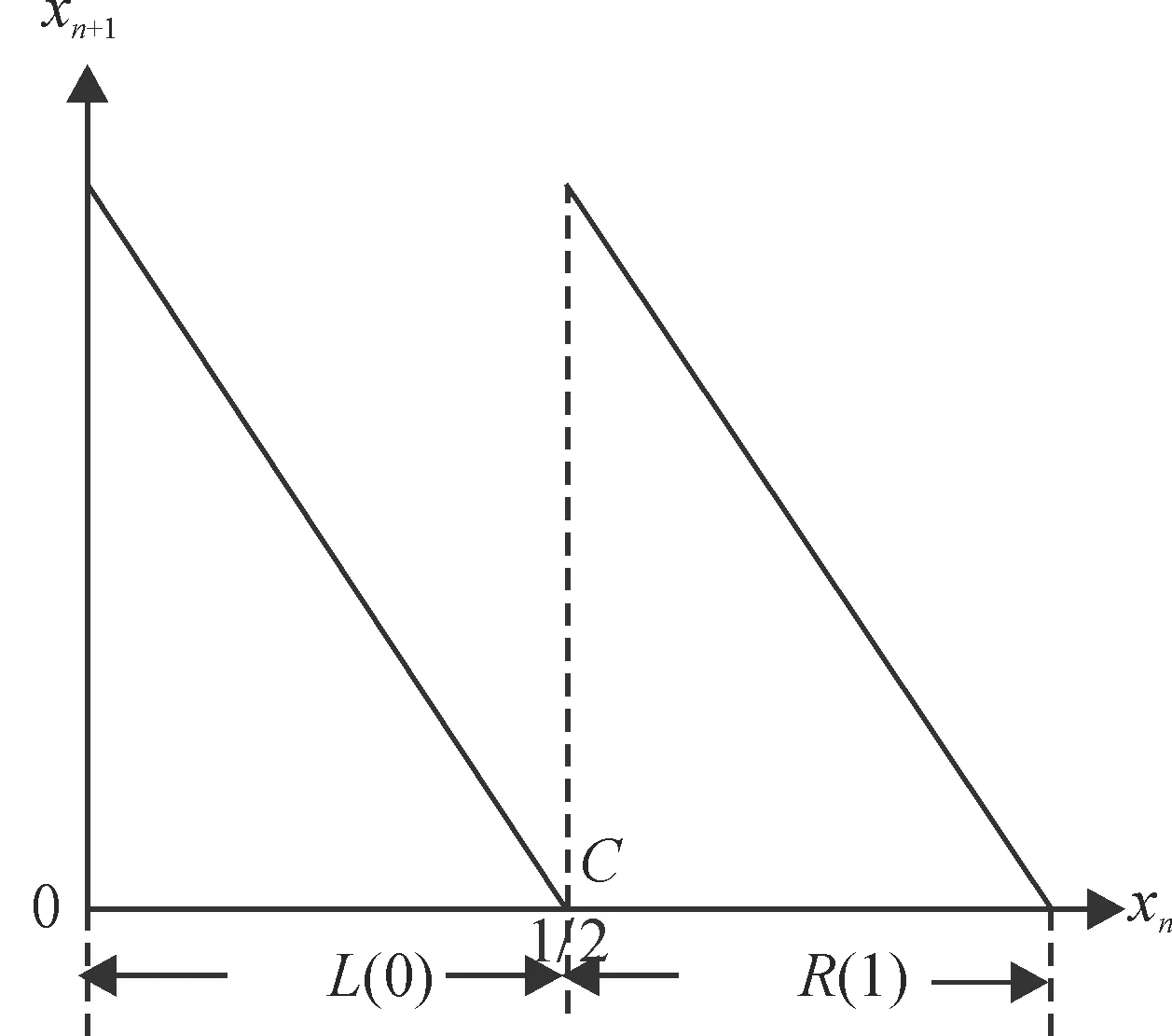
圖1 倒鋸齒映射Fig.1 The inverted saw-tooth map
2 一維映射符號動力學
給定區間上一點x0,以x0點為初始點進行迭代,可得到一條軌道:
x0,x1=f(x0),x2=f(x1),…xn=f(xn-1),…
(5)
從圖1可見,倒鋸齒映射模型有臨界點C.若xn落在臨界點C的右側,記為字母R,若落在臨界點C的左側,記為字母L.于是,由軌道(5)可得到一個符號序列[17]
s0s1s2…sn…
(6)
其中,
(7)
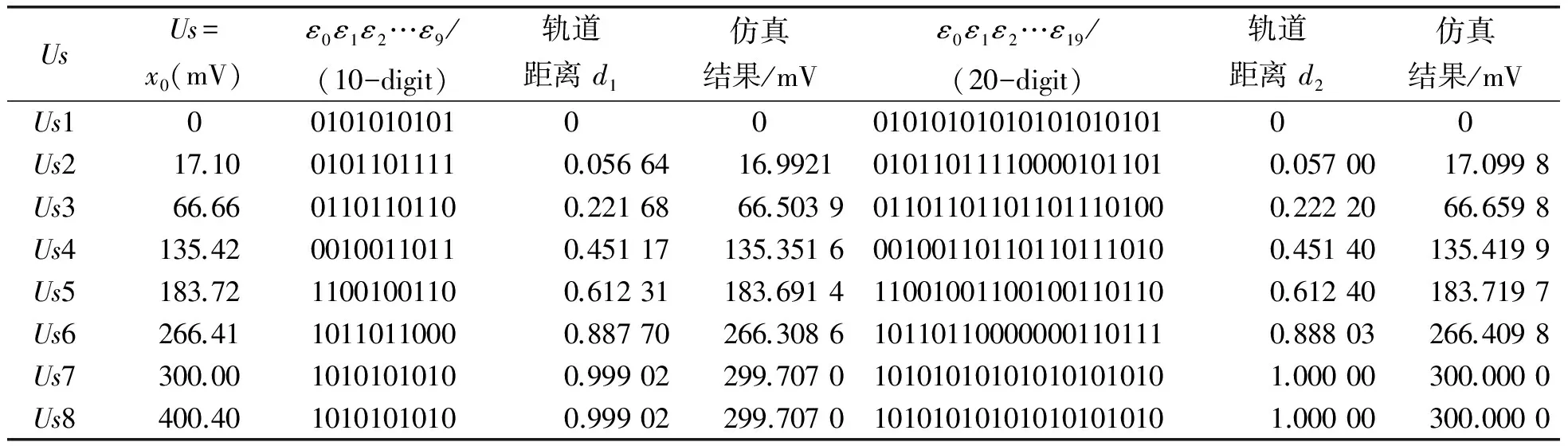
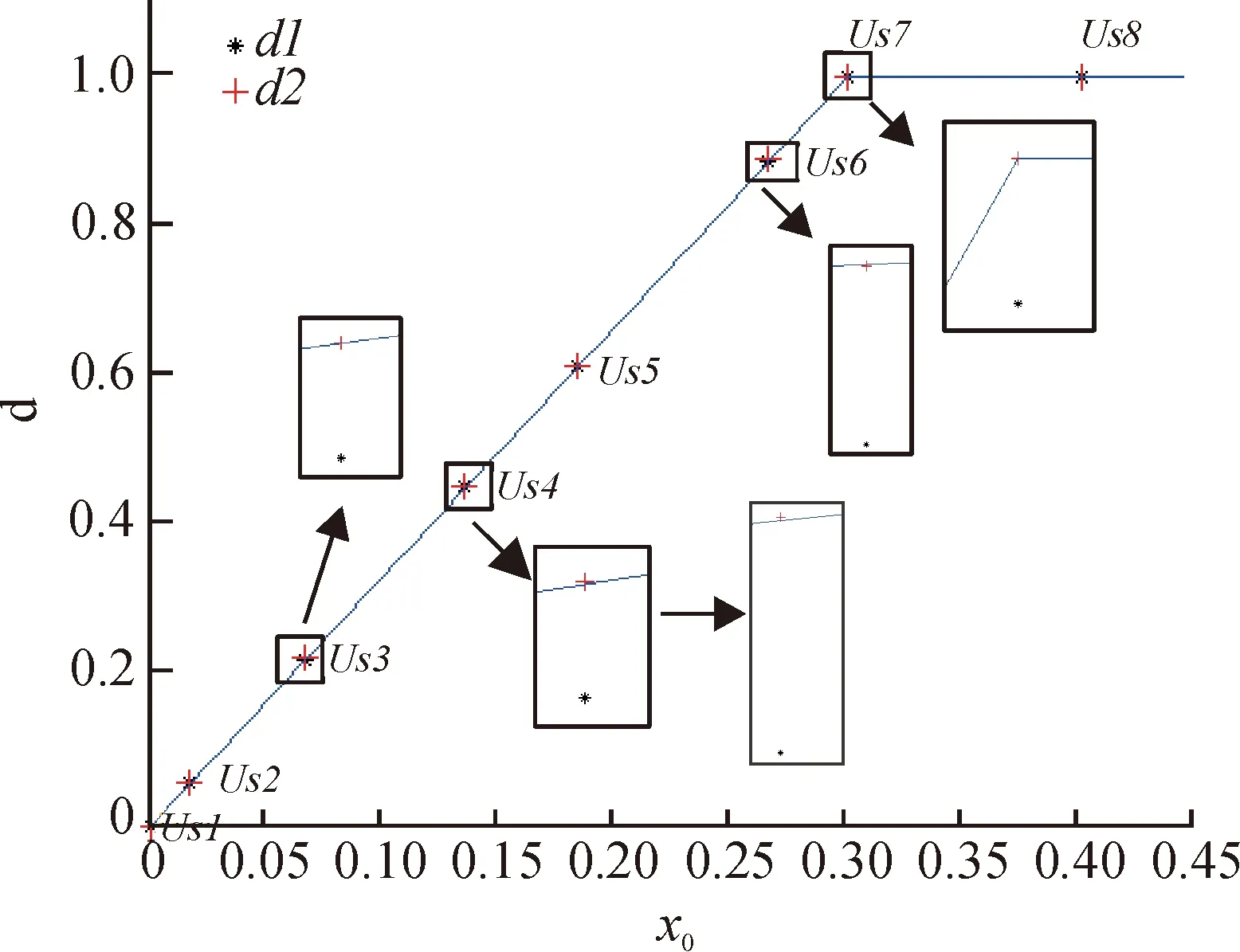
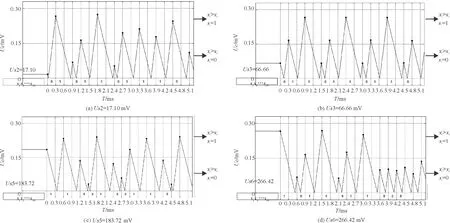
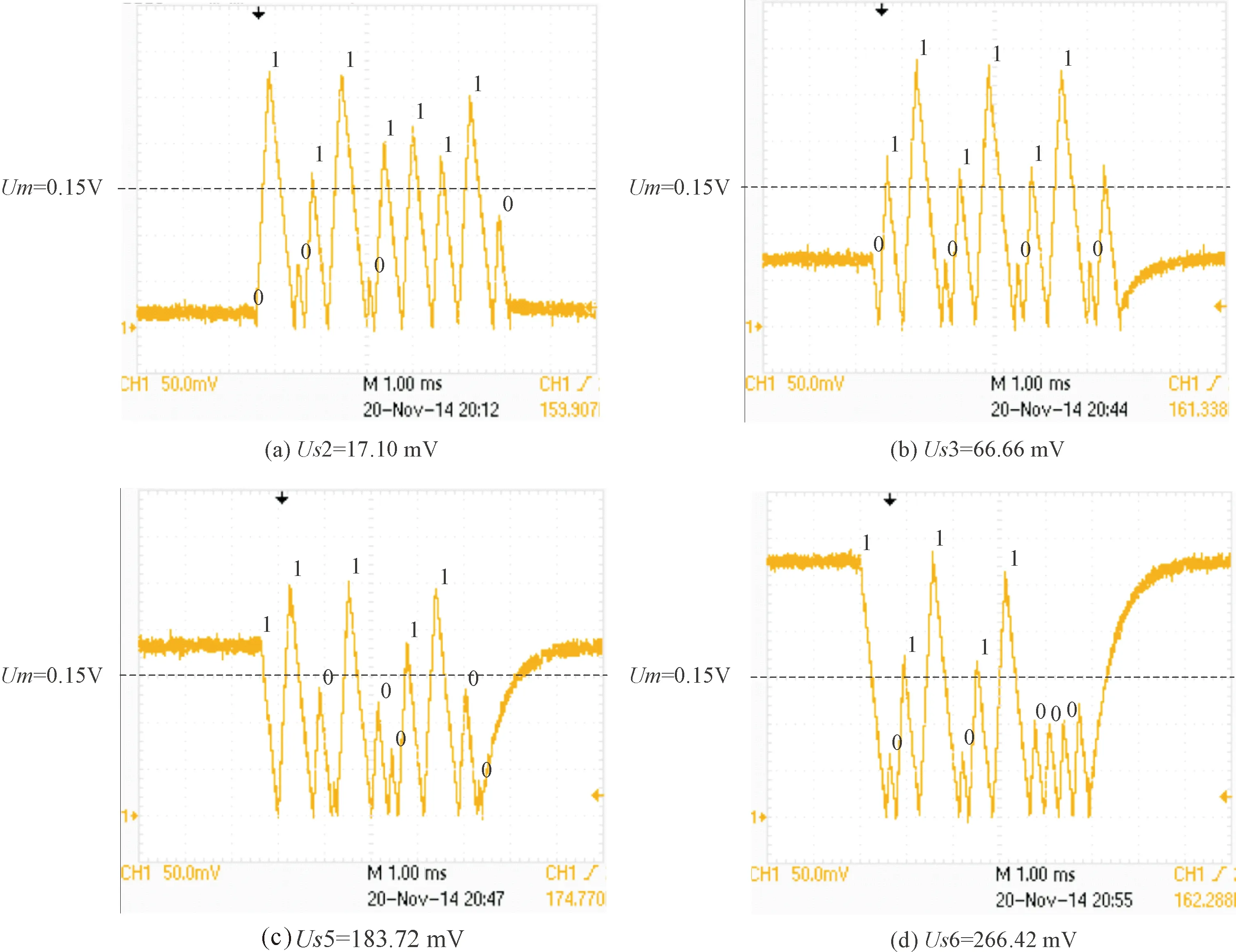
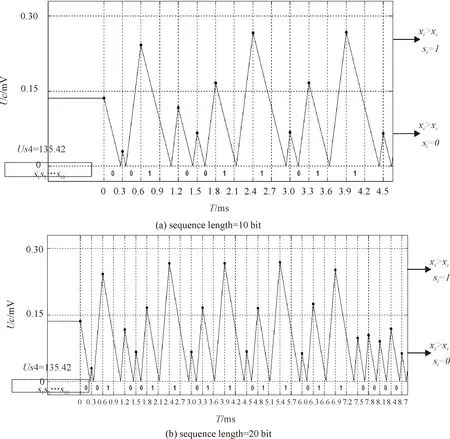
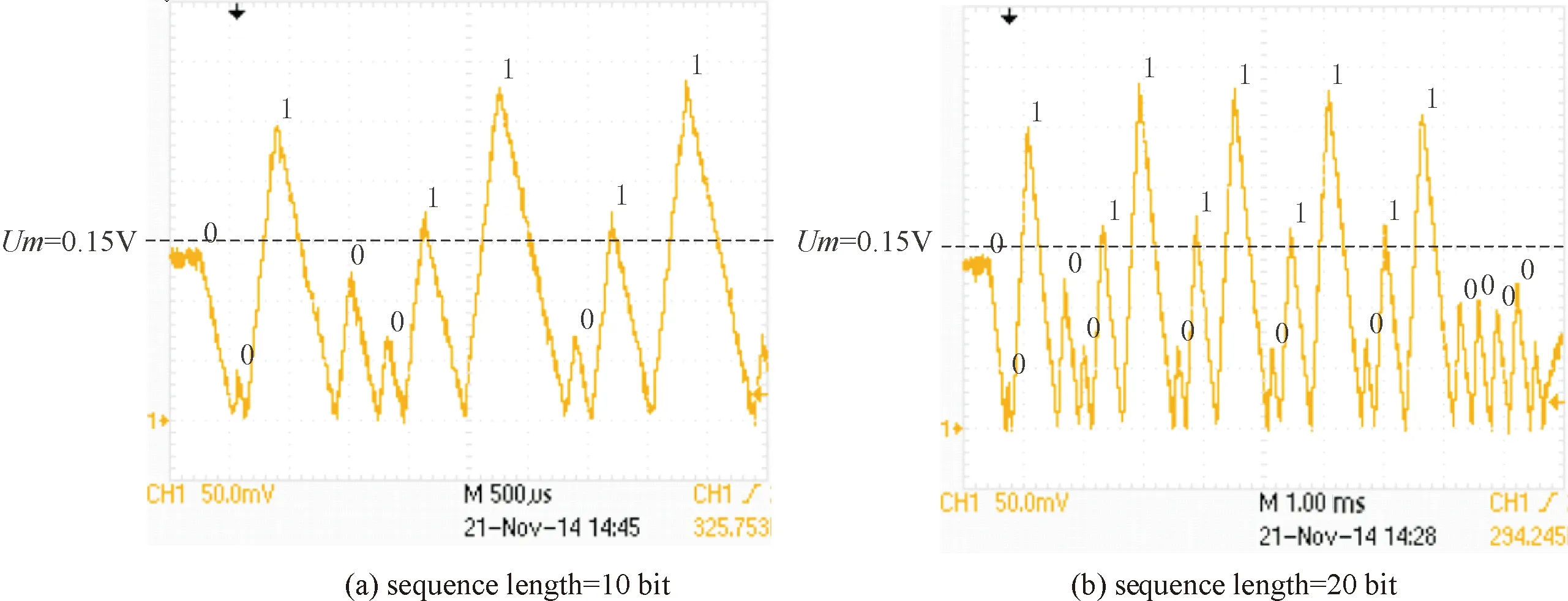
對應的自然序L 符號序列的排序規則為[18] EnL… (8a) OnL…>OnC…>OnR… (8b) 其中,En和(On)分別代表含偶數和奇數個或R或L字母的一串字母.不難看出此排序規則下一切可能的符號序列中最大序列是(RL)∞,而最小序列是(LR)∞;由字母開頭的最靠近C的序列是R(RL)∞,而由字母L開頭的最靠近C的序列是L(LR)∞. 規定符號si的指標εi如下: (9) 則迭代函數(2)可表作 (10) 當k=2時,對上式求逆,可得 (11) 于是,如果x0的符號序列的s0s1s2…sn…不包含C,則上式給出實數x0的如下展開, (12) 現假設x0∈[0,1],y0∈[0,1]為相空間中2個不同初值,經過式(2)迭代分別生成不同的2條軌道x1,x2,x3,…xn,…和y1,y2,y3,…yn,…,它們相對應的符號分別為s0s1s2…sn…,λ0λ1λ2…λn…,定義它們的軌道距離為 (13) 當y0=0即零點時,其符號序列λ0λ1λ2…λn…為010101…或(LR)∞,計算x0和零點之間的距離: (14) 令k=2,將式(13)右邊展開后與等式(14)右側完全相等,因此, d(x0,0)= (15) 為了利用倒鋸齒映射進行測量,在后面的混沌態電路實現中取k=2.這就是說,只要能得到初值x0相對應的符號序列s0s1s2…sn…,就可按式(15)得到軌道距離,再得到x0的值,實現微弱信號的檢測. 4.1 仿真分析 本實驗采用倒鋸齒混沌檢測電路,見圖2,其工作原理:剛開始測量時,斷開開關K1、開關K2,閉合開關K3,待測電壓Us給電容充電,直到電容電壓uc=Us,斷開K3.當有一個周期T的時鐘脈沖到達邏輯電路G時,G控制K2閉合,K1保持斷開,電容以-I2的恒定電流開始放電.當放電結束,即uc=0時,比較器翻轉,Up從高電平降到低電平,G接收到信號,控制開關K2斷開,K1閉合,電容以I1的恒定電流開始充電.當下一個時鐘脈沖到來,邏輯電路G控制K1斷開,K2閉合,電容開始下一個過程的充電.如此重復,Uc的運動軌跡可以得到一條運動軌道. 倒鋸齒混沌檢測電路得到電容充放電的電壓軌道,見圖3. 圖2 倒鋸齒混沌檢測電路 圖3 倒鋸齒映射的運動軌道Fig.3 The motion track of inverted tooth map 根據倒鋸齒混沌檢測電路和圖3可計算出前后時鐘周期電容電壓xn→xn+1的迭代關系式為 (16) 這是一個倒鋸齒映射模型函數. 倒鋸齒映射迭代多次后,根據軌道(2),符號序列(5),定義sn的符號為 (17) 把(17)式帶入(16)式得到: (18) (19) 假設初值x0,y0=0經過倒鋸齒映射后生成的2條軌道對應的符號序列為s0s1s2…sn…,λ0λ1λ2…λn…=010101…,其軌道距離d(x0,0)為 (20) 只要測得x0對應的符號序列就可以求出檢測電路的待測初值Us為 (21) 當取T=0.3 ms,C=2.2 uF,I2=-1.1 mA,I1=2.2 mA時,量程Um=0.3 V,xc=0.15 V,用matlab軟件編程對系統進行數值仿真.可得到電容兩端的混沌態電路和符號序列測量結果如下: 電路參數保持不變,表1的待測初值信號Us與軌道距離d的線性關系,見圖4. 從圖4可見,待測初值與實測值是相同的,待測初值Us在區間[0,Um]內,Us和符號距離d是接近線性關系,在這個區間測量倒鋸齒映射混沌檢測電路的線性度很高.取得位數越高,線性度越好. 4.2 實驗驗證 圖5是倒鋸齒混沌檢測電路實驗電路圖. 表1 Matlab仿真結果 圖4 待測初值信號Us與軌道距離的線性關系 Fig.4 The linear relationship between the initial valueUsand orbital distance 模擬開關采用高速的電子開關MAX333CPP,比較器采用LM393,電容C取2.2 uF,充電電流I1=2.2 mA,放電電流I2=-1.1 mA,脈沖采用單片機定時的方式設置時鐘周期T=0.3 ms,充放電的邏輯轉換用單片機STC89C51編程實現.倒鋸齒映射的數值仿真軌道和實驗軌道,見圖6~9. 從圖6~9可見,電路實驗結果和仿真結果高度接近,電路實驗得到的符號序列和利用公式(21)計算得到的實驗結果見表2.對比表1和表2,實驗結果得到的測量值與仿真結果一樣,誤差低于0.1%,而且符號序列位數越高,實驗結果越精確.此外,若取10位符號序列,即N=10,則測量時間t<2*N*T=3 ms, 因此具有一定的時效性. 從測量的結果看,倒鋸齒混沌檢測電路可以實現高精度測量信號初值電壓,同時測量符號序列位數越多,測量的精度越高.當符號長度為10位時,實驗誤差的計算公式如下: δ=1/210<0.1% (22) 由表2也可觀察實驗的誤差在0.1%以內. 與AD轉換相比,若在取相同數字信號位數N的前提下,倒鋸齒混沌檢測電路可具有更高的分辨率.設定倒鋸齒混沌檢測電路各個參數使檢測滿量程為0.3 V時,倒鋸齒混沌檢測電路的分辨率為0.3 V×(1/28)≈1.17 mV,而AD轉換芯片量程都是5 V.因此,AD轉換芯片的分辨率為5 V×(1/28)≈19.5 mV.倒鋸齒混沌 圖5 實驗電路圖Fig.5 The experimental circuit diagram 圖6 混沌軌道仿真圖Fig.6 Simulation chaos orbits 圖7 混沌軌道實驗圖Fig.7 Experimental chaos orbits 圖8 初始值為Us4=135.42 mV時的混沌軌道仿真圖Fig.8 Simulation chaos orbits at Us4=135.42 mV 圖9 初始值為Us4=135.42 mV時的混沌軌道實驗圖Fig.9 Experimental chaos orbits at Us4=135.42 mV UsUs/mVε0ε1ε2…ε9實驗結果/mVUsUs/mVε0ε1ε2…ε19實驗結果/mVUs117.10010110111116.9921Us266.66011011011066.5039Us3183.721100100110183.6914Us4266.411011011000266.3086Us5135.420010011011135.3516Us5135.4200100110110110111010135.4199 檢測電路的分辨率由取的符號序列位數跟量程共同確定;AD轉換的分辨率只能通過選取不同數字信號位數的芯片來改變其分辨率.根據式(15),倒鋸齒混沌檢測電路可以通過改變放電電流I2、時鐘脈沖周期T和電容大小C來改變測量量程的大小;倒鋸齒混沌檢測電路可以通過取不同位數的符號序列來改變測量分辨率,如取7位、10位或20位等,而AD轉換卻不能,AD轉換只可以選定芯片固定的8的位數的數字信號,如8位和16位等,可以說在選定AD轉換芯片時,其分辨率已經是確定的.因此,倒鋸齒混沌檢測在輸出的數字信號位數相同時,不僅比AD轉換的分辨率要高很多,而且可以更靈活的使用,可根據測量信號的要求改變測量分辨率.尤其在用于檢測微弱信號時,比傳統AD轉換的檢測精度高,倒鋸齒混沌檢測的不足之處是轉換速度沒有AD快.因此,倒鋸齒混沌檢測電路主要用于微弱信號檢測. 本文基于符號動力學的內容,對倒鋸齒映射混沌檢測機理進行分析,揭示了倒鋸齒映射模型應用在微弱信號檢測的本質.數值仿真證明倒鋸齒映射模型在混沌微弱信號檢測中能實現高精度的測量,實驗證明了倒鋸齒映射模型在混沌微弱信號檢測的可行性.符號動力學的優越性,與傳統AD轉換相比位數更多,有更高、更靈活的測量分辨率. [1] HAYASHI M, NAGASAKA K.Wind speed prediction and determination of wind power output with multi-area weather data by Deterministic Chaos[C]∥Proceedings of the 2014 International Conference on Advanced Mechatronic Systems, 2014:192-197. [2] SLUTZKY M W, CVITANOVIC P, MOGUL D J.Manipulating epileptiform bursting in the rat hippocampus using Chaos control and adaptive techniques[J].IEEE Transact Biomed Eng, 2003, 50(5): 559-570. [3] HE L H, JIA M M, DONG Z W, et al.Chaos control for the boost converter under current-mode control[C]∥Chinese Control and Decision Conference Xuzhou, 2010: 3579-3583. [4] ZHENG Y B, DING Q. A new digital chaotic sequence generator based on logistic map[C]∥Proceedings of the 2nd International Conference on Innovations in Bio-inspired Computing and Applications (IBICA), Shenzhan, 2011: 175-178. [5] LORENZ E N.The essence of chaos[M].Washington: The University of Washington Press, 1993:25. [6] JESSA M. Designing security for number sequences generated by means of the sawtooth chaotic map[J]. IEEE Trans Circuits I, 2006, 53: 1140-1150. [7] MA X M, ZHANG B T. Weak signal detecting of gas concentration based on duffing chaotic oscillator[C]∥Proceedings of the 2010 International Conference on Computer Application and System Modeling (ICCASM), Taiyuan, 2010, VI-183-VI-186. [8] NIE C Y, WANG Z W.Application of chaos in weak signal detection[C]∥Proceedings of the 2011 Third International Conference on Measuring Technology and Mechatronics Automation,2011:528-531. [9] LIU X C, LIU X L.Weak signal detection study based on duffing chaos circuit used for downhole communication[C]∥Proceedings of the 2010 2nd International Symposium on Information Engineering and Electronic Commerce,2010:1-4. [10]HU W J, LIU Z Z. Study of metal detection based on chaotic theory[C]∥Proceedings of the 8th World Congress on Intelligent Control and Automation, Jinan, 2010: 2309-2314. [11]GAO B K, ZHANG C, YANG F, et al. High accuracy chaotic oscillators ultrasonic wave liquid level detection[C]∥Proceedings of the 2012 International Conference on Measurement, Information and Control (MIC), Harbin, 2012: 735-739. [12]ZHANG Y Q, MA X M, GONG X F. Fault diagnosis method of mining mechanism equipment based on chaotic Duffing Oscillator (in Chinese)[J]. Coal Min Mach, 2014, 35: 0276-0279. [13]XU Y C, QU X D, YAN C L. The study of novel chaotic oscillator detecting weak signal amplitude[C]∥Proceedings of the 7th IEEE Conference on Industrial Electronics and Applications (ICIEA), Singapore, 2012: 303-307. [14]DA C J, MU S, MA D S, et al. The theoretical study of the turning period in numerical weather prediction models based on the Lorenz equations (in Chinese)[J]. Acta Phys Sin, 2014, 63: 029201-1-029201-14. [15]LING Q W, CHEN Y Q. Study of weak signal’s direct digital measurement based on chaos (in Chinese)[J]. Chin J Sens Act, 2006, 19: 443-446. [16] 郝柏林.從拋物線談起——混沌動力學引論[M].2版.北京:北京大學出版社, 2013: 38-44. HAO B L. From a parabolic——An introduction to chaos dynamics[M]. 2nd Ed. Beijing:Peking University Press, 2013:38-44. [17]鄭偉謀, 郝柏林.實用符號動力學[M].上海:上海科技教育出版社, 1994: 11-86. ZHENG W M, HAO B L. Practical symbolic dynamics[M]. Shanghai: Shanghai Science and Technology Press, 1994:11-86. [18]郝柏林. 實用符號動力學與混沌[M]. 2版(英文版). 北京: 北京大學出版社, 2014. HAO B L. Applied symbolic dynamics and chaos[M]. 2nd Ed(in English). Beijing: Beijing University Press, 2014. 【責任編輯: 陳 鋼】 The chaos detection mechanism of inverted sawtooth map based on symbolic dynamics YANG Ru, WANG Yan-fen, FENG Jin-peng (School of Physics and Electronic Engineering, Guangzhou University, Guangzhou 510006, China) Based on the sensibility of the parameter and the initial value of chaotic system, the proposed method begins from inverted saw-tooth map and builds the symbolic sequence space according to symbolic dynamics. The measured value can be calculated by the space distance of two tracks including the initial value and the zero point. The constant current source is used to charge and discharge the capacitor, and the analysis and design of the chaotic detection circuit is applied to detect the weak signal. inverted saw-tooth map; symbolic dynamics; weak signal detection 2016-07-18; 2016-09-28 國家自然科學基金資助項目(51277035);廣東省自然科學基金資助項目(2014A030313528) 楊 汝(1971-),女,教授,博士.E-mail:yangru@gzhu.edu.cn 1671- 4229(2016)06-0039-08 TN 911.233 符號序列的軌道距離
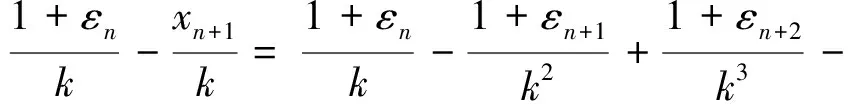
4 倒鋸齒映射混沌檢測分析和實驗
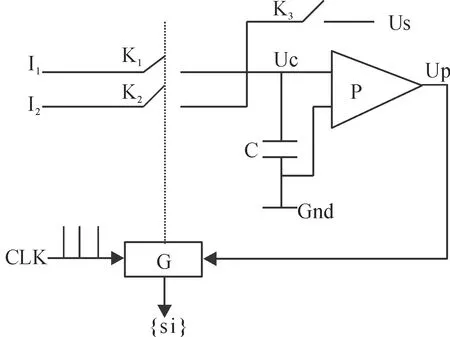
Fig.2 The chaotic detection circuit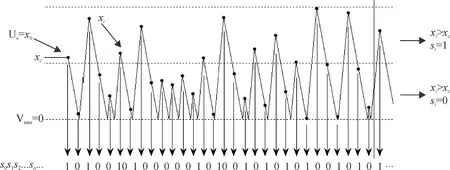
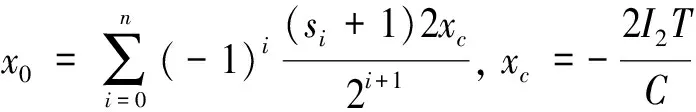
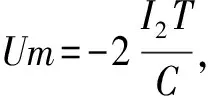


5 結 論

