基于模型預測控制方法的發動機低耗油率控制

楊 蓓，吳 瓊（南昌航空大學飛行器動力工程學院，江西南昌330063）

基于模型預測控制方法的發動機低耗油率控制

楊 蓓，吳 瓊（南昌航空大學飛行器動力工程學院，江西南昌330063）

模型預測控制是一種不同于經典控制方法的控制策略，該方法通過將控制問題轉化為針對目標函數的優化問題來計算控制規律、達到降低燃油消耗的控制目標。模型預測控制可以經由加權矩陣的選取以達到特定的控制目標，通過將燃油消耗作為控制目標函數，可以降低燃油的消耗量。

模型預測控制；航空發動機；非線性模型；離散模型

1 引言

航空發動機工作過程復雜，工作狀態的變化較大，必須對其加以控制以確保其穩定、可靠地運行，并降低其燃油消耗、提高經濟效益[1]。經典反饋控制理論已經很難達到降低燃油消耗的需求[2]。模型預測控制（Model Predictive Control，MPC）是被廣泛討論的一種反饋控制策略。在每一采樣時刻，根據獲得的當前測量信息，求解優化問題，并將獲得的第一個控制序列的元素作用于發動機，并在一直重復該過程。在線求解開環優化問題獲得優化序列是MPC與傳統控制的主要區別。MPC可在選取控制規律時便明確考慮燃油消耗這等約束[2，3]。

MPC不根據當前和過去的偏差來產生控制作用，而是評估應用各種備選控制輸入序列所能帶來的結果，并從中選取使性能度量最小化的控制序列。在合理選擇性能指標中的加權矩陣的基礎上，MPC可以在很大程度上實現燃油消耗量的最優控制，并可針對非線性模型進行控制。但MPC解決優化問題所需的計算量過大。必須計算密集的約束優化問題[2，4，5]，以為確保發動機不過分偏離預測初始值，快速完成預測和確定最優控制序列。

2 模型預測控制與控制器設計

在進行的發動機控制系統設計時，采用部件級模型[6]。部件級模型是基于組成發動機的各個部件的模型建立起來部件級模型建模過程中所需的數據將從GSP軟件中獲取[7]。

發動機動態過程模型中需要考慮轉子的慣性，從而獲得轉子功率平衡方程式，建立部件級模型。再通過線性化來獲得線性模型以降低計算量。

通過狀態空間模型建立預測控制的基本原理和算法是一種較好的選擇。按照預測控制的基本原理可以分為三個步驟：①預測系統未來動態；②求解優化問題；③將解的第一個元素作用于系統。并根據參考指令和測量值不斷重復執行這些操作[3]。

根據線性化可以得到連續時間狀態方程。采用離散模型在推導上有許多便利，因此將線性系統轉為離散的狀態空間表達式（1）：

式中：x（k）∈Rnx是狀態變量；u（k）∈Rnu是控制輸入變量；yc（k）∈Rnc是被控輸出變量。

基于離散狀態方程模型預測系統未來動態是模型預測控制的第一步。將上述離散方程改寫為增量式可得：

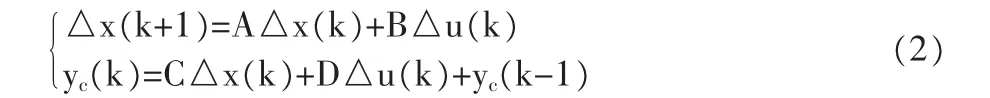
式中：△x（k）=x（k）-x（k-1），△u（k）=u（k）-u（k-1）。

根據預測控制的原理，需要先以最新測量值為初始條件，基于模型（2）預測系統未來動態。設定預測時域為p，控制時域m，且m≤p。在k時刻，測量值為x（k），計算△x（k）=x（k）-x（k-1），并將△x（k）作為預測系統未來動態的初始條件。在獲得了x（k）之后，可以根據公式（2）預測k+1及以后的狀態增量：

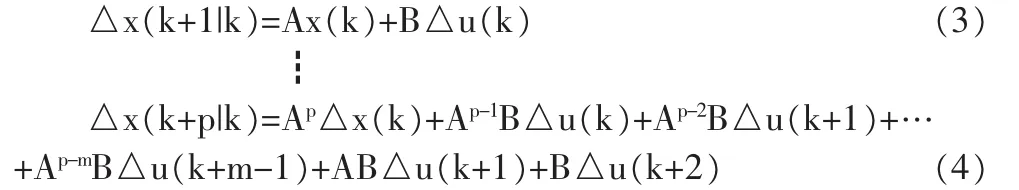
進一步，根據公式（2）～（4）預測系統在k+1到k+p的輸出值yc：

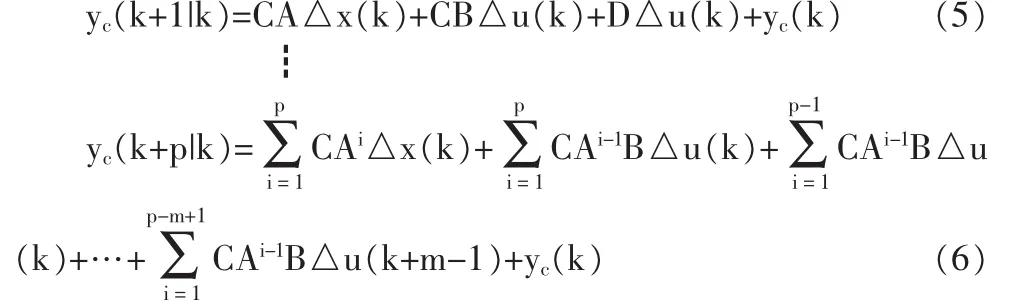
為方便后續公式推導，先定義p步預測輸出向量Yp（k+1| k）和m步輸入向量△U（k）。對于多輸入多輸出系統，yc（k+i|k）∈Rn×1，△u（k+i）∈Rn×1，即p×1表示矩陣Yp（k+1|k）中輸出的個數，而非矩陣Yp（k+1|k）的維數。

總結式（2）～（6）可得：

k+1時刻的輸入對k及之前時刻的輸出沒有影響，但會對k+1之后的輸出有作用[3]。

在選擇目標函數時，該目標函數應能夠表現對降低燃油消耗這一需求，可以將目標函數選擇為：

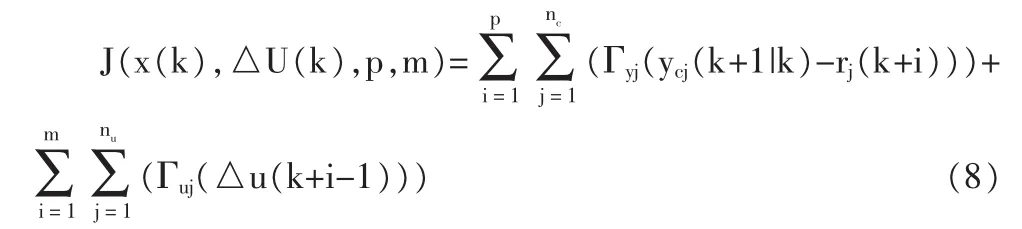
式中：rJ（k+i），i=1，2，…，p位給定的參考輸入序列的第j個分量；Γyj是對第j個預測控制輸出誤差的加權因子。加權因子大則對系統輸出偏差的要求越小。可以將（9）寫成范數形式：

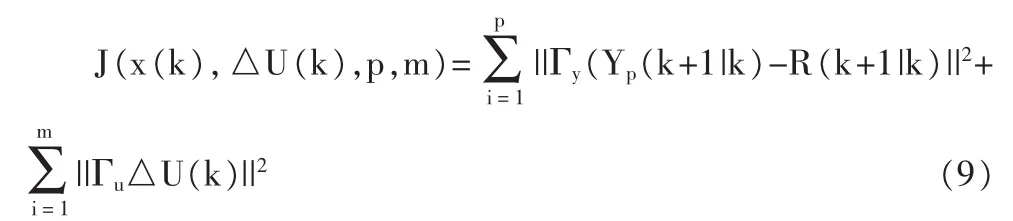
控制加權因子Γu，i越大，表明期望的控制動作變化越小。

最終可以將優化問題歸結為：

min△U（k）J（x（k），△U（k），p，m）

將目標函數（9）寫為矩陣向量形式，可得：

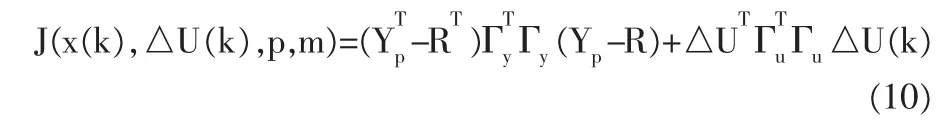
參考輸入序列為：

定義Ep（k+1|k）可得：

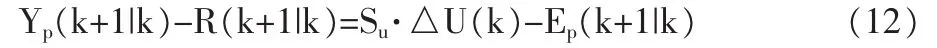
聯立式（11）（12）最終可得：

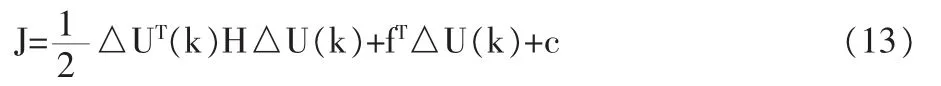
式中：c是綜合而來的常數。

對式（13）進行最優化計算即可得：

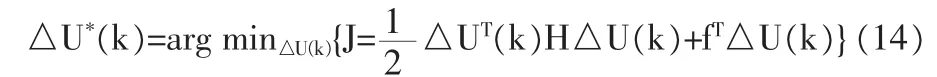
在完成預測控制的第二步之后，執行第三個步驟，將開環最優控制序列的第一個元素作用于系統。

3 系統仿真示例

當某發動機在飛行高度H=10km、Ma=0.9、低壓轉子轉速nL=96%時的工作狀態，可以獲得其系統的線性化方程[9]：

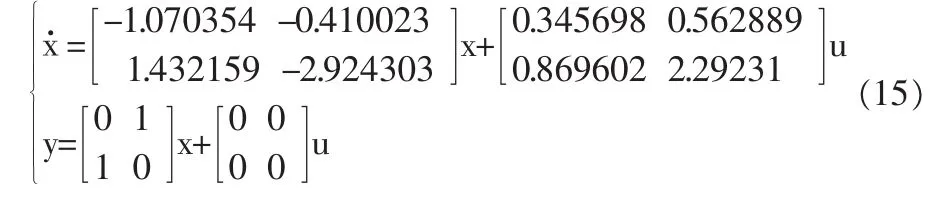
選擇狀態為x=[nHnL]T；輸入為u=[qm，fA8]T，分別為供油量和尾噴口面積。選擇系統輸出和輸入加權矩陣為（16）所示的對角陣，并選擇預測步長為10，控制步長為8。

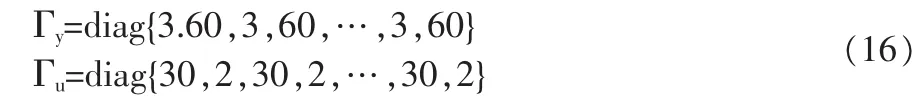
仿真結果如圖1～2所示。所選的參考指令如圖中虛線所示，低壓轉子轉速跟蹤效果較好，高壓轉子轉速基本無變化，如圖2可知，燃油流量有了明顯的降低。

由圖可知，發動機低壓轉子轉速nL較好地跟上了指令信號，燃油流量有了明顯下降。可以通過修改輸出加權矩陣對系統輸出量進行調整。

4 結論

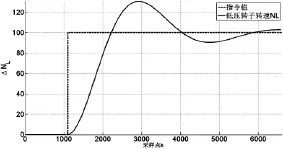
圖1 nL跟蹤指令信號

圖2 燃油流量變化

通過選定特定控制目標，并求解二次優化問題可以較好地解決MIMO問題。使用模型預測控制，跟經典的PID控制器相比，可以有效降低燃油消耗，提高民用航空產業的經濟效益。

[1]樊思齊.航空發動機控制[M].西安：西北工業大學出版社，2008.

[2]Richter Hanz.Advanced Control of Turbofan Engines[M].Springer Science&Business Media，2011.

[3]陳 虹.模型預測控制[M].北京：科學出版社，2013.

[4]Brunell B J，Bitmead R R，Connolly A J.Nonlinear Model Predictive Control of an Aircraft Gas Turbine Engine[C].IEEE CONFERENCE ON DECISION AND CONTROL.2002：4649～4651 vol.4.

[5]Richter H，Singaraju A V，Litt J S.Multiplexed Predictive Control of a Large Commercial Turbofan Engine[J].Journal of Guidance Control&Dyna mics，2008，31（2）：273～281.

[6]孫健國，李秋紅，楊 剛.航空燃氣渦輪發動機控制[M].上海：上海交通大學出版社，2014.

[7]夏 超，王繼強，商國軍，等.基于Matlab/Simulink的航空發動機部件級建模與分析[J].航空發動機，2012，38（04）：31～33.

[8]鄒 濤，丁寶蒼，張 端.模型預測控制工程應用導論[M].化學工業出版社，2010.

[9]吳志琨.渦扇發動機控制系統設計研究[D].西北工業大學，2007.

TK321

A

2095-2066（2016）36-0004-02

2016-12-13

楊蓓（1979-），女，講師，研究方向為航空發動機控制。