提高MMC高效電磁暫態模型仿真精度的方法

郭琦，王嘉鈺，林雪華，李巖，劉崇茹

(1.南方電網科學研究院，廣州市 510080；2.華北電力大學電氣與電子工程學院，北京市 102206)

提高MMC高效電磁暫態模型仿真精度的方法

郭琦1，王嘉鈺2，林雪華1，李巖1，劉崇茹2

(1.南方電網科學研究院，廣州市 510080；2.華北電力大學電氣與電子工程學院，北京市 102206)

對基于戴維南等效原理的模塊化多電平換流器(modular multilevel converter, MMC)橋臂電磁暫態仿真詳細模型的數學原理進行了分析，發現當仿真過程中發生故障或開關動作等引起網絡結構變化時，由于電容電流會發生突變，當采用梯形積分法計算時會引入計算誤差。為了解決這一問題，提出了一種通過求解突變后的非狀態變量來消除計算誤差的方法，在PSCAD/EMTDC下對比分析了誤差消除前后在開關變化時刻的電容電壓，驗證了本方法的正確性和有效性。同時，搭建了單端101電平MMC-HVDC仿真系統，驗證了本文提出的改進計算模型的正確性。

模塊化多電平換流器(MMC)；戴維南等效；梯形積分法；計算誤差；仿真精度

0 引 言

隨著電力電子器件和控制技術的發展，基于電壓源換流器的高壓直流輸電(voltage source converter based on HVDC, VSC-HVDC)技術得到了越來越廣泛的應用[1-3]。其中，模塊化多電平換流器(modular multilevel converter, MMC)與兩電平、三電平換流器相比，具有制造難度更低、開關損耗更少、階躍電壓更低、波形質量更高、故障處理更強等優勢[4]，成為VSC-HVDC的發展趨勢。

文獻[5]首次提出基于戴維南等效原理的MMC模型，為MMC電磁暫態離線等效模型和實時仿真模型研究奠定了堅實的理論基礎。文獻[6]提出了一種基于節點電壓法的仿真方法，該方法將原有的MMC等值網絡矩陣分割成若干個小矩陣，以此減少等值網絡矩陣計算維度，提升了仿真速度，但這種方法造成了子模塊與主網絡之間相差1個步長的仿真時間。文獻[7]提出了一種快速同步解決方案，通過諾頓等效將原有的橋臂等值為2節點等值電路輸出給等值網絡矩陣，但該文獻對電容采用了梯形積分法，如不加處理會出現梯形積分的計算誤差問題。為此，文獻[8]采用了后退歐拉法來避免誤差，但犧牲了仿真精度。

為了有效地解決在電磁暫態仿真中采用梯形積分計算MMC仿真模型帶來的誤差問題，本文通過分析電磁暫態仿真中采用梯形積計算產生誤差的原因，提出一種消除MMC橋臂詳細等效模型采用梯形積分算法帶來誤差的方法，提高MMC橋臂詳細等效模型的精度。

1 MMC的拓撲結構及工作原理

三相MMC的拓撲結構如圖1所示，O點表示零電位參考點。一個換流器由6個橋臂(arm)構成，其中每個橋臂由N個結構相同的子模塊(sub-module，SM)與一個電抗器L串聯構成，上下兩個橋臂構成一個相單元(phase unit)[9]。MMC正常工作時，每相上、下橋臂各有N個子模塊配合投切，任意時刻保持同時投入的子模塊總數為N，可維持直流電壓Udc恒定。

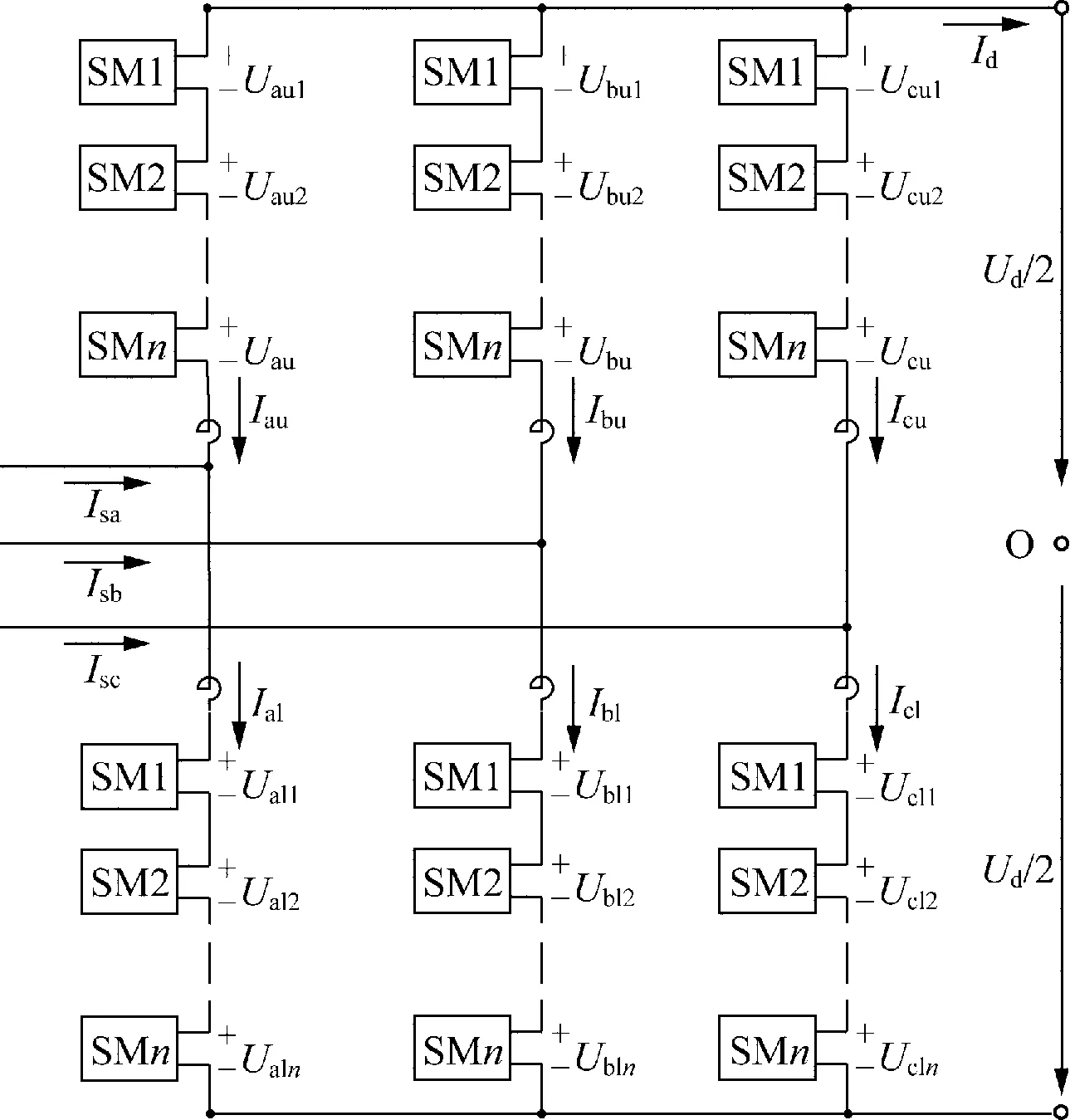
圖1 MMC拓撲結構Fig.1 Topology of MMC

圖2為 MMC 中常采用的半橋結構子模塊(half-bridge SM，HBSM)，每個子模塊主要由2個絕緣柵雙極型晶體管(insulated gate bipolar transistor，IGBT)開關(T1和T2)，2個反并聯二極管(D1和D2)以及直流儲能電容(C)組成。其中Iarm、Usm和UC分別為橋臂電流、子模塊端口電壓和電容電壓。在正常運行時，T1和T2不同時導通。當T1導通時，子模塊輸出電壓為UC；當T2導通時，子模塊輸出電壓為0。

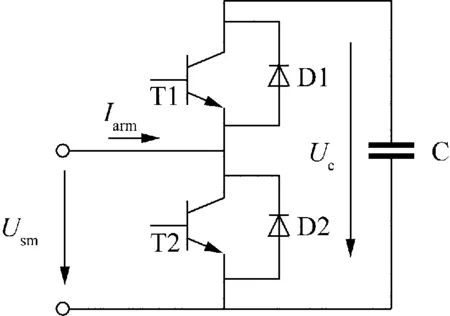
圖2 子模塊拓撲結構Fig.2 Topology of sub-module

2 MMC詳細等效模型

MMC橋臂的戴維南等效模型是基于建立單個子模塊的戴維南等效電路并進行代數疊加而實現的，從而將每個MMC橋臂等效為一個電壓源與電阻串聯的 2節點支路，根據相應的電氣關系更新該橋臂中各子模塊的電容電壓[10-11]。

本文基于戴維南等效原理，建立了MMC詳細等效模型，建模過程見圖3。

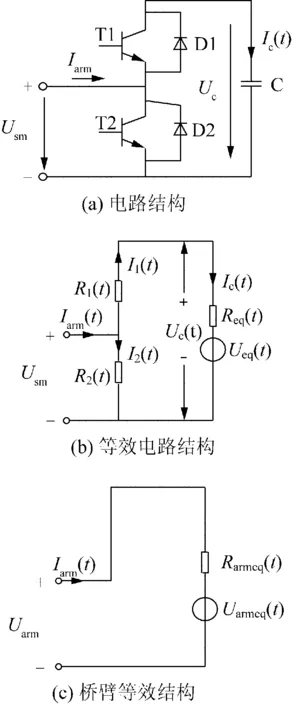
圖3 MMC子模塊Fig.3 MMC sub-module

(1)首先將圖3(a)中的開關元件T1和T2和反并聯二極管D1和D2構成的兩組開關組(上開關組由T1和D1反并聯構成，下開關組由T2和D2反并聯構成)，分別用可變電阻R1、R2表示導通/關斷兩種狀態。T1導通，T2關斷時，R1為一相當小的值，R2為一相當大的值；當T1關斷，T2導通時，R1為一相當大的值，R2為一相當小的值。

(2)如圖3(b)所示，電容的電壓電流關系為

(1)

采用梯形積分對電容進行離散化：

(2)

式中：Uc(t)、Uc(t-Δt)分別為當前時刻和前一時刻的電容電壓；Ic(t)、Ic(t-Δt)分別為當前時刻和前一時刻的電容電流；C為子模塊電容值；t為電磁暫態仿真時間；Δt為電磁暫態仿真步長。

由(2)式可知，任意時刻電容電壓和電流的關系。因此，每個子模塊電容可以等效為戴維南電阻Req(t)和戴維南等值電壓Ueq(t)：

(3)

(4)

(3)如圖3(c)所示，結合可變電阻R1(t)、R2(t)求取單個子模塊的戴維南等效電阻Rsmeq(t)與戴維南等值電壓Usmeq(t)：

(5)

(6)

并基于此將MMC橋臂上N個串聯的子模塊的戴維南電路進行疊加，得到橋臂的等值電阻Rarmeq(t)和等值電壓Uarmeq(t)：

(7)

(8)

(4)最后根據以上MMC詳細等效模型建模過程，計算子模塊電容電流和電容電壓：

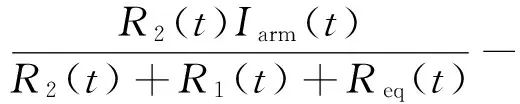
(9)

Uc(t)=Ueq(t)+Ic(t)Req(t)

(10)

式中Iarm(t)為橋臂電流。

3 提高MMC高效電磁暫態仿真精度的方法

3.1 電磁暫態計算的數值方法

采用數值方法計算電磁暫態過程，常見的做法是將微分方程差分化來計算某一時刻的狀態。差分方程可以由純電阻和電壓源構成的電路來代替，以反映t時刻未知電壓和電流之間的關系。其中電阻值取決于元件的參數和積分步長，電壓源取決于前一時刻的電壓和電流值。這種等值電路稱為暫態等值計算電路[12-14]。

根據各元件之間的實際接線方式，將其暫態等值計算電路進行相應的連接，并對這一網絡進行求解，即可得出每個時刻各個元件的電壓和電流。依次對各個步長進行遞推計算，便可求得整個暫態過程的數值解。

3.2 計算誤差的產生

對于電力系統中的元件，總可以列出描述其暫態過程中電壓和電流間關系的微分方程，然后應用數值方法進行求解。

由于隱式梯形積分比較簡單而且具有相當高的精度和良好的數值穩定性，并能較好地適應剛性微分方程組，因此在電磁暫態仿真程序(electro-magnetic transients program, EMTP)計算中通常都采用這種方法。但當仿真過程中出現故障或者開關動作等引起網絡結構突變時，采用隱式梯形積分法無法獲取正確的非狀態變量，從而會產生計算誤差[15]。

采用梯形積分法的子模塊等效模型如圖3(b)所示，設兩個相鄰計算時刻為t1和t2，且有t2=t1+Δt，則有：

(11)

式中：Uc(t1)和Uc(t2)分別為相鄰t1、t2時刻子模塊的電容電壓；Ic(t1)和Ic(t2)分別為相鄰t1、t2時刻流經子模塊電容的電流。

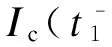
(12)

而實際正確的電磁暫態仿真過程計算應該采用式(13)：

(13)

3.3 提高仿真精度的方法

在仿真過程中當發生故障或者開關動作等引起網絡結構突變時，采用式(12)的常用梯形積分方法進行計算，會引起比較大的計算誤差。這是因為網絡中故障時刻的非狀態變量發生了突變，在修改網絡的導納矩陣后，仍以突變前的電量計算下一時刻的等值注入電源，會導致計算結果不正確。因此，為了得到正確的突變后的值而能夠采用式(13)進行計算，本文提出了求解突變后的非狀態變量的方法，從而消除由梯形積分表達式中的邊界參數突變而產生的計算誤差，等效橋臂模型修正計算方法流程如圖4所示。

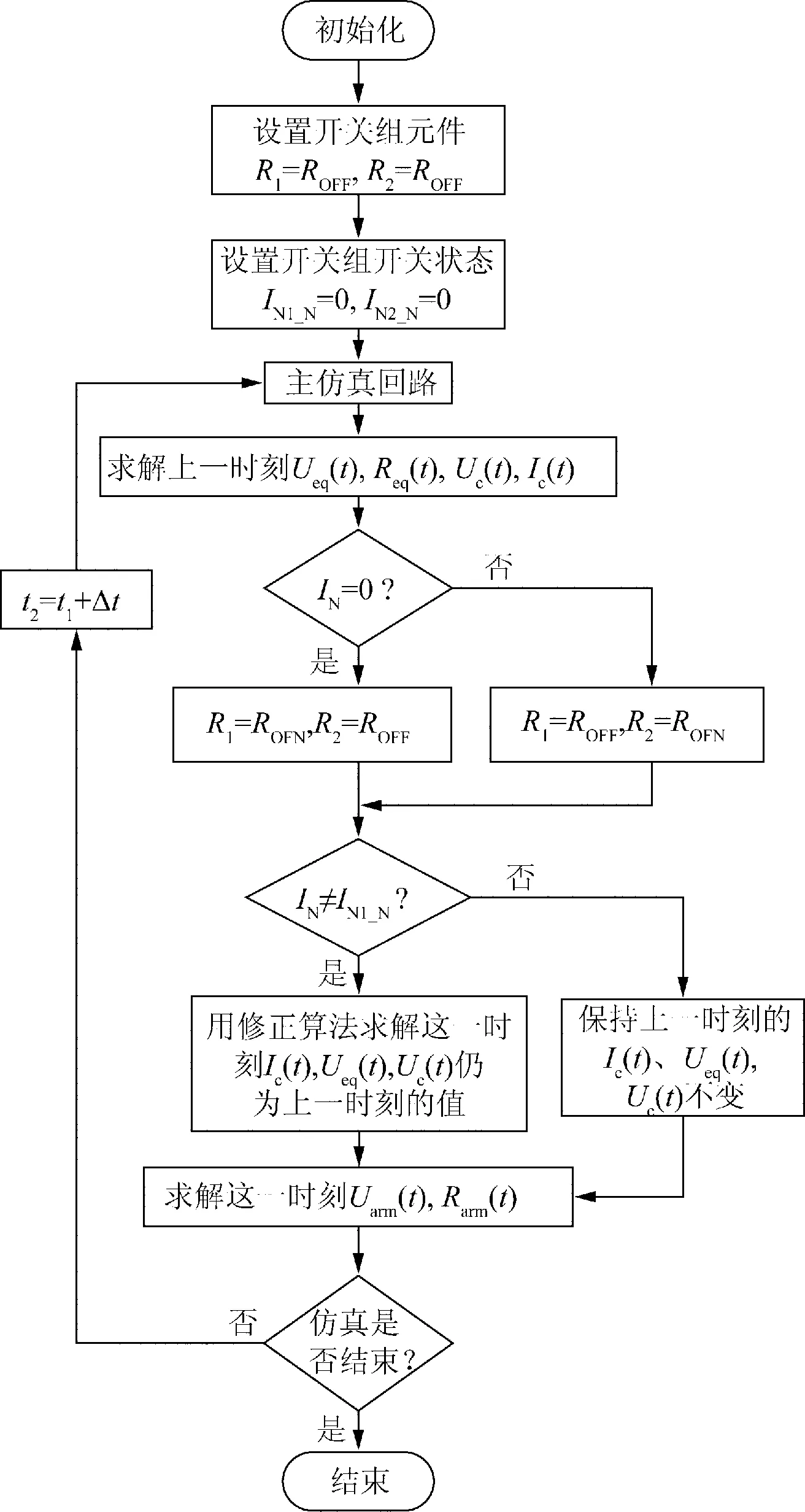
圖4 等效橋臂模型修正計算方法流程圖Fig.4 Flow chat of improved calculation method for equivalent arm model

圖中，RON、ROFF分別表示可變小、大電阻；IN1_N、IN2_N表示單子模塊上、下管開關狀態，其中IN1_N=0表示上管導通，IN2_N=0表示下管導通；IN表示當前時刻的上管開關狀態。

具體實現過程如下：

(1)程序初始化；

(2)從T=0開始仿真計算，按照第2節MMC建模過程依次求解Ueq(t)、Req(t)、Ic(t)、Uc(t)；

(3)根據當前時刻上管的開關狀態判斷R1、R2的等效情況；

(4)判斷當前時刻上管的開關狀態是否發生改變，若改變則考慮電容電流突變特性，修正原始等效建模過程中Ic(t)的計算結果；若不改變則保持第(2)步的等效結果不變；

(5)通過修正后的Ic(t)、Ueq(t)求解這一時刻等效橋臂的Uarm(t)、Rarm(t)；

(6)判斷仿真是否結束，若否則返回(2)繼續計算。

根據式(3)、(4)、(10)和(13)，將圖3(b)中的Ic、Ueq、Uc替換為修正后的等效值，則有t1時刻的橋臂電流：

(14)

令：

(15)

式中：Iarm(t1)是t1時刻流經MMC橋臂的橋臂電流；I2(t1)是t1時刻流過子模塊可變電阻R2的電流；Usm(t1)是t1時刻子模塊端口電壓。

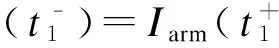
(16)

那么t1時刻等效戴維南電壓Ueq(t1)的修正表達式為

(17)

因此t2時刻的電容電壓等效修正表達式為

(18)

式中Rc是電容等效電阻值。

4 仿真分析

如圖5所示，在PSCAD中采用Frotran語言自定義編寫MMC等效橋臂模型，搭建MMC等效橋臂測試電路，開關組元件用可變電阻R1、R2實現，其中R1=0.005 Ω，R2=106Ω，交流側采用單相電壓源，電壓源內阻為1 Ω，串聯電感為0.1 H，子模塊電容為0.03 F。

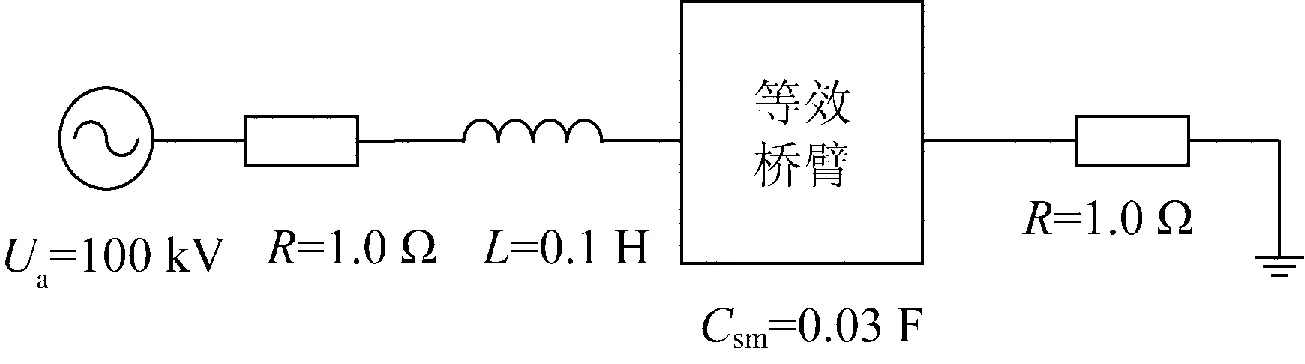
圖5 等效橋臂電路測試示意圖Fig.5 Schematic diagram of circuit test for equivalent arm model

1.49 s時，等效橋臂的開關斷開，電容不再充電。分3種情況進行仿真，觀測電容電流：(1)采用未修正梯形積分邊界條件的戴維南等效橋臂模型；(2)采用修正梯形積分邊界條件后的戴維南等效橋臂模型；(3)采用器件搭建的詳細模型。仿真結果見圖6。

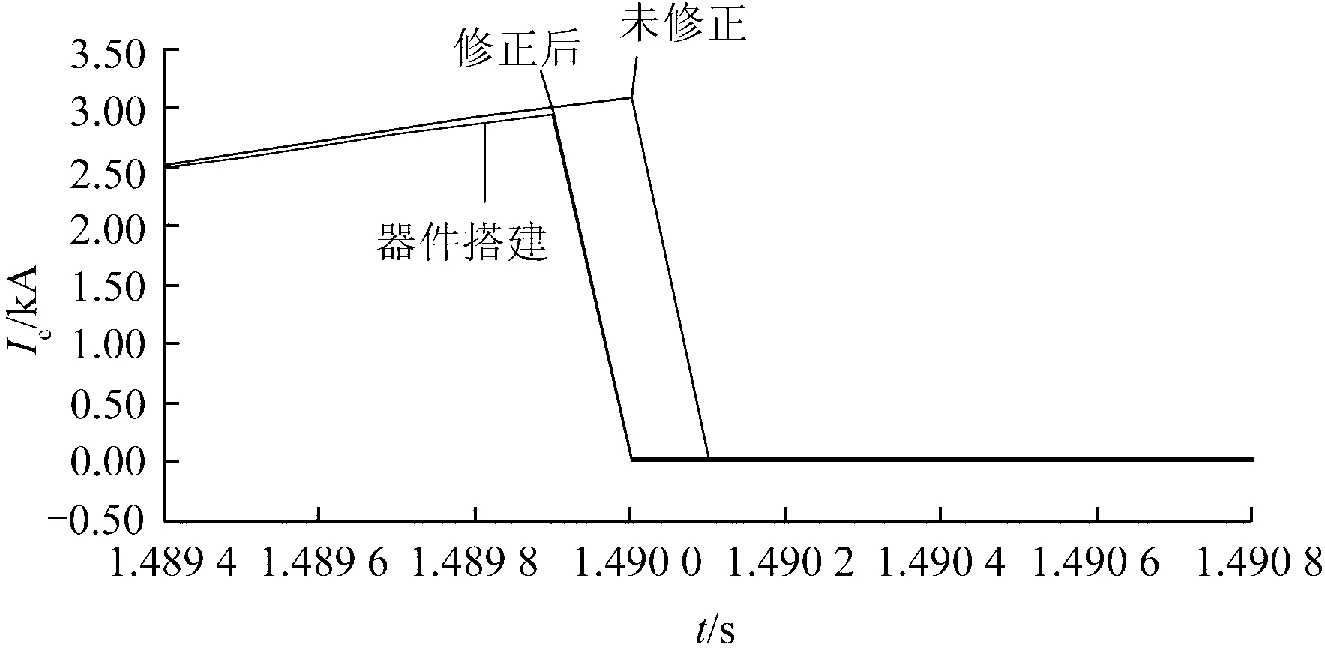
圖6 不同橋臂模型下流過電容的電流Fig.6 Capacitor current in different arm models

可以看出，若橋臂開關狀態未發生改變，不論是修正的橋臂等效模型或是未修正的橋臂等效模型其電容電流與詳細模型的電容電流趨勢基本一致，而在1.49 s時，開關斷開，未修正的橋臂模型其電容電流與詳細模型的電容電流偏差較大，而修正后的橋臂模型其電容電流與詳細模型的電容電流趨勢基本一致。

在1.49 s時分2種情況進行仿真，觀測電容電壓：(1)采用未修正梯形積分邊界條件的戴維南等效橋臂模型；(2)采用修正梯形積分邊界條件后的戴維南等效橋臂模型。仿真結果見圖7。

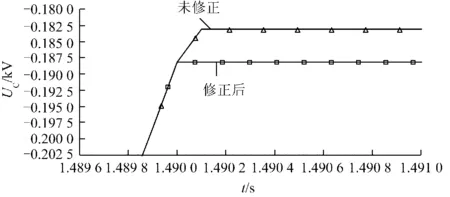
圖7 開關變化前后電容電壓對比Fig.7 Capacitor voltage comparison before and after switch changing

可以看出，采用未修正的橋臂模型的電容電壓繼續升高，一個步長后維持新的定值，由于未修正的橋臂模型未考慮開關狀態變化瞬間電流的突變，由此得到的電容電壓比真實值大；采用修正后的橋臂模型，由于電容電壓在開關狀態改變時刻并不突變，所以其電容電壓仍保持當前時刻的值不變。

單端101電平MMC-HVDC測試系統如圖8所示。

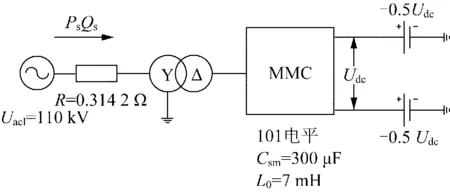
圖8 單端101電平MMC-HVDC系統Fig.8 Single-terminal 101-level MMC-HVDC system

采用兩種戴維南等效橋臂模型在單端101電平MMC-HVDC仿真系統下進行仿真，電容電壓和開關狀態曲線見圖9，當T=1.78 s時，開關狀態從閉合到斷開時，電容從投入狀態切換至旁路狀態。

從圖9(a)中可以看出，開關狀態發生變化后，由于電流沒有被修正，導致電容電壓在開關斷開后還持續放電，這是不正確的。

從圖9(b)可以看出，修正邊界條件后，在仿真計算過程中，開關狀態發生變化后，子模塊電容電壓在下一計算時刻就及時體現出開關狀態變化的影響。進一步驗證了所提方法的正確性。

5 結 論

本文通過分析，認為在開關狀態改變時刻前后，橋臂電流不突變及電容電壓不突變，修正了電容電流的計算公式，有效地消除了梯形積分計算過程中采用開關狀態改變前時刻的值進行計算而引入的計算誤差，并在PSCAD/EMTDC平臺上搭建了MMC等效橋臂模型和單端101電平MMC-HVDC系統，驗證了本文提出的改進計算模型的正確性。

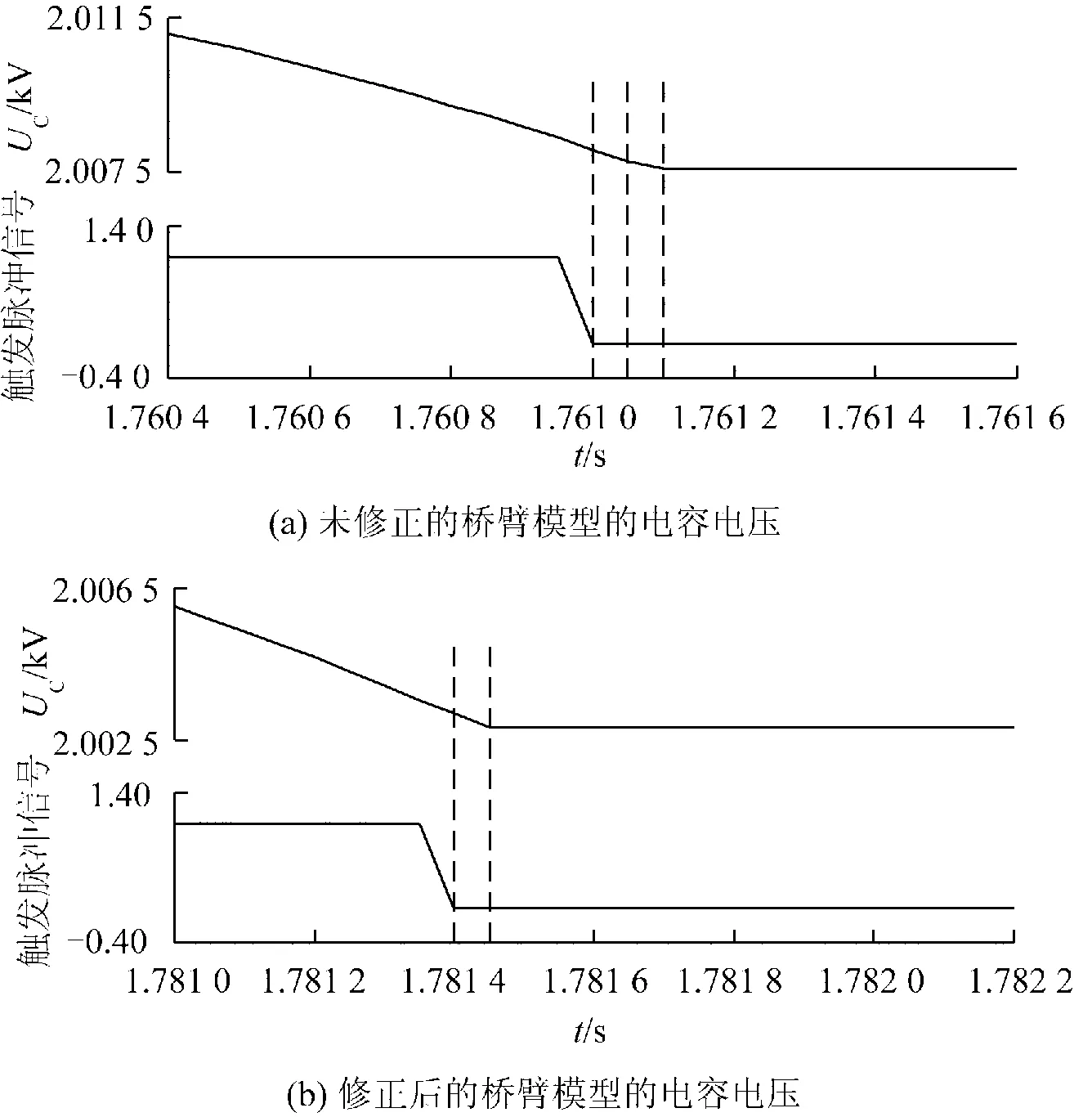
圖9 電容電壓對比Fig.9 Comparison of capacitor voltage

[1]文俊, 殷威揚, 溫家良, 等. 高壓直流輸電系統換流器技術綜述[J]. 南方電網技術, 2015, 9(2):16-24. WEN Jun, YIN Weiyang, WEN Jialiang, et al. Review of converter technology for HVDC transmission [J]. Systems Southern Power System Technology, 2015, 9(2):16-24.

[2]李廣凱, 江政昕, 趙昕, 等. 電壓源換流器高壓直流輸電的特點與前景[J]. 南方電網技術, 2011, 5(5):13-17. LI Guangkai, JIANG Zhengxin, ZHAO Xin, et al. The characteristics and prospect of VSC-HVDC power transmission [J]. Southern Power System Technology, 2011, 5(5):13-17.

[3]李亞樓, 穆清, 安寧,等. 直流電網模型和仿真的發展與挑戰[J]. 電力系統自動化, 2014, 38(4):127-135. LI Yalou, MU Qing, AN Ning, et al. Development and challenge of modeling and simulation of DC grid [J]. Automation of Electric Power Systems, 2014, 38(4):127-135.

[4]李威, 李庚銀. MMC-HVDC電磁暫態仿真模型比較分析研究[J]. 華北電力大學學報(自然科學版), 2015, 42(1):7-14. LI Wei, LI Gengyin. Research on Comparativeanalysis of MMC-HVDC electromagnetic transient simulation models [J]. Journal of North China Electric Power University, 2015, 42(1): 7-14.

[5]GNANARATHNA U N，GOLE A M，JAYASINGHE R P.Efficient modeling of modular multilevel HVDC converters (MMC) on electromagnetic transient simulation programs [J].IEEE Transactions on Power Delivery，2011，26(1)：316-324.

[6]許建中, 趙成勇, 劉文靜. 超大規模MMC電磁暫態仿真提速模型[J]. 中國電機工程學報, 2013, 33(10):114-120. XU Jianzhong, ZHAO Chengyong, LIU Wenjing, et al. Accelerated model of ultra-large scale MMC in electromagnetic transient simulations [J]. Proceedings of the CSEE, 2013, 33(10):114-120.

[7]王鵬伍, 崔翔. 模塊化多電平換流器的時域等效模型及其快速算法[J]. 電網技術, 2013, 37(8):2180-2186. WANG Pengwu, CUI Xiang. Atime-domain equivalent model of modular multilevel converter and its fast algorithm [J]. Power System Technology, 2013, 37(8): 2180-2186.

[8]許建中,趙成勇, GOLE A M. 模塊化多電平換流器戴維南等效整體建模方法[J]. 中國電機工程學報, 2015, 35(8):1919-1929. XU Jianzhong, ZHAO Chengyong,GOLE A M. Research on the Thévenin’s equivalent based integral modelling method of the modular multilevel converter (MMC) [J]. Proceedings of the CSEE, 2015, 35(8): 1919-1929.

[9]趙成勇, 李路遙, 翟曉萌, 等. 一種新型模塊化多電平換流器子模塊拓撲[J]. 南方電網技術, 2012, 6(6):62-66. ZHAO Chengyong, LI Luyao, ZHAI Xiaoming,et al. A new scheme of sub-module topology for modular multi-level converter [J]. Southern Power System Technology, 2012, 6(6): 62-66.

[10]許建中, 李承昱, 熊巖, 等. 模塊化多電平換流器高效建模方法研究綜述[J]. 中國電機工程學報,2015, 35(13):3381-3392. XU Jianzhong, LI Chengyu, XIONG Yan,et al. A review of efficient modeling methods for modular multilevel converters [J]. Proceedings of the CSEE, 2015, 35(13): 3381-3392.

[11]薛英林, 吳方劼, 張濤,等. 基于PSCAD/EMTDC的多端柔性直流輸電系統并行仿真計算[J]. 電力建設, 2016, 37(2):10-17. XUE Yinglin, WU Fangjie, ZHANG Tao, et al. Parallel simulation of multi-terminal MMC-HVDC system based on PSCAD/EMTDC [J]. Electric Power Construction,2016, 37(2):10-17.

[12]徐政, 李寧璨, 肖晃慶,等. 大規模交直流電力系統并行計算數字仿真綜述[J]. 電力建設, 2016, 37(2):1-9. XU Zheng, LI Ningcan, XIAO Huangqing, et al. A review of parallel computing digital simulation of large-scale AC/DC power system [J].Electric Power Construction, 2016, 37(2):1-9.

[13]宋炎侃, 陳穎, 黃少偉,等. 大規模電力系統電磁暫態并行仿真算法和實現[J]. 電力建設, 2015, 36(12):9-15. SONG Yankan, CHEN Ying, HUANG Shaowei, et al. Electromagnetic transient parallel simulation zlgorithm and implementation for large-scale power system [J]. Electric Power Construction, 2015, 36(12):9-15.

[14]姚蜀軍, 韓民曉, 汪燕,等. 大規模電網電磁暫態快速仿真方法[J]. 電力建設, 2015, 36(12):16-21. YAO Shujun, HAN Mingxiao, WANG Yan, et al. A fast electromagnetic transient simulation of large-scale power system [J]. Electric Power Construction, 2015, 36(12):16-21.

[15]趙帥, 賈宏杰, 李鵬, 等. 一種考慮多重開關動作的變步長電磁暫態仿真算法研究[C]//中國電工技術學會學術年會:新能源發電技術論壇論文集. 北京：中國電工技術學會, 2013.

郭琦 (1979)，男，高級工程師(教授級)，博士，研究方向為高壓直流控制保護技術和電網仿真技術研究等；

王嘉鈺(1990)，女，碩士研究生，研究方向為柔性直流輸電系統控制策略；

林雪華(1988)，女，碩士研究生，研究方向為柔性直流仿真建模與控制保護技術研究；

李巖(1973)，男，高級工程師(教授級)，博士，從事高壓直流輸電、柔性直流輸電和電力系統分析方面的研究工作；

劉崇如(1977)，女，教授，博士，從事交直流混合系統分析與仿真、運行與控制的科研與教學工作。

(編輯 張小飛)

Improvement of High-Efficiency Electromagnetic Transient Model Simulation Precision of MMC

GUO Qi1, WANG Jiayu2, LIN Xuehua1, LI Yan1, LIU Chongru2

(1. Electric Power Research Institute, CSG, Guangzhou 510080, China;2. School of Electrical and Electronic Engineering, North China Electric Power University, Beijing 102206,China)

This paper analyzes the mathematical principle of the electromagnetic transient simulation detailed model of modular multilevel converter (MMC) arm based on the Thevenin’s equivalent principle. It is found that when the network structure changes caused by fault or switch of breakers during simulation process, the calculation error may be introduced when using trapezoidal integration method because of the mutation of the capacitor current. To solve the problem, this paper proposes a method to eliminate the calculation error through solving the non-state variable after the mutation. We compare the capacitor voltage before and after the elimination of the calculation error at the moment of switch changing in PSCAD/EMTDC, and verify the correctness and validity of the method. Meanwhile, we establish a single-terminal 101-level MMC-HVDC simulation system, whose results verify the correctness of the proposed improved calculation model.

modular multilevel converter (MMC); Thevenin’s equivalent; trapezoidal integration method; calculation error; simulation precision

南方電網科技項目(大容量高電壓柔性直流輸電關鍵技術及工程應用研究)(CSGTRC-K142031)

TM 743

A

1000-7229(2016)06-0049-06

10.3969/j.issn.1000-7229.2016.06.008

2016-01-25