重載航空負載模擬器非線性最優前饋補償控制

歐陽小平， 李鋒， 朱瑩， 楊上保， 楊華勇

1.浙江大學 流體動力與機電系統國家重點實驗室， 杭州 310027 2.航空機電系統綜合航空科技重點實驗室， 南京 211100

重載航空負載模擬器非線性最優前饋補償控制

歐陽小平1,*， 李鋒1， 朱瑩2， 楊上保2， 楊華勇1

1.浙江大學 流體動力與機電系統國家重點實驗室， 杭州 310027 2.航空機電系統綜合航空科技重點實驗室， 南京 211100

重載航空負載模擬器是用來模擬“C919”、“運-20”等重載飛機舵面工作載荷的地面仿真平臺。設計了一種重載航空負載模擬器，采用非對稱缸作為執行機構以在小體積下完成大載荷加載。為了消除多余力對重載航空負載模擬器加載精度的影響，分析了非對稱缸正反向運動和大載荷變化下伺服閥流量增益的非線性變化對前饋補償函數的影響，并設計了非線性參數估計控制器。同時分析了加速度等動態參數變化和靜態參數的誤差對多余力消除的影響，設計了參數最優控制器。仿真和試驗結果均表明，相比于傳統前饋補償控制器，所設計的非線性最優前饋補償控制器下的加載精度和多余力抑制能力提高了50%以上。

重載； 負載模擬器； 多余力； 非線性控制； 前饋控制

研制和發展大飛機，不僅是快速增長的航空市場的需求，也是促進產業發展和多學科進步的需求。民用大飛機“C919”、軍用大飛機“運-20”等重載飛機的發展在應對搶險救災、人道援助等方面具有重要意義[1]。重載航空負載模擬器主要是用來在重載飛機地面測試時，為舵面加載飛行狀況下的負載，測試飛機舵面在帶載狀態下的可靠性和控制性能。重載航空負載模擬器的研制能夠縮短重載飛機的研制周期，對于重載飛機的發展意義重大[2-4]。

重載航空負載模擬器是一種典型的位置干擾力(矩)控制系統。在整個加載過程中，由于需要跟隨位置系統移動，因此產生了強迫流量從而產生多余力,對于整個加載精度造成很大影響。當進行大功率、重載試驗時，多余力甚至高達加載值的5～10倍，因此消減多余力是負載模擬器研制的關鍵[4-5]。針對多余力消除的問題，國內外進行了深入的研究，其方法主要分為3類：

1) 文獻[6]利用位置同步馬達來實現位置跟蹤，然后在其轉子上再安裝一個加載馬達完成系統加載。文獻[7]采用雙閥控制原理，兩個閥分別完成位置跟蹤和系統加載。這類方法通過附加硬件來完成位置跟蹤，結構復雜，成本較高。

2) 文獻[8-9]采用了定量反饋理論(QFT)設計了控制器，文獻[10-12]采用非線性魯棒控制、文獻[13-15]采用了模糊控制方法以及文獻[16-17]采用了神經網絡控制方法來消除多余力。這類方法將多余力看作干擾力，利用智能算法來完成控制，對控制器要求較高。

3) 文獻[18]對閥控非對稱缸被動式加載系統建立了數學模型，采用雙向前饋補償控制器進行控制。文獻[19]在傳統的速度同步控制基礎上，增加了舵面與加載系統的速度差進行二次補償。文獻[20]采用自適應非線性優化補償控制，該方法將加載力誤差最小化作為系統的控制目標，在動態加載的過程中對非線性參數實時估計。這類方法均是在速度補償控制的基礎上，利用自適應等方法進行改進，方法簡單、效果明顯且對控制器要求較低。

以雙出桿缸或液壓馬達作為負載模擬器執行機構的輕載負載模擬器已經取得了大量的研究成果，但對于“C919”和“運-20”等重載飛機舵面需要承受重載的場合，目前能夠實現大載荷加載的負載模擬器的相關研究還很少。如何在有限的空間內完成大載荷加載，以及大載荷變化時能否完成高精度的跟蹤性能是重載航空負載模擬器研制過程中遇到的兩個難點。

針對以上問題，本文采用非對稱缸作為負載模擬器執行機構，在小空間內完成重載荷加載。采用非線性最優前饋補償控制器，有效抑制多余力并實現在大載荷變化時良好的跟蹤性能。

1 系統數學模型及補償環節分析

1.1 數學模型

航空負載模擬器結構如圖1所示，左側為力加載系統，右側為舵面系統。兩套系統剛性連接，均采用伺服閥來控制非對稱缸運動。兩套系統中間安裝一個力傳感器來完成力閉環控制，舵面系統的非對稱缸內安裝一個位移傳感器來完成位移閉環控制。

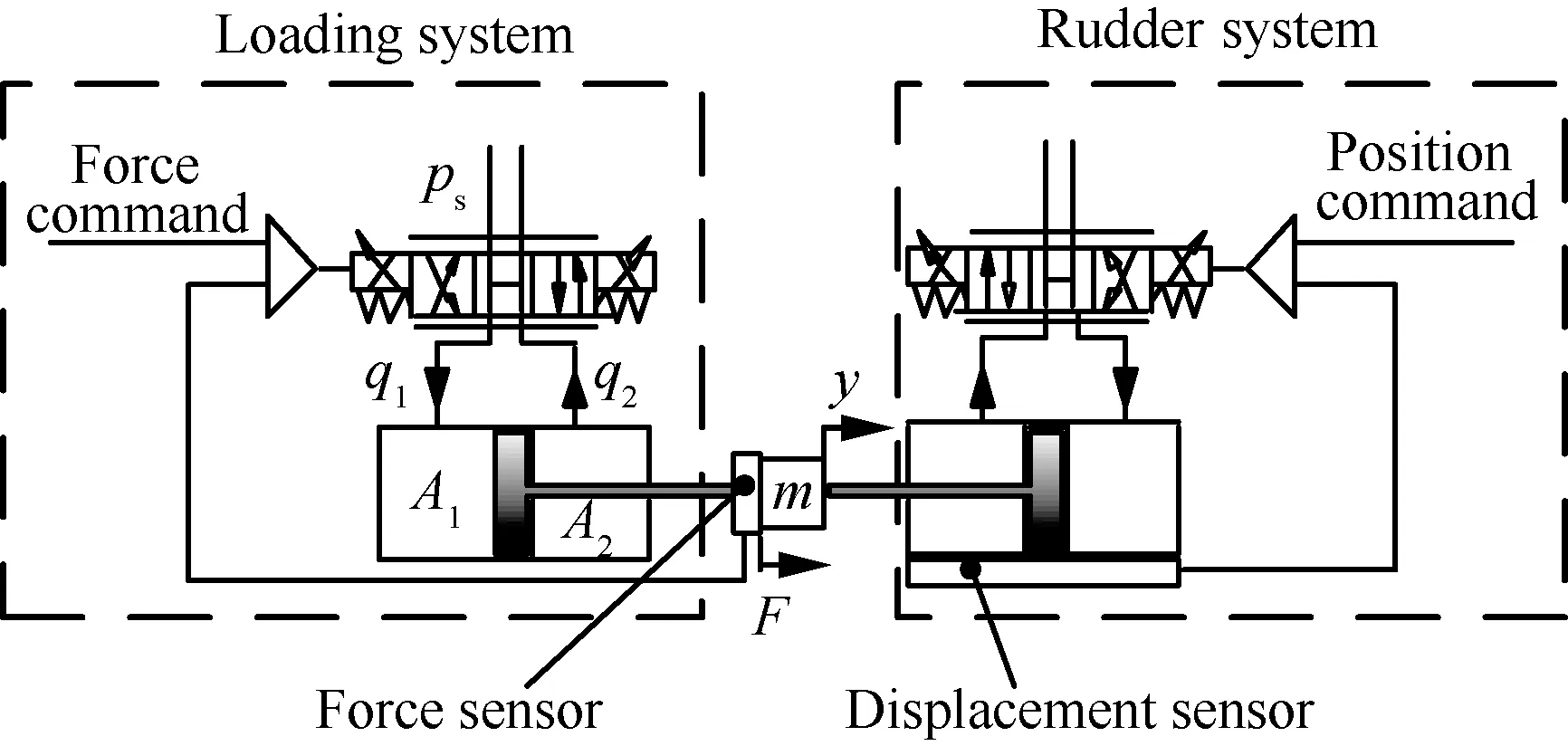
圖1 航空負載模擬器結構

Fig.1 Architecture of aviation load simulator

由伺服閥節流口方程可得

(1)

式中：q1和q2分別為流入加載缸無桿腔和流出有桿腔流量，m3/s；p1和p2分別為加載缸無/有桿腔壓力，Pa；ps為供油壓力，Pa；Cd為加載閥流量系數；xv為加載閥閥芯位移，m；ω為加載閥窗口梯度；ρ為油液密度，kg/m3。

因為運動產生的容積變化較小可忽略，根據液壓缸流量連續性方程可得

(2)

式中：A1和A2為加載缸無/有桿腔面積，m2；Vt為加載缸兩腔的容積，m3；βe為系統油液彈性模量，Pa；Cip為加載缸內泄系數，m5/(N·s)；y為活塞位移，m；

忽略摩擦力，根據力平衡方程可得

(3)

式中：B為活塞桿與液壓缸之間的黏性阻尼系數， N·s/m；m為兩系統活塞桿、液壓質量以及慣性負載折算質量，kg；F為舵面系統所受加載力，N。

根據式(1)～式(3)，得到負載模擬器模型框圖如圖2所示，圖中：U為伺服閥輸入電壓。

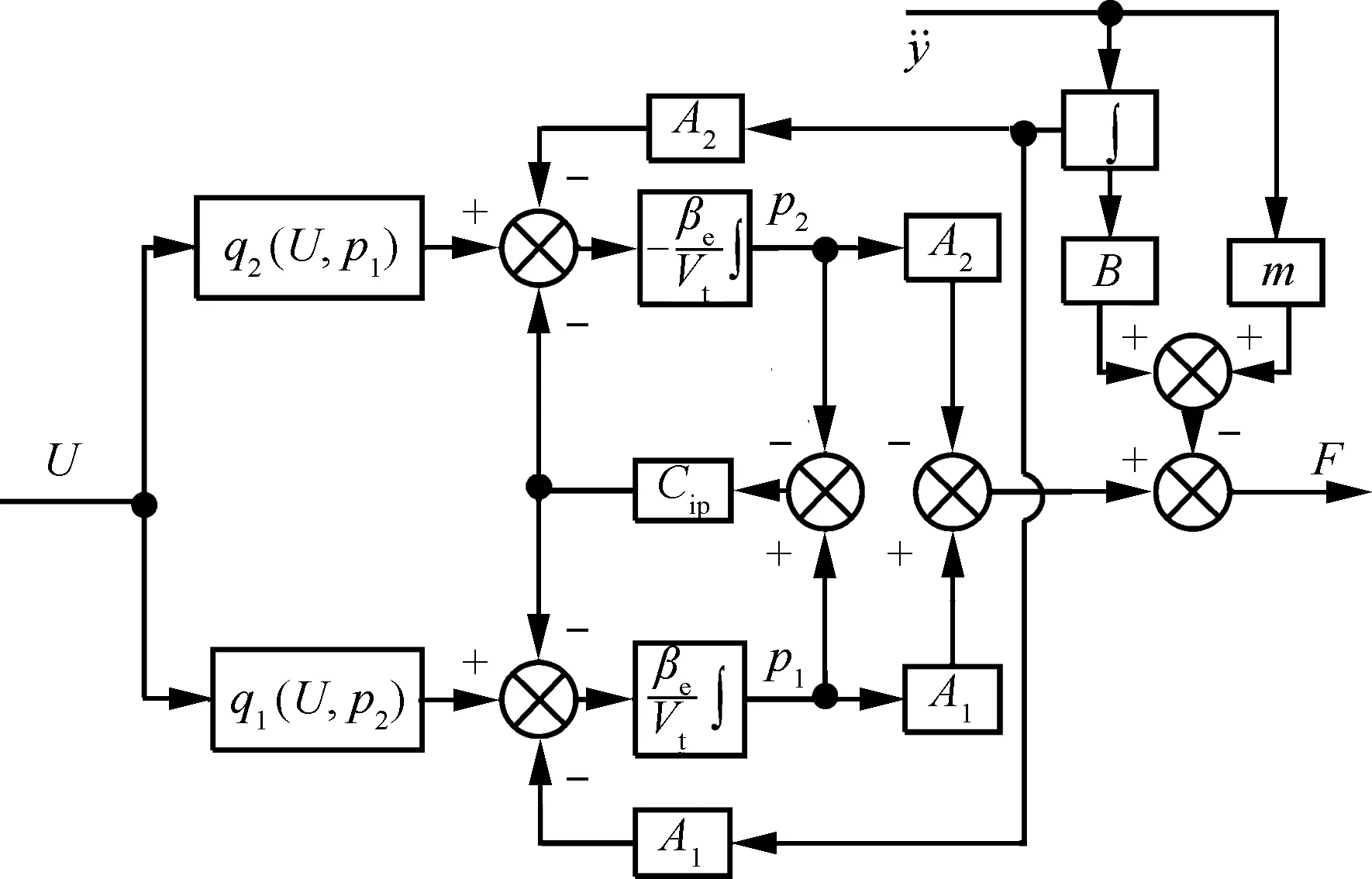
圖2 負載模擬器模型框圖

Fig.2 Block diagram of load simulator model

從圖2中可以看出，當舵面系統工作而力加載系統不工作時，由于兩套系統之間存在一種強耦合關系，力加載系統也會產生一定的多余力。舵面系統的運動會對力加載系統的加載精度產生巨大的影響。為了定量地描述兩套系統相互之間的耦合關系以及其動態特性，根據能量守恒定律定義負載壓力和流量[21]分別為

(4)

(5)

式中：n為加載缸有桿腔與無桿腔的面積比；pL為加載缸負載壓力，Pa；qL為加載缸負載流量，m3/s。

當系統運動擾動較小時，伺服閥閥口工作在零位附近，綜合式(1)、式(4)和式(5)并正反向分別線性化可得伺服閥流量線性化方程[22]為

(6)

式中：Kq為加載伺服閥流量增益，m2/s；Kc為加載伺服閥流量-壓力系數，m5/(N·s)。

綜合式(1)、式(2)和式(5)，可得液壓缸流量連續性方程為

(7)

式中：Ct和Cts均為內泄負載壓力等效系數， m5/(N·s)。

為了避免運動擾動激發伺服閥的動態特性，采用了高頻響伺服閥，其頻寬遠大于系統工作頻率，故可以認為是一個線性環節。

xv=KvU

(8)

式中：Kv為伺服閥閥芯增益系數，m/V。

將式(3)、式(6)～式(8)合并，并進行Laplace變換后整合可得

(9)

式中：

1.2 前饋補償環節分析

從式(9)中可以看出，加載力由兩部分組成：伺服閥閥芯動作控制的力和由舵面系統運動產生的干擾力，即多余力Fad：

(10)

從式(10)的分子中可以看出，多余力與舵面系統運動速度、加速度以及加速度變換率有關。

為了消除多余力，通常利用前饋補償控制器，其基本原理如圖3，是用速度信號作為前饋補償控制器的輸入，經過前饋控制器運算后，輸出值作為補償值來完成系統的速度同步控制。

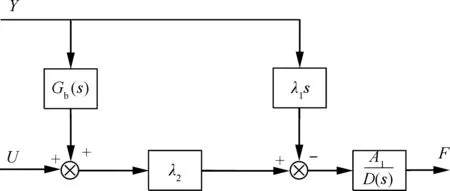
圖3 前饋補償原理圖

Fig.3 Diagram of feedforward compensation principle

根據結構不變性原理和圖3可得前饋補償函數為

(11)

2 非線性補償控制器

由式(11)可知，前饋補償控制器設計存在兩個問題：

1) 前饋補償函數分子項λ1s與速度、加速度以及加加速度有關。若要完全補償，需要對位置信號做二次微分以及三次微分，但由于噪聲的存在，將很難保證精度。此外，加工和參數測量的誤差以及活塞缸運動時容積的時變特性也會對前饋補償函數產生影響。

2) 由前饋補償函數分母項λ2可知，非對稱缸在載荷大范圍變化時，流量增益Kq會隨著負載和運動方向變化實時發生非線性變化，從而導致前饋補償函數發生非線性變化。針對非對稱缸負載模擬器執行機構的情況，傳統上常采用雙向不同固定值切換前饋補償，對于載荷小范圍變化時可以獲得較好的效果，但對于非對稱缸在大載荷變化工況下就難以取得良好效果，在一些極端工況下甚至失效。

為了方便描述以上兩種因素對多余力消除產生的影響，定義λ1為多余力干擾系數、λ2為非線性干擾系數。

非線性最優前饋補償控制器如圖4所示，在PID控制器的基礎上，利用參數最優化控制器克服λ1變化產生的影響，利用非線性參數估計控制器克服λ2變化產生的影響。通過力傳感器獲得所需的力信號并與力控制信號Fc對比計算所需的力偏差值e；通過位移傳感器來獲得位移信號并與位置控制指令yc對比完成位置控制。

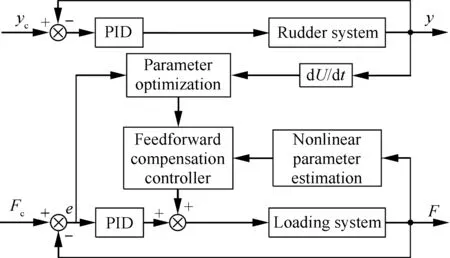
圖4 非線性最優前饋補償控制器

Fig.4 Nonlinear optimal feedforward compensation controller

2.1 參數最優化控制器

當實現完全前饋補償時，Gb(s)=λ1s/λ2。由于多余力干擾系數λ1既與A1、m、B和ps等靜態參數有關，也與加速度和加速度變化值等動態參數有關，由式(9)得到的參數在實際應用時很難獲得完全補償。

根據式(10)分析可得

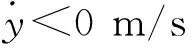
欠補償時(Gb(s)<λ1s/λ2)，通過PID控制器力靜態值跟蹤偏差e>0 N；過補償時(Gb(s)>λ1s/λ2)，則通過PID控制器力靜態值跟蹤偏差e<0 N。

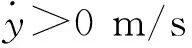
欠補償時(Gb(s)<λ1s/λ2)，通過PID控制器力靜態值跟蹤偏差e<0 N；過補償時(Gb(s)<λ1s/λ2)，則通過PID控制器力靜態值跟蹤偏差e>0 N。

對于一般負載模擬器，系統在20 Hz運動擾動時，多余力主要由于速度項產生，加速度以及加加速度產生的多余力只占總多余力的1%左右。因此，當加速度以及加加速度在高頻小幅度變化時，對系統產生的影響較小。只要在初始調節完成后，飛行舵面處于正常運行時，參數動態變化、加速度以及加加速度并不會導致多余力干擾系數發生十分迅速的變化。

綜合上述分析，為了實現完全補償，根據運動方向以及偏差信息，采用步進式參數尋優方法，實時調整干擾系數λ1，可以有效抑制多余力。設計參數最優化控制器為

(12)

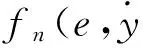
綜合式(9)和式(12)可得

(13)

2.2 非線性參數估計控制器

根據式(9)可知，非線性干擾系數λ2與Kq、Kv有關，其中Kv為靜態變量，故當載荷變化時只有Kq將發生變化。

通過式(6)中的定義可知，對于絕大多數確定的pL，當閥芯向不同方向運動時，Kq會發生躍變；在同一方向運動且載荷變化大時，pL發生較大變化，Kq會發生非線性變化。

由伺服閥節流口方程和式(8)可得

(14)

式中：qn為伺服閥額定流量，m3/s；Δpn為伺服閥額定流量下的壓降，Pa；Umax為伺服閥最大輸入電壓，V。

綜合式(4)、式(8)、式(9)和式(14)可得

(15)

式中：

2.3 穩定性分析

由于前饋補償控制器和非線性參數估計控制器均為開環控制，本身并不會對系統穩定性產生影響。只有參數最優控制器，利用偏差信號形成步進式閉環控制，會對系統的穩定性產生影響。

忽略參數最優化開啟閾值，結合式(9)和式(11)，可知參數最優控制器輸入輸出傳遞函數為

(16)

由于本文設計的參數最優控制器是基于步進尋優，故相當于被積函數為符號函數的積分器。代入系統參數，速度取研究對象最大值，得到前饋補償函數的Bode圖，如圖5所示。從圖5中可以看出，系統最大相角為-180°，系統全頻穩定。當系統自身運動變化導致的輸入量變化時，系統屬于低頻段，具有幅值增量大、穩定性余量大的特點。

此外，為了抑制由于采用步進式積分器而導致的輸入量自身振蕩，本文設置了尋優開啟閾值。若開啟閾值大于最小步長產生的偏差，當系統偏差在開啟閾值以內時，參數最優控制器輸出值為固定值不會產生振蕩，這時非線性最優補償控制器僅為一個開環控制器，不會影響系統的穩定性。

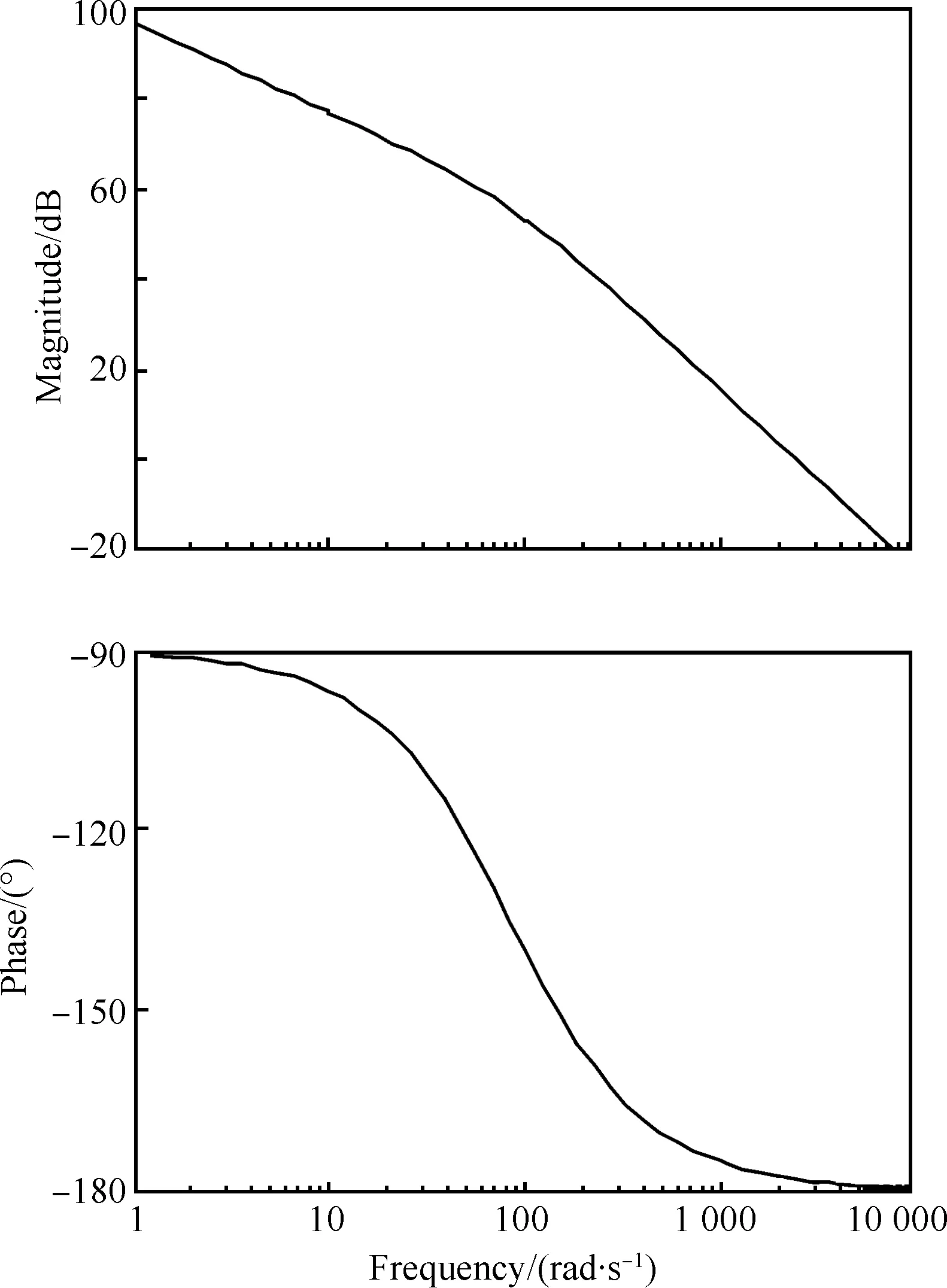
圖5 前饋補償函數的Bode圖

Fig.5 Bode diagram of feedforward compensation function

3 仿真分析

3.1 參數設置

基于MATLAB Simulink軟件平臺，根據圖2 所示的非線性數學模型搭建系統仿真模型，模型參數如表1所示。PID控制器比例參數KP和積分參數KI通過齊格勒-尼柯爾斯法則整定，固定補償控制器以空載狀態正向運動進行設計，雙向補償控制器以空載狀態設計其正反向非線性干擾系數λ2±。在正常工況下，速度項以外項產生的多余力只占總多余力1%，PLC循環周期為0.8 ms，為了調整的快速性和系統跟蹤的準確性，設f0(e,y)=A1，f為A1的1‰。根據多余力控制15%精度，eh取加載幅值的1%，當處于研究對象的最大速度，步長f對應的力步進變化穩態值為36.33 N，為防止產生振蕩，eh取最小值為100 N，控制器具體參數如表2。

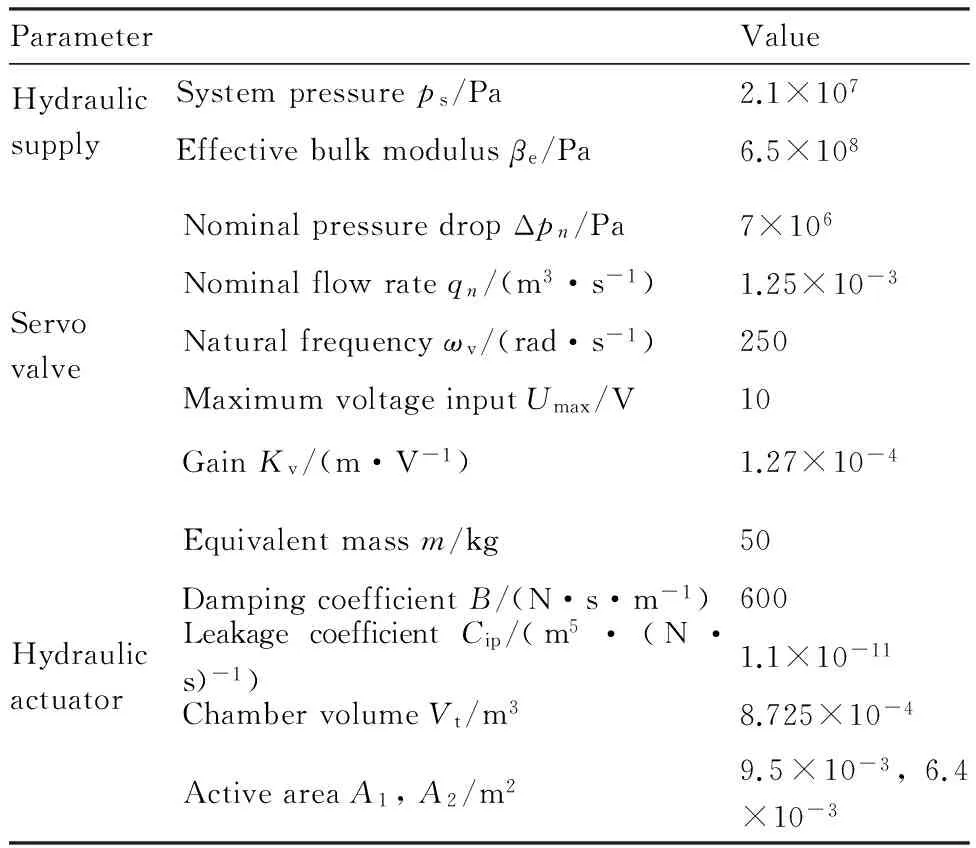
表1 仿真模型參數

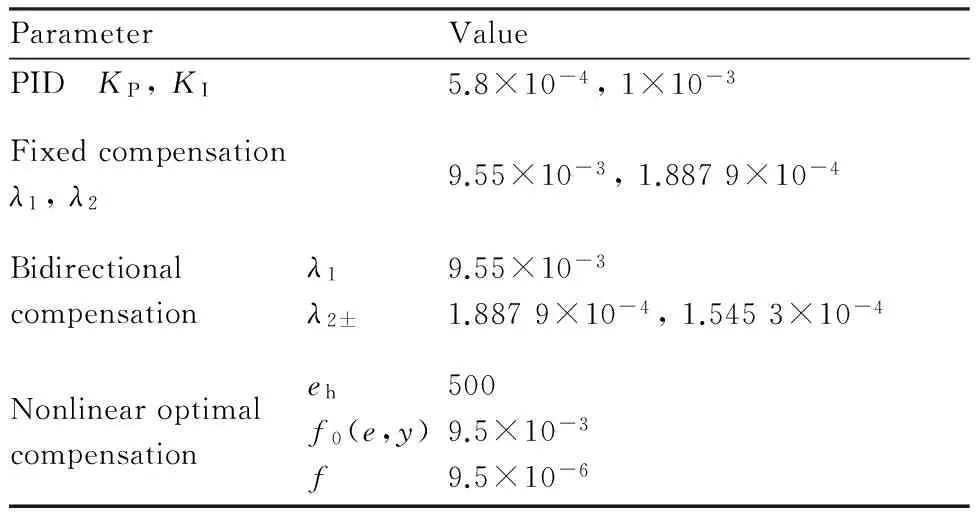
表2 控制器參數

3.2 仿真分析

為了測試控制效果的有效性，共進行6組試驗，試驗結果如圖6～圖9所示。

3.2.1 多余力干擾系數影響仿真分析

在1 Hz、5 mm正弦位置干擾情況下，力恒值0 N 加載，多余力曲線如圖6所示。由非線性參數估計控制器確定非線性干擾系數λ2，多余力干擾系數λ1分別取0.01，0.009 6，0.009。3種狀態下，最大多余力分別為同向850 N，反向400 N，反向1 480 N。從3組曲線的對比中可以看出，當多余力干擾系數偏小時，前饋補償不足，從而導致系統仍有較大的反向多余力；當干擾系數偏大時，產生前饋過補償，從而導致產生了同向多余力。合適的前饋補償系數能夠大幅減小多余力。

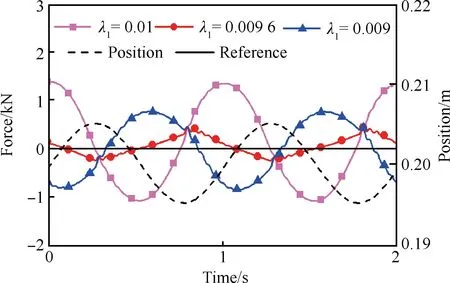
圖6 不同多余力干擾系數影響

Fig.6 Influence of different surplus force coefficients

3.2.2 靜態值跟蹤多余力仿真分析

在1 Hz、5 mm正弦位置干擾情況下，加載系統分別加載恒值50 000，0，-50 000 N，多余力曲線如圖7所示。在0 N的固定值加載下，固定值補償控制器在正向運動時的最大多余力為540 N，但反向時的最大多余力達到了5 800 N；雙向補償控制器正反向運動時的最大多余力均為540 N。通過兩者對比可以得出，非對稱缸正反向運動時動態參數的變化使得一個前饋補償系數在正向運動時得到合適的補償，但反向時將會產生較大的多余力。對比圖7中的3幅圖可以發現，雙向補償控制器在50 000，0，-50 000 N 加載時的最大多余力分別為4 200，540，6 500 N；非線性控制器在3種加載狀態下的最大多余力均為450 N。說明在加載力大范圍變化時，系統流量增益發生了較大變化，從而導致一個固定補償系數在0 N狀態下能夠得到合適的補償；但在±50 000 N 時，補償效果減弱，存在較大多余力，而非線性控制器在加載力變化較大時均能夠跟蹤系統的變化，大幅消除多余力。

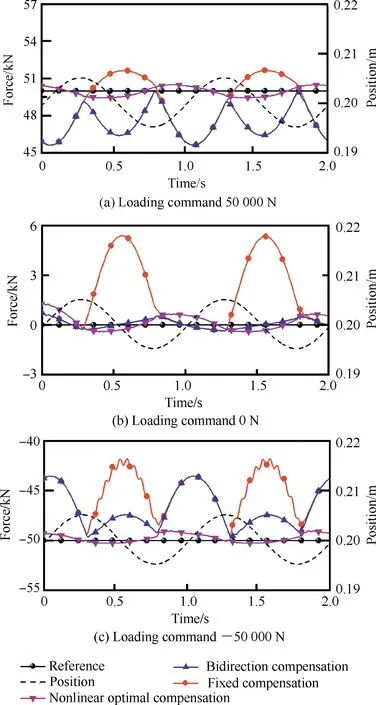
圖7 不同靜態力多余力仿真曲線

Fig.7 Simulation curves of surplus force under different static forces

3.2.3 動態加載跟蹤仿真分析

在0.5 Hz、10 mm正弦位置干擾情況和1 Hz、5 mm正弦位置干擾情況下，0.5 Hz、50 000 N 力的正弦加載跟蹤曲線分別如圖8(a)和圖8(b)所示。從圖8(a)中可以看出，在低頻響大位移干擾加載工況下，雙向補償控制器的最大多余力達到了2 660 N，非線性最優補償控制器正反向的最大多余力僅為1 100 N。從圖8(b)中可以看出，在高頻響小位移干擾加載工況下，雙向補償控制器的最大多余力達到了6 000 N，而非線性最優補償控制器最大多余力僅為2 100 N。在兩種工作條件下，非線性最優補償控制器相比于雙向補償控制效果，其多余力消除分別提高了58.7%和68.7%。

圖8 不同情況下正弦加載(0.5 Hz、 50 000 N)的仿真結果

Fig.8 Simulation results under sine loading (0.5 Hz， 50 000 N) of different cases

在變幅值0.5 Hz正弦位置干擾情況下，5 000 N/mm 梯度力加載跟蹤曲線如圖9所示。

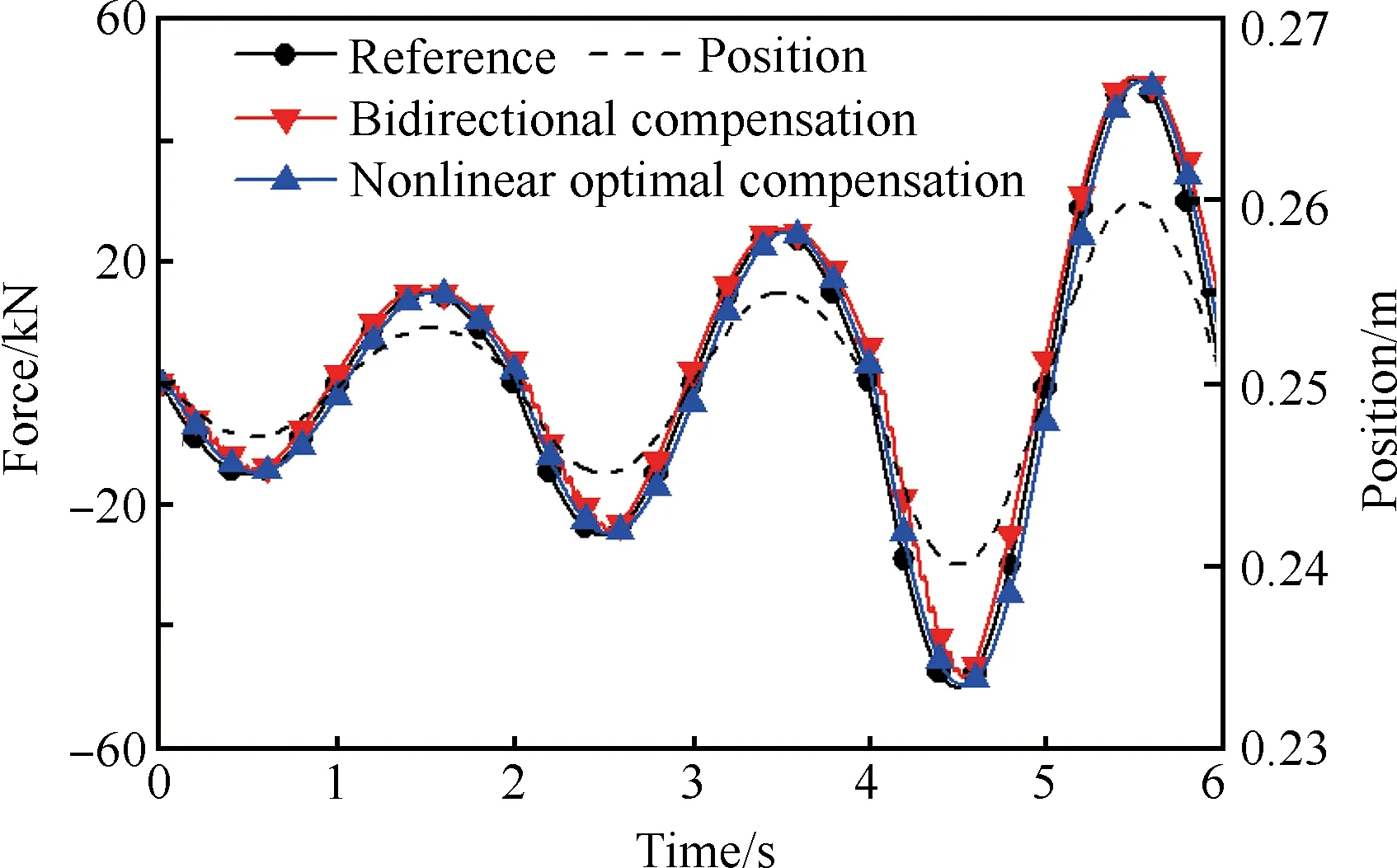
圖9 變幅值正弦干擾下5 000 N/mm加載梯度仿真曲線

Fig.9 Simulation curves under variable amplitude position disturbance and 5 000 N/mm loading gradient

從圖9中可以看出，在變幅值正弦加載過程中，雙向補償控制器的最大多余力達到了6 600 N，而非線性最優補償控制器正反向的最大多余力僅為3 200 N。相比于雙向補償控制器，非線性最優補償控制器的多余力消除效果在幅值增大時較為明顯，幅值最大時多余力抑制效果提高了51.5%。

4 試驗分析

4.1 試驗臺

圖10 試驗臺

Fig.10 Test rig

負載模擬器試驗平臺如圖10所示，包括底座、左側的負載模擬器和右側舵面系統模擬器。兩套系統之間安裝力傳感器(±300 kN)，舵面系統模擬器作動器內安裝有位移傳感器(0～0.5 m)。伺服閥采用MOOG-G631-3006。采用兩臺恒壓變量泵分別作為舵面系統模擬器和負載模擬器的油源。兩套系統均設置了安全閥(31 MPa)來保證系統安全。兩套系統位移和力由貝加萊CP1484 PLC編程控制。試驗臺還安裝了溫度傳感器、壓力傳感器和轉速傳感器來完成系統工況監測以及一臺工控機來記錄測量數據以及人機交互控制。兩套系統作動器完全一致，系統元件參數如表1所示，系統信號采樣頻率為1 kHz。

4.2 試驗分析

為了驗證控制效果的有效性，共進行5組試驗，所得試驗結果如圖11～圖15所示。

4.2.1 靜態力跟蹤多余力試驗分析

在1 Hz、5 mm正弦位置干擾情況下，加載系統分別加載恒值50 000，0，-50 000 N的多余力測試曲線如圖11所示。

圖11 正弦位移干擾(1 Hz、 5 mm)下的多余力測試曲線

Fig.11 Test curves of surplus force under sine position disturbance (1 Hz, 5 mm)

從圖11中可以看出，系統在0 N定值加載下，雙向前饋補償控制器和非線性最優前饋補償控制器下的最大多余力分別為820 N和800 N；在50 000 N定值加載下，雙向前饋補償控制器和非線性最優前饋補償控制器下的最大多余力分別為3 500 N和1 150 N；系統在-50 000 N定值加載下，雙向前饋補償控制器和非線性最優前饋補償控制器下的最大多余力分別為5 800 N和1 050 N。試驗結果表明，當系統力發生較大變化時，非線性最優補償控制器均能夠使多余力大幅消減，但雙向前饋補償控制器則只能在設計值附近完成有效補償。

4.2.2 動態加載跟蹤試驗分析

在0.5 Hz、10 mm正弦位置干擾情況和1 Hz、5 mm正弦位置干擾情況下，0.5 Hz、50 000 N 力的正弦加載跟蹤曲線分別如圖12(a)和圖12(b)所示。

圖12 不同情況下正弦加載(0.5 Hz、 50 000 N)的試驗結果

Fig.12 Test results under sine loading (0.5 Hz， 50 000 N) of different cases

從圖12(a)中可以看出，在低頻響大位移干擾加載工況下，雙向補償控制器的最大多余力達到了9 200 N，非線性最優補償控制器正反向的最大多余力僅為3 650 N。從圖12(b)中可以看出，在高頻響小位移干擾加載工況下，雙向補償控制器的最大多余力達到了13 000 N，而非線性最優補償控制器的最大多余力僅為5 450 N；在兩種工作條件下，非線性最優補償控制器相比于雙向補償控制效果多余力消除效果分別提高了60.3% 和58.1%。

在變幅值0.5 Hz正弦位置干擾情況下，5 000 N/mm 梯度力加載跟蹤曲線如圖13所示。

從圖13中可以看出，在變加載過程中，雙向補償控制器的最大多余力達到了11 000 N，非線性最優補償控制器正反向的最大多余力僅為 5 200 N。非線性最優補償控制器相比于雙向補償控制效果多余力消除效果在幅值增大時較為明顯，幅值最大時多余力抑制效果提高了52.7%。

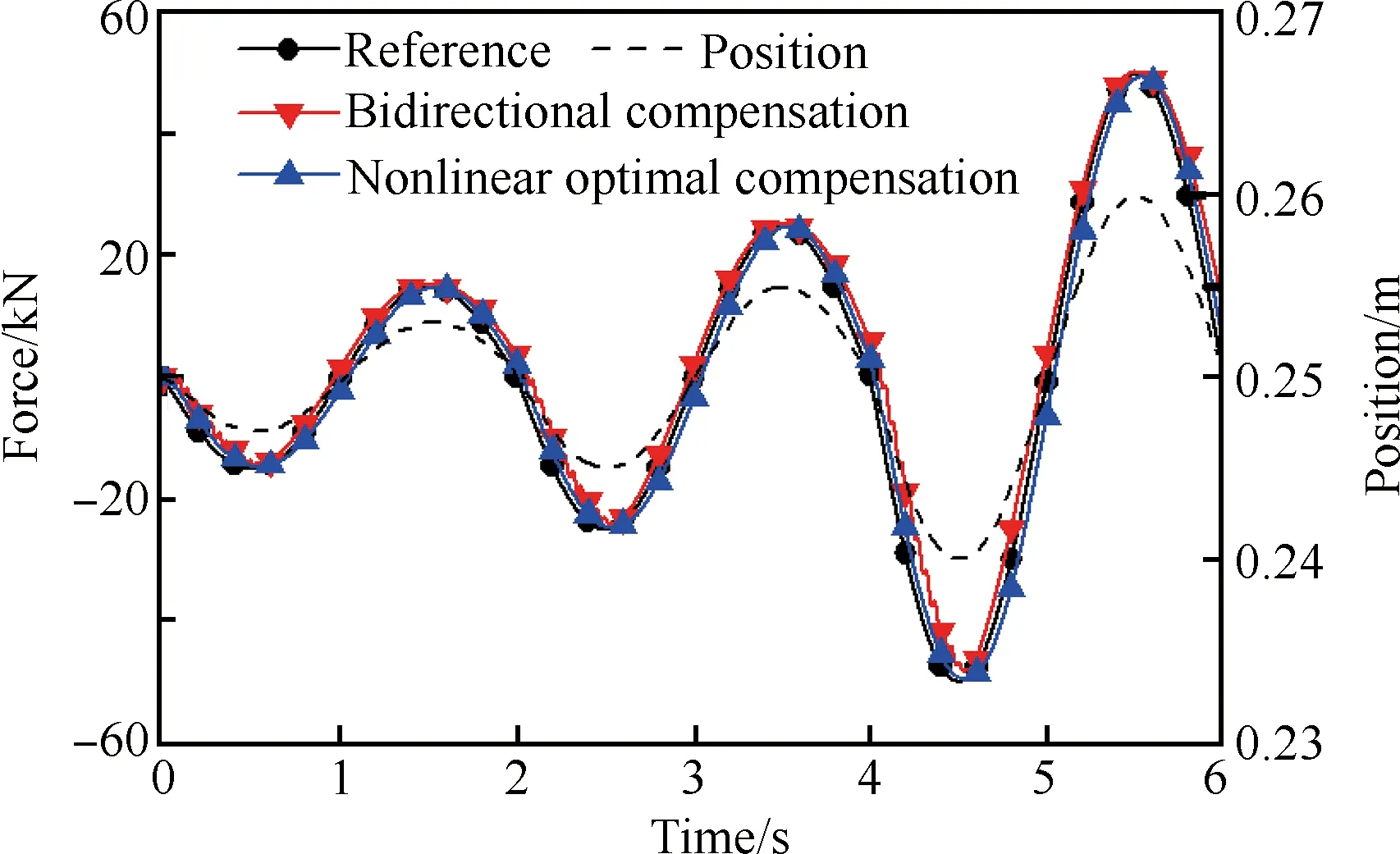
圖13 變幅值正弦干擾下5 000 N/mm加載梯度試驗曲線

Fig.13 Test curves under variable amplitude position disturbance and 5 000 N/mm loading gradient

4.2.3 試驗與仿真對比分析

在不同正弦位置干擾情況下，0.5 Hz、50 000 N 正弦加載仿真和試驗對比曲線如圖14所示。變幅值正弦位置干擾、定加載梯度仿真和試驗對比曲線如圖15所示。

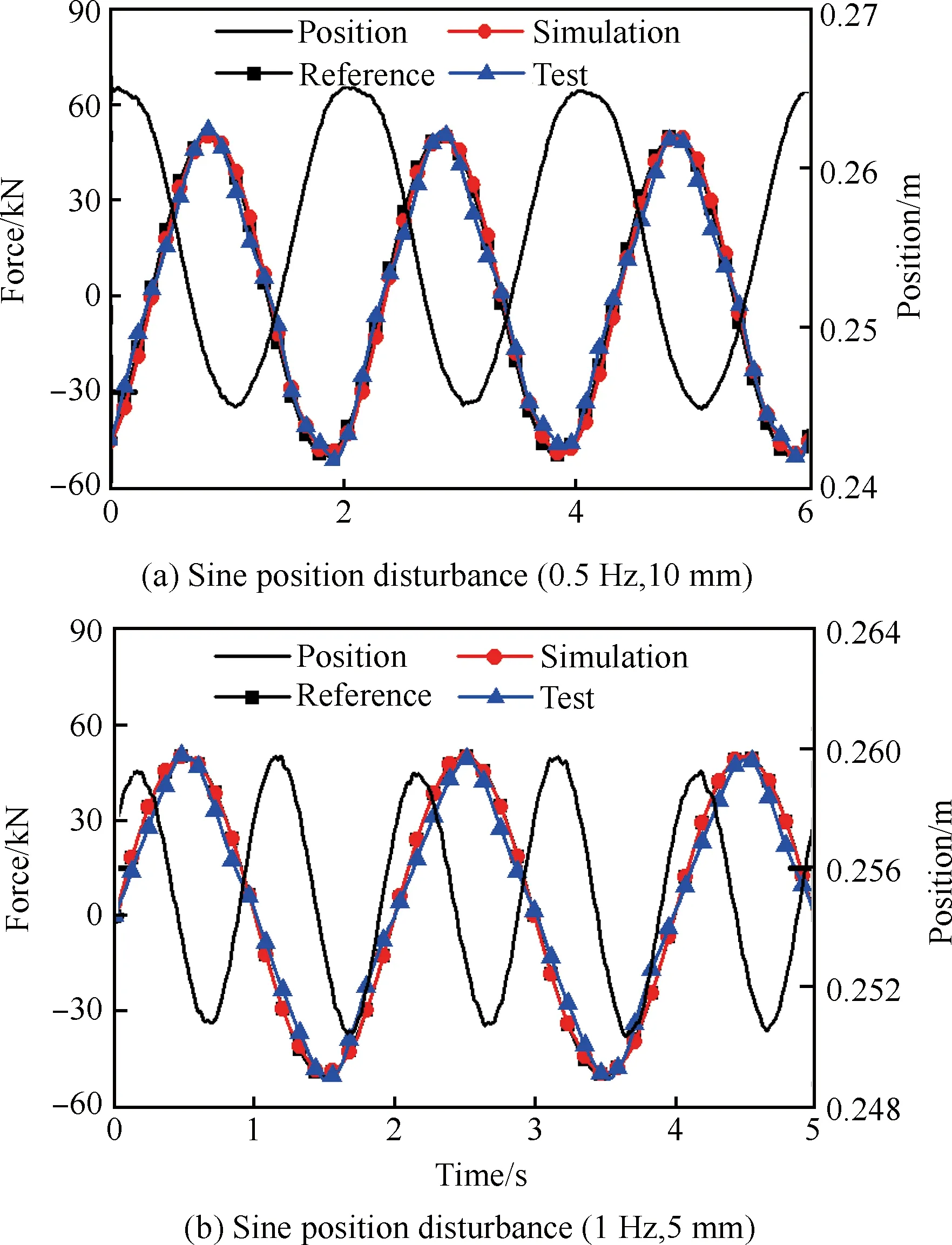
圖14 正弦加載(0.5 Hz、 50 000 N)仿真試驗對比

Fig.14 Comparison between simulation and test results under sine loading (0.5 Hz， 50 000 N)

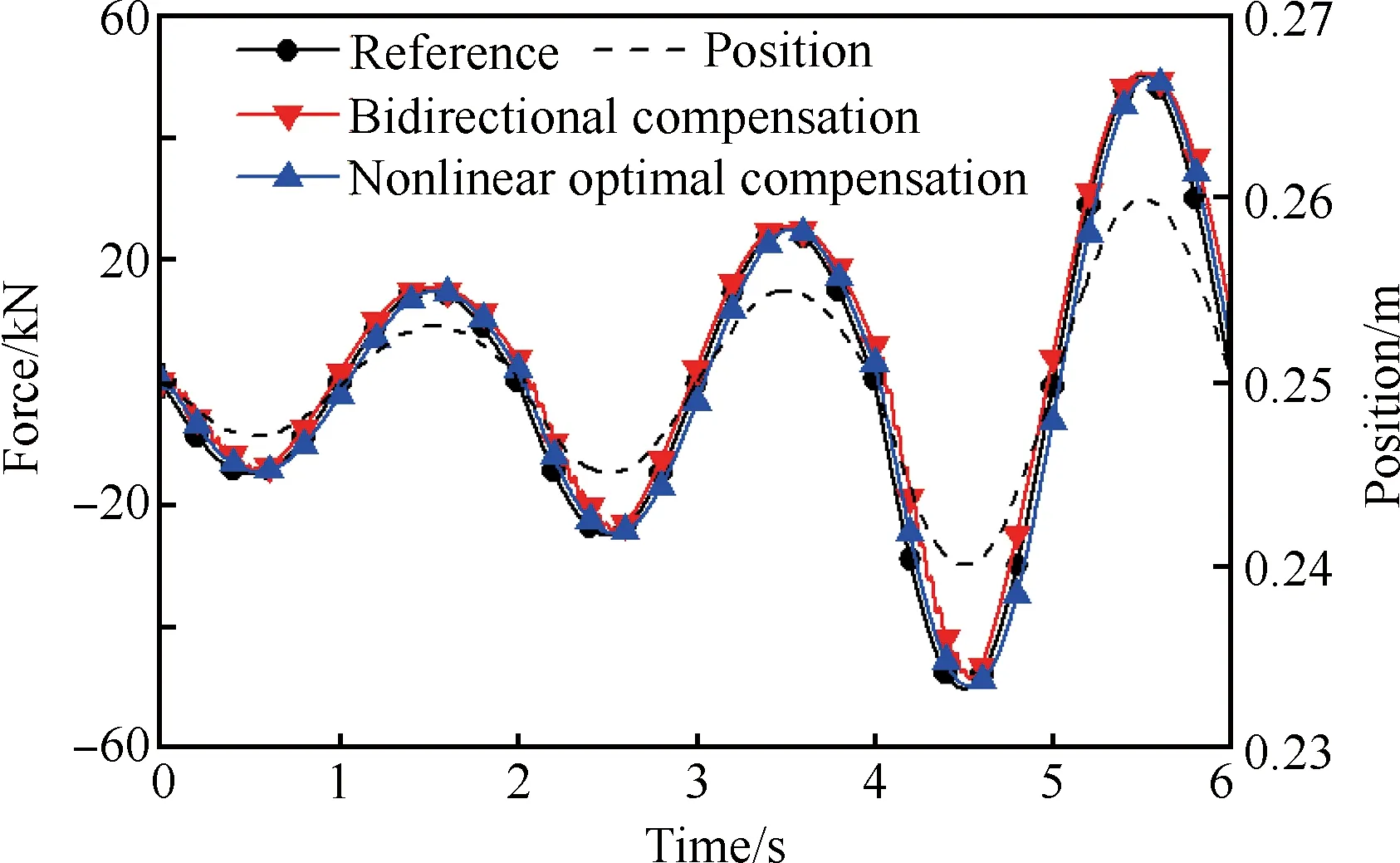
圖15 變幅值正弦干擾下5 000 N/mm加載梯度仿真試驗對比

Fig.15 Comparison between simulation and test results under variable amplitude position disturbance and 5 000 N/mm loading gradient

從圖14和圖15中可以看出，試驗結果相較于仿真結果，跟蹤誤差略微提高，主要是因為試驗中存在噪聲干擾和供油壓力變動等因素。仿真和試驗結果都證明了非線性最優補償控制對于重載航空負載模擬器的有效性。

5 結 論

1) 針對重載航空負載模擬器進行了研究，建立了系統的非線性數學模型，分析了多余力產生的原因，指出了雙向前饋補償控制器應用于重載航空負載模擬器失效的原因是流量增益在非對稱缸正反向運動和大載荷變化情況下發生非線性變化。

2) 分析了參數不確定性和運動過程多余力干擾系數動態變化存在的原因，并指出了這兩者會導致多余力大幅存在。

3) 非線性最優前饋補償控制器在小擾動工況下，能夠實時追蹤系統的變化，做出最優的補償。在非對稱缸作為執行機構，大載荷動態變化的工況下，力跟蹤效果較傳統前饋補償控制器提高50%以上。

[1] 楊華勇, 丁斐, 歐陽小平, 等. 大型客機液壓能源系統[J]. 中國機械工程, 2009, 20(18): 2152-2159. YANG H Y, DING F, OUYANG X P, et al. Hydraulic power systems for trunk line aircrafts[J]. China Mechanical Engineering, 2009, 20(18): 2152-2159 (in Chinese).

[2] WANG C W, JIAO Z X, SHANG Y X, et al. Suppress surplus torque based on velocity closed-loop synchronization[C]//Proceedings of 2011 International Conference on Fluid Power and Mechatronics (FPM). Piscataway, NJ: IEEE Press, 2011: 435-439.

[3] WANG C W, JIAO Z X, WU S, et al. “Dual-loop control” of load simulator[C]//Proceedings of 2012 10th IEEE International Conference on Industrial Informatics (INDIN). Piscataway, NJ: IEEE Press, 2012: 530-535.

[4] AHN K K, TRUONG D Q, THANH T Q, et al. Online self-tuning fuzzy proportional-integral-derivative control for hydraulic load simulator[J]. Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering, 2008, 222(2): 81-95.

[5] 華清. 電液負載模擬器關鍵技術的研究[D]. 北京: 北京航空航天大學, 2001. HUA Q. Studies on the key technology of electrohydraulic load simulator[D]. Beijing: Beijing University of Aeronautics and Astronautics, 2001 (in Chinese).

[6] YU C Y, LIU Q H, ZHAO K D. Velocity feedback in load simulator with a motor synchronizing in position[J]. Journal of Harbin Institute of Technology: New Series, 1998, 3(5): 78-81.

[7] 郝經佳. 雙閥控制在電液負載仿真臺中的應用[J]. 中國機械工程, 2002, 13(10): 814-816. HAO J J. Application of dual valve in electro hydraulic simulator[J]. China Mechanical Engineering, 2002, 13(10): 814-816 (in Chinese).

[8] NAM Y, HONG S K. Force control system design for aerodynamic load simulator[J]. Control Engineering Practice, 2002, 10(5): 549-558.

[9] NIKSEFAT N, SEPEHRI N. Design and experimental evaluation of a robust force controller for an electro-hydraulic actuator via quantitative feedback theory[J]. Control Engineering Practice, 2000, 8(12): 1335-1345.

[10] LI G Q, CAO J, ZHANG B, et al. Design of robust controller in electrohydraulic load simulator[C]//Proceedings of 2006 International Conference on Machine Learning and Cybernetics. Piscataway, NJ: IEEE Press, 2006: 779-784.

[11] YAO J Y, JIAO Z X, YAO B, et al. Nonlinear adaptive robust force control of hydraulic load simulator[J]. Chinese Journal of Aeronautics, 2012, 25(5): 766-775.

[12] WANG C W, JIAO Z X, WU S, et al. A practical nonlinear robust control approach of electro-hydraulic load simulator[J]. Chinese Journal of Aeronautics, 2014, 27(3): 735-744.

[13] TRUONG D Q, AHN K K. Force control for hydraulic load simulator using self-tuning grey predictor-fuzzy PID[J]. Mechatronics, 2009, 19(2): 233-246.

[14] TRUONG D Q, AHN K K, SOO K J, et al. Application of fuzzy-PID controller in hydraulic load simulator[C]//Proceedings of 2007 International Conference on Mechatronics and Automation. Piscataway, NJ: IEEE Press, 2007: 3338-3343.

[15] PARK Y J, LEE S Y, CHO H S. A genetic algorithm-based fuzzy control of an electro-hydraulic fin position servo system[C]//Fuzzy Systems Conference Proceedings. Piscataway, NJ: IEEE Press, 1999: 1361-1366.

[16] WANG X, WANG S, WANG X. Electrical load simulator based on velocity-loop compensation and improved fuzzy-PID[C]//Proceedings of International Symposium on Industrial Electronics. Piscataway, NJ: IEEE Press, 2009: 238-243.

[17] 王新民, 劉衛國. 電液伺服加載的神經網絡內部反饋控制[J]. 航空學報, 2007, 28(3): 690-694. WANG X M, LIU W G. Neural-network internal feedback control for electro-hydraulic servo loading[J]. Acta Aeronautica et Astronautica Sinica, 2007, 28(3): 690-694 (in Chinese).

[18] 董傳陽. 民機液壓原理性驗證系統研究[D]. 杭州： 浙江大學, 2014. DONG C Y. Research on the hydraulic test system of the civil aircraft[D]. Hangzhou: Zhejiang University, 2014 (in Chinese) .

[19] 汪成文, 焦宗夏, 羅才瑾. 基于改進的速度同步控制的電液負載模擬器[J]. 航空學報, 2012, 33(9): 1717-1725. WANG C W, JIAO Z X, LUO C J. An improved velocity synchronization control on electro-hydraulic load simulator[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(9): 1717-1725 (in Chinese).

[20] YAO J Y, JIAO Z X, SHANG Y X, et al. Adaptive nonlinear optimal compensation control for electro-hydraulic load simulator[J]. Chinese Journal of Aeronautics, 2010, 23(6): 720-733.

[21] 吳振順. 液壓控制系統[M]. 北京: 高等教育出版社, 2008: 39-47. WU Z S. Hydraulic control system[M]. Beijing: High Education Press, 2008: 39-47 (in Chinese).

[22] 盧長耿, 李金良. 液壓控制系統的分析與設計[M]. 北京: 煤炭工業出版社, 1991: 121-124. LU C G, LI J L. Hydraulic control system[M]. Beijing: Coal Industry Press, 1991: 121-124 (in Chinese).

歐陽小平 男， 博士， 副教授， 碩士生導師。主要研究方向： 飛機液壓、 電液控制以及外骨骼機器人。

Tel: 0571-87952274

E-mail: ouyangxp@zju.edu.cn

Received： 2015-06-11； Revised： 2015-07-09； Accepted： 2015-10-13； Published online： 2015-10-15 09:01

URL： www.cnki.net/kcms/detail/11.1929.V.20151015.0901.002.html

Foundation items： National Natural Science Foundation of China (51275450， 51521064)； National Basic Research Program of China (2014CB046403)

*Corresponding author. Tel.： 0571-87952274 E-mail: ouyangxp@zju.edu.cn

Nonlinear optimal feedforward compensation controller forheavy load aviation load simulator

OUYANG Xiaoping1,*, LI Feng1, ZHU Ying2, YANG Shangbao2, YANG Huayong1

1.StateKeyLaboratoryofFluidPowerTransmissionandControl,ZhejiangUniversity,Hangzhou310027,China2.AviationKeyLaboratoryofScienceandTechnologyonAeroElectromechanicalSystemIntegration,Nanjing211100,China

Heavy load aviation load simulator is the ground simulation platform, which is used to simulate the real work load of the heavy-duty aircrafts such as C919 and Yun-20. A heavy-duty aviation load simulator is developed to achieve large load in limited space and the asymmetric cylinder is used as the actuator. In order to eliminate the influence of surplus force on the loading precision of the overloaded simulator, the influence of the bidirectional motions of the cylinder and the nonlinear flow gain coefficient of the servo valve for the feedforward compensation function are analyzed, and the nonlinear parameter estimation controller has been proposed. Meanwhile, the influence of dynamic parameters’ variation (such as acceleration) and static parameter error for eliminating the excessive force is analyzed, and the parameter optimal controller is developed. Both simulation and test results show that the performance of the developed feedforward compensation controller has been improved by more than 50% in the loading precision and the eliminating ability of the surplus force, compared to the traditional feedforward compensation controllers.

heavy load; load simulator; surplus force; nonlinear control; feedforward control

2015-06-11；退修日期：2015-07-09；錄用日期：2015-10-13； < class="emphasis_bold">網絡出版時間：

時間： 2015-10-15 09:01

www.cnki.net/kcms/detail/11.1929.V.20151015.0901.002.html

國家自然科學基金 (51275450， 51521064)； 國家“973”計劃 (2014CB046403)

.Tel.： 0571-87952274 E-mail: ouyangxp@zju.edu.cn

歐陽小平， 李鋒， 朱瑩， 等． 重載航空負載模擬器非線性最優前饋補償控制[J]． 航空學報, 2016, 37(2): 669-679. OUYANG X P, LI F, ZHU Y, et al. Nonlinear optimal feedforward compensation controller for heavy load aviation load simulator[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(2): 669-679.

http://hkxb.buaa.edu.cn hkxb@buaa.edu.cn

10.7527/S1000-6893.2015.0277

V242

：A

： 1000-6893(2016)02-0669-11

*