寬帶認知雷達低峰均比波形快速設計算法

唐波電子工程學院 504教研室， 合肥 230037

寬帶認知雷達低峰均比波形快速設計算法

唐波*
電子工程學院 504教研室， 合肥 230037

發射波形設計是寬帶認知雷達系統的關鍵技術。為了提高寬帶認知雷達系統對距離擴展目標的檢測性能，建立了目標檢測模型，分析了系統的檢測性能,在此基礎之上研究了基于最大輸出信干噪比(SINR)的低峰均比(PAR)波形設計算法。通過將原波形優化問題等效為接收權值與低峰均比波形的聯合優化問題，同時利用循環優化的思想，提出了一種低峰均比波形快速設計算法。相比于現有的梯度法以及凸優化算法，該算法所設計的恒模波形信干噪比與二者相當，但算法實現難度明顯變小，計算復雜度明顯降低。仿真結果證實了算法的有效性。

寬帶認知雷達； 距離擴展目標； 波形設計； 低峰均比(PAR)波形； 輸出信干噪比(SINR)； 循環優化

認知雷達是一種能夠感知和理解復雜電磁環境并在此基礎之上進行推理決策的新體制雷達系統[1-2]，是未來雷達系統的重要發展方向之一，近年來在國內外引起了巨大的關注。在認知雷達系統中，基于所感知的環境以及目標先驗知識設計發射波形是關鍵技術之一，有助于顯著地提高系統在復雜環境中的目標檢測、參數估計、跟蹤及識別性能[3-8]。

寬帶認知雷達是指發射大帶寬信號的認知雷達系統。寬帶雷達系統具有很高的距離分辨率，相比于窄帶雷達系統在目標成像以及識別等方面具有明顯的優勢[9]。與此同時，很多目標的尺寸超過了系統距離分辨單元的大小，不能再視作點目標，因此雷達視線方向上的多個強目標散射點回波就會分布在多個距離單元中。在寬帶雷達系統中，這類目標又被稱為距離擴展目標[10-11]。為了提高寬帶認知雷達系統對于距離擴展目標的檢測性能，系統設計發射波形時必須恰當地選擇優化準則。目前有2種準則可用于設計面向檢測性能最優的認知雷達發射波形。其中第1種優化準則引入了信息論中的相對熵概念[12-14]。當發射波形使得2類假設概率密度分布之間的相對熵達到最大時，則系統的檢測性能可以漸近地達到最優。第2種則基于最大化輸出信干噪比(SINR)來優化發射波形[15-19]。然而基于最大輸出信干噪比的現有波形設計方法大都僅考慮了波形的發射能量約束。在工程實際中，為了能夠使得雷達發射機工作在飽和狀態以便發揮其最大效能，同時為了避免放大器的非線性使得發射波形失真，通常要求雷達發射波形具有較低的峰均比(Peak-to-Average Power Ratio, PAR)或者恒定包絡[20-21]。因此實際系統設計發射波形時還必須考慮波形的峰均比約束。文獻[18]研究了基于最大化輸出信干噪比的寬帶認知雷達恒模波形設計方法，并提出了一種基于梯度下降法的波形優化算法。文獻[19]則利用半正定松弛(Semidefinite Relaxation, SDR)以及凸優化算法來設計使得輸出信干噪比最大的恒模波形。然而需要指出的是，梯度下降法以及凸優化算法只能設計恒模波形，不能設計任意峰均比約束下的雷達發射信號。此外，這2種算法運算量很大，難以設計長碼波形，進而影響寬帶認知雷達系統的最大作用距離。

本文建立了寬帶認知雷達的目標檢測模型，分析了系統的檢測概率和虛警概率。為了改善系統檢測性能，在此基礎之上研究了基于最大化輸出信干噪比的低峰均比波形設計算法，并提出了一種快速設計算法。該算法所設計的波形檢測性能與現有算法相當，但復雜度明顯降低。

1 信號模型

將寬帶認知雷達的發射信號記為s(t)。如果雷達天線波束內存在目標，如圖 1所示，雷達回波信號y(t)可以寫為

(1)

式中：τ1為距離雷達最近的目標散射點雙程延時；τ2為距離雷達最遠的目標散射點雙程延時，即目標徑向尺寸約為c(τ2-τ1)/2，c為光速；h(τ)為目標沖激響應；n(t)為外部干擾和接收機噪聲。為方便后續處理，對雷達回波信號y(t)進行模數轉換，將其變為數字信號，記為y，并注意到目標回波為沖激響應與發射信號的卷積，則不難得出

y=h?s+n

(2)

式中：h為長度為P的目標沖激矢量，P為目標散射點數，取決于目標徑向尺寸以及系統距離分辨率；s為經過離散化后的發射波形，長度為L；n為長度為(L+P-1)的噪聲及干擾矢量；?為卷積運算符。根據卷積運算定義，不難得出y又可寫為

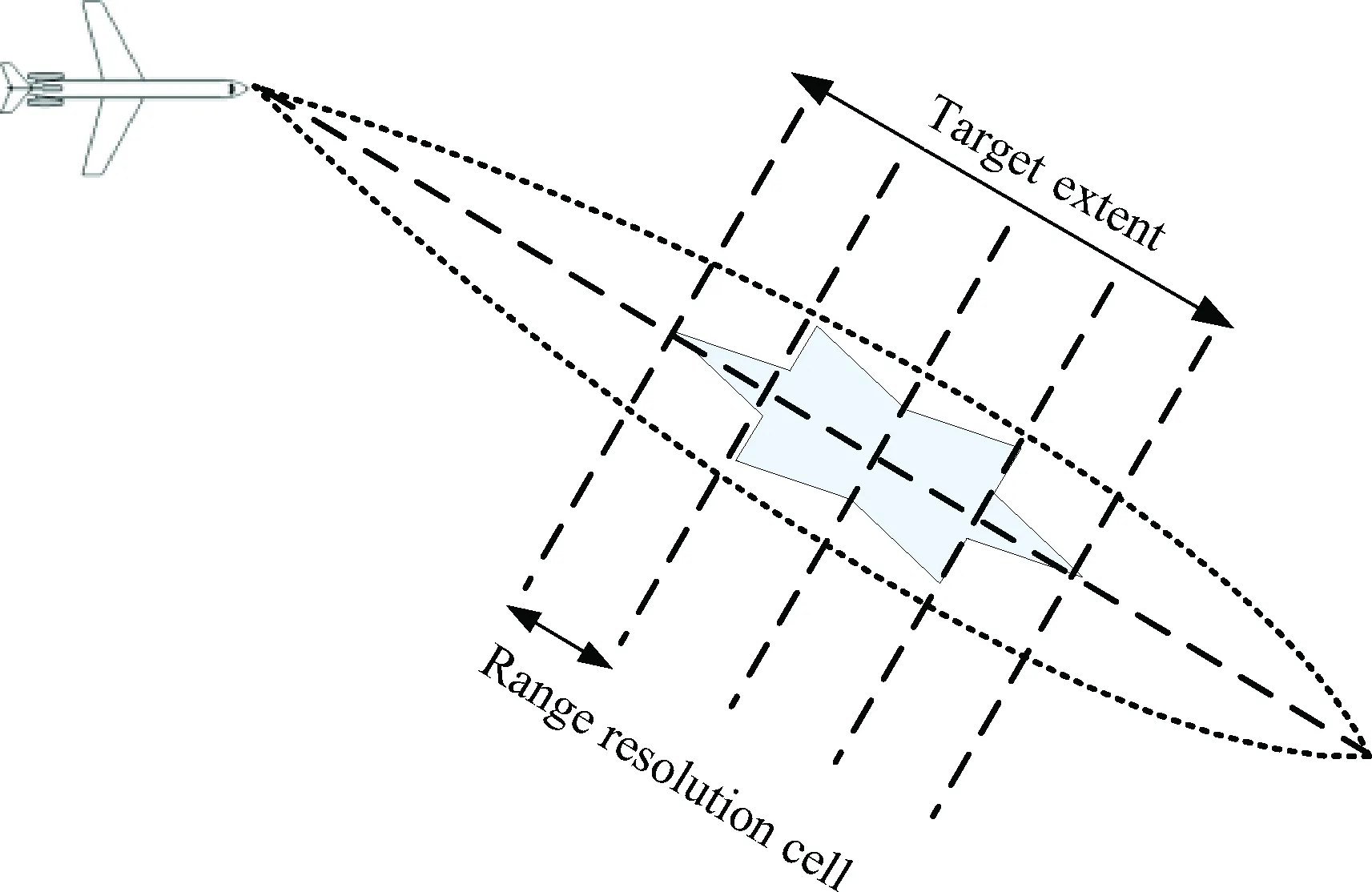
圖1 寬帶認知雷達目標檢測示意圖

Fig.1 Illustration of wideband cognitive radar detection

y=Hs+n

(3)

式中：H為(L+P-1)×L維卷積矩陣，其表達式為

(4)

當雷達天線波束內不存在目標時，則雷達回波信號可以寫為

y=n

(5)

基于以上結果，可以建立如下的二元假設檢驗模型用于檢測雷達回波中是否存在目標：

(6)

為簡單起見，假設目標沖激矢量h為確定矢量(非隨機)，n服從均值為0、協方差矩陣為R的復高斯分布，則目標回波y在兩類假設下的概率密度函數可以分別寫為

(7)

P(y|H1)=

(8)

利用似然比檢驗[22]，不難得出最優檢測器為

(9)

式中：T為門限。

在H0假設下，檢測器服從均值為0、方差為sHHHR-1Hs/2的高斯分布，因此虛警概率滿足

(10)

式中：erfc(·)為余補誤差函數，是x的單調遞減函數，其表達式為

(11)

在H1假設下，檢測器服從均值為sHHHR-1·Hs、方差為sHHHR-1Hs/2的高斯分布，因此檢測概率為

(12)

利用式(10)，目標檢測概率可以進一步寫成

(13)

式中：erfc-1(·)為余補誤差函數的逆函數。由于erfc(x)隨著x單調遞減，因此目標檢測概率PD是輸出信干噪比

SINR=sHHHR-1Hs

(14)

的單調遞增函數，故而輸出信干噪比的大小直接關乎系統檢測性能的優劣。接下來討論如何設計波形s使得輸出信干噪比最大。

實際系統中雷達發射信號的能量總是有限的。不失一般性，假設發射信號的能量不超過L，即

sHs≤L

(15)

在認知雷達系統的波形設計中，假設已有目標和環境的先驗知識[23]，因此能量約束下的波形設計問題可以建模為

s.t.sHs≤L

(16)

很明顯，當雷達發射信號僅受限于發射能量時，最優發射波形為

s=(HHR-1H)

(17)

由于工程實際需要，設計發射波形時需要考慮雷達波形的低峰均比約束，其中峰均比定義為

(18)

式中：s(l)為波形s的第l個采樣。

考慮峰均比約束后，寬帶認知雷達的發射波形設計可以建模為如下的優化問題：

s.t. PAR(s)≤γ,sHs≤L

(19)

不難發現1≤PAR(s)≤L。當γ=1時，s為恒包絡信號；當γ=L時，則峰均比約束為冗余約束，上述優化問題的解為式(17)。由于峰均比約束高度非凸，因此很難求得式(19)的全局最優解。

2 波形快速設計算法

為了能夠設計碼長較長的低峰均比發射波形并減小波形設計運算量，下面給出一種快速設計方法。首先證明式(19)中的優化問題與式(20)等價：

s.t. PAR(s)≤γ,sHs≤L

(20)

式(20)是一個發射波形s與接收權值w的聯合優化問題，但約束條件只與發射波形s有關，而與權值w無關。不難看出式(20)存在無窮多解，這是因為如果(wopt, sopt)是式(20)的可行解，則(αwopt, sopt)也是可行解，即權值w的尺度變化不影響目標函數的取值。此外，當波形s固定時，最優權值w可以通過如下優化問題獲得:

(21)

將Hs等效為導引矢量，則式(21)與陣列信號處理中經典的最小方差無失真響應(MinimumVarianceDistortlessResponse，MVDR)[24]是等價的，即式(21)等價于

s.t.wHHs=1

(22)

可以定義如下拉格朗日乘子函數求解式(22)中的優化問題:

F(λ)=wHRw+λ(wHHs-1)

(23)

式中：λ為拉格朗日乘子。

將式(23)對w求導并令求導結果為0，并注意到權值w的尺度變化不影響目標函數的取值，可得式(21)的最優解為

wopt=R-1Hs

(24)

且目標函數最大值為sHHHR-1Hs。因此通過一步優化，可以將式(20)中的聯合優化問題轉化為式(19)中的優化問題，故而式(20)與式(19)等價。

可以使用循環優化方法[21,25]求解式(20)中的聯合優化問題，即每一次迭代中，將其分解為兩個相對獨立的優化問題：① 固定波形s(i)優化權值w(i)；② 固定權值w(i)優化低峰均比波形s(i+1)。很明顯，第①步優化結果由式(24)給出。接下來討論第②步優化的求解方法。在第②步優化中，需要求解如下優化問題：

s.t. PAR(s)≤γ,sHs≤L

(25)

注意到式(25)目標函數的分母與波形s無關，故可以將其簡化為

s.t. PAR(s)≤γ,sHs≤L

(26)

記v(i)=HHw(i)。如果γ=1(恒定包絡約束)，則利用基本代數不等式，可得出

(27)

當且僅當

s(l)=exp(j∠v(i)(l))

(28)

時不等號成立。

式中：v(i)(l)為v(i)的第l個元素；∠v(i)(l)為v(i)(l)的相位。即最優解為

s(i+1)=exp(j∠v(i))

(29)

如果γ≠1，則可證明式(26)與下面的優化問題等價：

s.t. PAR(s)≤γ,sHs≤L

(30)

很明顯

(31)

將式(30)的最優解記作s(i+1)，并記

(32)

如果φ0≠0，則

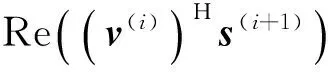
以及

(33)

與s(i+1)的最優性相矛盾，因此式(30)的最優解必然滿足

(34)

故而式(26)與式(30)等價。此時便可以利用文獻[26]中的最近鄰迭代算法求得式(30)的最優解。

綜上，寬帶認知雷達系統的低峰均比波形設計算法可以總結如下：

步驟1 i=0，初始化波形s(i)。

步驟2 i=i+1，利用式(24)計算w(i)以及利用最近鄰迭代得到s(i+1)，計算輸出信干噪比SINR(i+1)。

注意到v(i)=HHw(i)=HHR-1Hs(i)，因此如果能夠事先計算好HHR-1H，則可以進一步減少本算法的運算量。

與文獻[18]中的梯度下降法以及文獻[19]中的凸優化算法相比，本算法實現簡單，且能夠設計任意峰均比約束下的雷達波形。在設計恒模波形時，本算法每一步迭代的運算量可以控制在O(L2)的量級，遠低于梯度法O(L3)的運算量以及凸優化算法O(L4.5)的運算量，且對存儲的要求很低，能夠設計很長的碼長。

3 數值仿真與分析

為驗證算法的有效性，考慮信號帶寬為100MHz的寬帶認知雷達系統，波形采樣后的長度L=50，目標占據的距離單元數P=20，目標沖激響應如圖2所示。干擾及接收機噪聲n采用一階自回歸(AR)過程建模，AR過程的相關系數ρ=0.9。

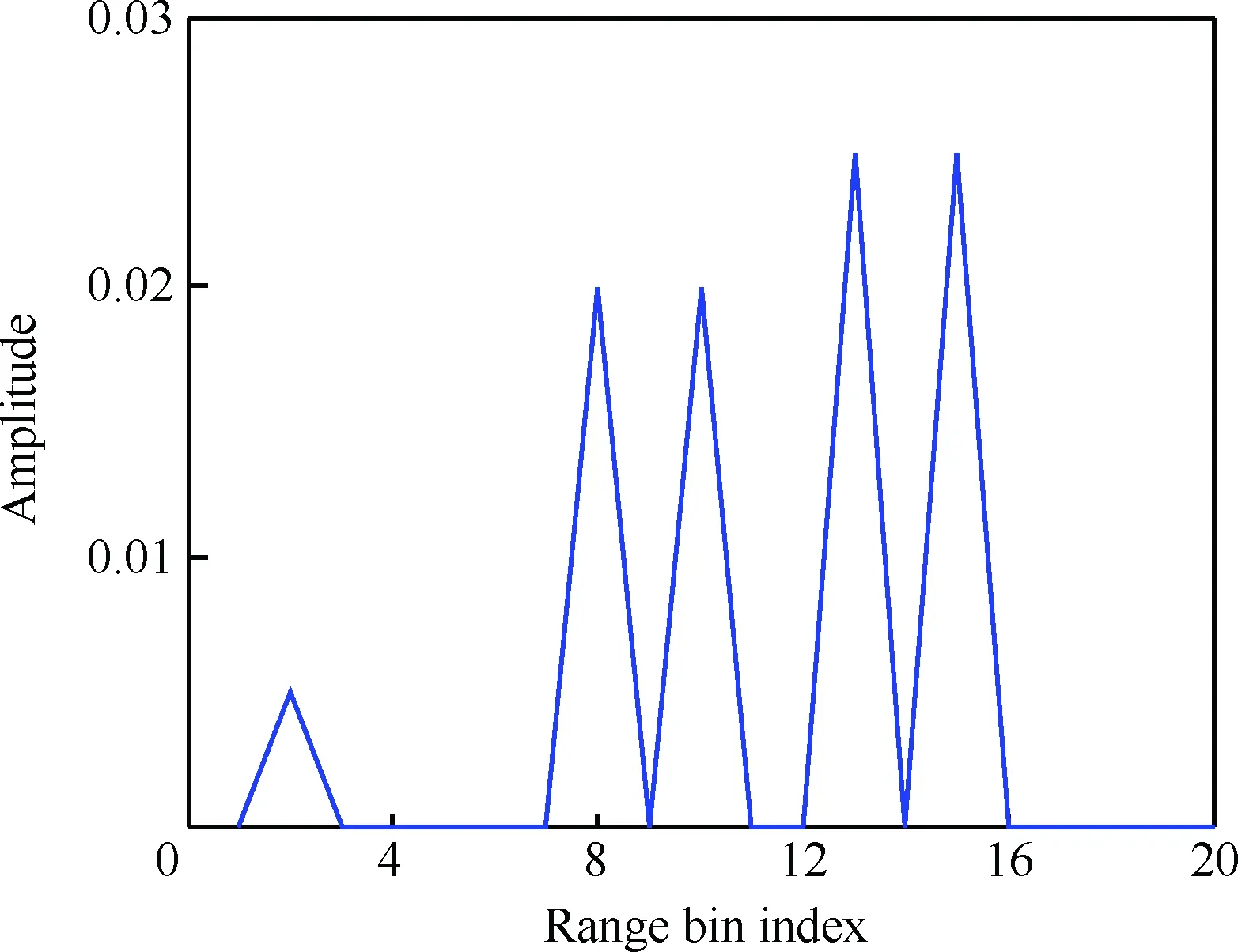
圖2 目標沖激響應

Fig.2 Target impulse response

圖3為本文算法所設計的波形信干噪比隨著迭代次數的變化曲線，其中采用隨機生成的偽正交相位編碼信號作為算法的初始值，迭代截止門限ε=10-6。可以看出，本文算法收斂很快，收斂后輸出信干噪比約為6.16dB，接近于能量約束下的最大信干噪比(約為6.41dB)。而采用相同帶寬的線性調頻(LinearFrequencyModulation,LFM)信號，輸出信干噪比僅為0dB。

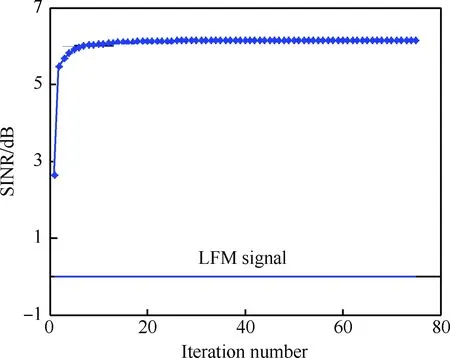
圖3 本文算法信干噪比(SINR)隨著迭代次數的變化曲線

Fig.3 Convergence of SINR of proposed algorithm against iteration number

為了比較本文算法與文獻[18-19]所提的梯度法以及凸優化算法，采用與圖3相同的仿真參數，圖4以及圖5分別給出了100次獨立蒙特卡羅實驗下3種算法的計算耗時(Inteli5-4200MCPU，4G內存)及輸出信干噪比直方分布圖，其中本文算法平均用時僅需0.007 5s，平均信干噪比為6.10dB，梯度法平均用時0.195s，平均信干噪比為6.10dB，凸優化算法平均用時0.795s，平均信干噪比為6.27dB。可以看出，本文算法與梯度法的性能相當，稍劣于凸優化算法，但是算法耗時遠遠低于凸優化算法。

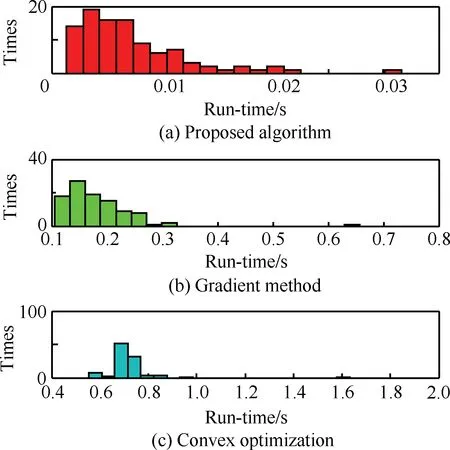
圖4 3種算法用時比較

Fig.4 Comparison of run-time of three algorithms

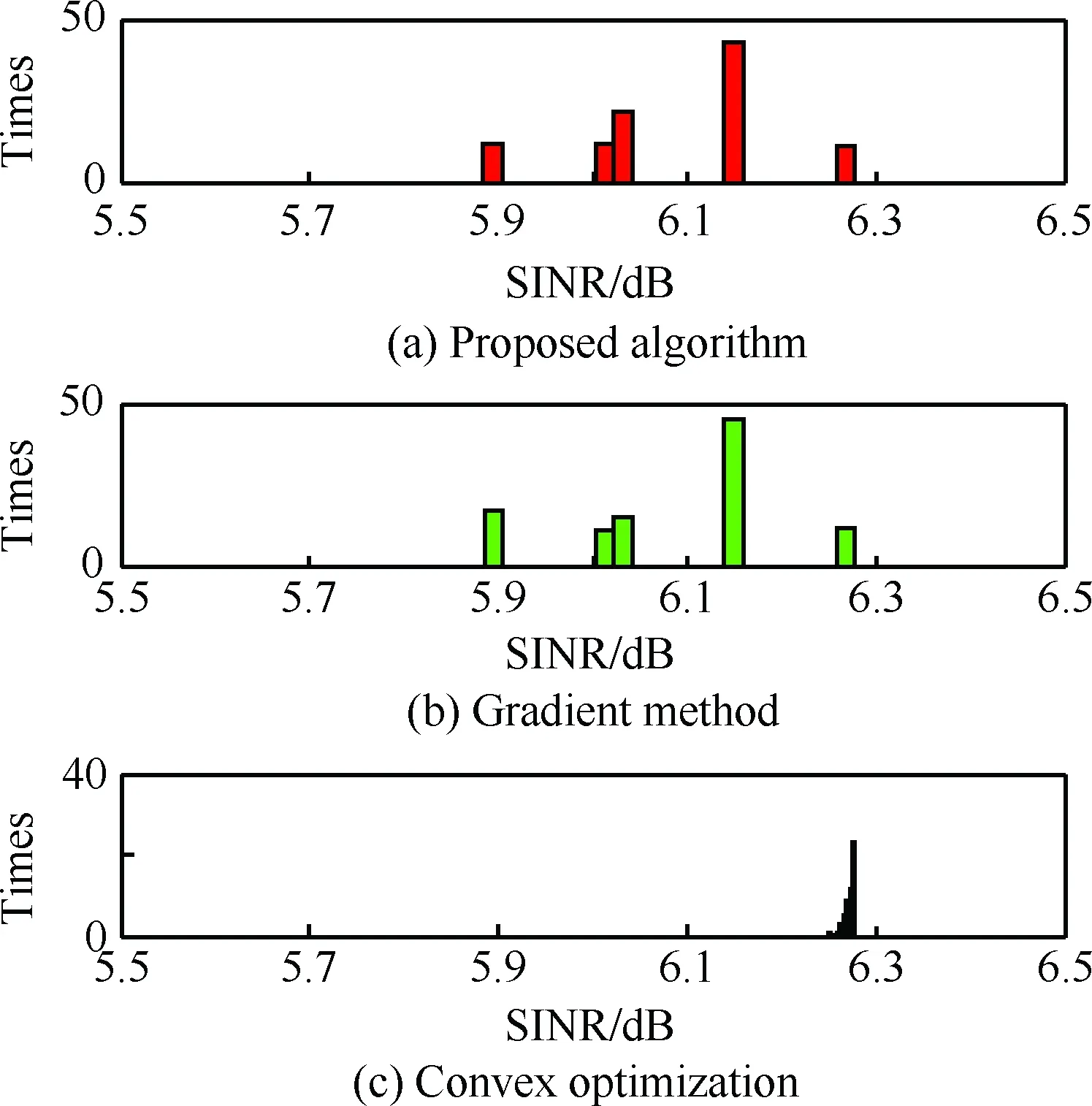
圖5 3種算法輸出信干噪比比較

Fig.5 SINR comparison of three algorithms

另外，在該計算機上凸優化算法所設計的波形長度L不能超過300，當碼長L超過500時梯度法難以收斂，而對于本文算法，僅需要2s左右的時間就能設計碼長超過1 000的恒模波形。

最后，圖6為不同峰均比約束下所設計的波形信干噪比，可以看出，當峰均比增加時，由于式(19)中的可行解集合區域更大，因此波形的輸出信干噪比會有所增加。同時圖中結果也表明，當γ=2時，所設計波形的輸出信干噪比非常接近能量約束下的最大輸出信干噪比。

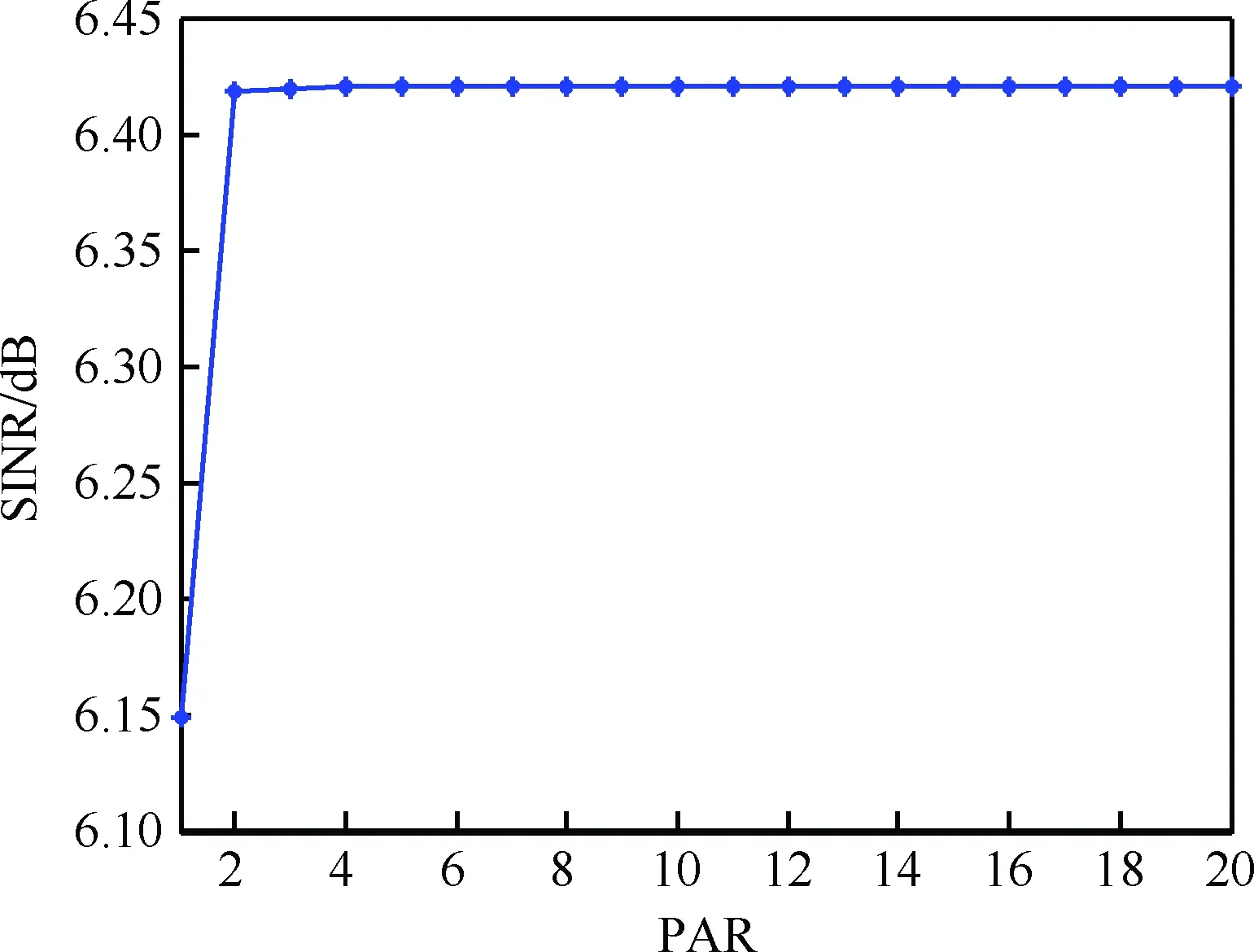
圖6 輸出信干噪比與峰均比的關系

Fig.6 Relationship between SINR and PAR

4 結 論

建立了寬帶認知雷達的信號模型，分析了系統的檢測概率和虛警概率，研究了任意峰均比約束下基于最大輸出信干噪比的波形設計問題。通過將原有波形優化問題等價為權值以及波形的聯合優化問題，并利用循環優化的思想，提出了一種能夠用于改善距離擴展目標檢測性能的低峰均比波形快速設計算法。相比于梯度法以及凸優化算法，本文算法所設計的恒模波形與它們性能相當，但是實現難度明顯更小，計算復雜度明顯降低，有更強的實用性。

[1] HAYKIN S. Cognitive radar: A way of the future[J]. IEEE Signal Processing Magazine, 2006, 23(1): 30-40.

[2] GUERCI J R. Cognitive radar: The knowledge-aided fully adaptive approach[M]. Norwood, MA: Artech House, 2010: 13-30.

[3] HE H, LI J, STOICA P. Waveform design for active sensing systems: A computational approach[M]. Cambridge: Cambridge University Press, 2012: 1-14.

[4] SOLTANALIAN M, TANG B, LI J, et al. Joint design of the receive filter and transmit sequence for active sensing[J]. IEEE Signal Processing Letters, 2013, 20(5): 423-426.

[5] AUBRY A, DE MAIO A, PIEZZO M, et al. Cognitive design of the receive filter and transmitted phase code in reverberating environment[J]. IET Radar, Sonar & Navigation, 2012, 6(9): 822-833.

[6] AUBRY A, DE MAIO A, JIANG B, et al. Ambiguity function shaping for cognitive radar via complex quartic optimization[J]. IEEE Transactions on Signal Processing, 2013, 61(22): 5603-5619.

[7] TANG B, TANG J, PENG Y. Waveform optimization for MIMO radar in colored noise: Further results for estimation-oriented criteria[J]. IEEE Transactions on Signal Processing, 2012, 60(3): 1517-1522.

[8] WANG H, SHI L, WANG Y, et al. A novel target detection approach based on adaptive radar waveform design[J]. Chinese Journal of Aeronautics, 2013, 26(1): 194-200.

[9] WEHNER D R. High resolution radar[M]. Norwood, MA: Artech House, 1987: 1-10.

[10] CARRETERO-MOYA J, DE MAIO A, GISMERO-MENOYO J, et al. Experimental performance analysis of distributed target coherent radar detectors[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(3): 2216-2238.

[11] HE Y, JIAN T, SU F, et al. Novel range-spread target detectors in non-Gaussian clutter[J]. IEEE Transactions on Aerospace and Electronic Systems, 2010, 46(3): 1312-1328.

[12] COVER T M, THOMAS J A. Elements of information theory[M]. New York: John Wiley & Sons, 2012: 380-384.

[13] KAY S. Waveform design for multistatic radar detection[J]. IEEE Transactions on Aerospace and Electronic Systems, 2009, 45(3): 1153-1166.

[14] TANG B, TANG J, PENG Y. MIMO radar waveform design in colored noise based on information theory[J]. IEEE Transactions on Signal Processing, 2010, 58(9): 4684-4697.

[15] PILLAI S U, OH H S, YOULA D C, et al. Optimal transmit-receiver design in the presence of signal-dependent interference and channel noise[J]. IEEE Transactions on Information Theory, 2000, 46(2): 577-584.

[16] LI J, GUERCI J R, XU L Z. Signal waveform’s optimal-under-restriction design for active sensing[J]. IEEE Signal Processing Letters, 2006, 13(9): 565-568.

[17] BERGIN J S, TECHAU P M, DON CARLOS J E, et al. Radar waveform optimization for colored noise mitigation[C]//IEEE International Radar Conference. Piscataway, NJ: IEEE Press, 2005: 149-154.

[18] ZHANG J, ZHU X, WANG H. Adaptive radar phase-coded waveform design[J]. Electronics Letters, 2009, 45(20): 1052-1053.

[19] 魏軼旻, 孟華東, 毛滔, 等. 基于凸優化方法的認知雷達波形設計[J]. 現代雷達, 2012, 34(3): 18-21. WEI Y M, MENG H D, MAO T, et al. Radar phase-coded waveform design for extended target detection by convex optimization[J]. Modern Radar, 2012, 34(3): 18-21 (in Chinese).

[20] DE MAIO A, HUANG Y W, PIEZZO M, et al. Design of optimized radar codes with a peak to average power ratio constraint[J]. IEEE Transactions on Signal Processing, 2011, 59(6): 2683-2697.

[21] 唐波, 張玉, 李科, 等. 雜波中MIMO雷達恒模波形及接收機聯合優化算法研究[J]. 電子學報, 2014, 42(9): 1705-1711. TANG B, ZHANG Y, LI K, et al. Joint constant-envelope waveform and receiver design for MIMO radar in the presence of clutter[J]. Acta Electronic Sinica, 2014, 42(9): 1705-1711 (in Chinese).

[22] KAY S M. Fundamentals of statistical signal processing, VOL. II: Detection theory[M]. Upper Saddle River, NJ: Prentice Hall, 1998: 60-74.

[23] 唐波, 張玉, 李科. 基于先驗知識及其定量評估的自適應雜波抑制研究 [J]. 航空學報, 2013, 34(5): 1174-1180. TANG B, ZHANG Y, LI K. Adaptive clutter suppression based on prior knowledge and its evaluation[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(5): 1174-1180 (in Chinese).

[24] VAN TREES H L. Optimum array processing [M]. New York: John Wiley & Sons, 2002: 440-446.

[25] STOICA P, SELéN Y. Cyclic minimizers, majorization techniques, and the expectation-maximization algorithm: A refresher[J]. IEEE Signal Processing Magazine, 2004, 21(1): 112-114.

[26] TROPP J A, DHILLON I S, HEATH R W, et al. Designing structured tight frames via an alternating projection method[J]. IEEE Transactions on Information Theory, 2005, 51(1): 188-209.

唐波 男， 博士， 講師。主要研究方向： 自適應雷達信號處理及波形設計。

Tel: 0551-65927461

E-mail: tangbo06@gmail.com

Received： 2015-01-27； Revised： 2015-04-23； Accepted： 2015-05-05； Published online： 2015-05-25 09:54

URL： www.cnki.net/kcms/detail/11.1929.V.20150525.0954.003.html

Foundation items： National Natural Science Foundation of China (61201379); Anhui Provincial Natural Science Foundation (1208085QF103， 1608085MF123)

*Corresponding author. Tel.： 0551-65927461 E-mail: tangbo06@gmail.com

Efficient design algorithm of low PAR waveform for widebandcognitive radar

TANG Bo*

Lab504,ElectronicEngineeringInstitute,Hefei230037,China

Transmit waveform design is a key technique in wideband cognitive radar. In order to improve the detection performance of range spread targets for wideband cognitive radar system, a target detection model is established. Then the detection performance associated with the signal model is analyzed. Afterward, the design method of low peak-to-average power ratio (PAR) waveform is studied based on maximizing signal-to-interference-plus-noise ratio (SINR). In the development of the proposed algorithm, the original waveform optimization problem is tackled by considering its equivalent form, which is a joint design problem of low PAR waveform and receiving filter. Based on the idea of cyclic optimization, an efficient design method for low PAR waveform is proposed. The output SINR of the designed constant envelope waveform is similar to that of the existing gradient descent method and convex optimization method. However, the proposed algorithm is much easier to implement and has considerably lower computational complexity. The effectiveness of the proposed algorithm is verified by the numerical simulations.

wideband cognitive radar; range spread target; waveform design; low peak to average power ratio (PAR) waveform; signal to interference plus noise ratio (SINR); cyclic optimization

2015-01-27；退修日期：2015-04-23；錄用日期：2015-05-05； < class="emphasis_bold">網絡出版時間：

時間： 2015-05-25 09:54

www.cnki.net/kcms/detail/11.1929.V.20150525.0954.003.html

國家自然科學基金 (61201379)； 安徽省自然科學基金 (1208085QF103， 1608085MF123)

.Tel.： 0551-65927461 E-mail: tangbo06@gmail.com

唐波． 寬帶認知雷達低峰均比波形快速設計算法[J]． 航空學報, 2016, 37(2): 688-694. TANG B. Efficient design algorithm of low PAR waveform for wideband cognitive radar[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(2): 688-694.

http://hkxb.buaa.edu.cn hkxb@buaa.edu.cn

10.7527/S1000-6893.2015.0125

V243.2；TN959.73

： A

： 1000-6893(2016)02-0688-07

*