環環相扣 重點突出
高金盔

【摘 要】本文針對技工學校《工程力學》中《拉伸與壓縮》這一部分的基本概念、方法的教學的教學體會。
【關鍵詞】技工學校;工程力學;拉伸與壓縮;教學
工程力學是一門技術基礎學科,內容涉及力學中的理論力學和材料力學兩個分支。在材料力學中分拉壓、剪切、扭轉、彎曲四種基本變形的闡述,其中軸向拉壓問題是材料力學中最簡單部分,但在這一章中將介紹許多重要的基本概念和基本解題方法,這些問題的掌握對學好材料力學十分重要,可以說是材料力學的基礎部分和最基本內容。以下是我對《拉伸與壓縮》一章的教學體會。
第一,從拉壓變形受力分析特點自然引出內力概念(這是本章重點及難點所在)。
內力概念較難理解,因此這部分要詳細講解,在闡述拉壓部分的受力特點是作用在桿件兩端的外力等值、反向時重點強調其作用線與桿件軸線重合。作用在兩端的外力若是分布力要簡化成集中力即合力。當構件在外力作用下將引起內部一部分對另一部分的作用力——內力。內力又分兩種情況,當構件不受外力時,組成物體的分子間存在著吸引力和排斥力,它們之間相互平衡保持了分子之間的相對位置不變。這樣就維持了固體的形狀,這種內力在物理上稱為分子結合力。但它不是材料力學的研究對象。另外一種情況是當物體受到外力作用時,由于物體的變形改變了物體分子之間的距離從而破壞了原來內部分子之間的平衡力。為了使物體內部分子之間作用力達到新的平衡,在原有分子之間結合力基礎上必定要改變。這個因外力作用而產生的內力該變量即內力增量才是材料力學的研究對象,也就是材料力學中真正意義的內力。它有如下特點:內力是隨變形而產生的;內力總是趨向保持物體原有的形狀而抵抗變形;當內力抵抗不了由外力產生的桿件變形的影響時,桿件就要破壞。所以內力是與材料強度密切相關的。
求內力可用教材中講述的應用靜力學平衡方程的截面法。在講截面法求內力的過程中要講清楚隨外力作用位置的不同各截面上的內力也不同。因此內力不可以離開截面,內力必須指明是哪一截面上的內力,否則沒有意義。對于同一截面所分兩部分因取研究對象不同,得到的內力的方向相反,正負號的規定則以受內力而是桿件產生的變形效果來規定的。受拉為正,受壓為負。因拉壓變形受力特點中外力活合外力與桿件的軸線重合,故內力也與桿件的軸線重合,因此把拉壓時內力稱為軸力。
截面法求內力的方法和步驟應不斷加強,并重點掌握,因為后面三種基本變形求內力的剪力、彎矩和扭矩的方法類似,都采用“截開、代替、平衡”的方法。
(1)截開:將桿件在欲求內力的截面處假想地切開,取其中一部分為研究對象,畫出該部分所受的外力。
(2)代替:用截面上的內力來代替去掉部分對選取部分的作用。
(3)平衡:列出選取部分的靜力學平衡方程,確定未知力的大小和方向。
在用截面法求內力時應注意:
(1)當求解存在多個外力作用的桿件的內力時,切記主管判斷而誤將截面附近作用的外力作該截面上的內力。
(2)在兩個軸向外力之間任取截面時,不要在外力作用點切去,因為在外力作用點處的截面上其內力是不確定值。
(3)軸力的大小等于截面一側(左或右)所以外力的代數和。
(4)力的可傳遞性原理在材料力學中已不適用。
第二,內力只能說明值的大小,分布的密集程度怎樣還要引出應力的概念。
應力是表示內力的密集度,不能簡單地說應力是單位面積上的內力。因為應力概念不能等同于平均應力,應力在截面上一般情況下并非平均分布,故截面上某點的應力值與在改點附近所取面積的大小有關,只有當應力在截面上均勻分布的情況下,平均應力才能代表截面上任意點的應力。
在承受軸向拉壓的桿件中,通過試驗觀察及平面假設已經得出結論,應力在截面上是平均分布的。因此在這種情況下用單位面積上的內力求出的平均應力就是截面上任意點的應力,也就是最大應力。
軸向拉壓桿件橫截面上的應力只能有軸力,它是與截面垂直的。故截面上只有正應力,最大正應力可用公式:σ=Nmax/A求得,式中:σmax—最大正應力,Nmax—桿件內最大軸力,A—橫截面積
第三,胡克定律(很重要,但較易理解)。
胡克定律在材料力學中由實驗總結出來,定律有兩種表達式(1)ΔL=(N*L)/(E*A)(2)σ=E*ε這里E從數學上來講是比例常數,但它的力學意義為材料抗拉壓的彈性模量,由實驗測得,大小只與材料有關,與形狀無關。一般來講同一種材料的彈性模量“E”是常數。第一種表達式ΔL=(N*L)/(E*A)用來求絕對變形量,為建立剛度條件打基礎,ΔL<[ΔL]若沿桿件軸線方向不是常數,求ΔL要分段總和。第二種表達式σ=E*ε可用來應力分析,如通過儀器可以求出桿件受力后的線應變ε,一般制造桿件材料的彈性模量E是已知的,則用σ=E*ε式很容易求出此時桿件內正應力σ值,以此來檢驗桿件強度,或核對理論計算的正確性。若已知E和ε,在后面強度計算中亦可應用σ=E*ε計算出工作應力進行強度校核σ=E*ε<[σ]。
在講解胡克定律時,為調動學生積極性和培養學生探究精神可采取如下措施:
(1)講述胡克生平和科學貢獻,與力學泰斗牛頓的糾葛。
(2)根據教學條件,準備彈簧、測力器等器材簡單驗證胡克定律。
第四,由力學性能試驗引出幾種力學性能指標,進行強度計算問題(此為應用部分,應重點掌握)。
材料力學性能是通過各種試驗方法測定的。技校學生主要應了解萬能試驗機的性能及通過低碳鋼的拉伸試驗,如何求出拉伸圖和拉伸圖上的各種特征點代表的機械性能。比如比例極限σpσs,σb延伸率,斷面收縮率Ψ等。
工程上使用的各種構建的破壞應力是指試件不能正常工作的應力,與材料的破壞應力不完全相同,故由塑性材料制成的構件,材料的屈服極限則認為是危險應力σ0=σs,由脆性材料制成的桿件,其破壞應力可以是強度極限σ0=σb。
構件或者零件在荷載作用下,構件內產生的實際應力稱為工作應力σ=N/A,而桿件內工作應力的最大允許值稱為許用應力,用[σ]表示,[σ]=σ0/n式中n為安全系數。
利用安全系數的目的是為了使桿件內有一定的強度儲備,確保桿件的安全。但并不是安全系數越大越好,相反,在保證安全的前提下,安全系數越小越好。選擇安全系數對國民經濟有重要意義,節約原材料以達到既安全又經濟的目的,這是材料試驗的主要意義之一。
綜上可知,軸向拉壓構件的最大工作應力,只有小于或等于材料的需用應力才是安全的。強度條件為:
σmax=Nmax/A<[σ]
式中σmax—最大工作應力
Nmax—最大軸力
A—危險截面面積
[σ]—材料的許用應力
強度條件可以解決三類問題:校核強度,設計截面尺寸及安全載荷。但此三類運算并非只能用此條件關系式。如前述胡克定律σ=E*ε亦可求出材料的工作應力。σ=E*ε<[σ]也可進行強度校核,但σmax=Nmax/A<[σ]是最基本最常見的強度條件式。
應用強度條件解決工程上某些問題,是拉壓變形一章所要達到的主要目的。學生第一次接觸強度條件,很好地掌握這部分內容對學習材料力學后部分知識也有深遠影響。
第五,應力集中和冷作硬化在教材中為選學內容,而對于技校焊工專業來講這兩個概念經常用到,但后續課程大都是應用,沒有系統講解。因此在此應對兩種現象的機理做出重點分析。
1)應力集中
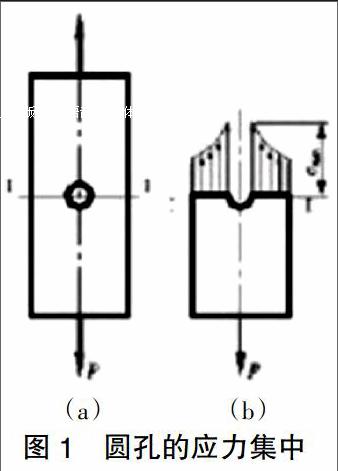
(1)應力集中:因桿件外形突然變化而引起局部應力急劇增大的現象,稱為應力集中。
出現應力集中的原因:構件截面尺寸的突然變化。經常出現在切口、開槽、螺紋、油孔和臺肩等部位。
應力集中系數α=σmax/σm,反映應力集中的程度,其中σmax為截面上的最大應力,σm同一截面上的平均應力。
應力集中對桿件強度的影響。在靜荷載(荷載從零緩慢增加到一定值后保持不變)作用下,塑性性材料可以不考慮應力集中的影響,因為塑性材料有屈服現象,而脆性材料必須考慮應力集中。在動荷載(荷載隨時間變化)作用下,不論是塑性材料還是脆性材料,都應該考慮應力集中對構件強度的影響,它往往是構件破壞的根源。
2)冷作硬化:金屬材料在常溫或再結晶溫度以下的加工產生強烈的塑性變形,使晶格扭曲、畸變,晶粒產生剪切、滑移,晶粒被拉長,這些都會使表面層金屬的硬度增加,減少表面層金屬變形的塑性,稱為冷作硬化。金屬在冷態塑性變形中,使金屬的強化指標,如屈服點、硬度等提高,塑性指標如伸長率降低的現象稱為冷作硬化。
以上是我在講解《拉伸與壓縮》這一章知識總的思路及體會,我認為按照這一思路及所列知識點進行講解可以將這一章的重點、難點講清、講透,并為后續內容的學習打下良好的基礎。
【參考文獻】
[1]鐘少華.工程力學[M].北京:中國勞動社會保障出版社,2012.
[責任編輯:王楠]

