高職學生綜合素質評價的數(shù)學模型

謝紅軍 劉子賢

(1.四川托普信息技術職業(yè)學院 四川 成都 611743;2.四川省犍為一中 四川 犍為 614400)

高職學生綜合素質評價的數(shù)學模型

謝紅軍1劉子賢2

(1.四川托普信息技術職業(yè)學院 四川 成都 611743;2.四川省犍為一中 四川 犍為 614400)

應試教育轉變?yōu)樗刭|教育，需改進原有的考試評價方法，建立科學的高職學生綜合素質評價指標體系。在對高職學生的綜合素質結構進行分析并廣泛征求專家意見的基礎上，利用層次分析法，建立了一套高職學生的綜合素質評價指標體系和評價方法，以全面反映高職學生的綜合素質水平。

綜合素質；評價體系；層次分析；數(shù)學模型

1 引言

教育的目的是讓學生的全面發(fā)展，提高學生的綜合素質，并將學生所學知識轉化為學生的綜合素質。鑒于此，我們在提高學生綜合素質的過程中必須抓住它的難點和本質，深化學生綜合素質評價改革，實現(xiàn)素質教育真正融入整個教育過程中。學生也需要根據(jù)科學評價的反饋信息來優(yōu)化、調(diào)整學習和成長發(fā)展策略，在自我完善和改進中得到提升。因此，在實際應用過程中需要建立能滿足科學、動態(tài)、可量化的評價體系與方法。

2 高職學生綜合素質評價的層次結構

2.1 高職學生綜合素質評價指標的設計原則

(1)全面性原則：各指標應充分反映高職學生綜合素質的內(nèi)涵，系統(tǒng)而準確地把握其實質。(2)主要性原則：各指標應反映高職學生綜合素質的主要特征。(3)可操作性原則：各指標中的指標應能獲得明確的量化結果或者有量化手段與之相對應。(4)可參照性原則：被選取的指標能反映高職學生發(fā)展的共性，具有普遍性。

2.2 高職學生綜合素質評價體系

為了科學地評價學生的綜合素質，必須明確國家教育目標導向、學校培養(yǎng)方向以及辦學理念，按照各類學校的特點，建立符合大部分高職類學生綜合素質評價的合理指標體系。由美國學者T．L．Saaty提出的層次分析法把人的思維系統(tǒng)化、數(shù)量化，并用數(shù)學方法為分析、評價、預報或決策提供更科學的依據(jù)。應用該方法建立評價高職類學生綜合素質的層次結構模型，如下圖所示。

第三層下還可增設多層，它們可以為課程或研究課題，應視不同的學校和專業(yè)各有差異。對不同學校而言，層次結構的分支也應適當調(diào)整，建立符合自身發(fā)展特點的評價體系。

2.3 評價高職學生綜合素質水平的應用示例

評價四川托普信息技術職業(yè)學院某系二年級一個班45名學生中某學生(學號為143030101)一個學期的綜合素質，具體過程如下:

2.3.1 確定成對比較矩陣

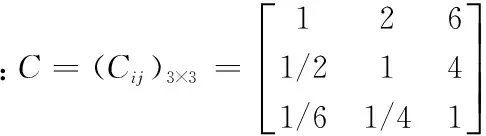
2.3.2 矩陣的權向量及一致性檢驗

比較矩陣C，顯然滿足一致性檢驗(階數(shù)為3)，算得出它的最大特征值為：ans0=3.01，利用一致性檢驗指標CI=0.005和隨機一致性檢驗指標RI算出一致性檢驗比率CR=CI/RI=0.0086<0.1，顯而易見C通過了一致性檢驗。容易得出矩陣C的權系數(shù),并且與之相應的權向量為：B1=(B11,B12,B13)=(0.59，0.32，0.09) 同理，可以得出同一層中其他因素對上層因素的影響權向量分別有：

(1)第二層對第一層的影響，它的最大特征值為：ans1=4.24；相應的權向量為：

B=(B1,B2，B3,B4)T=(0.35，0.40，0.13，0.12)T，

(2)第三層中關于德育素質的影響因素，相應的權向量為：

B2=(B21,B22,B23,B24)T=(0.30，0.25，0.29，0.16)T；

(3)第三層中關于文體素質的影響因素，相應的權向量為：

B3=(B31,B32,B33)T=(0.38，0.39，0.23)T；

(4)第三層中關于人文素質的影響因素，相應的權向量為：

B4=(B41,B42,B43)T=(0.38，0.35，0.27)T；

2.3.3 綜合評價公式及應用

上述計算給出了各因素之間影響的定量標準，則高職學生綜合素質評價模型為：Y=0.35(0.59X1+0.32X2+0.09X3)+0.40(0.30X4+0.25X5+0.29X6+0.16X7)+0.13(0.38X8+0.39X9+0.23X10)+0.12(0.38X11+0.35X12+0.27X13) 其中Xi,表示第三層各因素在專家評價下的最終得分，i=1,2,……，13。

本文應用專家評分的方法，采用十分制分別對第三層各因素進行評分。同時為了減小誤差，假設專家由多人組成，分別對層次結構中每一個因素如(B11)打分，先去掉一個最高分和一個最低分，然后對剩下的專家評分結果求平均值即為該因素的得分(X1)。

現(xiàn)應用以上方法評價學號為143030101的學生綜合素質。專家評分后的各個因素最后得分如下：

X1=8,X2=7,X3=6,X4=4,X5=1,X6=7,X7=5,X8=3,X9=6,X10=6,X11=4,X12=6,X13=7 把各個因素的得分代入我們的評價模型得出該學生的綜合素質評為:5.025；參照四川托普信息技術職業(yè)學院學生綜合素質評定標準(優(yōu)秀：Xi》9；良好：8《Xi< 9；中等：7《Xi<8；合格：6《Xi<7；不合格：< 6)，得出該學生的綜合素質成績較低，評定結果為不合格。

3 結論

本文應用層次分析法，建立了高職學生綜合素質評價的數(shù)學模型，從而使對大學生綜合素質的評價有了定量分析的評價體系。層次分析法使得該數(shù)學模型減少了人為的主觀因素，使評價更加科學、公正、客觀。該模型在學生的評比、選優(yōu)過程中具有較大的應用價值，現(xiàn)實意義較強，同時也可推廣到考評教師、干部、領導班子等的復雜系統(tǒng)中。

[1] 姜啟源等編．數(shù)學模型[M]．北京高等教育出版社，1987年第 1版。

[2] 侯定丕．層次分析法(AHP)案例報告[J]．運籌與管理，1992，1．

[3]T．L．Satty：TheAnalyticIerachyProcess，1980．

謝紅軍(1982-)，四川廣安人，四川托普信息技術職業(yè)學院招生辦，研究方向：數(shù)學教育。劉子賢(1979-)，四川樂山人，四川省犍為一中，研究方向：數(shù)學教育。

O225

A

1672-5832(2016)09-0071-01