“歸納、類比與猜想”在小學數學中的教學應用

廖平安

(深圳市龍華新區清湖小學 廣東 深圳 518000)

“歸納、類比與猜想”在小學數學中的教學應用

廖平安

(深圳市龍華新區清湖小學 廣東 深圳 518000)

在小學數學教材中有許多法則、公式等，是按照從特殊到一般的認識規律，通過對特例的觀察、分析、實驗，從而歸納出一般性結論，即歸納法。類比在數學知識延伸拓展過程中常借助于比較、聯想來啟發誘導以尋求思維的變異和發散。在歸納知識系統時又可用來串聯不同層次的類似內容，幫助理解和記憶。在解決問題時，無論是對于命題本身或解題方法，都是產生猜測、獲得命題的推廣或引伸的原動力。因此，歸納法和類比法既是數學學習的重要方法，也是數學發現的有效方法。歸納和類比都屬于合情推理，其結論需要演繹證明。猜想是歸納與類比的成果，它們都包含有猜想的成分，所以猜想本身就是一種合情推理，直截了當一點，合情推理就是猜想。牛頓說過：“沒有大膽的猜想，就做不出偉大的發現。”因此，合理地設計富有猜想的教學過程，不僅可以很好地組織教學，而且還可以提高學生學習興趣，培養學生的創新能力。

1 歸納法

歸納法是通過對同一類事物的特殊對象的研究而得出一般性結論的方法，也就是由特殊到一般的推理方法。歸納法作為數學發現的一種重要方法，在小學數學的探究學習和再創造學習中應用非常廣泛。尤其是在一些公式、法則、性質、規律等知識的推導往往是通過列舉幾個特殊的例子的基礎上歸納出來的。因此教師在教學時，要給予足夠的時間讓學生進行觀察、實驗、操作，鼓勵學生進行分析、比較，找出事物的共性和差異，并組織他們清楚地表達自己的思考過程與結果，學會簡單解釋歸納推理的過程與依據。

在小學數學歸納的教學，主要體現在以下幾個方面。

1.1 法則的歸納

對于整數的加、減、乘、除的計算，都是通過幾個具體的由易到難的例子，讓學生在理解算理和口算方法的基礎上探索計算的方法，最后進行交流和算法的總結，四則運算法則的得出就是運用了歸納法。

1.2 性質的歸納

商不變的規律，小數的性質、分數的性質、比的性質、比例的性質、等式的性質等等，是小學數學中重要的性質，這些性質的獲得，也都是通過幾個例子，讓學生進行觀察、探索、交流，最后歸納總結而得到的。

1.3 公式的歸納

小學數學的數量關系式有很多，其中典型的計算公式主要是圖形的周長、面積和體積公式。這些計算公式，也都是通過具體動手操作，猜想并驗證，進而歸納出來的。

1.4 定律的歸納

小學生最早學習的運算律是關于整數加法和乘法的運算定律，即加法交換律、加法結合律、乘法交換律、乘法結合律、乘法分配律。這些運算律的產生，也是通過計算幾組算式來觀察并猜想，從特殊到一般，從而歸納出來的。

1.5 規律的歸納

小學數學中的規律主要有圖形、數列、算式的規律，乘法和除法的變化規律等。這些規律的發現頁主要是通過一些具體的例子的觀察、比較、聯想，再提出猜想，這是歸納法的典型應用。比如，在乘法中，一個因數不變，另一個因數擴大到原來的幾倍，積就擴大到原來的幾倍。這也是通過運用歸納法得到的。

當然，在小學數學的教學中，學生的推理能力處于初步發展階段，很難對發現的規律進行證明，一般情況下都是通過再舉一些例子進行驗證。引導學生在操作、觀察等活動中學生進行分析、比較，找到簡單的事物的共性與差異，探索給定情境中隱含的規律和變化趨勢，驗證通過歸納推理得出的結論是否正確，并能解釋歸納推理的過程和依據。這些對學生的數學學習，對學生推理能力的發展有著實際的意義。

2 類比

類比法就是根據不同的兩個(或兩類)對象之間在某些方面的相似或相同，從而推出它們在其他方面也可能相似或相同的推理方法。它是以比較為基礎的一種從特殊到特殊的推理方法。類比法是由此及彼以及由彼及此的聯想方法，著名數學教育家波利亞指出“類比是一個偉大的引路人”，教師在教學中必須善于引導學生去聯想、類比，才能充分調動學生的想象力，讓他們通過比較去發現、去認識、去掌握知識。培養具有創造能力的人才，就要幫助他們學會歸納和類比。類比具有啟迪思維、提供線索、舉一反三的作用，對發展思維特別是創造性思維十分有利。和歸納一樣，類比在小學數學中也隨處可見。如通過類比，從加法、減法的運算性質(或定律)很容易聯想到乘法、除法的相應的運算性質(或定律)，由除法中各部分之間的關系，容易聯想到分數的基本性質等。

同時，類比法是系統掌握新知識、鞏固舊知識，使新舊知識融會貫通的有效方法。數學的發展是一個不斷地從原有知識向深度和廣度推進的過程，所以，各個系統的知識與知識之間必然存在著相似之處，更何況，許多知識的發展就是類比發現的結果。在實際教學中，教師必須有意識地引導學生注意知識之間的比較，如分數與除法的類比，乘法與加法的類比等。從舊知識去發現新知識，這不僅僅能起到事半功倍的效果，還將會大大提高學生的學習興趣，取得良好的學習效果。在小學的數學教學中，類比的應用主要體現以下幾個方面。

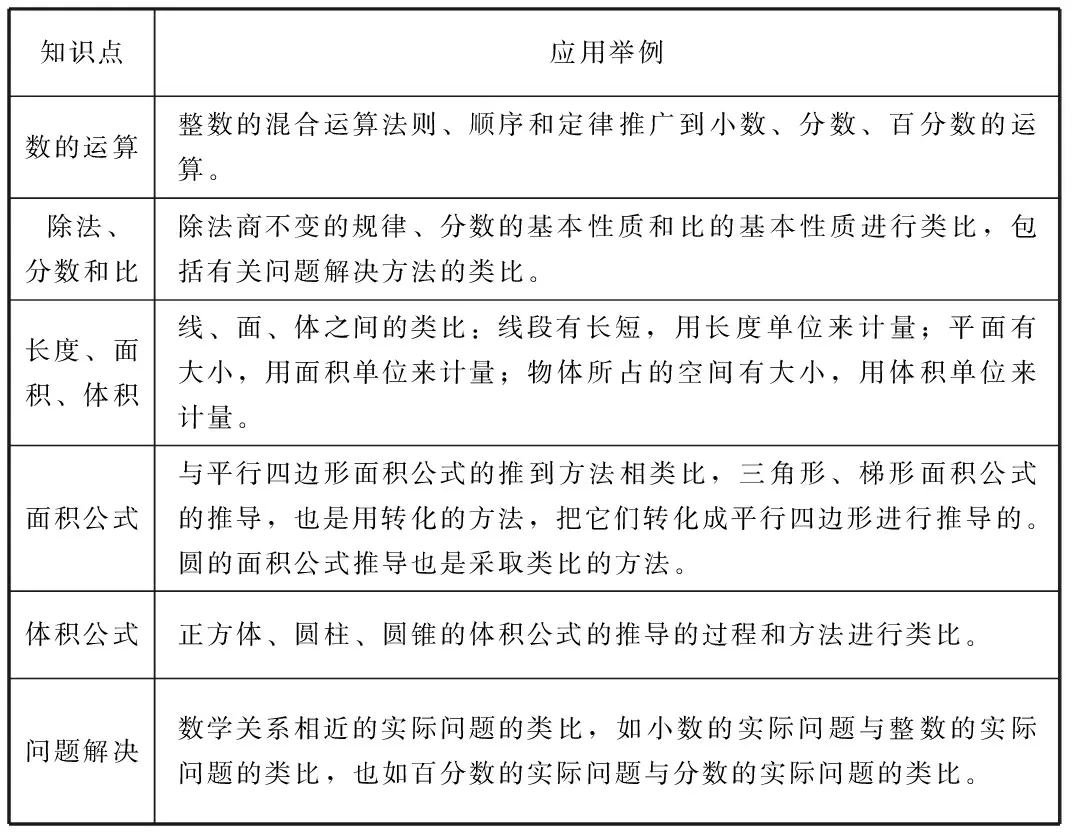
知識點應用舉例數的運算整數的混合運算法則、順序和定律推廣到小數、分數、百分數的運算。除法、分數和比除法商不變的規律、分數的基本性質和比的基本性質進行類比,包括有關問題解決方法的類比。長度、面積、體積線、面、體之間的類比:線段有長短,用長度單位來計量;平面有大小,用面積單位來計量;物體所占的空間有大小,用體積單位來計量。面積公式與平行四邊形面積公式的推到方法相類比,三角形、梯形面積公式的推導,也是用轉化的方法,把它們轉化成平行四邊形進行推導的。圓的面積公式推導也是采取類比的方法。體積公式正方體、圓柱、圓錐的體積公式的推導的過程和方法進行類比。問題解決數學關系相近的實際問題的類比,如小數的實際問題與整數的實際問題的類比,也如百分數的實際問題與分數的實際問題的類比。

類比是發現的基礎，是創新的前提。無論是學習新知識，還是利用已有的知識解決新問題，如果能夠把新知識和新問題與已有的相類似的知識進行類比，進而找到解決問題的方法，體現了知識和方法的遷移。教學時，教師就可以啟發、引導學生通過聯想、類比來探索結果，提高解決問題的能力。應用類比，關鍵在于發現兩類事物相似的性質，因此，觀察、比較、聯想是類比的基礎。教師要鼓勵學生細心觀察、動手操作、比較分析，尋找新舊知識之間的聯系，發展類比推理能力。

3 猜想

數學猜想是指根據某些數學現象而做出的預測性判斷，以及做出這些判斷的思維過程。數學家波利亞指出：“在證明一個數學定理之前，你先得猜想這個定理的內容，在你完全做出詳細證明之前，你先得推測證明的思路，你先得把觀察到的結果加以綜合，然后加以類比。你得一次又一次地進行嘗試。數學家的創造性工作成果，是論證推理，即證明；但這個證明是通過合情推理，通過猜想而發現的。”因此，在數學教學中必須重視猜想。學生在課堂上積極、主動地探究，需要猜想來引發。沒有猜想，就不會有探究。徐利治說：“探索性思維中最關鍵的環節是提出一個有希望的合理的猜測。”猜想是探索性思維的方向，具有定位性、開拓性和創造性，是數學發現與數學證明的前兆。數學解題與數學發現一樣，通常都是在通過類比、歸納等探測性方法進行探測的基礎上，獲得對有關問題的結論或解決方法的猜想，然后再設法證明或否定猜想，進而達到解決問題的目的。

當前新課程改革課堂教學的主要模式是創設情境，提出猜想(通過歸納或類比)，驗證猜想(一般由合情推理來完成)，深化理解，總結提高。比如在教學3的倍數的特征時，因為學生已經積累了探索2和5的倍數特征的經驗，因此對于3的倍數特征，教師可以放手先讓學生進行大膽猜想。很多學生會理所當然地認為“末尾是3、6、9的數是3的倍數”，教師可以肯定學生的大膽猜想，鼓勵學生舉例一些3的倍數幫助驗證，進行分析觀察，對原猜想進行驗證、修正、完善，從而得到正確的結論：3的倍數的特征是各個數位的數字之和是3的倍數。認識3的倍數特征之后，繼續探究9的倍數的特征如何？教師引導，尋找3與9的關系，通過類比來引導學生提出猜想，并繼續驗證猜想，從而得到9的倍數的特征是：各個數位上的數字之和是9的倍數。

學生思維活躍，富于幻想，敢于猜想。但是，受知識、經驗的限制，有時會提出一些幼稚可笑甚至錯誤的想法，這時教師非但不能諷刺打擊，給予抹殺，反而應該加以鼓勵，給予正確引導。讓他們保持思維的積極性，給以他們敢想的勇氣。因為這些看似可笑、錯誤的想法，總是蘊含著孩子們的創造性思維的成果。那些不拘一格的猜想，就是創造性思維的體現。

推理作為一般性的數學方法，對學生數學學習的可持續發展尤為重要。推理能力的形成和提高需要一個長期的、循序漸進的過程。數學教學活動的實質是數學推理，“合情推理”是小學生特別容易接受的一種推理方式，在小學階段，教師應重視學生的數學思考，讓學生形成推理的意識和習慣，這對于培養他們追求真理、實事求是的科學態度具有十分重要的意義。鑒于數學的嚴謹性，必須時適地引導學生對“合情推理”、“猜想”得到的結果給予嚴格說明(證明)的必要性。因為，只有經過合情推理、嚴格論證的結論，才具有真理性，誰也無法否認。而凡是偏離這兩條原則獲得的結論，不管怎樣錯綜復雜、撲朔迷離，終究會被推翻或淘汰。

教學中，教師應給予平臺讓學生充分探究，親身體驗數學知識產生過程的一般方法，體會數學的思想和方法之魅力。小學生長期在這樣的環境的熏陶下，敢于發現，敢于猜想，敢于創新，又有根據、有條理的思考問題的習慣將會慢慢地養成。

G623.5

A

1672-5832(2016)04-0157-02