基于動態執行機構的欠驅船舶循跡控制*

徐海祥　瞿　洋　余文曌　殷進軍　龍　飛

(高性能船舶技術教育部重點實驗室1)　武漢　430063)　(武漢理工大學交通學院2)　武漢　430063)

(武漢船用電力推進裝置研究所3)　武漢　430063)

?

基于動態執行機構的欠驅船舶循跡控制*

徐海祥1，2)瞿洋2)余文曌1，2)殷進軍3)龍飛3)

(高性能船舶技術教育部重點實驗室1)武漢430063)(武漢理工大學交通學院2)武漢430063)

(武漢船用電力推進裝置研究所3)武漢430063)

摘要：欠驅船舶的循跡控制已成為國內外動力定位研究的難點.針對船舶循跡控制中橫向偏差最小問題，文中利用line-of-sight (LOS) 引導律將船舶期望位置轉化為期望首向；為了滿足動態執行機構的飽和、死區和遲滯等物理限制，將執行機構的動態響應方程并入到三自由度操縱數學模型中，使控制輸出更加平滑；針對欠驅船舶橫向控制力無法滿足的問題，設計了一種基于Lyapunov理論的兩輸入反步積分控制器.數值仿真驗證了執行機構的動態響應方程和反步積分控制器的有效性.

關鍵詞：動態執行機構；循跡控制；LOS引導律；反步積分

徐海祥(1975- )：男，博士，教授，博士生導師，主要研究領域為海洋動力定位系統開發

*國家自然科學基金資助(批準號：61301279)

0引言

船舶循跡控制是指船舶在作業或航行過程中，沿某一條預定軌跡以恒定的縱向速度前進，在此過程中必須保持船舶的首向沿著預定軌跡.船舶循跡控制的控制目標主要包括航跡的保持和縱向速度的控制[1].在循跡控制過程中，船舶所需的首向角由引導系統產生.

欠驅船舶循跡控制是船舶循跡控制的一個難點.欠驅船舶是指船舶的執行機構的配置無法同時滿足縱向、橫向和首向的控制要求.對于欠驅船舶而言，其配置形式一般是主推與舵，主推用于產生船舶前進所需的速度，而舵主要產生轉首力矩.欠驅船舶的最低配置是一個主推和單舵的組合，其執行機構往往只有主推和舵機，船舶的橫向控制力是無法滿足的.早期，欠驅船舶的循跡控制問題常用到的是野本謙作(Nomoto)操縱數學模型，但其缺點是不能將環境擾動力里考慮到模型當中[2].20世紀90年代后期，三自由度的船舶操縱數學模型在欠驅船舶控制中得到了應用，其可以考慮船舶縱向和首搖方向的環境擾動力影響，但無法考慮到橫向擾動力的影響[3-4].隨后，國內外欠驅船舶循跡控制的研究重點轉為如何抵抗環境擾動力，特別是流的影響[5-7].

由于假設執行機構能夠迅速滿足控制輸出，因而執行機構的動態響應往往被忽略.但實際的執行機構存在飽和、死區和遲滯等物理限制，因此執行機構的動態響應不能夠被忽略.對于動態執行機構問題，大多數的做法是將其考慮到推力分配的靜態分配當中，但這種做法無法從根本上解決高頻控制輸出的問題[8]；較好的做法是將其考慮到操縱數學模型中，使控制器的設計不僅能夠能滿足整個系統的穩定而且控制輸出相對平滑[9].一般，執行機構的動態響應方程可視為具有低通濾波功能的一階慣性環節.

針對欠驅船舶循跡控制問題，以上文獻大都側重于如何抵抗外部環境擾動力而忽略了執行機構動態響應問題.在以上文獻的基礎上，本文利用LOS引導律將船舶期望位置轉化為期望首向，在三自由度操縱數學模型中考慮動態執行機構方程，利用Lyapunov理論設計了一種不考慮橫向控制力的反步積分控制器，實現了對未建模環境力的補償.

1引導律的設計

對于船舶循跡控制來說，引導律的設計是在一個二維平面坐標系內完成的.首先引入路徑平行坐標系(path parallel)的概念，該坐標系的X軸與路徑相切，Y軸與X軸垂直形成右手坐標系，見圖1.相較于更加復雜的一般曲線引導系統的設計，這里將介紹基于直線和圓弧的引導系統的設計.圖中Pp點為路徑平行坐標系的原點；P點為船體坐標系原點.

對于直線路徑來說，船舶此時所需要的首向ψd即為圖中所示的引導首向角χs，χs可表示為

(1)

圖1　直線和圓弧的LOS引導律

對于圓弧路徑來說，船舶此時所需要的首向ψd即為圖中所示的引導首向角χc，χc可表示為

(2)

為了減小循跡控制過程中的振蕩，時變的前向距離Δ可取為[10]

(3)

式中：ρ為前向距離Δ的收斂速率.當偏差越大時，Δ越小，以此獲得較快的轉首，反之Δ越大，以此減小較小Δ引起的振動.

2船舶數學模型

考慮到執行機構的動態響應方程，三自由度船舶操縱數學模型為

(4)

(6)

式中：η=[x,y,ψ]T為船體在固定坐標系下的位置；v=[u,υ,r]T為船體在運動坐標系下的速度；R(ψ)∈R3×3為坐標系旋轉矩陣；MRB∈R3×3為剛體慣性矩陣；MA∈R3×3為附黏水慣性矩陣；D∈R3×3是阻力的線性部分；Bu為船舶執行機構的配置矩陣；up=[Tp,δ]T為螺旋槳推力Tp和操舵角δ組成的向量；τw為風載荷，主要依據風載荷系數，風向βw和風速Vw計算；b∈R3×1是作用于船體上的未建模環境擾動力，包括風浪流的未建模擾動力；Tu為表征執行機構動態響應速率的定常矩陣；uc=[Tpc,δc]T為控制器的輸出；vr是船體在運動坐標系下相對于流速vc的相對速度.vr和v的關系可以表示成如下形式.

(7)

式中：Vc和βc分別為流速的大小和流向角.考慮到執行機構的飽和問題，控制器的輸出需要作如下限制.

(8)

3反步積分控制器設計

在文獻[11]的研究基礎上，本文根據線性操縱運動模型進行自適應未建模環境力的反步積分控制器設計.

定義有如下的投影向量和偏差向量.

(9)

式中：α1=[α11,α12,α13]T∈R3為虛擬控制項.

第一步，第一個Lyapunov函數定義為

(10)

對上式求導：

(11)

將式代入上式得

(12)

因此，虛擬控制量α13可以選為

(13)

式中，c1>0，式(12)可以化簡為

(14)

第二步，定義第二個Lyapunov函數：

(15)

對式(15)求導：

根據線性操縱運動數學模型

(17)

式中：Buup可作為第二個虛擬控制量.因此，式(16)可以寫為

(18)

因此，虛擬控制量α2可取為：

rMASTR(ψ)Tvc-DR(ψ)Tvc-K2z2

(19)

式中：K2為正定的對角矩陣，取如下的自適應的未建模環境力：

(20)

定義第三個偏差向量：

(21)

第三步，第三個Lyapunov函數定義為：

(22)

對式(22)求導，并帶入式(6)、(18)和(19)得：

(23)

對于欠驅動船舶，其三個方向的控制力為τ=Buup.為了滿足轉首力矩τ3，橫向控制力就無法滿足，通常可以假定橫向控制力為零，即τ2=0.對于實際的船舶，其轉首力矩通常由操舵產生，同時也會產生相應的橫向力，即τ2=ετ3，參數ε=Yδ/Nδ不為零，控制力的形式可以表示為

(24)

針對欠驅船舶推力和操舵角存在動態限制的問題，可將配置矩陣Bu進行降維處理.

(25)

結合式和式，為了使系統穩定，縱向和首向的控制率可以設計為

(26)

(27)

在循跡控制過程中，希望船舶沿某一條預定軌跡以恒定的縱向速度ud前進，在此過程中必須保持船舶的首向沿著預定軌跡.因此，虛擬控制項α1可以寫成如下形式.

(28)

4實驗仿真

本文仿真中用到的船模是挪威科技大學的Cybership 2，模型、LOS引導律、控制器和環境力等參數的設定值見表1.設定的4個軌跡點坐標及相應的圓弧半徑為：P1=(0,0),P2=(5,20),P3=(20,15),P4=(30,30),Ri=(3,3).

針對循跡控制對位置保持和速度控制的要求，結合所設計的自適應未建模環境力反步積分控制器，文中給出了相關的仿真結果圖.圖2顯示了循跡控制中的反步積分控制器具有非常好的效果，船舶的橫向偏差在很短時間內迅速減小.圖3說明在仿真開始后的前面若干個周期內，時變的前向距離Δ能使船舶迅速轉首到所需的首向角，隨后的控制首向也與所需的船舶首向吻合得非常好.圖4給出了船舶循跡過程中的橫向偏差，仿真結果說明船舶穩定狀態下的橫向偏差均在0.1 m以下.圖5顯示了船舶的縱向速度控制得非常好，保持在0.1 m/s左右，橫向速度在最后也慢慢趨近于零.這從側面也證明了即使橫向控制無法滿足，只要時間足夠長，橫向速度會慢慢趨近于零.圖6說明了自適應未建模環境力慢慢地趨近于設定的未建模環境力，反應了未建模環境力自適應律的有效性.圖7顯示了欠驅船舶在只滿足縱向推力和轉首力矩條件下的控制輸出uc，由于設計控制器時將控制量設為螺旋槳推力和操舵角，因此可以更為直接地將螺旋槳推力和操舵角的輸出限制考慮進來，盡量避免出現無法分配所需控制力的情況.另外，在控制器設計過程中還考慮了執行機構的動態響應過程，將控制量設為uc而非實際輸出up，這樣便能夠讓控制信號更好地滿足船舶的實際響應需求.

表1　相關參數設定值

圖2　船舶運動軌跡圖

圖3　船舶實際首向角和所需首向角

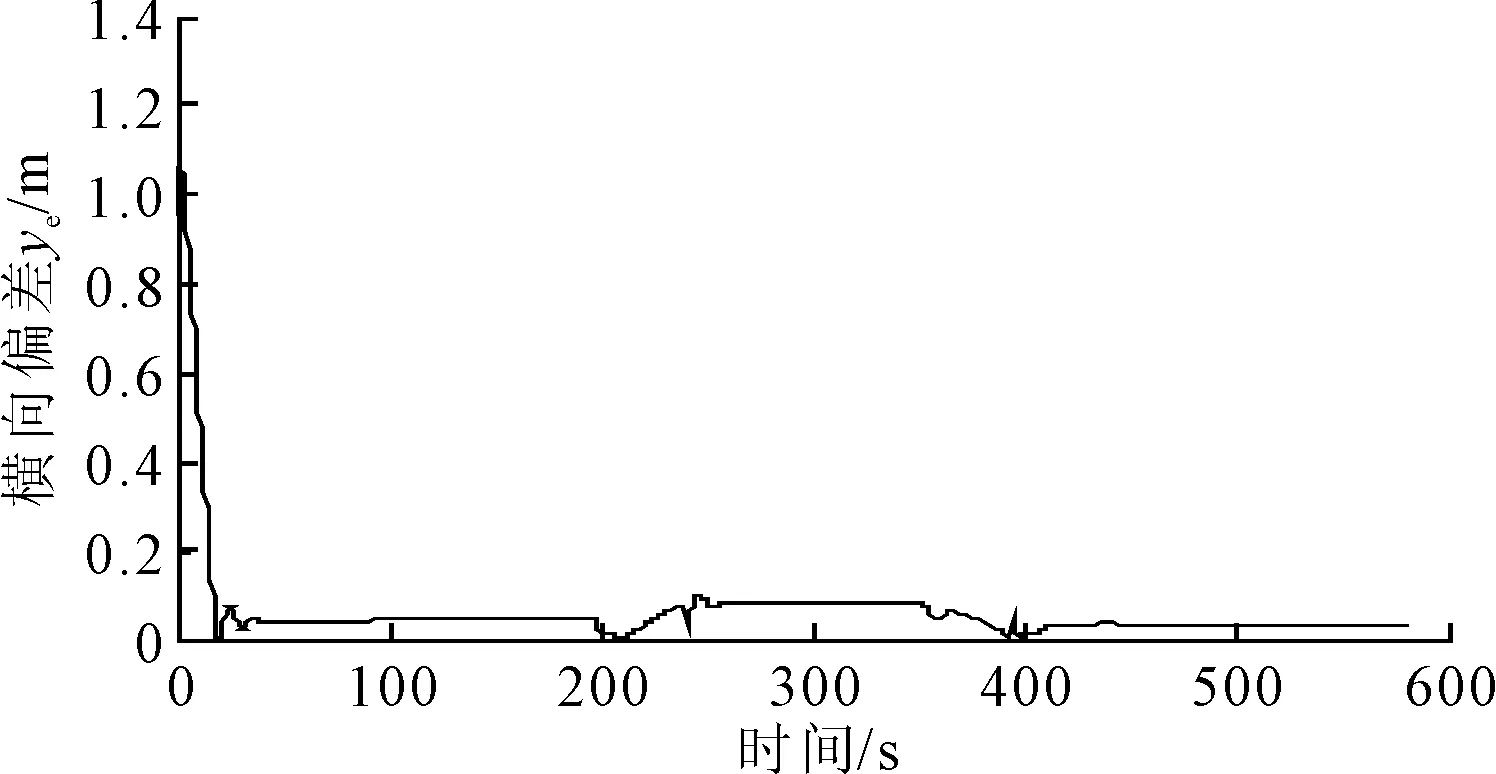
圖4　船舶橫向偏差

圖5　船舶運動的速度

圖6　自適應未建模環境力

圖7　船舶控制輸出uc

5結 束 語

針對欠驅動船舶循跡控制中的航跡保持問題，本文利用了LOS引導律來獲得船舶所需的首向角，同時使循跡控制過程中的橫向偏差最小.針對動態執行機構存在物理限制和欠驅船舶橫向控制力無法滿足的問題，本文將執行機構動態響應方程并入到三自由度操縱模型中，設計了不考慮橫向控制力的兩輸入反步積分控制器，實現了對未建模環境力的在線自適應補償，達到了對船舶首向和前進速度平穩控制的目的.

參 考 文 獻

[1]SKJETNE R, FOSSEN T I， KOKOTOVIC P. Output maneuvering for a class of nonlinear systems[C]. Proceedings of the 15th IFAC World Congress on Automatic Control, Barcelona, Spain,2002.

[2]FOSSEN T I. Guidance and gontrol of ocean vehicles[M]. Hoboken： John Wiley & Sons,1994.

[3]SIRA R H. On the control of the underactuated ship: A trajectory planning approach[C]. Proceedings of the 38th IEEE Conference on Decision and Control,1999(3):2192-2197.

[4]PETTERSEN K Y, FOSSEN T I. Underactuated dynamic positioning of a ship-experimental results[J]. IEEE Transactions on Control Systems Technology,2000,8(5):856-863.

[5]MENG W, GUO C, CHEN R. Adaptive output feedback control for path following of underactuated ships with uncertain dynamics[C]. Proceedings of the 27th Conference on Control and Decision,2015:5383-5386.

[6]CAHARIJA W. Integral line-of-sight guidance and control of underactuated marine vehicles[D]. Norwegian： Norwegian University of Science and Technology,2014.

[7]LEKKAS A M. Guidance and path-planing system for autonomous vehicles[D]. Norwegian：Norwegian University of Science and Technology,2014.

[8]BERGE S P, FOSSEN T I. Robust control allocation of overactuated ships; experiments with a model ship[C]. Proceedings of the 4th IFAC Conference on Manoeuvring and Control of Marine Craft，1997:166-171.

[9]MORISHITA H M， SOUZA C E S. Modified observer backstepping controller for a dynamic positioning system[J]. Control Engineering Practice,2014,33:105-114.

[10]LEKKAS A M, FOSSEN T I. A time-varying lookahead distance guidance law for path following[C]. Proceedings of 9th IFAC Conference on Manoeuvring and Control of Marine Craft, Arenzano, Italy,2012.

[11]FOSSEN T I, BREIVIK M， SKJETNE R. Line-of-sight path following of underactuated marine craft[C]. Proceedings of the 6th IFAC MCMC, Girona, Spain,2003:244-249.

Path Following for Underactuated Marine

Craft with Actuator Dynamics

XU Haixiang1，2)QU Yang2)YU Wenzhao1，2)YIN Jinjun3)LONG Fei3)

(KeyLaboratoryofHighPerformanceShipTechnology

ofMinistryofEducation,Wuhan430063，China)1)

(SchoolofTransportation,WuhanUniversityofTechnology,Wuhan430063，China)2)

(WuhanInstituteofMarineElectricPropulsion,Wuhan430063，China)3)

Abstract：Recently, path following for underactuated marine craft has become a difficult problem. To minimize the cross-track error to the path, a line-of-sight (LOS) guidance law is introduced to reduce the control outputs from the desired position to the desired heading angle. In order to satisfy the saturations, dead-zones and hysteresis of the actuators, the actuator dynamics equation is added into the 3DOF maneuvering model to obtain a smooth control outputs. Considering that the sway force of the underactuated ship could not be satisfied, a backstepping controller with two outputs has been designed based on Lyapunov theory. In addition, the validity of the actuator dynamics equation and the backstepping controller is demonstrated by the simulation using the maneuvering model.

Key words：actuator dynamics; path following; line-of-sight guidance; backstepping

收稿日期：2015-10-09

doi:10.3963/j.issn.2095-3844.2016.01.002

中圖法分類號：U675.91