螺旋槳流固耦合方法及噪聲預(yù)報*

楊　光　熊　鷹　黃　政

(海軍工程大學(xué)艦船工程系　武漢　430033)

?

螺旋槳流固耦合方法及噪聲預(yù)報*

楊光熊鷹黃政

(海軍工程大學(xué)艦船工程系武漢430033)

摘要：采用ANSYS Mechanical有限元計算模塊結(jié)合基于粘性流理論的計算流體力學(xué)方法在Workbench平臺上對材料為鎳鋁青銅的DTMB4381槳進(jìn)行雙向流固耦合計算，提出順序求解和同步求解2種方法，并與傳統(tǒng)的計算流體力學(xué)方法對比分析，驗證雙向流固耦合方法的可行性和優(yōu)越性.在僅考慮旋轉(zhuǎn)偶極子聲源的情況下，基于分離渦模型(DES)求解槳葉表面時域內(nèi)脈動壓力，然后采用邊界元方法對某標(biāo)稱伴流場中的5葉大側(cè)斜螺旋槳進(jìn)行氣動聲學(xué)計算，預(yù)報剛性槳無空泡噪聲特性.在相同工況下，以雙向流固耦合方法為手段，通過傅里葉變換探究材料特性對螺旋槳噪聲的影響.

關(guān)鍵詞：螺旋槳；雙向流固耦合；旋轉(zhuǎn)偶極子；無空泡噪聲

楊光( 1990- )：男，碩士生，主要研究領(lǐng)域為艦船流體動力性能

*國家自然科學(xué)基金項目資助(批準(zhǔn)號：51179198)

0引言

復(fù)合材料由于其自身的優(yōu)越性[1]，被廣泛地應(yīng)用到造船領(lǐng)域中，復(fù)合材料螺旋槳就是最主要的應(yīng)用之一.由于復(fù)合材料螺旋槳獨(dú)特的彎扭耦合特性，傳統(tǒng)的理論預(yù)報(升力面、面元法)和計算流體力學(xué)方法已經(jīng)不足以對其進(jìn)行數(shù)值預(yù)報和深入的理論研究.國內(nèi)外專家學(xué)者對復(fù)合材料螺旋槳進(jìn)行了大量流固耦合研究[2-8],但以往的流固耦合方法大多采用基于勢流理論的面元法，沒有考慮流體的粘性；或者是通過手動迭代的穩(wěn)態(tài)求解，均具有一定的局限性.

流固耦合方法是20世紀(jì)80年代興起的一門多物理場交叉學(xué)科，涉及流體和結(jié)構(gòu)的相互作用.流固耦合按數(shù)據(jù)的傳遞方向可分為單向和雙向2種方式；按照控制方程可分為“強(qiáng)”“弱”2種耦合方式，“強(qiáng)”耦合是將流、固控制方程耦合到一個方程矩陣中求解，但這種求解方法對計算機(jī)要求十分高，在實際應(yīng)用中很難實現(xiàn)，因此普遍采用“弱”耦合方法，即分別求解流體控制方法和固體控制方程.在Workbench中耦合可分為順序和同步兩種求解方法，順序求解需要設(shè)定流體計算和固體計算的優(yōu)先級，按順序求解；而同步求解是同時進(jìn)行流體計算和固體計算.文中分別采用流固耦合2種方法和傳統(tǒng)的CFD計算方法對材料為鎳鋁青銅的DTMB4381槳進(jìn)行性能預(yù)報,對結(jié)果進(jìn)行對比分析驗證流固耦合方法的可行性.

最后，文中基于FW-H方程采用聲學(xué)邊界元方法對某標(biāo)稱伴流場中剛性槳進(jìn)行無空泡噪聲預(yù)報.然后改變螺旋槳材料，通過雙向流固耦合方法和傅里葉變換研究材料對噪聲性能的影響.

1流固耦合計算

采用計算流體力學(xué)軟件CFX和有限元軟件ANSYS Mechanical在Workbench平臺上通過MFX求解器進(jìn)行雙向流固耦合數(shù)值計算.在耦合求解步中，通過流固耦合面?zhèn)鬟f流體計算結(jié)果和固體計算結(jié)果，流體載荷使槳葉產(chǎn)生變形，變形后的槳葉又影響周圍流場，實現(xiàn)流體載荷改變固體形狀和固體變形改變周圍流場的實時傳遞，直到滿足殘差要求計算停止.選擇DTMB4381槳為研究對象，DTMB4381為5葉槳，槳模直徑為0.305 m，無縱傾無側(cè)斜.由于流固耦合計算時間較長因此只對進(jìn)速系數(shù)J=0.9工況進(jìn)行計算.

1.1計算模型

1.1.1流體計算模型

根據(jù)DTMB4381槳型值參數(shù)通過MATLAB編程得到各半徑處槳葉剖面三維坐標(biāo)點(diǎn)，在ICEM CFD中對螺旋槳及計算流域進(jìn)行建模及網(wǎng)格劃分，計算流域分為旋轉(zhuǎn)域和靜止域，為了確保槳葉網(wǎng)格具有周期性，文中采用結(jié)構(gòu)化網(wǎng)格，首先對1/5旋轉(zhuǎn)域創(chuàng)建拓?fù)浣Y(jié)構(gòu)，通過坍塌、點(diǎn)線面映射等命令劃分網(wǎng)格，采用O-block解決槳葉周圍block頂點(diǎn)處網(wǎng)格扭曲的情況，提高網(wǎng)格質(zhì)量，為了更好地捕捉槳葉周邊流場的流動情況，在槳輪廓線周圍以及葉根處加密，葉根處第一層網(wǎng)格尺寸為槳葉直徑的1/1 000，見圖1.通過周期性旋轉(zhuǎn)得到內(nèi)域整體網(wǎng)格并與靜止域合并，得到最終的流體計算模型，見圖2.網(wǎng)格質(zhì)量最終為0.37，網(wǎng)格數(shù)為2 923 076.

圖1　1/5旋轉(zhuǎn)域網(wǎng)格

圖2　流體計算域網(wǎng)格

1.1.2有限元模型.

通過已有的槳葉三維坐標(biāo)點(diǎn)在建模軟件Solidworks中建立DTMB4381槳實體模型，將其導(dǎo)入結(jié)構(gòu)計算模塊中，在結(jié)構(gòu)計算模塊中進(jìn)行實體有限元網(wǎng)格劃分，網(wǎng)格數(shù)為34 792，見圖3.在ANSYS mechanical中設(shè)定螺旋槳材料，材料參數(shù)見表1.將槳葉吸力面和壓力面分別設(shè)為流固耦合耦合面實現(xiàn)流體結(jié)果和固體計算結(jié)果的實時交替，并將槳轂設(shè)置為固定約束，見圖4.

圖3　螺旋槳有限元模型

圖4　有限元計算邊界條件

材料ρ/(kg·m-3)E/GPaμN(yùn)AB74001240.33

1.2流固耦合設(shè)置

流固耦合采用順序求解方法時，流體計算和結(jié)構(gòu)計算時間步長均為0.04 s，進(jìn)速系數(shù)J=0.9，螺旋槳轉(zhuǎn)速為600 r/min，繞x軸旋轉(zhuǎn).在流體域中設(shè)置網(wǎng)格變形模擬槳葉變形，速度入口為inlet，出口為outlet，相對壓力設(shè)為0，遠(yuǎn)場、槳轂、槳葉均設(shè)為無滑移壁面，旋轉(zhuǎn)域和靜止域的交界面通過GGI連接，采用MRF技術(shù)，計算采用高階求解模式，流體計算收斂殘差為10-6，耦合收斂殘差為0.01，由于是流體引起固體變形，因此優(yōu)先進(jìn)行流體計算.本次計算分別選取三種常見的湍流模型，k-ω,SST,k-ε進(jìn)行計算，在流固耦合順序求解中k-ε,SST極易發(fā)散，因此選擇k-ε湍流模型.采用同步求解方法時，時間步長設(shè)為0.01 s，湍流模型選擇SST，流體計算收斂殘差設(shè)為10-4，交界面采用滑移網(wǎng)格技術(shù)，求解模式選擇Second Order Backward Euler，其余設(shè)置與順序求解方法相同.采用傳統(tǒng)的CFD方法將螺旋槳視為剛性，不考慮變形，采用瞬態(tài)求解，設(shè)置與流固耦合同步求解方法中的流體計算設(shè)置相同.

1.3計算結(jié)果

表2　DTMB4381水動力性能

通過對比，3種算法水動力性能kt，10kq，ηo的最大誤差分別為4.17%，1.76%，2.8%，誤差滿足工程應(yīng)用的要求.3種計算方法的水動力性能比較相近，驗證了工程中將金屬槳視為剛性槳假設(shè)的合理性，出現(xiàn)此結(jié)果的原因是鎳鋁青銅合金等金屬材料彈性模量較大，螺旋槳在水中運(yùn)轉(zhuǎn)時變形較小，螺旋槳幾何的改變對周圍流場的影響較小，而且DTMB4381槳無縱傾無側(cè)斜，結(jié)構(gòu)變形對水動力性能的影響不大.由于流固耦合順序求解法比同步求解更快的達(dá)到收斂，因此在對均勻流場進(jìn)行流固耦合計算時通常選擇順序求解；而在非均勻流場中通常選擇同步求解，可以查看任意時刻非均勻流場對螺旋槳水動力性能的影響.

采用流固耦合算法可以直接在CFD后處理中查看結(jié)構(gòu)計算結(jié)果，圖5，圖6分別為螺旋槳變形云圖和von Mises應(yīng)力分布云圖.槳葉變形由葉根至葉梢沿徑向逐漸增加，葉梢處的最大變形為3.245 4×10-5m，為螺旋槳直徑的0.01%，同樣說明了可以忽略金屬槳的變形.槳葉應(yīng)力由葉根至葉梢沿徑向逐漸降低.

圖5　螺旋槳變形云圖

圖6　von Mises應(yīng)力分布云圖

2螺旋槳噪聲預(yù)報

文中基于FW-H方程，采用噪聲計算軟件Virtual.Lab Acoustics中的直接邊界元方法對某標(biāo)稱伴流場中材料為銅合金的5葉大側(cè)斜螺旋槳進(jìn)行無空泡噪聲數(shù)值預(yù)報，不考慮槳的變形.螺旋槳噪聲源包括單極子、偶極子和四極子，四極子聲源僅在接近音速的流動中作用才比較明顯，而水流的馬赫數(shù)較低，因此四極子可以忽略不計.單極子聲源是由空泡體積的變化或者螺旋槳旋轉(zhuǎn)排開一定體積的水引起，文中不考慮空泡噪聲，文獻(xiàn)[9-10]驗證了厚度噪聲相比于負(fù)載噪聲可以忽略不計.因此文中僅考慮偶極子聲源，即槳葉表面壓力脈動所產(chǎn)生的噪聲.

5葉大側(cè)斜螺旋槳模型幾何參數(shù)見表3，首先通過CFD計算得到槳葉時域內(nèi)脈動壓力信息，流體計算模型采用ICEM CFD創(chuàng)建，選擇結(jié)構(gòu)網(wǎng)格，劃分方法與第一節(jié)相同，螺旋槳周圍第一層網(wǎng)格尺寸為0.000 18，見圖7，將旋轉(zhuǎn)域和靜止域合并得到最終計算域網(wǎng)格，見圖8，網(wǎng)格數(shù)為3 921 977，網(wǎng)格質(zhì)量為0.35以上.

圖7　槳葉、槳轂表面網(wǎng)格

圖8　流體計算域網(wǎng)格

直徑/m0.7R螺距比葉數(shù)盤面比轂徑比0.241.35650.720.2807

首先采用定常求解螺旋槳水動力性能，轉(zhuǎn)速為762 r/min，湍流模型選擇k-ω，標(biāo)稱伴流加到速度入口，見圖9，由圖9可見，伴流場沿著z軸方向變化較為復(fù)雜.計算收斂后將定常結(jié)果作為瞬態(tài)計算的初值，湍流模型選擇分離渦(DES)方法，時間步長Δt=0.000 5 s，即螺旋槳旋轉(zhuǎn)約2.3°記錄一次槳葉壓力脈動信息.計算穩(wěn)定后得到單槳葉和5個槳葉上在2個旋轉(zhuǎn)周期內(nèi)時域軸向脈動壓力曲線，見圖10、圖11.

圖9　非均勻伴流場云圖

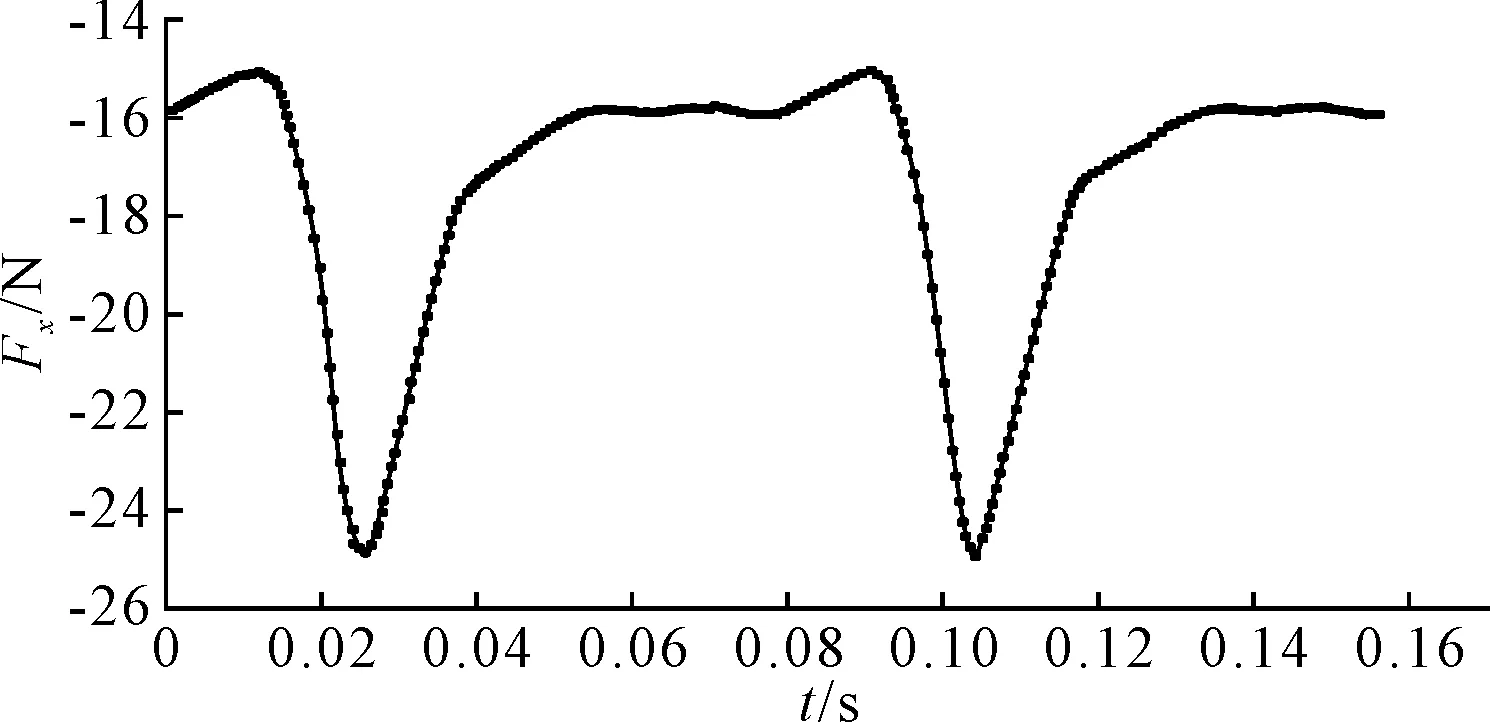
圖10　單槳葉軸向脈動壓力

圖11　槳葉軸向脈動壓力

圖12　聲學(xué)網(wǎng)格

圖13　聲場

通過計算，得到各監(jiān)測點(diǎn)的噪聲頻譜特性，圖14為x軸方向噪聲頻譜曲線.各監(jiān)測點(diǎn)的總聲壓級根據(jù)式(1)計算，見表4.

(1)

圖14　x軸監(jiān)測點(diǎn)頻譜曲線

監(jiān)測點(diǎn)x1x2y1y2z1z2SPL/dB156.47145.59123.76100.01100.1101.29

從各監(jiān)測點(diǎn)的總聲壓級可知，軸向噪聲對總噪聲貢獻(xiàn)量最大.分別對5個槳葉時域內(nèi)軸向脈動壓力進(jìn)行傅里葉變換轉(zhuǎn)換為頻域內(nèi)脈動信息，得到圖15，由圖可知，軸向脈動壓力在葉頻和倍葉頻附近出現(xiàn)幅值，與螺旋槳軸向監(jiān)測點(diǎn)噪聲頻譜曲線規(guī)律一致，而且一階葉頻處脈動壓力對總噪聲級的影響最大.接下來改變螺旋槳材料，采用雙向流固耦合方法對彈性槳進(jìn)行數(shù)值計算，研究材料特性對螺旋槳噪聲的影響.

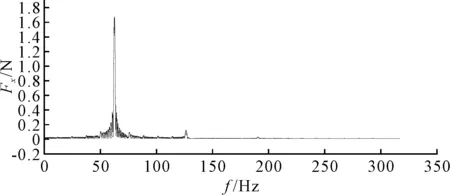
圖15　螺旋槳頻域內(nèi)軸向脈動壓力

螺旋槳材料改為各向異性的碳纖維復(fù)合材料，材料特性見表5，不考慮復(fù)合材料的鋪層結(jié)構(gòu)，工況保持不變，水動力計算模型采用剛性槳模型，有限元計算模型見圖16，首先采用順序求解法進(jìn)行雙向流固耦合計算，湍流模型選擇k-ω，待計算收斂，將其作為初值進(jìn)行瞬態(tài)雙向流固耦合計算，湍流模型選擇SST，考慮計算時間的問題，時間步長Δt=0.001 s，計算穩(wěn)定后，得到螺旋槳變形分布，見圖17，由葉根至葉梢沿著徑向變形逐漸增大，槳葉最大變形為螺旋槳直徑的0.164%，是第一節(jié)中鎳鋁青銅螺旋槳的10倍，因此對復(fù)合材料螺旋槳進(jìn)行水動力性能計算時，要考慮螺旋槳的彎扭耦合特性.

表5　材料參數(shù)

圖16　有限元模型

圖17　螺旋槳變形云圖

復(fù)合材料螺旋槳槳葉表面軸向脈動壓力見圖18.通過傅里葉變換得到復(fù)合材料螺旋槳頻域內(nèi)軸向脈動壓力，見圖19，由圖可知在葉頻附近脈動出現(xiàn)幅值，而且在葉頻和倍葉頻附近脈動幅值較金屬槳降低很多，側(cè)面反映出復(fù)合材料噪聲性能要優(yōu)于剛性槳，具有減振降噪的優(yōu)點(diǎn).圖20分別為金屬槳和復(fù)合材料螺旋槳盤面處軸向速度分布云圖，從圖中可知在伴流場變化較為復(fù)雜區(qū)域(z軸方向)，復(fù)合材料螺旋槳葉梢流場的變化較金屬槳更為平緩，這是由于復(fù)合材料螺旋槳的變形對來流具有自適應(yīng)性的原因.

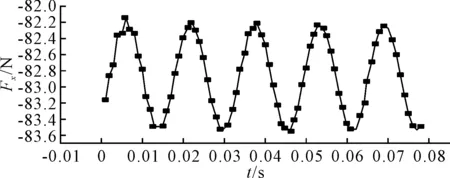
圖18　復(fù)合材料螺旋槳軸向脈動壓力

圖19　復(fù)合材料螺旋槳頻域內(nèi)軸向脈動壓力

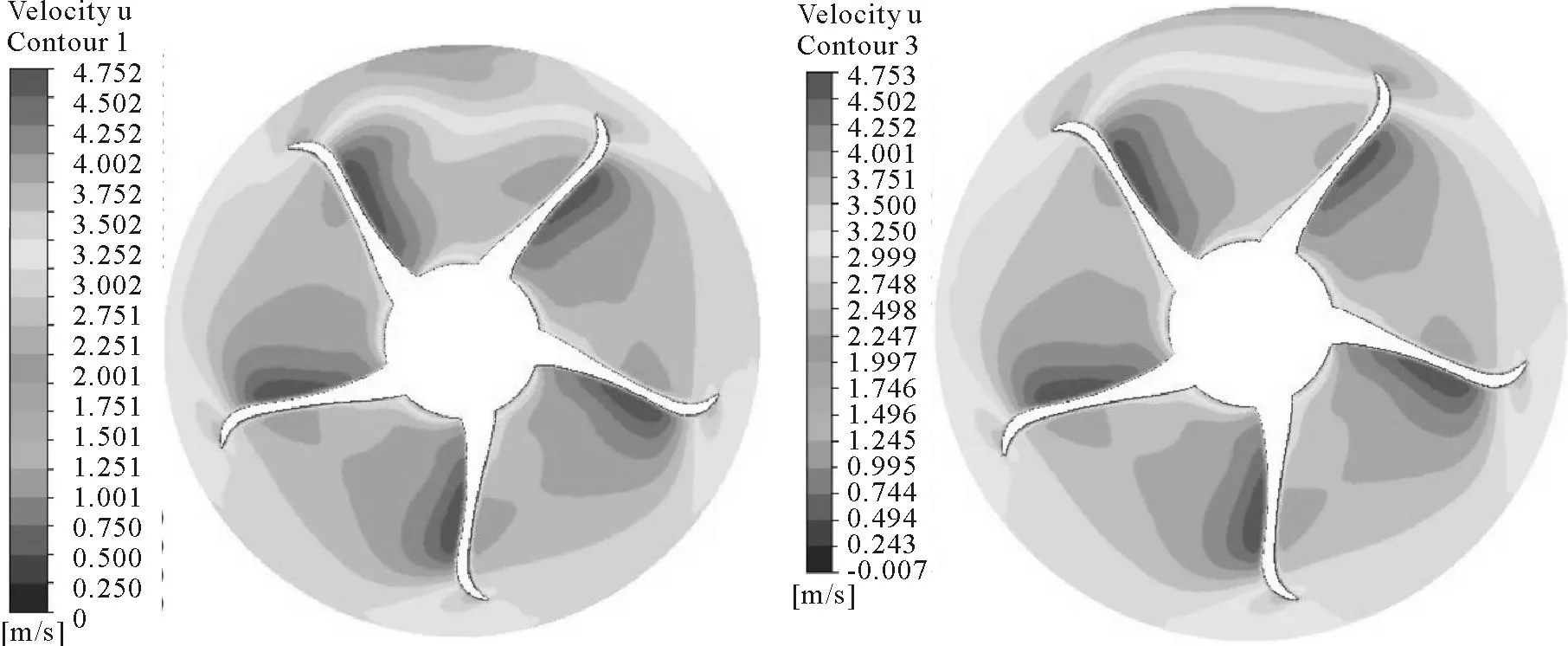
圖20　螺旋槳盤面處軸向速度分布

3結(jié) 束 語

文中采用順序和同步兩種雙向流固耦合計算方法對材料為鎳鋁青銅的DTMB4381槳進(jìn)行性能預(yù)報，在Workbench平臺上實現(xiàn)計算流體力學(xué)結(jié)果和有限元計算結(jié)果的實時傳遞.與試驗值對比，驗證流固耦合方法的準(zhǔn)確性.然后采用聲學(xué)直接邊界元方法預(yù)報了某標(biāo)稱伴流場中鎳鋁青銅合金五葉大側(cè)斜螺旋槳無空泡負(fù)載噪聲特性，說明了軸向脈動壓力和負(fù)載噪聲的關(guān)系.并在相同工況下，將此槳材料改為碳纖維復(fù)合材料，對其進(jìn)行瞬態(tài)雙向流固耦合計算，得到復(fù)合材料螺旋槳的水動力性能和結(jié)構(gòu)特性.通過對比兩個槳頻域內(nèi)脈動壓力特性，側(cè)面說明碳纖維復(fù)合材料螺旋槳具有減振降噪的優(yōu)點(diǎn).

參 考 文 獻(xiàn)

[1]張帥，朱錫，孫海濤，等.船用復(fù)合材料螺旋槳研究進(jìn)展[J].力學(xué)進(jìn)展，2012,42(5):620-633.

[2]YOUNG Y L. Time-dependent hydroelastic analysis of cavitating propulsors[J]. Journal of Fluids & Structures, 2007,23(2):269-295.

[3]YOUNG Y L. Fluid-structure interaction analysis of flexible composite marine propellers[J]. Journal of Fluids & Structures, 2008,24(6):799-818.

[4]YOUNG Y L. Fluid-structure interaction analysis of flexible composite marine propellers[J]. Journal of Fluids & Structures, 2008,24(6):799-818.

[5]LIU Z, YIN L Y. Utilization of bend-twist coupling for performance enhancement of composite marine propellers[J]. Journal of Fluids & Structures, 2009,25(6):1102-1116.

[6]LIN C C, LEE Y J. Stacking sequence optimization of laminated composite structures using genetic algorithm with local improvement[J]. Composite Structures, 2004,63(3-4):339-345.

[7]孫海濤,熊鷹.考慮變形的螺旋槳水動力及變形特性研究[J].哈爾濱工程大學(xué)學(xué)報,2013,34(9):1108-1112.

[8]張帥,朱錫,侯海量.船舶螺旋槳流固耦合穩(wěn)態(tài)求解算法[J].哈爾濱工程大學(xué)學(xué)報,2012,33(5):615-621..

[9]SEOL Hanshin,SUH Jung-Chun,LEE Soogab.Development of hybrid method for the prediction of underwater propeller noise[J]. Journal of Sound and Svibration, 2005,288(1-2):345-360.

[10]蘇玉民,竇鳳祥,劉業(yè)寶,等.螺旋槳無空泡噪聲的研究[J].武漢理工大學(xué)學(xué)報：交通科學(xué)與工程版,2013,37(5):895-899.

Fluid-structure Coupling and Numerical

Noise Prediction of Propeller

YANG GuangXIONG YingHUANG Zheng

(DepartmentofNavalEngineering,NavalUniversityofEngineering,Wuhan430033,China)

Abstract：In the commercial software ANSYS Workbench, the paper combines FEM solver ANSYS Mechanical with CFD solver based on viscous fluid theory to accomplish synchronously or sequentially two-way fluid-structure coupling of NAB DTMB4381, then compares the results from FSI method and from traditional CFD method with experimental result to confirm the validity and advancement of coupled FSI. In some non-uniform flow field ,the fluctuating pressure on blades in time domain was simulated by choosing DES as turbulence model, then non-cavitation noise of highly skewed propeller was predicted by the method of BEM only considering acoustic rotating dipole .In the same working condition, two-way FSI and FFT is used to explore the influence of blade material on propeller noise.

Key words：propeller; two-way fluid-structure coupling; acoustic rotating dipole; non-cavitation noise

收稿日期：2015-11-05

doi:10.3963/j.issn.2095-3844.2016.01.030

中圖法分類號：U664.33