也談“數(shù)形結(jié)合百般好，割裂分家萬(wàn)事休”

蔡慶全

我國(guó)著名數(shù)學(xué)家華羅庚曾說(shuō)：“數(shù)形結(jié)合百般好，割裂分家萬(wàn)事非。”數(shù)與形是現(xiàn)實(shí)世界中客觀事物的抽象和反映，同時(shí)也是我們的數(shù)學(xué)的基石。“數(shù)”主要指實(shí)數(shù)、復(fù)數(shù)或代數(shù)對(duì)象及其關(guān)系，屬于數(shù)學(xué)抽象思維范疇，是人的左腦思維的產(chǎn)物。而“形”主要指幾何圖形，屬于形象思維范疇，是人的右腦思維的產(chǎn)物，數(shù)形結(jié)合使人充分運(yùn)用左、右腦的思維功能，相互依存、彼此激發(fā)，全面、協(xié)調(diào)、深入發(fā)展人的思維能力。我們認(rèn)為，數(shù)形結(jié)合，主要指的是數(shù)與形之間的一一對(duì)應(yīng)關(guān)系。數(shù)形結(jié)合就是把抽象的數(shù)學(xué)語(yǔ)言、數(shù)量關(guān)系與直觀的幾何圖形、位置關(guān)系結(jié)合起來(lái)，通過(guò)“以形助數(shù)”或“以數(shù)解形”即通過(guò)抽象思維與形象思維的結(jié)合，可以使復(fù)雜問(wèn)題簡(jiǎn)單化，抽象問(wèn)題具體化，從而達(dá)到優(yōu)化解題途徑的目的。數(shù)形結(jié)合思想方法能巧妙地實(shí)現(xiàn)數(shù)與形之間的互換，使得看似無(wú)法解決的問(wèn)題簡(jiǎn)單化、明朗化，讓人有“山重水復(fù)疑無(wú)路，柳暗花明又一村”的感覺(jué)。數(shù)形結(jié)合思想方法在解題中的重要性決定了它在平時(shí)的教學(xué)中也應(yīng)該受到重視。在數(shù)學(xué)教學(xué)中教師要有意識(shí)地溝通數(shù)與形之間的聯(lián)系，幫助學(xué)生逐步樹(shù)立起數(shù)形結(jié)合的觀點(diǎn)，提高主動(dòng)應(yīng)用的意識(shí)，并使這一觀點(diǎn)扎根到學(xué)生的認(rèn)知結(jié)構(gòu)中，成為運(yùn)用自如的思想觀念和思維工具，從而提高學(xué)生的數(shù)學(xué)修養(yǎng)與解題能力。而在小學(xué)數(shù)學(xué)教學(xué)中，如果能突出數(shù)形結(jié)合思想，那將非常有利于學(xué)生從不同的側(cè)面加深對(duì)問(wèn)題的認(rèn)識(shí)和理解，提供解決問(wèn)題的方法，也有利于培養(yǎng)學(xué)生將實(shí)際問(wèn)題轉(zhuǎn)化為數(shù)學(xué)問(wèn)題的能力。

案例一：

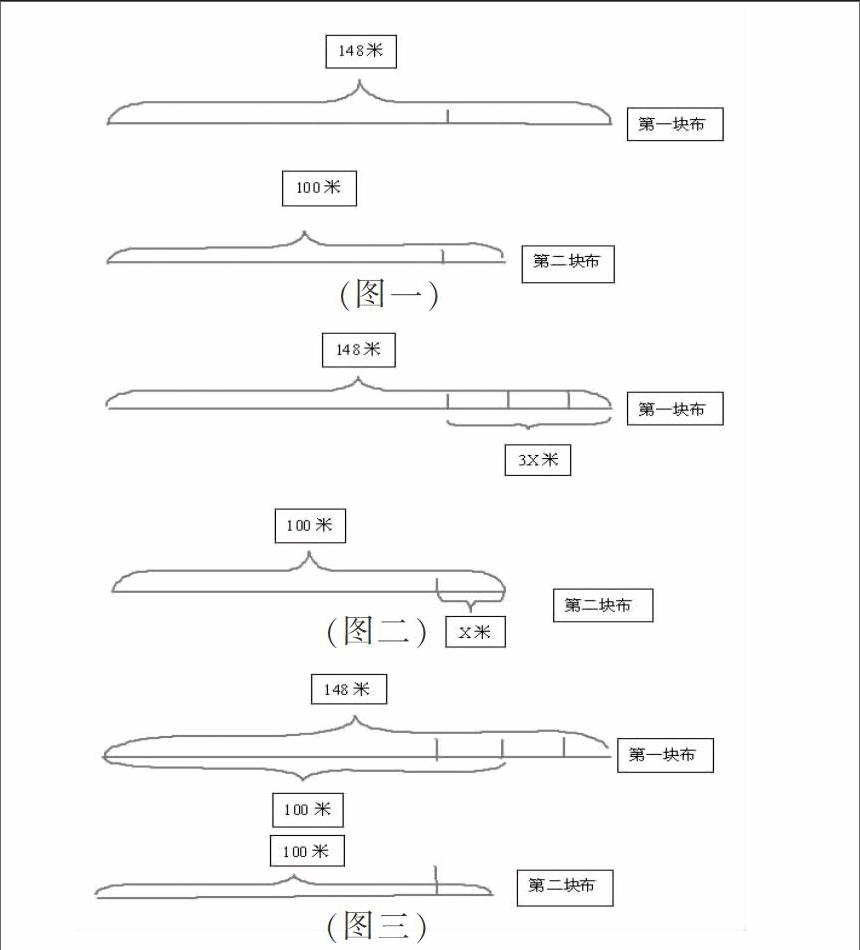
筆者在六年級(jí)一次授課過(guò)程遇到這么一道題：“有兩塊布料，第一塊長(zhǎng)148米，第二塊長(zhǎng)100米。兩塊布料各剪去同樣長(zhǎng)的一段后，第一塊剩下的長(zhǎng)度是第二塊的3倍，兩塊布料各剩下多少米？”當(dāng)時(shí)全班學(xué)生炸開(kāi)了鍋。生1：“這道題沒(méi)法解，不告訴我們剪去多少米就不知道剩下的米數(shù)”生2反駁道：“那還叫你求，不如回到一年級(jí)去讀。”生3（慢條斯理）：“你兩別爭(zhēng)，用我們已學(xué)過(guò)的方程知識(shí)來(lái)解答準(zhǔn)行。”生4：“那該設(shè)誰(shuí)為x米？”很多學(xué)生隨聲應(yīng)和。這時(shí)刻我相機(jī)說(shuō)道：“同學(xué)們?cè)僬J(rèn)真把題目讀兩遍，找找看，準(zhǔn)能找出題中相等的數(shù)量關(guān)系。”經(jīng)我這么一提醒，班級(jí)頓時(shí)安靜下來(lái)，學(xué)生陷入思考中。生5：“應(yīng)該設(shè)第二塊布剩下部分為x米，得到方程為100-x=148-3x.”生6：“我知道這個(gè)方程兩邊的數(shù)量關(guān)系，但我們沒(méi)解過(guò)這種方程不知道怎樣解。”全班大約有的學(xué)生站起來(lái)說(shuō)：“對(duì)！只會(huì)列式不會(huì)解！”我笑著回答：“同學(xué)們先別急，你們想想看，列方程解決問(wèn)題除了要找數(shù)量關(guān)系外，我們還可以請(qǐng)什么來(lái)幫忙？”生齊答：“畫(huà)線段圖。”此時(shí)，我順?biāo)浦劢M織全體學(xué)生根據(jù)題意畫(huà)出線段圖：

引導(dǎo)學(xué)生從圖一認(rèn)真觀察到圖三，生7：“3x-x=148-100.”就這樣，一道學(xué)生不會(huì)解答的問(wèn)題在我的組織下迎刃而解。

案例二：

小學(xué)數(shù)學(xué)新課標(biāo)提出：“學(xué)生應(yīng)當(dāng)有足夠的時(shí)間和空間經(jīng)歷觀察、實(shí)驗(yàn)、猜測(cè)、計(jì)算、推理、驗(yàn)證等活動(dòng)過(guò)程。”國(guó)標(biāo)蘇教版教材六年級(jí)上冊(cè)第18頁(yè)第9題：“學(xué)校科技館大門(mén)前有5級(jí)臺(tái)階，每級(jí)臺(tái)階長(zhǎng)6米，寬0.3米，高0.2米。（1）5級(jí)臺(tái)階一共占地多少平方米？（2）給這些臺(tái)階鋪上地磚，至少需要鋪多少平方米地磚？”解答第（1）個(gè)問(wèn)題學(xué)生沒(méi)有疑義，在解答第（2）個(gè)問(wèn)題時(shí)，學(xué)生爭(zhēng)議很大。生1：臺(tái)階兩旁是否有其他建筑？生2：臺(tái)階是一旁靠建筑還是獨(dú)立呈現(xiàn)？生3：照你倆的想法（指著前面兩位學(xué)生）我認(rèn)為本題有3種答案：第一臺(tái)階兩旁被其他建筑物包圍不用貼瓷磚；第二臺(tái)階一旁被建筑物包圍，另一旁裸露的；第三臺(tái)階兩旁都裸露著。我并沒(méi)有打斷他的發(fā)言，而是肯定了她的想法并給予及時(shí)表?yè)P(yáng)：“你真是個(gè)有心人，在我們的校園內(nèi)就存在著這三種情況的臺(tái)階，第一種情況是在教學(xué)樓與行政樓之間的臺(tái)階；第二種情況是在要去行政樓二層的戶(hù)外小臺(tái)階；第三種情況是在廁所前的長(zhǎng)臺(tái)階。課后老師與你們一起去看看核實(shí)這三種情況，好嗎？”課后，我?guī)ьI(lǐng)全班學(xué)生到該三處地方一起觀察，幫助學(xué)生解決課中產(chǎn)生的疑惑。