基于數值積分的變位儲油罐罐容表標定的改進算法

侯國亮，李希瑞，孫　敏，林泳坤

(1.長春師范大學數學學院，吉林長春 130032；2.長春師范大學工程學院，吉林長春 130032)

?

基于數值積分的變位儲油罐罐容表標定的改進算法

侯國亮1，李希瑞2，孫敏2，林泳坤2

(1.長春師范大學數學學院，吉林長春 130032；2.長春師范大學工程學院，吉林長春 130032)

[摘要]本文采用細化積分區域的方法給出了標定變位儲油罐罐容表的數值積分新算法，該算法克服了文獻[1]中所提算法在油面高度較低時計算誤差大的缺點。數值實驗表明，本文所提算法正確有效。

[關鍵詞]細化積分區域；數值積分；罐容表；變位儲油罐

1問題背景介紹

通常加油站都有若干個儲存燃油的地下儲油罐，并且一般都有與之相配套的“油位計量管理系統”，采用流量計和油位計來測量進、出油量與罐內油位高度等數據，通過預先標定好的罐容表(即罐內油位高度與儲油量的對應關系)進行實時計算，以得到罐內油位高度和儲油量的變化情況.

許多儲油罐在使用一段時間后，由于地基變形等原因，就可能會使罐體的位置發生縱向傾斜和橫向偏轉等變化(以下稱之為變位)，從而導致罐容表發生改變.按照有關規定，需要定期對罐容表進行重新標定.圖1是一種典型的儲油罐尺寸及形狀示意圖，其主體為圓柱體，兩端為球冠體，圖2是其罐體發生縱向傾斜變位的示意圖，圖3是罐體發生橫向偏轉變位的截面示意圖.

現階段，變位儲油罐罐容表的標定工作均是由人工或半人工操作實現的.需要在加油站停工條件下進行，而且操作程序繁瑣復雜，技術要求嚴格，時間周期長，這樣做既影響加油站的正常運轉，也需要較高的經濟成本，同時還會有一定的系統誤差和測量誤差.為此，運用記錄的儲油罐進、出油量的實際數據，進行建模分析，正確識別罐體變位參數，實時修正罐容表，將是一項非常有現實意義的研究課題.

圖1　儲油罐正面示意圖

圖3　儲油罐截面及坐標系示意圖

針對該問題，文獻[1]運用坐標旋轉變換、示性函數和Matlab中計算重積分的程序來計算任意變位后的罐內油量與油面高度，大大簡化了繁瑣的數學推導過程①，是解決該問題的一種實用算法，值得推廣.但該方法的一個致命缺點是當變位儲油罐內油面高度較低時計算的罐內油量與油面高度相對應的數據誤差較大，因此如何克服此缺點就成了此方法是否能得到廣泛推廣應用的一個關鍵性問題.本文在深入分析該法的計算程序基礎之上，采用細化積分區域的方法，提出了此法的改進算法程序，成功地克服了該致命缺點.數值實驗表明，新算法正確有效，為該類方法的實際推廣應用奠定了扎實的基礎.

2算法的理論分析

2.1坐標系的建立

建立固連于油罐并隨油罐一起轉動的空間直角坐標系，以油罐中心為坐標原點，中央橫截面為xOy平面，x軸、y軸的正方向如圖3(a)所示，z軸正方向由右手定則確定，即沿中軸線方向，如圖1所示. 規定，如無特別說明，下文中涉及的區域及其約束條件的數學表達式均是在此坐標系下得到的.

2.2積分區域的確定

依據多重積分的幾何意義可知，對罐內油量所占據的空間區域進行積分即可得到油的體積.該問題中所涉及的積分區域受兩類條件約束，一是油罐外殼的約束，二是油面所在平面的約束.其中，油罐外殼約束可表述為

其中，r=1.5m，R表示油罐兩端的球冠所在的球面半徑，S表示坐標原點到球冠所在的球面球心的距離.下面討論儲油罐發生變位后油面所在平面的數學表達式.為了敘述的方便，規定儲油罐發生縱、橫向變位時的兩個轉角按逆時針轉動時為正，如圖4所示.

圖4　轉角示意圖

根據相對運動的思想，當儲油罐繞x軸轉動α角、繞z軸轉動角β時，我們可以設想成儲油罐未動，而是罐內實際油面所在的平面以油浮子所在位置(0，h-r，2)為定點，繞x軸轉動了-α角，繞z軸轉動了-β角，其中h表示儲油罐“油位計量管理系統”顯示的油位高度.這種等效轉化的思想能在不影響體積計算的前提下，使得關于積分區域約束條件的討論大幅簡化.接下來，本文就運用這種思想給出油面所在的平面以油浮子所在位置(0，h-r，2)為定點，繞x軸轉動-α角、繞z軸轉動-β角后所得對應平面的數學表達式.

首先，由坐標變換相關知識可求出繞x軸轉動-α角，繞z軸轉動-β角的變換矩陣.設變換前點的坐標為(ξ，η，ζ)，變換后點的坐標為(x，y，z)，則繞x軸轉動-α角的變換可表述為

繞z軸轉動-β角的變換為

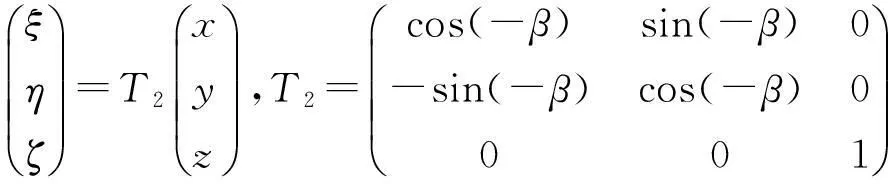
一般來說，繞定點轉動物體的有限角位移具有不可交換性，但由于該問題中所涉及的轉動角α、β均很小，以至于變位次序對變位后的結果幾乎沒有影響，所以，旋轉前的點(ξ，η，ζ)與旋轉后的點(x，y，z)之間的關系可表示為

或T=T2T1均可.按T=T1T2展開得

η=xcosαsinβ+ycosαcosβ-zsinα.

代入η=0即可得由xOz坐標平面繞x軸旋轉-α角，并再繞z軸旋轉-β角后所得對應平面的數學表達式為

Γ：xcosαsinβ+ycosαcosβ-zsinα=0.

其次，若把此時罐內油面所在的平面按照上述要求旋轉后的平面記為平面Η，則平面Η與平面Γ平行，區別在于平面Η經過油浮子所在的位置，即油浮子所表示的點在平面Η上，所以平面Η的方程可表述為

xcosαsinβ+ycosαcosβ-zsinα=C.

其中，C為一常數.若將油浮子坐標(0，h-r，2)代入，即可得

C=(h-r)cosαcosβ-2sinα.

所以按要求轉動后油面所在的平面方程為

Η：xcosαsinβ+ycosαcosβ-zsinα=(h-r)cosαcosβ-2sinα.

而油總是位于平面Η的下面，所以積分區域可表示為

3數值實驗

在該部分，我們主要運用Matlab函數triplequad給出基于積分區域

的標定變位儲油罐罐容表的數值積分算法程序.

若定義關于積分區域D的示性函數為

則儲油罐內油的體積V(m3)與旋轉角度α、β及儲油罐“油位計量管理系統”顯示的油位高度h(m)之間的關系可表示為

其中，積分區域E為能包含區域D的最小區域.

文獻[1]中的標定變位儲油罐罐容表的數值積分算法就是根據上述理論提出的，該方法避開了傳統積分方法對積分上下限的繁瑣討論(參見文獻[7]).當變位儲油罐內油面較高時，用該算法標定變位儲油罐罐容表誤差小、精度高；但當變位儲油罐內油面較低時，用該方法標定變位儲油罐罐容表誤差大，具體情況詳見表1中相對應的數值結果.本文通過細化積分區域的途徑，給出了基于上述理論的標定變位儲油罐罐容表的數值積分新算法，該算法是文獻[1]中所提算法的改進，能夠很好地克服原算法的不足，相關的數值表現如表1所示.

表1　相關算法的部分數值實驗數據

橫向續表

橫向續表

橫向續表

注：表1中第一行所列數據是變位儲油罐自帶系統顯示的油位高度，單位為m；第二行的所有數據是根據文獻[7]中所給方法編程(qingxie200.m)算出的變位儲油罐內不同油位高度時對應的油量容積，單位是m2，因該方法是用繁瑣的傳統積分方法得到的，故所得的數據可作為用以衡量其它方法好與劣的標準數據指標；第三行所列數據是運用文獻[1]中所提的數值積分算法編程(qingxie210.m)計算的；而第四行里的所有數據是用本文所給的數值積分改進算法編程(qingxie211.m)算出的.

從表1所列數據不難看出，當變位儲油罐內油量較少時，即罐內油位高度很低時，用文獻[1]中所給的數值積分算法標定變位儲油罐罐容表時誤差大，而用本文所提的數值積分改進算法可以很好地解決該問題.當然，對于變位儲油罐內油量很足時，即罐內油位高度不低時，這兩個方法均能對變位儲油罐罐容表進行很好的修正.

文中所涉及的主要算法的實現程序碼：

qingxie211.m

r=1.5;R=1.625;s=5-R;a=(2.11*pi)/180; b=(4.31*pi)/180; ta=sin(a)/cos(a); ct=cos(a)/sin(a); h=zeros(1,31); V=zeros(1,31);

for i=1:31

h(i)=0.1*(i-1);

if h(i)<=6*ta

zc=2-h(i)*ct*cos(b); bd=(5-zc)*ta-r;

V(i)=triplequad(@(x,y,z)(x*cos(a)*sin(b)+y*cos(a)*cos(b)-z*sin(a)<=cos(a)*cos(b)*(h(i)-r)-2*sin(a)).*(x.^2+y.^2<=r^2).*(z>=-s-sqrt(R^2-x.^2-y.^2)).*(z<=s+sqrt(R^2-x.^2-y.^2)),-r,r,-r,bd,zc,5);

elseif h(i)<=1.5-3*ta

be=h(i)+3*ta-1.5;

V(i)=triplequad(@(x,y,z)(x*cos(a)*sin(b)+y*cos(a)*cos(b)-z*sin(a)<=cos(a)*cos(b)*(h(i)-r)-2*sin(a)).*(x.^2+y.^2<=r^2).*(z>=-s-sqrt(R^2-x.^2-y.^2)).*(z<=s+sqrt(R^2-x.^2-y.^2)),-r,r,-r,be,-5,5);

else

V(i)=triplequad(@(x,y,z)(x*cos(a)*sin(b)+y*cos(a)*cos(b)-z*sin(a)<=cos(a)*cos(b)*(h(i)-r)-2*sin(a)).*(x.^2+y.^2<=r^2).*(z>=-s-sqrt(R^2-x.^2-y.^2)).*(z<=s+sqrt(R^2-x.^2-y.^2)),-r,r,-r,r,-5,5);

end

end V

qingxie210.m

r=1.5;R=1.625;s=5-R;a=(2.11*pi)/180; b=(4.31*pi)/180;

h=zeros(1,31); V=zeros(1,31);

for i=1:31

h(i)=0.1*(i-1);

V(i)=triplequad(@(x,y,z)(x*cos(a)*sin(b)+y*cos(a)*cos(b)-z*sin(a)<=cos(a)*cos(b)*(h(i)-r)-2*sin(a)).*(x.^2+y.^2<=r^2).*(z>=-s-sqrt(R^2-x.^2-y.^2)).*(z<=s+sqrt(R^2-x.^2-y.^2)),-r,r,-r,r,-5,5);

end V

qingxie200.m

r=1.5; R=1.625; a=(2.11*pi)/180; b=(4.31*pi)/180; si=sin(a);cs=cos(a);

ta=si/cs;ct=cs/si; h=zeros(1,31); V=zeros(1,31);

for m=1:31

h(m)=0.1*(m-1); H=(h(m)-r)*cos(b)-2*ta;

if H<=(4*ta-r)

xA=3.375*si*cs+H*cs^2+si*sqrt(R^2-(3.375*si+H*cs)^2);

xB=H+4*ta; V1=quad(@g3,xB,xA,[],[],H,ct); V2=quad(@g4,-1.5,xB);

V(m)=2*quad(@g1,xB,xA,[],[],H,ct)+2*quad(@g2,-1.5,xB,[],[],H,ct)+2*V1+2*V2;

else

xA=3.375*si*cs+H*cs^2+si*sqrt(R^2+(3.375*si+H*cs)^2); xB=H+4*ta; xC=H-4*ta; xD=-3.375*si*cs+H*cs^2+si*sqrt(R^2-(3.375*si-H*cs)^2);

V3=quad(@f2,xB,xA,[],[],H,ct); V4=quad(@g4,xC,xB);

V5=quad(@g4,-1.5,xC); V6=quad(@f3,xD,xC,[],[],H,ct);

V(m)=2*quad(@g1,xB,xA,[],[],H,ct)+2*quad(@g2,xC,xB,[],[],H,ct)+13.5*

quad(@f4,-1.5,xC)-2*quad(@f1,xD,xC,[],[],H,ct)+2*V3+2*V4+4*V5-2*V6;

end end

for n=1:31 V(n)=real(V(n)); end V

function y=f1(x,H,ct) %以下8個函數為程序qingxie200.m中的調用函數

y=((x-H)*ct+3.375).*sqrt(1.625^2-x.^2-((H-x)*ct-3.375).^2);

function y=f2(x,H,ct)

y=0.5*sqrt(1.625^2-x.^2-((H-x)*ct+3.375).^2).*sqrt(((H-x)*ct+3.375).^2)+0.5*(1.625^2-x.^2).*asin(sqrt((1.625^2-x.^2-((H-x)*ct+3.375).^2)./(1.625^2-x.^2)));

function y=f3(x,H,ct)

y=0.5*sqrt(1.625^2-x.^2-((H-x)*ct-3.375).^2).*sqrt(((H-x)*ct-3.375).^2)+0.5*(1.625^2-x.^2).*asin(sqrt((1.625^2-x.^2-((H-x)*ct-3.375).^2)./(1.625^2-x.^2)));

function y=f4(x) y=sqrt(2.25-x.^2);

function y=g1(x,H,ct)

y=((H-x)*ct+3.375).*sqrt(1.625^2-x.^2-((H-x)*ct+3.375).^2);

function y=g2(x,H,ct) y=((H-x)*ct+3.375).*sqrt(2.25-x.^2);

function y=g3(x,H,ct)

y=0.5*sqrt(1.625^2-x.^2-((H-x)*ct+3.375).^2).*sqrt(((H-x)*ct+3.375).^2)+0.5*(1.625^2-x.^2).*asin(sqrt((1.625^2-x.^2-((H-x)*ct+3.375).^2)./(1.625^2-x.^2)));

function y=g4(x)

y=0.5*sqrt(2.25-x.^2).*sqrt(1.625^2-2.25)+0.5*(1.625^2-x.^2).*asin(sqrt((2.25-x.^2)./(1.625^2-x.^2)));

[注 釋]

①文獻[7]中所提的解決方法即是用繁瑣的多元微積分知識獲得的，但此法的計算精度高，穩定性、通用性好。本文數值實驗部分的標準數據即是用該方法編程計算得到的。

[參考文獻]

[1]姜亞中,淡志強,呂曉帆,等.基于數值積分的儲油罐的變位識別與罐容表標定[J].工程數學學報,2010,27(Supp.1): 39-46.

[2]姜啟源,謝金星,葉俊.數學建模[M].3版.北京:高等教育出版社,2003.

[3]韓中庚.數學建模方法及其應用[M].2版.北京:高等教育出版社,2009.

[4]劉仁云,張曉麗,侯國亮.數學建模方法與數學實驗[M].北京:中國水利水電出版社,2011.

[5]同濟大學數學系.高等數學(下冊)[M].7版.北京:高等教育出版社,2014.

[6]蘇金明,阮沈勇.MATLAB實用教程[M].北京:電子工業出版社,2005.

[7]韓中庚,杜劍平.儲油罐的變位識別與罐容表標定模型[J].工程數學學報,2010,27(Supp.1):92-102.

Improved Algorithm of Calibration of Capacity Table of Oil Tank of Deflection Based on Numerical Integration

HOU Guo-liang1, LI Xi-rui2, SUN Min2, LIN Yong-kun2

(1.School of Mathematics, Changchun Normal University, Changchun Jilin 130032, China;2.School of Mechanical Engineering, Changchun Normal University, Changchun Jilin 130032, China)

Abstract:In this paper, using the approach of subdividing domain of integration a new algorithm of Calibration of Capacity Table of oil tank of deflection is proposed. This new algorithm is based on numerical integration and overcomes the drawback of the large error of calculation that arises from the algorithm’s applications presented in the literature [1]. Preliminary numerical results indicate that the method given in this paper is correct and efficient.

Key words:subdividing domain of integration; numerical integration; capacity table of oil tanks；oil tank of deflection

[作者簡介]侯國亮(1981- )，男，講師，博士研究生，從事計算數學可信驗證、數值代數研究。

[基金項目]國家級大學生創新創業訓練計劃項目“建模分析儲油罐的變位識別與罐容表標定”(201410205020)。

[收稿日期]2015-11-17

[中圖分類號]O151；O24

[文獻標識碼]A

[文章編號]2095-7602(2016)02-0001-06