水輪機葉片翼型參數化研究概述

朱堯華，袁壽其，張金鳳，方玉建(江蘇大學國家水泵及系統工程技術研究中心，江蘇 鎮江 212013)

0 引 言

中國水電的發展從20世紀初的云南石龍壩電站到現在已經走過了100多年的歷程。圖1中展現了建國以后不同年代水電的裝機容量和年發電量[1,2]。圖1中標識了1960年我國自主設計的第一座水電站-新安江水電站；2004年隨著公伯峽電站1號機組的投產，我國裝機總量突破1億kW，躍居為世界水電第一大國；如今水電的裝機容量達到3.33億kW。尤其近20年來，由于國家對大力發展水電事業的支持，特別是“西部大開發”國家戰略，水電的發展可以說是處在蓬勃的發展時期，而且，這樣的態勢還將延續很長一段時期。

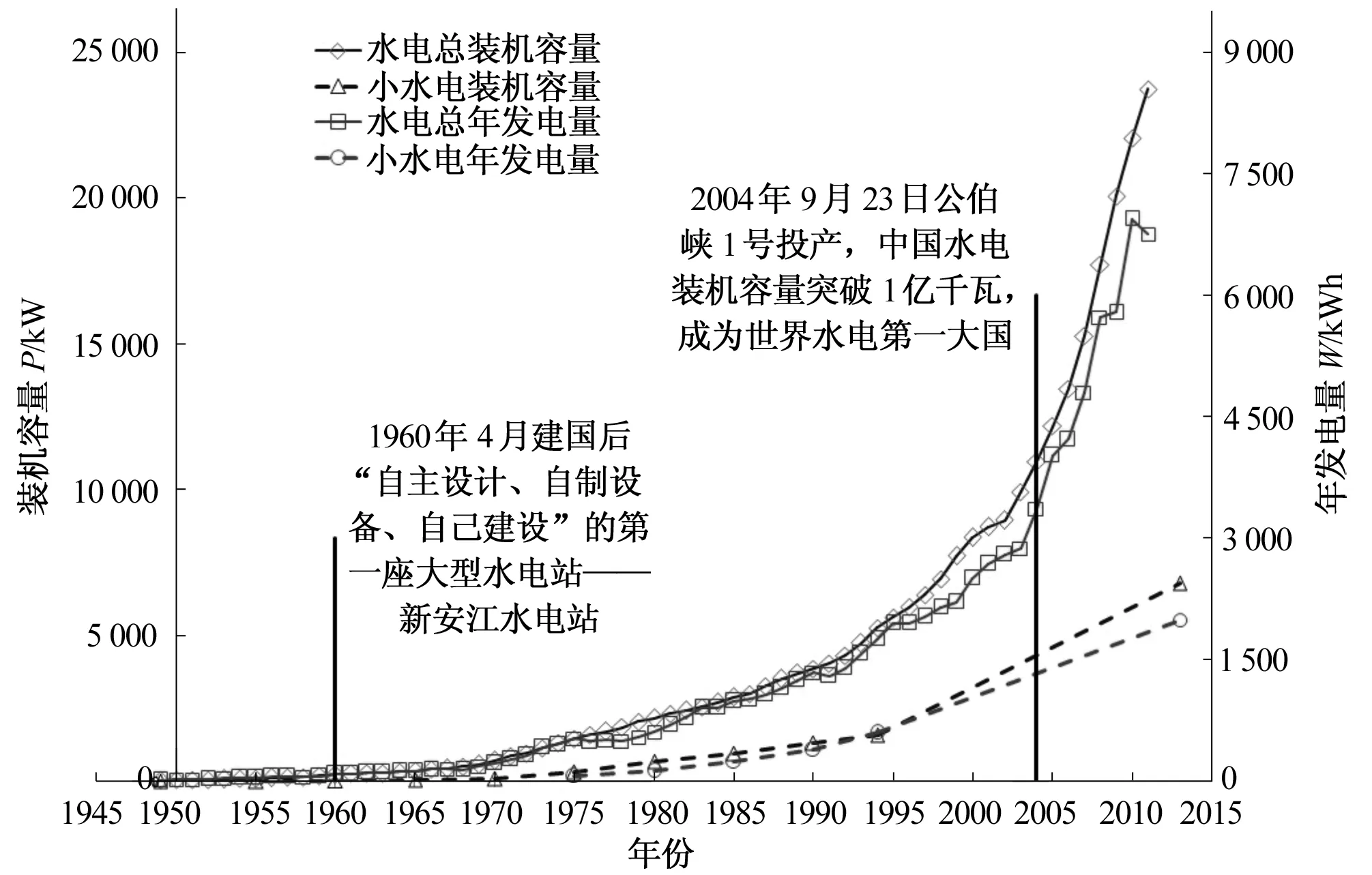
圖1 我國水電發展歷程圖Fig.1 Hydropower development process in China

雖然我國水電事業發展迅速，但是水輪機設計開發的方法并不能匹配現如今水電的快速發展。傳統的水力設計和開發是根據具體電站的參數和要求，每個項目都是從零開始做設計，然后進行大量的優化，包括設計和制作許多模型進行大量的模型試驗，最終篩選出最優的水力模型。

隨著經驗的積攢以及一些優秀的水力模型的成功開發，尤其是計算機技術在幾何造型、CFD計算、有限元計算方面的快速發展與成熟，并在流體機械中獲得大量成功的應用，就出現了現代的水輪機的設計方法：根據項目具體參數要求和廠家已開發的水力模型進行初步水力分析，選擇出適合作為進一步水力開發的基礎模型，創建幾何模型，采用計算流體模擬(CFD計算)和有限元分析(靜態、動態應力和變形分析)聯合進行優化。這個過程與傳統的方法相比，它充分利用計算機技術實現優化的過程，取代了大量耗時投資大的模型制造和試驗成本，具有很大的優勢。即使如此，CFD模擬也不能代替模型試驗，往往對于大型項目，還是需要開發設計1～3個模型進行試驗篩選。

基于計算機的水力優化是從水力性能的角度去優化，包括效率、空化和壓力脈力及其分布、動態應力及其分布和變形控制等方面的特性。但所有的優化計算，歸根結底都是對轉輪或模型幾何形狀的優化。

總之，具備一個高效的轉輪葉片翼型和幾何優化或參數化控制的方法，是實現這個水力和結構聯合優化獲得成功應用的核心。因此，對葉片翼型進行直接參數化的幾何設計就有著重要的意義。

1 國內外發展現狀

1.1 曲線的參數化思想

對于一般曲線的參數化設計理念，1988年M. Cardew-Hall等[3]提出完整的一般曲線參數化設計流程，即定義曲線→生成路徑→計算曲線→創建模型→選取方案→反饋設計。國內在2002年金建國[4]等介紹了一般曲線參數化的各個模塊及它們之間的內在聯系。隨后，金建國等[5]又提出了實現曲線參數化的6個基本要素，即曲線的分類，曲線尺寸的提取研究，曲線基本約束關系的歸納以及約束的語言文法表示，曲線、曲面的幾何拓撲網狀結構表示，約束的求解與幾何推理和約束關系的滿足方法。

對于具體的曲線參數化方法，2008年蔡江畔等[6]分別采用B樣條曲線和參數3次樣條曲線描述離心泵前后蓋板、軸面流線和流線展開線，改變了傳統手工設計方法，實現了計算機化。2011年張海軍等[7]在飛艇外形設計過程中，采用了3種參數化方法：Bezier，B樣條和NURBS。3種參數化方法在形式上基本相同，都包含基函數和控制點兩部分；不同點是基函數的形式以及基函數中的變量取值范圍不同。由于NURBS曲線多一組加權系數，增強了控制點對局部曲線形狀的影響，故NURBS曲線擬合性能和效率都高于其他兩種方法。

1.2 傳統參數化方法應用于葉片翼型設計

水輪機葉片傳統的設計方法主要有3種：升力法，保角變換法和奇點分布法[8]。相比較而言，奇點分布法[9]是應用相對廣泛的一種參數化設計方法，它是用集中或者連續分布的渦、源、匯等奇點代替葉型。傳統的參數化方法應用與葉片翼型設計優化中，主要是國內學者的一些研究。2009年薛正福等[10]在風力機適應性葉片中采用程序驅動法，利用了ANSYS APDL 參數化建模，通過分析模型的幾何特點，確定了模型的主參數以及各尺寸間的數學關系。2010年朱國俊等[11]開發了基于奇點分布法和Bezier曲線參數造型方法的軸流式水輪機平面葉柵設計方法。先采用奇點分布法設計出翼型骨線并將骨線用Bezier曲線參數化，這樣可以通過控制參數來變化骨線形狀，然后把優秀翼型的厚度疊加到骨線上，這樣就形成了通過控制參數的變化來變化葉柵翼型。2012年崔濤[12]用Bezier曲線參數化葉片翼型骨線，然后將導葉直接加到初始葉片進口前的流道上，保證了實際流動中轉輪來流的真實條件?？紤]葉片進出口邊分別在軸向和周向上變化，多加了4個變量進行優化。2012年嚴敬等[13]將儒可夫斯基變換函數應用到軸流葉輪葉片的翼型設計中，以計算好的圓弧為骨線，采用被廣泛應用的性能良好的791翼型加厚程序，最終得到流面完整翼型。2013年張為民等[14]運用NURBS進行翼型模板的定義，基于翼型模板的葉片參數化設計方法，根據葉片翼型弦長、安放角、葉片半徑、翼型模板等參數進行葉片翼型數據的自動計算，求得各截面控制頂點的實際坐標；運用UG/open API 模塊開發了葉片設計系統，實現了葉片設計的參數化。

1.3 整體參數化方法應用于葉片翼型設計

不同于傳統的參數化設計葉片翼型的方法將參數化應用于翼型骨線等，近年來也有一些將參數化方法直接應用到葉片翼型的外形輪廓，然后，通過各類不同的求解方法(包括神經網絡算法和遺傳算法等)可以求得翼型輪廓的最優解。這樣，可以采用有限數量的控制點坐標表征葉片翼型，對翼型的外形進行整體的控制，進而在今后的優化改進過程中僅需要改變控制點坐標實現改變葉片翼型的形狀的作用。2003年M S Floater[15]提出并分析了一種無網格參數化的方法，這種方法基于評估曲線曲面的參數化方法，將一些無順序點的樣本重新建成一條曲線。 2007年I M Valakos等[16]指出差分進化算法用于優化的離心葉輪的背面幾何形狀，計算出的最大應力，以延長其超速極限。而背面的幾何形狀是使用Bezier曲線定義它的參數，并以此作為設計變量，用于現有優化程序。2010年閔新勇等[17]運用商業軟件HyperWorks中HyperMorph模塊的網格變形功能實現基于網格變形的翼型參數化。2010年Liang Y等[18]提出使用NURBS參數化方法設計多目標穩固翼型，并且對NASA SC0712翼型進行參數化設計，提升了翼型的氣動性能。2011年Y Dong等[19]提出了一種簡單而有效的逆設計方法，用于調整某些幾何參數建立的葉片模具輪廓。2012年K Heinze等[20]提出了一種在設計過程中，采用概率方法來考慮壓縮機葉片的幾何偏差，根據氣流的流線計算以下參數：前緣的軸向位置、前緣的切線位置、交錯角、弦長、最大彎度及弦上位置、最大厚度及弦上位置、前緣厚度及弦上位置和后緣厚度及弦上位置。2012年李文全等[21]利用 Bezier 曲線對軸流泵葉片翼型坐標點進行曲線擬合，反求 Bezier 曲線控制點，從而可得各相應翼型曲線。2012年A Kharal等[22]指出基于Bezier-PARSEC 3434參數化方法和3種人工神經網絡方法，使用15個參變量，采用基因算法對翼型進行造型，得到翼型的壓力系數分布。2013年C B Allen等[23]提出懸停直升機旋翼的氣動外形優化，利用可壓縮CFD空氣動力學模型，用作表面控制和變形的主要要素的外形參數化方法，鏈接到徑向基函數全局插值，以提供主要要素運動的直接傳遞到設計表面和CFD體網格的變形，因此幾何體的控制和體網格變形問題同時解決。2013年S. Walton等[24]比較了一些自由梯度算法，最終提出使用布谷鳥搜索算法對翼型和網格進行優化。2013年Q Wang等[25]提出使用B樣條曲線對中等厚度的風機翼型后緣進行設計，并且使用改良的粒子群優化算法對翼型進行整體造型。2014年R Mukesh等[26]提出基于PARSEC參數化方法僅使用12個參數對航空翼型NACA2411進行設計，并且使用遺傳算法對設計的翼型進行優化設計。2014年P D Vecchia等[27]在PARSEC 參數化翼型過程中以納什平衡為目標采用基因算法優化翼型，并且認為CFD計算時應當采用StarCCM+ 和OpenFOAM軟件。2014年Y V Pehlivanoglu[28]提出一種基于基因算法和神經網絡的機翼翼型的逆設計方法，縮短了計算時間，并且比較了6種不同的算法，最后得出新的設計方法S12-GA最有效。2014年K Heinze等[29]提出翼型可以使用Voronoi圖和Delaunay三角網參數化，并對水輪機葉片后緣骨線(圖2)以及翼型(圖3)進行參數化。2015年S Murugan[30]等在變彎度機翼的設計過程中，提出分級建模優化，采用多目標優化方法來滿足機翼的幾何外形和動力要求。

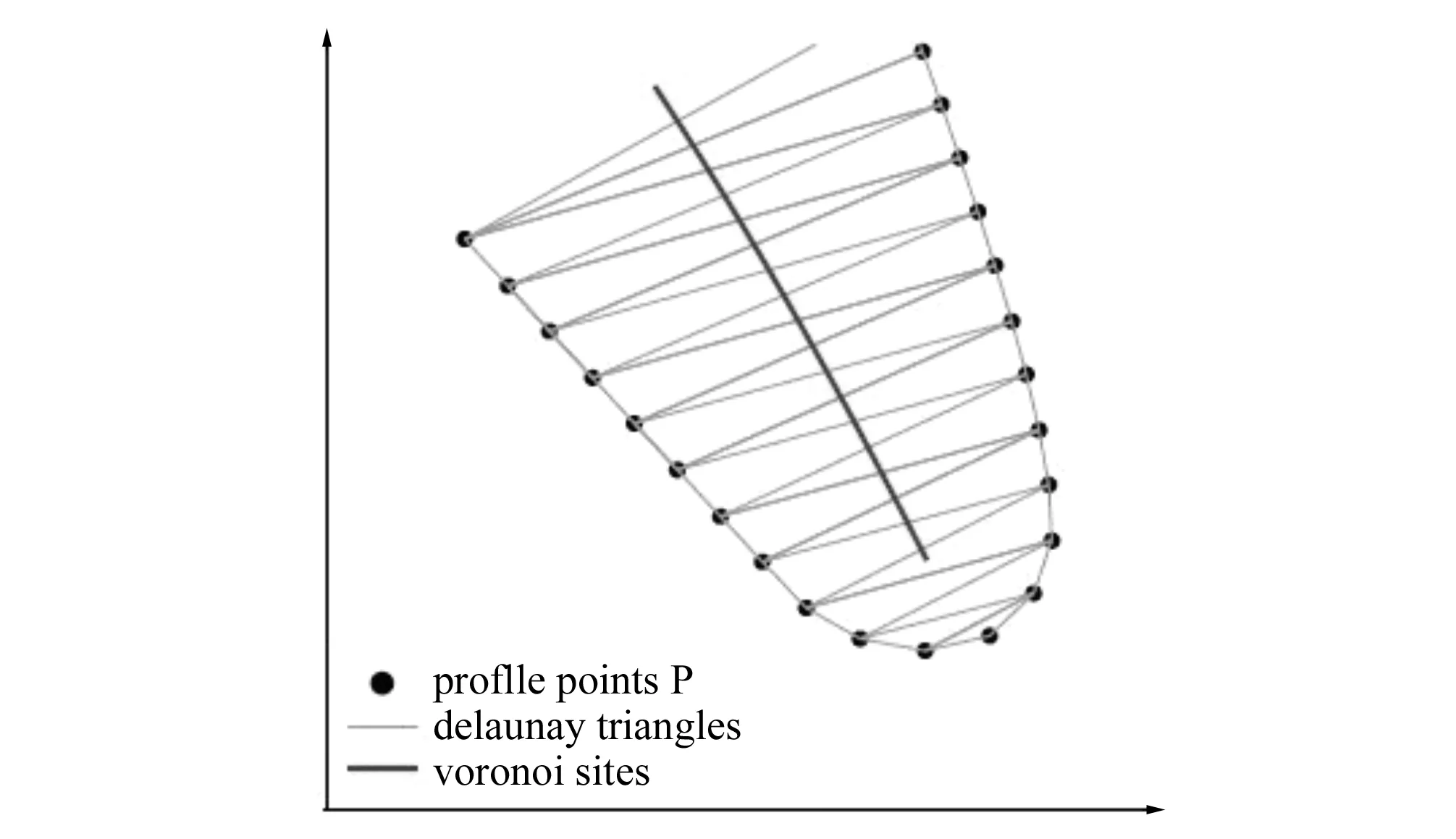
圖2 Voronoi圖(水輪機葉片后緣骨線)Fig.2 Voronoi graph (turbine blade trailing edge)

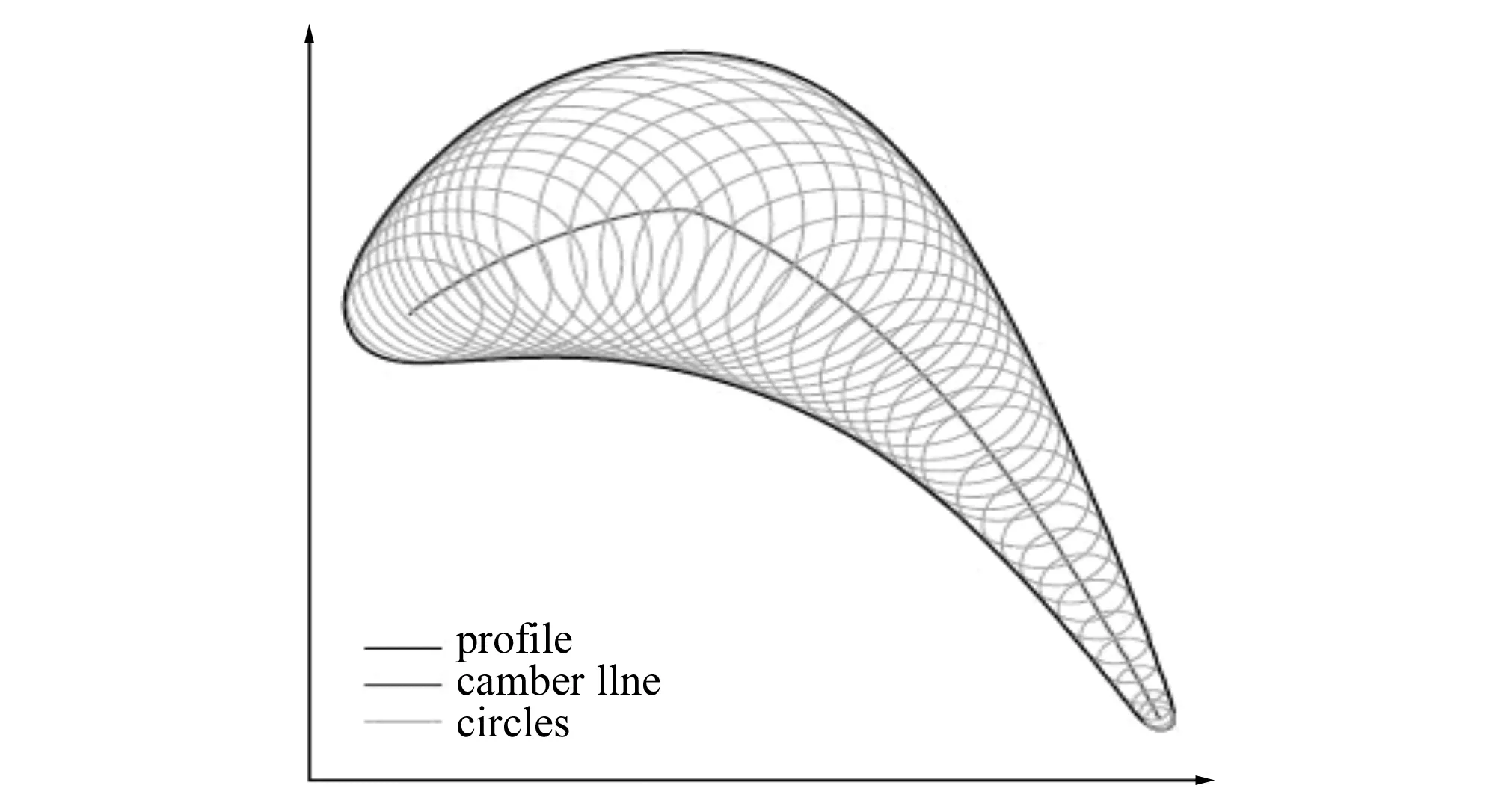
圖3 Delaunay三角網參數化Fig.3 Delaunay parametric triangulation

因此，綜上分析，可以得到以下結論。

(1)目前，隨著計算幾何學科的發展，對曲線參數化的研究已經非常成熟，尤其是在航空翼型方面出現了很多參數化設計優化方法。

(2)在水力機械領域，國內學者對曲線參數化進行了許多研究。從這些研究來看，主要是應用曲線參數化于具體的傳統水力設計和優化，即將選取優秀的加厚程序應用到參數化的骨線流面上。但將曲線和曲面參數化直接應用于翼型和葉片的優化較少，其核心的問題是對翼型和葉片的參數化造型研究還不夠深入和透徹。而由于整體參數化方法得到的結果在設計過程中已經進行初步的優化，并且由于參數數量有限，可以更容易通過改變參數進一步優化葉片翼型，所以國外學者在曲線參數化方面的研究更多，方法多種多樣。

2 采用整體參數化方法應用于水輪機葉片設計

曲線參數化思想在航空翼型，特別是現有翼型譜中翼型的分析比較多，得到的多是翼型的氣動性能，這是由于在氣體中，雷諾數相對較低，流動相對穩定，升阻比較大[31]。其中使用的主要有幾類重要的參數方法，Hicks-Henne型函數疊加法[32-34]和PARSEC幾何參數法[35-37]等。

水輪機葉片傳統的設計方法中應用最廣泛的奇點分布法分析設計葉片時，一般認為翼型的厚度很小，可以用葉型骨線代替翼型。在選定翼型最大厚度和翼型厚度沿骨線變化規律后，就可以在各翼型骨線上作各計算截面的翼型的剖面圖，即二維翼型圖，隨后，選定翼型轉動軸線，并按此把各計算截面翼型組成轉輪葉片。然而，奇點分布法在厚度較大的葉片的設計過程中，由于在設計過程中，葉型骨線代替翼型以及加厚程序的半經驗性，其設計過程存在一定的偏差。因此，今后的研究應更多的將曲線參數化的方法直接應用到水輪機葉片翼型的設計，用有限數量的參數控制翼型的外形，并且在確定控制點坐標的過程中采用優化算法選取最佳的解，得到的葉片翼型相對較好，再者，選用參數控制葉片翼型可以在優化過程中更加簡便的通過控制點坐標的變換實現幾何上的改變，達到優化的作用。

然而一般在水輪機葉片的設計過程中，由于水力性能的要求，很少采用單一翼型庫中的翼型，而是很多未知翼型的組合。因此分析水輪機葉片的過程中，需要從葉片中截取翼型進行參數化的分析。除了這些，在翼型的整體參數化造型中，還需要著重注意以下幾個問題。

2.1 控制點的選取

選取合適的控制點[38]是該方法的第一步，也是該方法最重要的一個環節?？刂泣c的選取直接關系到它的輪廓。一般參數化過程中，控制點坐標由翼型的特征變量(例如最大厚度及位置、最大隆起高度及位置等)來表征。當然，不同的方法得到的控制點也是不一樣的，但是，所有方法的目的相同，都是為了得到擬合度更高的曲線，圖4為由Bezier曲線參數化的某水輪機葉片翼型。

圖4 Bezier曲線參數化的某水輪機葉片翼型Fig.4 One Kaplan turbine airfoil parameterized by Bezier curve

2.2 方法的通用性

選取了一種參數化的方法，可能對這類翼型適用，然而，對于另外的不同形狀的翼型可能出現擬合度不高的情況，造成誤差較大，因此選取通用的翼型參數化方法，即通用的控制點，是該方法普遍適用的關鍵所在。一般而言，對于寬翼型擬合度較高的方法，而對于較窄的翼型擬合度較低。所以，選取通用的參數化方法是得到簡單易行的曲線輪廓的關鍵。

2.3 水力特性的比較

一般航空翼型的好壞由其氣動性能(如升阻比等)決定。而水輪機翼型不僅需要考慮升阻比等因素，更重要的是翼型生成的葉片的水力特性(如空化性能等)。一般情況下，參數化的方法雖然可以得到外形上與原翼型相似的輪廓，但是其水力性能與原翼型相比，還是會存在一定的偏差。由于水輪機葉片翼型最主要的還是其水力性能[39]，所以參數化的關鍵在于尋找簡單便捷的參數化方法的同時，保持或者優化翼型的水力性能。

3 結 語

采用曲線參數化的方法來設計葉片翼型，較傳統的設計方法，具有操作簡單，方便等特點，國內外對其的研究在航空領域已經比較成熟，但是在水力機械方面，參數化的思想還是相對落后，尤其在國內，想法思路已經出現，但是還是很多局限在以骨線為參數化的對象，通過加厚程序實現參數化建模，而真正把翼型輪廓作為參數化的對象目前還比較少。由于參數化的方法可以簡單地改變翼型葉片的形狀從而達到優化其水力性能的作用[40]，今后對葉片翼型結合參數化的研究，當然同時也要注意其與水輪機葉片相結合的問題，這樣才能為水輪機葉片優化設計的發展開拓新的方法。

□

[1] 邴鳳山. 中國水力發電年鑒(第16卷)[R]. 北京：中國電力出版社, 2011:17-18.

[2] 水利部農村電氣化研究所.小水電現狀[EB/OL].http:∥www.hrcshp.org/aboutshp/aboutshp.asp?docId=05.2013-12-17.

[3] Cardew-Hall M, Cosmas J, Ristic M. Automated proof inspection of turbine blades[J]. The International Journal of Advanced Manufacturing Technology, 1988,3(2): 67-88.

[4] 金建國, 周明華, 王明怡,等. 曲線參數化模型研究[J]. 浙江大學學報(工學版), 2002,36(1):597-597.

[5] 金建國, 包 曄, 繆永偉. 曲線參數化技術研究與分析[J]. 浙江工業大學學報, 2003,31(5):580-585.

[6] 蔡江畔, 李 春, 李沈堅. 參數曲線在水泵葉輪設計中的應用[J]. 上海理工大學學報, 2008,30(4):311-314.

[7] 張海軍, 郭雪巖, 戴 韌. 飛艇外型設計中曲線參數化方法的比較[J]. 力學季刊, 2012,32(4):634-639.

[8] 曹 鯤, 姚志民. 水輪機原理及水力設計[M]. 清華大學出版社, 1991.

[9] 張禮達, 陳維森. 軸流式轉輪葉片奇點分布法 CAD 軟件設計與研究[J]. 水動力學研究與進展: A 輯, 1998,13(4):397-405.

[10] 薛正福. 風力機適應性葉片的參數化建模與有限元分析[D]. 呼和浩特：內蒙古工業大學, 2009.

[11] 朱國俊, 羅興锜, 郭鵬程, 等. 基于組合優化方法的平面葉柵優化設計[J]. 大電機技術, 2010,(1):50-53.

[12] 崔 濤. 基于遺傳算法的軸流式水輪機葉片優化設計[J]. 現代制造, 2012,(33):122-123.

[13] 嚴 敬, 王 桃, 肖國華, 等. 基于儒可夫斯基變換的軸流葉片翼型設計[J]. 排灌機械工程學報, 2012,30(3):265-269.

[14] 張為民, 郝小忠, 何 磊. 基于 NURBS 的渦輪葉片參數化設計[J]. 機械設計與制造工程, 2013,42(8):23-26.

[15] Floater M S. Analysis of curve reconstruction by meshless parameterization[J]. Numerical Algorithms, 2003,32(1):87-98.

[16] Valakos I M, Ntipteni M S, Nikolos I K. Structural optimization of a centrifugal impeller using differential evolution in CATIATMenvironment[J]. Operational Research, 2007,7(2):185-211.

[17] 閔新勇. 風力機翼型的氣動性能模擬與優化設計[D]. 上海：上海交通大學, 2010.

[18] Liang Y, Cheng X Q, Li Z N, et al. Multi-objective robust airfoil optimization based on non-uniform rational B-spline (NURBS) representation[J]. Science China Technological Sciences, 2010,53(10):2 708-2 717.

[19] Dong Y, Zhang D, Bu K, et al. Geometric parameter-based optimization of the die profile for the investment casting of aerofoil-shaped turbine blades[J]. The International Journal of Advanced Manufacturing Technology, 2011,57(9-12):1 245-1 258.

[20] Heinze K, Schrape S, Voigt M, et al. Probabilistic endurance level analyses of compressor blades[J]. CEAS Aeronautical Journal, 2012,3(1):55-65.

[21] 李文全. 軸流泵葉片動力特性預測模型研究[D]. 西華大學, 2012.

[22] Derksen R W, Rogalsky T. Bezier-PARSEC: An optimized aerofoil parameterization for design[J]. Advances in engineering software, 2010,41(7):923-930.

[23] Allen C B, Rendall T C S. CFD-based optimization of hovering rotors using radial basis functions for shape parameterization and mesh deformation[J]. Optimization and Engineering, 2013,14(1):97-118.

[24] Walton S, Hassan O, Morgan K. Selected engineering applications of gradient free optimisation using cuckoo search and proper orthogonal decomposition[J]. Archives of Computational Methods in Engineering, 2013,20(2):123-154.

[25] Wang Q, Chen J, Pang X, et al. A new direct design method for the medium thickness wind turbine airfoil [J]. Journal of Fluids & Structures, 2013,43(7):287-301.

[26] Mukesh R, Lingadurai K, Selvakumar U. Airfoil shape optimization using non-traditional optimization technique and its validation[J]. Journal of King Saud University-Engineering Sciences, 2014,26(2):191-197.

[27] Vecchia P D, Daniele E, D`Amato E. An airfoil shape optimization technique coupling PARSEC parameterization and evolutionary algorithm [J]. Aerospace Science & Technology, 2013,32(1):103-110.

[28] Pehlivanoglu Y V. Direct and indirect design prediction in genetic algorithm for inverse design problems [J]. Applied Soft Computing, 2014,24:781-793.

[29] Heinze K, Meyer M, Scharfenstein J, et al. A parametric model for probabilistic analysis of turbine blades considering real geometric effects[J]. CEAS Aeronautical Journal, 2014,5(1):41-51.

[30] Murugan S, Woods B K S, Friswell M I. Hierarchical modeling and optimization of camber morphing airfoil [J]. Aerospace Science & Technology, 2015,59(2):31-38.

[31] 李德順, 李仁年, 楊從新,等. 雷諾數對風力機專用翼型氣動性能影響的研究[J]. 流體機械, 2009,37(12):31-34.

[32] Hicks R M, Henne P A. Wing design by numerical optimization[J]. Journal of Aircraft, 1978,15(7):407-412.

[33] Wu H Y, Yang S, Liu F, et al. Comparison of three geometric representations of airfoils for aerodynamic optimization[C]∥16th AIAA Computational Fluid Dynamics Conference. 2003.

[34] 左林玄, 王晉軍. 低雷諾數翼型的優化設計[J]. 兵工學報, 2009,30(8):1 073-1 077.

[35] 尹 強, 高正紅. 外形參數化方法對氣動優化過程的影響[J]. 科學技術與工程, 2012,20(14):3 394-3 398.

[36] 廖炎平, 劉 莉, 龍 騰. 幾種翼型參數化方法研究[J]. 彈箭與制導學報, 2011,31(3):160-164.

[37] Sobieczky H. Parametric airfoils and wings[J].Notes on Numerical Fluid Mechanics,1998:71-88.

[38] 孫 勤, 張俊彥, 鄒汝紅. 三種翼型參數化方法的研究[J]. 湘潭大學自然科學學報, 2013,35(3):34-39.

[39] 劉德民, 程 宦, 袁凌麗. 潮流能水輪機水力特性研究[J]. 東方電機, 2013,41(6):9-12.

[40] 陳紅勛, 霍聰聰, 劉文梅. 基于 CFD 的分段翼型控制研究[J]. 排灌機械工程學報, 2012,30(5):513-516.