基于稀疏表示的電力系統諧波信號頻率分析

張潤涵，扈羅全，2

（1.蘇州大學城市軌道交通學院，江蘇蘇州215131；2.蘇州出入境檢驗檢疫局，江蘇蘇州215104）

?

基于稀疏表示的電力系統諧波信號頻率分析

張潤涵1，扈羅全1，2

（1.蘇州大學城市軌道交通學院，江蘇蘇州215131；2.蘇州出入境檢驗檢疫局，江蘇蘇州215104）

摘要：諧波污染對電力系統和電力設備產生嚴重的危害和影響，當電力信號中存在強大的噪聲成分時，傳統的快速傅里葉變換（fast fourier transform，FFT）無法準確提取出諧波成分。該文在信號稀疏表示理論的基礎上，提出基于稀疏表示的電力系統諧波信號頻率分析方法，并設計出諧波頻率分析快速算法。通過Matlab仿真，結果表明該方法能準確提取諧波成分的頻率，具有較強的抗噪能力。

關鍵詞：諧波分析；頻率分析；稀疏表示；快速傅里葉變換

0　引言

隨著各種非線性負荷特別是電力電子設備在電力系統中的廣泛應用，電力系統的諧波污染日趨嚴重，諧波含量已成為衡量電能質量的重要指標[1]。對電力系統中的諧波頻率成分進行實時測量，確切掌握信號中諧波頻率的實際狀況，對于防止諧波危害，維護電力系統的安全運行具有重要意義。

快速傅里葉變換（fast fourier transform，FFT）因其易于實現而被作為諧波分析的主要方法，已被廣泛應用于電力系統諧波分析領域[2-3]。但FFT算法對噪聲的抗干擾能力弱，當電力信號中存在強大的噪聲成分時，FFT算法無法準確獲取諧波信號的頻率成分。

三角函數基底由不同頻率參量的諧波原子構成，諧波原子與諧波成分匹配度較高，因此諧波信號可由三角函數基底稀疏表示；而噪聲成分與諧波原子匹配度低，因此噪聲信號不能用三角函數基底稀疏表示。基于此，本文引入稀疏表示的思想，提出了一種基于稀疏表示的電力系統諧波信號頻率分析方法。

1　基于稀疏表示的諧波信號頻率分析

1.1諧波信號稀疏表示模型

假設含噪諧波信號的觀測值為

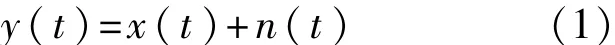
式中，信號x（t）（（M+1）×1維）含有多個諧波成分；n（t）（（M+1）×1維）為噪聲信號。其中x（t）可以表示為

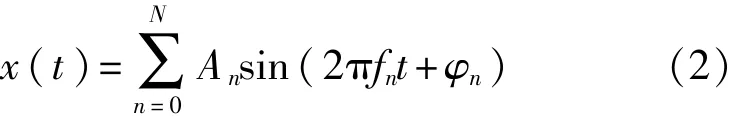
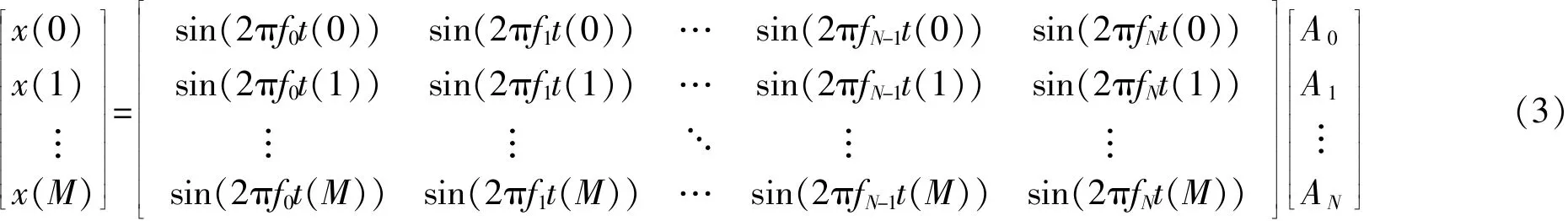
式中：fn——第n次諧波的頻率；

An、φn——第n次諧波的幅值和相位；

N——最高次諧波次數。

諧波恢復的目的就是從含噪信號中估計出真實諧波信號成分。考慮相位φn=0的情形[4-5]，式（2）可以寫成矩陣表示形式：

則真實信號x（t）可以表示成若干個諧波成分的線性疊加和，同時也可以表示成一個三角函數基底與表示系數的乘積。

上述式（3）可看作信號x（t）在三角函數基底上的線性展開，可簡化成：

式中：x——信號x（t）；

S——三角函數基底，為冗余基底；

A——系數。

假設原始信號中只含有p個諧波成分，理論上式（4）中的系數A只含有p個非零值，其余N+1-p個值均為0，是一個稀疏向量，原始信號x（t）可以用該三角函數基底稀疏表示。

1.2三角函數基底稀疏表示快速算法

從觀測信號中估計原始信號x等價于從觀測信號中估計原始信號在三角函數基底上的表示系數A。通常可以利用基追蹤去噪（basis pursuit denoising，BPD）將該稀疏表示問題轉換成線性規劃問題[6]：

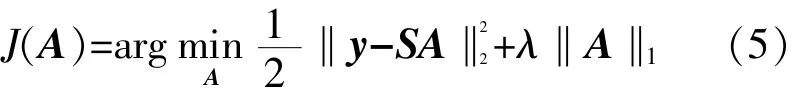
式中λ為拉格朗日乘子。

λ的選取準則可參考文獻[7]。傳統梯度下降法收斂速度慢，Afonso等提出了一種收斂速度更快的優化算法[8]，分裂增廣拉格朗日收縮算法（split augmented lagrangian shrinkage algorithm，SALSA），通過迭代更新表示系數A使得代價函數J（A）最小，最終得到一組最優解，該迭代過程為

1）初始化k，λ，μ，ν0，d0，A0，Nit（迭代次數）。

2）循環開始。

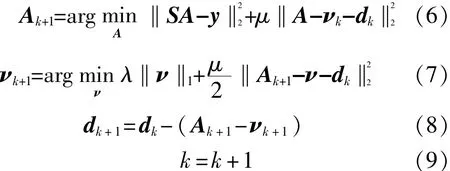
3）當k大于設定迭代次數時（k＞Nit），循環結束。

利用函數求導可以求得二次函數式（6）的解，而式（7）可以利用軟閾值法[9]來求解。決定該算法計算速度的關鍵點在于對基底S的操作是否有快速算法。考慮到基底S的具體形式，在Matlab軟件中設計出基于FFT的快速算法，x=SA和A=S-1x可以利用表1中的函數實現。

通過以上迭代算法可以求得最優解向量A^，則原始信號x的逼近值為x^=SA^。

表1　基于FFT的函數快速求解Matlab代碼

2　仿真算例

為驗證基于稀疏表示的諧波頻率分析方法的有效性，采用類似參考文獻[4-5，10]的仿真算例，對含有多個諧波成分的信號進行仿真分析，該仿真信號為

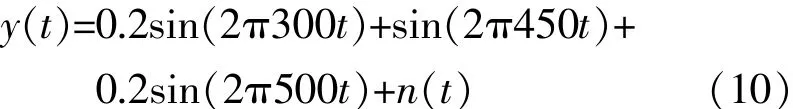
式中n（t）為高斯白噪聲，信號y（t）中含有6次諧波、9次諧波、10次諧波以及噪聲成分。通常用信噪比的大小來描述信號中含噪聲成分的程度，信噪比SNR為

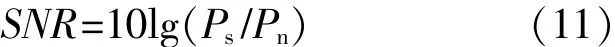
式中：Ps——有用信號的能量；

Pn——噪聲信號的能量。

取噪聲幅值為0.7，使得SNR=0.5411dB，對信號y（t）進行傅里葉分析得其頻譜如圖1所示，表明該信號中含有3個主要諧波頻率成分，分別為f6=300 Hz，f9=450 Hz，f10=500 Hz。但由于噪聲成分的存在，頻譜中存在許多干擾成分。

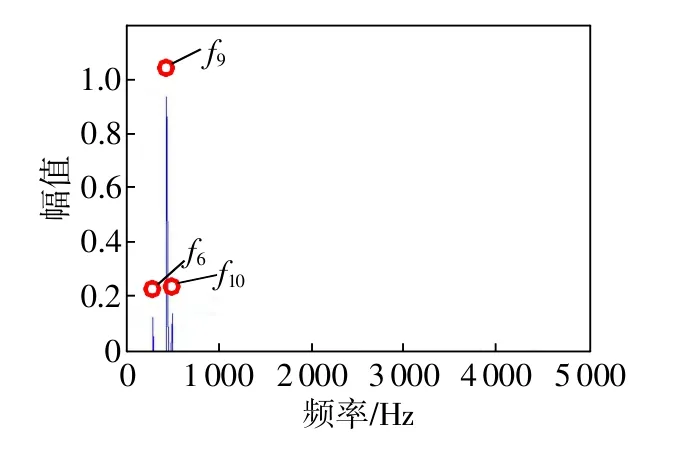
圖1　仿真信號的頻譜圖（SNR=0.5411dB）

利用本文提出的方法分析信號y（t），得其表示系數如圖2所示，可清晰獲取3個諧波頻率成分，分別為f6=300 Hz，f9=450 Hz，f10=500 Hz，信號中的諧波成分與三角函數基底匹配程度高，可以用該基底稀疏表示，而噪聲成分與三角函數基底匹配程度低，不能用該基底稀疏表示。

為進一步驗證該方法對信號中諧波成分提取的有效性和對噪聲的抗干擾能力，針對噪聲幅值為1.4，SNR=-5.4795dB時的含噪諧波信號進行分析。圖3給出了該信號的傅里葉頻譜，圖4給出了該信號的稀疏表示結果。

圖3和圖4表明當噪聲成分比較多時，噪聲對頻譜分析有較大干擾，傅里葉分析難以準確分辨出原始信號中的諧波頻率成分，而本文的方法仍可以稀疏表示原始信號中的諧波頻率成分，具有很好的抗噪能力。

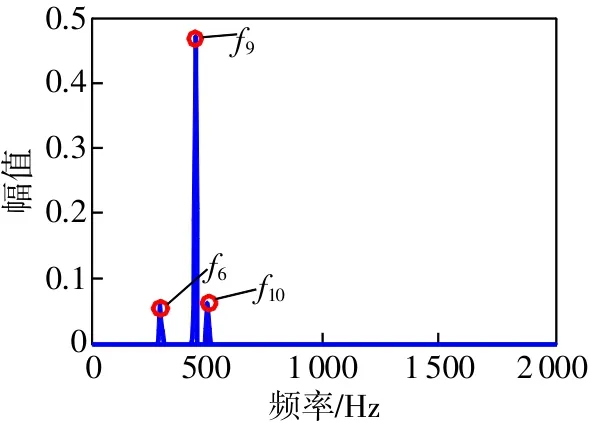
圖2　仿真信號的稀疏表示結果（SNR=0.5411dB）

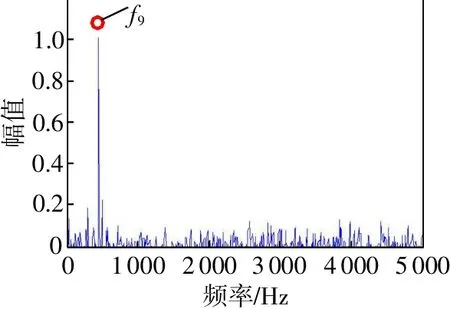
圖3　仿真信號的頻譜圖（SNR=-5.4795dB）

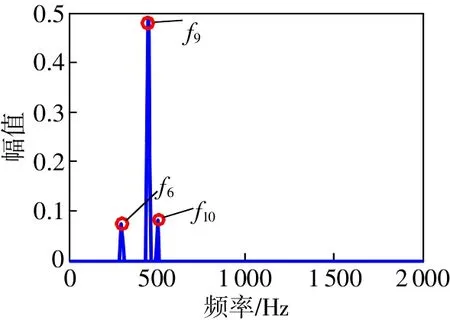
圖4　仿真信號的稀疏表示結果（SNR=-5.4795dB）

3　討論

1）傅里葉頻譜圖可以描繪出原始信號中諧波成分的幅值，而從稀疏表示的結果圖中可以看出，稀疏表示系數的幅值與仿真信號中諧波成分的幅值相差較大，這是由于本文提出的方法是基于基追蹤去噪方法，而基追蹤去噪方法必然會帶來幅值上的衰減。

2）類比傅里葉頻譜圖可以描繪出原始信號中諧波成分的相位，之后的工作將考慮能否利用該稀疏表示方法檢測出諧波成分的相位。

3）本文主要是針對含高斯白噪聲的諧波信號進行分析，之后的工作將包括對含有色噪聲諧波信號進行稀疏表示分析。

4　結束語

本文基于稀疏表示理論提出了一種新的諧波信號頻率分析方法，并設計了基于三角函數基底的Matlab快速算法。仿真結果表明，利用該方法能準確獲取諧波信號的頻率成分，測量準確度高，抗干擾能力強，因此，該算法在電力系統諧波分析中有較高的實用價值。

參考文獻

[1]孟蘋蘋，王洪誠，趙波等.并網變流器三相諧波檢測方法的研究[J].中國測試，2012，38（3）：46-57.

[2]曾博，滕召勝，周毅波.改進FFT非穩態電力諧波分析及應用[J].電工技術學報，2013，27（11）：256-262.

[3]郝珂.電力系統諧波檢測與治理[J].中國測試技術，2006，31（6）：64-67.

[4]沈躍.基于壓縮感知理論的電力系統數據檢測與壓縮方法研究[D].蘇州：江蘇大學，2012.

[5]李天云，程思勇，楊梅.基于希爾伯特-黃變換的電力系統諧波分析[J].中國電機工程學報，2008，28（4）：109-113.

[6] CHEN S S，DONOHO D L，SAUNDERS M A. Atomic decomposition by basis pursuit[J]. SIAM Journal on Scientific computing，1998，20（1）：33-61.

[7] CHEN P Y，SELESNICK I W. Translation-invariant shrinkage/thresholding of group sparse signals [J]. Signal Processing，2014（94）：476-489.

[8] AFONSO M V，BIOUCAS-DIAS J M，FIGUEIREDO M A T. Fast image recovery using variable splitting and constrained optimization[J]. IEEE Transactions on 2010，19（9）：2345-2356.

[9] YU H，WANG G. A soft-threshold filtering approach for reconstruction from a limited number of projections[J]. Physics in Medicine and Biology，2010，55（13）：3905.

[10]李天云，程思勇，楊梅.基于希爾伯特-黃變換的電力系統諧波分析[J].中國電機工程學報，2008，28（4）：109-113.

（編輯：徐柳）

Sparse representation-based analysis of harmonic signal frequency in power system

ZHANG Runhan1，HU Luoquan1，2
（1. School of Urban Rail Transportation，Soochow University，Suzhou 215131，China；2. Suzhou Entry-Exit Inspection and Quarantine Bureau，Suzhou 215104，China）

Abstract:Harmonic waves are harmful to electric power systems and electrical equipment. The analysis of harmonic signal frequency in power system has long been an important subject for electric power designers. Strong background noise in signals will interface harmonic components, thus making them too hard to be derived with the traditional approach -fast fourier transform （FFT）. In this paper, we have designed a fast algorithm for harmonic analysis based on the sparse representation theory. The Matlab -based simulation experiment has shown that the proposed method, because of its strong anti-noise capacity, can be used to extract accurately the frequency of harmonic components.

Keywords:harmonic analysis；frequency analysis；sparse representation；FFT

作者簡介：張潤涵（1990-），男，江蘇鎮江市人，碩士研究生，專業方向為電力系統諧波分析、電能質量檢測與分析。

基金項目：國家質檢總局科研項目（2012IK091）

收稿日期：2015-07-11；收到修改稿日期：2015-08-29

doi：10.11857/j.issn.1674-5124.2016.01.008

文獻標志碼：A

文章編號：1674-5124（2016）01-0035-03