例談中學數學思想與方法的滲透

潘玉琦

?

例談中學數學思想與方法的滲透

潘玉琦

教學案例：比較二次根式的大小。

師：我們知道，兩個正數里，較大的正數的平方也較大，它們的算術平方根是否也具有相同的規律呢？這個問題，大家動手算一算。

學生小組合作，邊計算，邊探討。教師將兩個小組的計算結果用投影儀展示。

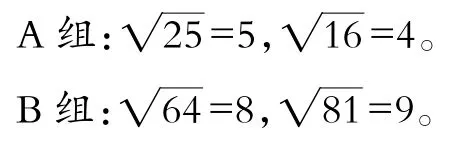
師：請同學們仔細觀察這兩組的結果，你發現了什么？

生1：我發現正數越大，它的算術平方根就越大。

生2：我發現兩個正數的算術平方根進行比較，大數的算術平方根大于小數的算術平方根。

師：這個結論是不是帶有普遍性呢？我們再用幾個其他的數試一試。

學生嘗試歸納，教師總結：一般地，當a＞0，b＞0時，如果a＞b，則有

上述教學案例中，學生通過動手計算，考察了部分正數的算術平方根的大小關系后，用不完全歸納法得出了結論：一般地，當a＞0，b＞0時，如果a＞b，則有

正如案例中所體現的一樣，數學思想與方法往往隱含在知識里，體現在知識的發生、發展過程。實踐證明，在課堂中滲透數學思想與方法，能使學生快速掌握知識的內涵，提高學生的數學素養。那么如何滲透呢？

在知識的發生過程中滲透。數學教學內容從總體上可分為兩個層次：一個稱為表層知識，包含概念、性質、法則、公式、公理、定理等基本內容；另一個稱為深層知識，主要指數學思想與方法。表層知識是深層知識的基礎，具有較強的操作性。學生只有通過對教材的學習，在掌握與理解一定的表層知識后，才能進一步學習和領悟相關的深層知識。而數學思想與方法又是以數學知識為載體，蘊含于表層知識之中，是數學的精髓，支撐和統率著表層知識。教師在講授概念、性質、公式的過程中，應不斷滲透相關的數學思想與方法，讓學生在掌握表層知識的同時領悟到深層知識，從而使學生的思維產生質的飛躍。只講概念、定理、公式而不注重滲透數學思想與方法的教學，將不利于學生對所學知識的真正理解和掌握，使學生的知識水平永遠停留在初級階段，難以提高。在教學過程中，教師可以引導學生主動參與結論的探索、發現、推導過程，搞清其中的因果關系，領悟它與其他知識的關系，讓學生親身體驗創造性思維活動中所經歷和應用到的數學思想與方法。

在問題的探索、解決過程中揭示。我們的教學一直存在這么一個現象：題目講得不少，可只要條件稍作改變，一些學生就會不知所措，總是停留在模仿型解題的水平上，很難形成較強的解決問題的能力，更談不上創新能力的形成。這主要是由于教師沒有將題目所蘊含的數學思想與方法予以揭示。在教學解決問題的過程中，教師應把最多的精力花在誘導學生怎樣去想，怎樣想到，到哪里去找解題的思路上，要將數學思想與方法的運用置于解題教學的中心位置，充分發揮數學思想與方法的解題功能——定向功能、聯想功能、構造功能和模糊延伸功能。若學生能在解決問題的過程中充分發揮數學思想與方法的解題功能，不僅可少走彎路，還可大大提高數學能力與綜合素質。

（作者單位：安徽省滁州市第八中學）

探索