改編例題　精彩不斷

楊昌義

?

改編例題精彩不斷

楊昌義

湘教版數學教材七年級下冊中安排了這樣一道例題：如圖1，AB椅DC，蟻BAD= 蟻BCD，那么AD椅BC嗎？學生由于剛剛才學平行線的性質和判定定理，對公理化證明方式還只是初步接觸。可能為了減少難度，教材事先已連好了對角線AC，把思維直接固定在用“內錯角相等，兩直線平行”這一條思路上，但這樣不利于學生發散思維的培養。為此，筆者上課時去掉了對角線AC，讓學生自由發揮。下面再現課堂情景。

上課伊始，教師出示題目：如圖2，AB椅DC，蟻BAD=蟻BCD，那么AD椅BC嗎？隨即引導學生思考——

師：同學們，我們已學了3種平行線的判定方法，分別是哪3種？

生：方法1，同位角相等，兩直線平行；方法2，內錯角相等，兩直線平行；方法3，同旁內角互補，兩直線平行。

師：答得非常好！那么，你們怎么應用這些方法判定題目中的AD椅BC呢？

生：圖中沒有同位角，也沒有內錯角，顯然，方法1、2都不能用，看來只有用方法3了。

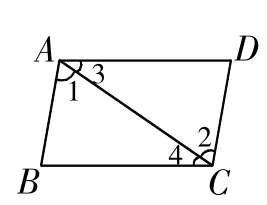
圖1

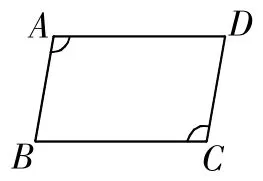
圖2

師：分析得有道理。但用方法3，必須找到相對應的同旁內角。與AD椅BC相對應的同旁內角有哪些？

生1：與AD椅BC相對應的同旁內角是蟻ABC與蟻BAD，因為它們是直線AD、BC被直線AB所截出來的。

生2：還有蟻BCD和蟻ADC，但只要推出一對角相等就行了。

師：不錯！結合已知條件，能推出嗎？

生3：由AB椅CD可得蟻ABC+蟻BCD=180毅，兩直線平行，同旁內角互補。

師：這兩個角互補又有什么用？

生4：有用！因為已知蟻BAD=蟻BCD，由等量代換得蟻ABC+蟻BAD=180毅，于是，由方法3可得AD椅BC，很簡單！

師：數學就是很奇妙，你如果知道結論了，就會覺得很簡單。而開始不知道的時候，卻吸引你去苦苦探究。一旦突破了，心里會有一種特別的舒暢和愉快感，讓人回味無窮，這就是數學的魅力！

生5：幾何比代數有趣多了！

師：其實數學都有趣，無論是代數還是幾何，只要我們進了它的門檻，就是邁進了瑰麗的“萬花筒”，里面精彩不斷，奧妙無窮！比如，對于上面這題，只要發揮我們的聰明智慧，還是可以應用方法1、2解答的！

生6：不是沒有內錯角、同位角嗎？

師：我們可以想辦法構造出來。可以連結BD，內錯角是不是就有了？

生6：可以這么做嗎？

師：完全可以！為了做題的需要，有時需要作一些線，這種補作的線叫做“輔助線”，一般用虛線畫，它能輔助我們完成做題任務。例如，作出輔助線BD（如圖3），我們馬上得到了內錯角，同學們能找出幾對？生（齊）：兩對：蟻ADB和蟻CBD，蟻ABD和蟻CDB。師：與將要證明的AD椅BC有關的是哪一對？為什么？

生7：蟻ADB和蟻CBD。因為它們是直線AD、BC被直線DB所截出來的。

師：回答得非常正確！只要它們相等，由方法2就可以立即得到AD椅BC。那么我們怎么通過條件得到蟻ADB=蟻CBD呢？

生8：由已知AB椅CD，得到蟻ABD=蟻CDB。已知蟻ABC=蟻ADC，由等式的性質得蟻ABC原蟻ABD= 蟻ADC原蟻CDB，于是可得蟻CBD=蟻ADB。

師：你簡直太有才了！

生8：這歸功于輔助線，非常有用！但我不知道什么時候要作輔助線，也不知怎么作。

師：當題目條件不夠時，可以考慮作輔助線，一般有規律可循。有時一道題作的輔助線并不是固定一種，只要對做題有用，都是可以靈活作出的。

生9：那么此題我不連結BD，連結AC（如圖4）行嗎？

師：你們想想看，行嗎？

生10：當然行，只要能得出蟻DAC=蟻ACB。

師：有道理！已知蟻ABC=蟻ADC，那么蟻BAC= 蟻ACD嗎？

生11：相等！因為已知AB椅CD，兩直線平行，內錯角相等。

師：在吟ABC和吟ADC中，已有兩對內角相等了，第三對角難道不等嗎？

生12：相等！三角形內角和是180毅，小學已學了。

師：現在問題不是也解決了？

生13：輔助線真妙啊！

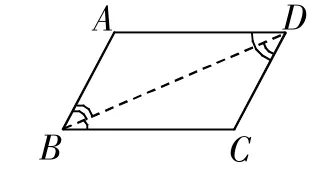
圖3

圖4

師：更妙的還在后面呢！如果我們再仔細思考，這道題還能用方法1解答呢！生14：還能用方法1？同位角沒有，怎么做呢？師：為什么不請輔助線幫忙呢？比如，延長BC……

生14：也可以這么作嗎？

師：可以！只要對我們有用，怎么作都行！大家想想，延長BC 至E（如圖5），有用嗎？

生15：有用！只要我們能夠證明蟻ADC=蟻DCE即可。

師：請大家探究：蟻ADC=蟻DCE嗎？

生16：已知蟻ADC=蟻ABC，只要得出蟻ABC= 蟻DCE，用等量代換即可。

生17：蟻ABC=蟻DCE，這是明擺著的，因為已知AB椅CD，同位角相等的呀！

師：不是又成功了嗎？生18：真是妙不可言！師：大家再想想，我們是否還能在不同位置、不同方向作輔助線呢？

生：老師，我們作出來了，不知行不行，請您檢查下（如圖6所示）。

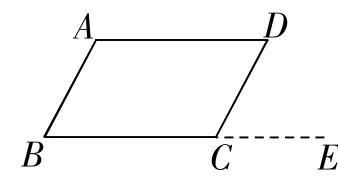
圖5

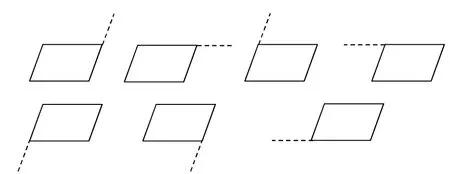
圖6

師：太棒了！真是精彩紛呈，美不勝收啊！告訴大家，這些作法都行！像剛才探究的一樣，能不能化成用方法1解答？課后同學們可以試試。

教學后記：一題多解對于訓練學生的發散思維，培養學生的創新意識十分有益。在本案例中，教師首先讓學生明確判定兩直線平行的基本方法，然后圍繞問題的結論，引導、啟發學生如何選擇方法，師生共同歷經了探究的全過程。師生不斷地互提問題，并通過提問使探究活動步步推進、環環相扣。尤其是教師不失時機地介紹了添作輔助線的方法，讓學生感受到輔助線在說理中的巧妙作用，激發了學生的興趣和潛在的創新精神。這樣教學，不僅讓學生順利地解答出問題，還滲透了化歸思想和“執果索因”的說理方法，也培養了學生的發散思維和演繹推理能力。

（作者單位：永州市零陵區永州柳子中學）

探索