一種固定基線單頻整周模糊度求解方法

張　偉，高　珊

(1.深圳市大疆創新科技有限公司，廣東　深圳　518057；2.廣州海格通信集團股份有限公司，廣州　510663)

?

一種固定基線單頻整周模糊度求解方法

張偉1，高珊2

(1.深圳市大疆創新科技有限公司，廣東深圳518057；2.廣州海格通信集團股份有限公司，廣州510663)

摘要：針對最小二乘方法求解單頻多歷元數據模糊度浮點解時需進行高階矩陣運算，導致運算量過大的問題，提出了一種結合序貫平差和最小二乘模糊度去相關調整方法求解固定基線單頻整周模糊度的算法。文中分別闡述序貫平差算法和最小二乘模糊度去相關調整方法的原理，以及序貫平差求解模糊度浮點解和協方差陣、最小二乘模糊度去相關調整方法搜索整數解的過程，最后通過殘差比值和先驗信息固定正確的模糊度。結果表明本方法計算量小，可以在實時嵌入式平臺中運行，用低成本實現GPS高精度應用。

關鍵詞：單頻整周模糊度；最小二乘模糊度去相關調整方法；序貫平差；固定基線

0引言

全球定位系統(global positioning system，GPS)載波差分定位已經在全球得到了廣泛應用，包括測量測繪、地表檢測、精準農業、無人機、飛機精密進近等多個行業和領域。目前載波差分定位主要采用雙頻接收機實現，較少使用單頻。

載波差分定位算法核心是解算整周模糊度，研究人員提出了許多方法，包括模糊度映射函數(ambiguity function method，AFM)技術[1]、最小二乘搜索(least squares search，LSS)技術[2-3]、快速模糊度解算方法(fast ambiguity resolution approach，FARA)[4]、快速模糊度搜索濾波器(fast ambiguity search filter，FASF)方法[5]、最小二乘模糊度去相關調整方法(least ambiguity decorrelation adjust，LAMBDA)[6]等，這些方法大多針對雙頻觀測量提出。雙頻組合觀測量波長比單頻長，模糊度搜索范圍小。但雙頻接收機價格比單頻接收機高，如何利用低成本單頻接收機實現載波差分定位是目前的一個研究熱點。

單頻載波差分定位的關鍵在于整周模糊度的解算，同樣可以使用LAMBDA方法，一般需要多個歷元數據才能求解。在處理多歷元數據時，傳統方法是用采用最小二乘計算浮點解，求解過程中存在高階矩陣相乘和求逆，只能通過計算機進行事后處理，無法在嵌入式平臺中實時計算，限制了單頻載波差分的應用。本文采用序貫平差方法計算浮點解，對各歷元數據進行間接平差處理，解決了高階矩陣運算的問題。LAMBDA搜索整周模糊度解后，同時采用比值檢驗和先驗信息對整周模糊度進行確認并固定模糊度。通過仿真實驗對算法進行驗證，證明算法可在嵌入式平臺中進行實時計算，對于固定基線模糊度求解具有良好效果。

1整數最小二乘問題

載波差分定位的雙差觀測方程為[7]

y=Bb+Aa+e

(1)

式(1)中，y為m×1階雙差載波相位觀測量，b為p×1階基線矢量，a為n×1階雙差模糊度且為整數(a∈Zn)，B為基線矢量的m×p階設計矩陣，A為模糊度的m×n階設計矩陣，e為觀測噪聲。固定基線時基線矢量保持不變，此時p=3。方程中的基線矢量和雙差模糊度為待定參數。

式(1)的解算步驟分為3步[8-10]：

2)搜索模糊度整數解，按照一定的判決準則獲取最優解；

3)模糊度整數解固定后求解基線矢量。

模糊度整數解的估計準則為[11]：

(2)

式(2)為整數的最小二乘非標準誤差模型，整數模糊度解法稱之為整數最小二乘方法，整數搜索算法是其中的關鍵。

2模糊度浮點解計算

假設每個歷元的觀測衛星保持不變，共計n+1顆衛星，構造n個雙差模糊度。對于單歷元而言，共計n個方程，待定參數n+3， 顯然單歷元無法解出待定參數，需要采用多歷元解算。多歷元數據的浮點解可以用最小二乘或序貫平差求解，兩者的計算量存在差異。以下將闡述兩種算法的原理和計算過程，并分析兩者的計算量。

2.1浮點解計算過程

對于固定基線的多歷元載波雙差方程，假定衛星保持不變，待定參數為n+3。 歷元數為g，A矩陣和B矩陣的行數m=g×n， m≥n時式(1)為滿秩最小二乘問題，可用標準方程求解。標準方程為

(3)

本文采用序貫平差的方法來解決這個問題，將觀測量歷元分成多組，按順序分別做相關間接平差，達到整體平差的效果，計算量分散在各個歷元。具體方法為

1)選取兩個歷元的觀測量計算初始解，此時有2n個方程，只需滿足2n≥n+3， 即n≥3， 按式(3)就可以計算出浮點解和協方差，實際應用中一般要求n≥5；

2)計算出初始解后，每獲取一組新的歷元觀測數據，采用序貫平差的方式更新浮點解和協方差陣。

浮點解和協方差陣的更新依據序貫平差的原理進行，具體為[12]

(4)

(5)

按間接平差濾波原理得到的遞推解為

(6)

式(6)中，

(7)

(8)

(9)

引入符號

(10)

則遞推結果整體表示為

(11)

誤差估計為

(12)

式(11)中，各矩陣行數和列數的最大值均為n+3。在計算初始解之后，每個歷元按照式(11)更新浮點解和協方差陣，計算量保持不變，嵌入式系統可負荷。浮點解和協方差陣計算之后，每個歷元再用LAMBDA方法求解模糊度整數解。

2.2計算量分析

為簡化分析，最小二乘和序貫平差中的權陣取單位陣，乘法運算時其計算量不予考慮。

(13)

根據矩陣相乘的運算量計算方法，式(3)的浮點加法和乘法運算次數均為g×(n3+7n2+12n)+(n+3)2。 式(3)還包括一次對n+3階矩陣求逆的運算。

用相同方法分析序貫平差的運算量，g=2時序貫平差和最小二乘計算量相等。g>2時浮點加法運算次數為6n3+36n2+66n+34， 浮點乘法運算次數為6n3+36n2+62n+27。 序貫平差計算過程中還包括一次n階矩陣求逆的運算。

由以上分析可知，當變量保持不變時，傳統最小二乘的運算量和歷元數成正比，而序貫平差的運算量保持不變，當歷元數大于5時，序貫平差的運算量開始小于最小二乘。

3LAMBDA方法求解整數解

模糊度的整數解按照估計準則式(2)來進行搜索，即求χ2(α)的最小值。需要在離散空間中模糊度計算χ2(α)求取最小值，沒有標準解法。首先需要將整數解空間Zn縮小到一個子空間，且該子空間包含整數解。該子空間可以表示為[13]

(14)

3.1基本原理

LAMBDA算法基本原理為[13-14]：

1)a∈Zn， 尋找n×n階矩陣Z， 滿足：a為整數時，z=ZTa也為整數；z為整數時，a=(ZT)-1z也為整數。此條件等價于[8]：Z中所有元素為整數，且det(Z)=±1；

2)對原始矩陣做如下變換：

(15)

(16)

搜索空間變換為

(17)

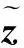
3.2搜索空間的確定

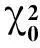
4整周模糊度確認

整周模糊度求解的最后一個步驟是模糊度確認，主要功能是從可能的整周模糊度整數解中選取最優解，并驗證其正確性。如果固定的模糊度錯誤，基線解將一直錯誤。

最常用的一種檢驗方法是比例檢驗法[14]，通過次小殘差平方和與最小殘差平方和的比值來檢驗，即

(18)

式(15)中，Ω2為次小殘差平方和，Ω1為最小殘差平方和，τ為閾值。ratio大于τ認為最優解正確。

τ的取值很關鍵，文獻[15]建議取2，但在實際應用中太小，應按照實際情況進行取值。

單頻載波差分定位用幾個歷元來確定整周模糊度較難實現，正確的模糊度應具有重復性，因此可以通過多歷元驗證模糊度的正確性，即序列有效性檢驗。由于采用序貫平差算法，隨著歷元數的增多，理論上系統噪聲會降低，因此正確模糊度的ratio值從整體上而言隨著歷元的增多而增大。如果連續一段時間內，搜索到的最優模糊度相同，ratio值均大于閾值，且整體上隨著歷元數的增多而增大，即可以認為該組模糊度是正確的模糊度解。

基線矢量的先驗信息也可用于模糊度檢驗。在短距離定向時，可以知道基線長度的大概范圍。正確的模糊度解對應的基線長度需要滿足該范圍，不滿足則認為不是正確解[16]。

如果能獲取偽距觀測量，可以進行偽距差分定位。偽距差分定位結果的誤差一般在4 m內，可以用偽距差分計算的基線矢量同載波差分計算的基線矢量比較，兩者的誤差超過一定范圍則認為該整數解錯誤。

5仿真實驗

通過三組實驗來驗證算法正確性和算法性能，包括4 m短基線定向實驗、500 m基線靜態實時差分定位(real-time kinematic，RTK)解算實驗以及3 000 m基線靜態RTK實驗。

定向實驗設備為定位定向接收機，可采集GPS L1頻點數據，運行平臺為數字信號處理器(digital signal processor，DSP)。接收機的兩個天線固定放置，距離約4 m，接收機輸出L1頻點觀測數據和基線解算結果，數據頻度為1 Hz。接收機5 min內定向成功則復位，未成功等待定向成功后復位。復位次數共計1 436次，輸出基線矢量結果的歷元數共計267 907組。

采用天寶公司GPS數據后處理軟件解算觀測數據，得到基線長度為4.056 m，基線矢量為(-3.105 m，-2.077 m，1.579 m)，方位角為64.974°。和后處理軟件計算結果比較，定位定向接收機計算的直角坐標系下軸向誤差均在0.02 m內，基線長度誤差在0.01 m內，方位角誤差在0.1°以內。誤差曲線如圖1所示。

圖1　短基線定向基線矢量誤差

1 436組觀測數據均計算出正確的整周模糊度，從可以進入模糊度解算的歷元開始算起，最長的模糊度固定時間為470 s。整周模糊度固定時間的統計如表1所示。

表1　4 m基線模糊度固定時間統計

RTK實驗是在某樓頂架設基準站，基準站信息和觀測數據通過電臺發射。基準站接收的頻點包括GPS L1/L2。流動站的電臺接收到基準站數據后發送給GPS L1/L2雙頻接收機。接收機觀測數據和基準站數據采集后進行后處理仿真。首先采集1 h的GPS雙頻數據供天寶后處理軟件解算基線矢量，1 h之后流動站接收機每采集6 min數據后復位一次。由于時間所限，500 m基線實驗共復位61次，3 000 m基線共復位58次。

500 m基線天寶后處理軟件解算得到基線長度為498.086 m，基線矢量為(-61.409 m，-249.464 m，426.716 m)。和天寶后處理結果比較，本文算法的軸向誤差在0.03 m內，基線長度誤差在0.03 m內。誤差曲線如圖2所示。

圖2　500 m基線誤差

500 m基線整周模糊度固定時間的統計如表2所示。

表2　500 m基線模糊度固定時間統計

3 000 m基線天寶后處理軟件解算得到基線長度為2 945.623 m，基線矢量為(1 831.651 m，1 554.291 m，-1 704.679 m)。和天寶后處理結果比較，本文算法的軸向誤差在0.05 m內，基線長度誤差在0.05 m內。誤差曲線如圖3所示。

圖3　3 000 m基線誤差

3 000 m基線整周模糊度固定時間的統計如表3所示。

表3　3 000 m基線模糊度固定時間統計

對三組試驗的原始觀測值進行后處理仿真，比較序貫平差和標準最小二乘解算浮點解的運算時間，對比結果如表4。

表4　序貫平差和最小二乘解算浮點解時間比較

從實驗結果可知，序貫平差計算浮點解的計算量較穩定，歷元數5個以上時，最小二乘的計算量超過序貫平差，且計算量和歷元數呈正比。模糊度固定時間和基線長度呈正比，主要原因是距離增加導致兩點之間信號傳播空間誤差的相關性降低，需要更長的時間進行固定。基線解算誤差和基線距離呈正比，原因可能是天寶后處理軟件采用雙頻去電離層組合求解基線，而單頻差分無法完全消除電離層誤差，導致誤差增大。

6結束語

單頻載波差分定位具有成本低，系統組建簡便的特點，在某些領域具有較高的應用價值。本文采用序貫平差方法計算整周模糊度浮點解，LAMBDA方法求解整周模糊度整數解，并利用ratio方法和基線矢量的先驗信息對模糊度進行固定，實驗結果表明該方法可行。該方法具有求解速度快、計算量小、適用于實時嵌入式系統等特點，可應用于靜態定向和靜態RTK等領域。

參考文獻

[1]MADER G L.Rapid static and kinematic global positioning system solutions using the ambiguity function technique[J].Journal of Geophysical Research，1992，97(B3)：3271-3283.DOI：10.1029/91JB02845.

[2]HATCH R.Instantaneous ambiguity resolution[C]//The Institute of Navigation.Kinematic Systems in Geodesy，Surveying，and Remote Sensing.New York：Springer，1991(4)：299-308.DOI：10.1007/978-1-4612-3102-8_27.

[3]HATCH R.Ambiguity resolution in the fast lane[C]//The Institute of Navigation.Proceedings of the 2nd International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS 1989).Colorado Springs，CO：The Institute of Navigation，Inc.，1989：45-50.

[4]FREI E，BEUTLER G.Rapid static positioning based on the fast ambiguity resolution approach FARA：theory and first results[J].Manuscripta Geodaetica，1990，15(6)：1059-1067.

[5]CHEN Dingsheng.Fast ambiguity search filter (FASF)：a novel concept for GPS ambiguity resolution[C]//The Institute of Navigation.Proceedings of the 6th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS 1993).Salt Lake City，UT：The Institute of Navigation，Inc.，1993：781-787.

[6]TEUNISSEN P J G.Least-squares estimation of the integer GPS ambiguities[R].Beijing，International Association of Geodesy，1993.

[7]TEUNISSEN P J G.The Least-squares ambiguity decorrelation adjustment：a method for fast GPS integer ambiguity estimation[J].Journal of Geodesy，1995，70(1)：65-82.DIO：10.1007/BF00863419.

[8]TEUNISSEN P J G.A new method for fast carrier phase ambiguity estimation[C]//The Institute of Electrical and Electronics Engineers(IEEE).Proceedings IEEE Position，Location and Navigation Symposium PLANS94.Las Vegas，NV：IEEE，1994：562-573.DOI：10.1109/PLANS.1994.303362.

[9]JONGE P J DE，TIBERIUS C C J M.A new GPS ambiguity estimation method based on integer least squares[C]//The Institute of Navigation.Proceedings of the 3rd International Symposium on Differential Satellite Navigation Systems DSNS94.London：The Institute of Navigation，Inc.，1994：9.

[10]JONGE P J DE，TIBERIUS C C J M.Fast positioning using LAMBDA method[C]//The Institute of Navigation.Proceedings of the 4th International Symposium on Differential Satellite Navigation Systems DSNS95.Bergen：The Institute of Navigation，Inc.，1995：8.

[11]JONGE P J DE，TIBERIUS C C J M.The LAMBDA method for integer ambiguity estimation：implementation aspects，Delft Geodetic Computing Centre LGR Series，No.12[R].Delft,The Netherlands:Delft University of Technology，1996.

[12]宋力杰.測量平差程序設計[M].北京：國防工業出版社，2008：89-93.

[13]TEUNISSEN P J G，TIBERIUS C C J M.Integer least-squares estimation of the GPS phase ambiguities[C]//International Association of Geodesy.Proceedings of International Symposium on Kinematic Systems in Geodesy，Geomatics and Navigation KIS94.Banff，Canada：International Association of Geodesy，1994：221-231.

[14]TEUNISSEN P J G.The invertible GPS ambiguity transformations[J].Manuscripta Geodaetica，1995，20(6)：489-497.

[15]LANDAU H，EULER H.On the fly ambiguity resolution for precise differential positioning[C]//The Institute of Navigation.Proceedings of the Fifth International Technical Meeting of the Institute of Navigation，Albuquerque：The Institute of Navigation，Inc.，1992：607-613.

[15]徐金玉，吳簡彤，應畑標.動態快速求解整周模糊度的LAMBDA算法[C]//中國造船工程學會.2006年船舶通訊導航學術會議論文集.上海：中國造船工程學會，2006：188-191.

A Single Frequency Ambiguity Calculation Algorithm in Fixed Baseline

ZHANGWei1，GAOShan2

(1.DaJiang Innovation Technology Co.，Ltd.，Shenzhen 518057，China；2.Guangzhou Haige Communications Group Incorporated Company，Guangzhou 510663，China)

Abstract：Generally，the fixed baseline’s single frequency integer ambiguity resolution calculated by multiple epoch data，the first step is to calculate the ambiguity float solution-traditionally use least squares method.When dealing with multiple epoch data，this method requires high-order matrix operations，leading to excessive computation.Aiming this problem，the paper proposes a new algorithm of fixed baseline single frequency multi-epoch ambiguities resolution that be combined with sequential adjustment and the LAMBDA method.Each epoch data indirect adjust by sequential adjustment algorithm in sequence.Therewith，the float ambiguities and their variance covariance matrix computed.The LAMBDA method provides the integer least-squares estimate for the ambiguities.In the last，using ratio method and auxiliary information fix the precise integer ambiguities.The result indicate this method is a small amount of calculation and can run in real time embedded platform，and with low cost to achieve high precision GPS application.

Key words：single frequency integer ambiguity；LAMBDA；sequential adjustment；fixed baseline

中圖分類號：P228

文獻標識碼：A

文章編號：2095-4999(2016)-01-0088-06

作者簡介：第一張偉(1983—)，男，江西贛州人，工程師，主要從事衛星導航高精度定位研究。

收稿日期：2015-06-01

引文格式：張偉，高珊.一種固定基線單頻整周模糊度求解方法[J].導航定位學報，2016，4(1)：88-93.(ZHANG Wei，GAO Shan.A Single Frequency Ambiguity Calculation Algorithm in Fixed Baseline[J].Journal of Navigation and Positioning，2016，4(1)：88-93.)DOI：10.16547/j.cnki.10-1096.20160117.