中小企業信用再擔保體系演化穩定條件分析

汪 輝，鄧曉梅，楊偉華，馮 珂

(1.清華大學建設管理系，北京 100084；2.軍事經濟學院軍隊財務系，湖北 武漢 430035)

中小企業信用再擔保體系演化穩定條件分析

汪 輝1，2，鄧曉梅1，楊偉華2，馮 珂1

(1.清華大學建設管理系，北京 100084；2.軍事經濟學院軍隊財務系，湖北 武漢 430035)

為研究非強制性再保情況下，中小企業信用再擔保體系穩定發展應具備的條件，本文建立中小企業信用擔保與再擔保機構行為策略的演化博弈模型，利用微分方程穩定性原理求解演化穩定策略，并確定再擔保體系穩定發展所需的條件；以此為基礎，在保證再擔保體系穩定發展的前提下，定量描述了擔保和再擔保機構之間的風險分擔比例、再擔保保費、最低政府風險補貼要求等再擔保運營機制具有的可調節范圍；最后，結合算例進行驗證和應用分析。研究發現：1)若擔保機構加入再擔保體系后，同時滿足再擔保機構增加的收益為正、擔保機構增加的收益大于申請成本，則可保證再擔保體系穩定發展；2)代償率對再擔保運營機制的可調節范圍有重要影響，代償率越高，風險分擔比例、再擔保保費具有的可調節空間越小，若隨代償率上升不存在調節空間時，需要政府對擔保、再擔保機構進行適當的風險補貼，以保證再擔保體系穩定發展。這些研究結果為我國中小企業信用再擔保的實踐提供了理論參考。

中小企業信用再擔保；演化穩定條件；可調節范圍

1 引言

中小企業信用再擔保是中小企業信用擔保體系的拓展和延伸，指以國家政策為導向，通過再擔保合約，由再擔保機構為中小企業信用擔保(以下簡稱“擔保”)機構提供一定比例的再擔保責任，實現為擔保機構增信和分散風險的一種制度安排[1-4]。不同于一般的信用再擔保，中小企業信用再擔保(以下簡稱“再擔保”)不以盈利為目的，通常可獲得政策扶持，如財政資金支持、稅收優惠、貼息貸款等，同時擔保、再擔保保費確定也要體現政策特點。

目前，具有穩定中小企業信用再擔保體系的國家主要有日本、韓國、德國等。在這些國家，依據相關法律，擔保機構將被自動納入再擔保體系，每筆擔保業務實行自動再擔保[5]。結合我國的特點，中小企業信用再擔保體系建設應堅持“政策性引導、公司化管理、市場化運作”的模式[2-4]，并未將擔保機構自動納入再擔保體系，這意味著再擔保機構需要通過市場機制建立與擔保機構之間的再擔保關系。在非強制性自動再保的市場條件下，擔保和再擔保機構是直接的被擔保人和擔保人，他們的行為策略對再擔保體系的穩定發展有著重要的直接影響。那么，通過市場化手段吸引擔保機構選擇加入再擔保體系，進而形成穩定的再擔保體系應具備什么條件？在保證再擔保體系穩定發展的前提下，擔保與再擔保機構之間的風險分擔、再擔保保費具有多大的可調整空間？最低政府補貼應滿足什么要求？這些都是當前我國再擔保體系發展中迫切需要解決的問題。

目前，國外學者主要圍繞中小企業信用擔保展開研究，內容涉及面廣，如擔保資金壓力測試[6]、擔保體系內中小企業違約概率預測[7]、擔保保費估計[8]、擔保政策效果評估[9]等等，但較少涉及再擔保的內容。國內關于再擔保的文獻除再擔保模式方面的研究外，主要聚焦于以下三個方面。一是關于再擔保體系中風險分擔和再擔保保費問題的研究：于孝建和徐維軍[10]采用數理模型分析方法，通過分析各合作方的風險和收益，確定最優風險分擔比例；薛鈺顯和王東超[11]利用討價還價博弈模型分析了擔保、再擔保機構之間風險比例確定的方法，認為風險分擔比例應由擔保、再擔保機構的消耗系數及保費確定。二是關于政府補貼問題的研究：林平和袁中紅[12]通過對廣東省信用擔保機構的全面考察，建議應建立基于再擔保的風險補償機制和財政彌補機制；蔡文宇和陳玉菁[13]通過靜態博弈分析，認為中小企業信用擔保體系引入政府補貼有助于增強擔保市場的有效需求和供給；財科所[14]分析了財政支持中小企業信用擔保的必要性、可行性，在借鑒國外成功經驗做法基礎上，針對我國當前擔保體系中存在的問題，提出應該建立財政資金支持擔保體系的長效機制、促進財政支持路徑的集中化和系統化；馮濤等[15]通過建立數理模型對不同的財政資助方式進行比較分析，認為通過再擔保機構對擔保體系進行風險補貼是最優選擇。三是關于再擔保體系中各方經濟效益的研究：如馬國建等[16]、梅強等[17]利用仿真手段研究了再擔保體系中各方的經濟效益。

這些成果為再擔保實踐起到了一定的指導作用，但都以完全理性人假設為基礎，與現實存在一定差距；也未考慮再擔保體系發展的穩定性問題，更未涉及在確保再擔保體系穩定發展的前提下，不同再擔保運營機制所具有的動態調節空間。

實際上，在非強制性自動再保的市場條件下，再擔保系統的發展過程是擔保與再擔保機構之間不斷博弈的過程，由于未來的不確定性，不可能通過一次博弈就達到均衡狀態，需要從動態的角度，探尋雙方博弈行為策略的調整過程、演化趨勢和穩定性條件。因此，面對未來的不確定性，參與博弈的擔保、再擔保機構更符合有限理性的假設，可自由確定自身的行為策略，通過不斷地模仿學習，從各自的策略集合中選擇較優策略，以提高環境適應能力。

演化博弈理論是從系統論出發，以有限理性為基礎，通過“復制動態”、“最優反應動態”等學習調整機制描述群體模仿學習、調整策略的演化博弈過程[18]。其中，復制動態適合描述大群體、學習速度較慢的演化博弈過程，即，每種策略在當前階段的收益將決定下一階段采取該策略的參與者數量在群體中所占的比例，經過長期的重復，采取較高收益策略的參與者數量在群體中的比例將會越來越高，而采取較低收益策略的群體比例會越來越低，直至最后消亡[19]。與傳統博弈理論相比，演化博弈以有限理性假設為前提，更加貼近現實，在經濟、社會、環境等相關領域得到了廣泛應用[20-22]。

因此，在再擔保系統中，將具有一定數量的擔保和再擔保機構看成兩個不同的群體，由于這兩類群體都是集體決策，不同機構之間存在信息不對稱，他們從認知不足到策略調整的反饋過程較慢，利用復制動態來研究他們策略選擇的互動機制，探索形成穩定再擔保體系所應滿足的條件，將更加貼近實際。

與已有研究不同，本文將運用演化博弈理論，假設擔保、再擔保機構屬于有限理性人，構建擔保和再擔保機構的行為策略演化博弈模型；然后利用微分方程穩定性原理尋找系統的演化穩定策略(ESS，Evolutionary Stable Strategy)及其條件，進而確定通過市場化手段形成穩定再擔保體系應具備的條件；在保證再擔保體系穩定發展的前提下，進一步分析擔保與再擔保機構之間的風險分擔、再擔保保費以及最低政府補貼要求等再擔保運營機制具有的可調節空間，為再擔保運營機制的動態調整提供理論參考。

2 擔保-再擔保行為策略的演化博弈模型

2.1 系統背景與基本假設

(1)擔保、再擔保機構符合有限理性人假設。這意味著擔保、再擔保機構面對未來的不確定性，難以在一次事件中做出最優決策，需要通過模仿學習較優策略，改進自身的行為。

(2)假設擔保機構的授信額度每年都可以全部用完。當前普遍現象是擔保機構因授信不足，難以滿足中小企業的信貸需求，故此假設符合實際。

(3)假設擔保、再擔保機構為了獲取更多收益而調整自身的行為策略。盡管中小企業信用擔保的宗旨是為解決中小企業的融資困境，擔保、再擔保機構不應以追求盈利為首要目標，但追求適當的收益也是必要的，否則因不斷虧損而倒閉，就談不上扶持中小企業了。

(4)假設政府通過再擔保體系對擔保機構進行風險補貼，未加入再擔保體系的擔保機構不能得到政府的風險補貼。目前我國已基本形成由政策性擔保、互助擔保和商業擔保并存的擔保體系，但并未形成統一的補貼形式，其中，政策性擔保機構可獲得較為穩定的政府補貼，而其他擔保機構卻較難享受政府的資助[14]。但非政策性擔保機構卻占有較大比重，據融資性擔保業務監管部際聯席會議辦公室公布的數據，截至2011年，全國融資性擔保公司共8402家，其中民營及外資控股占81.3%。根據已有研究成果，本文假設通過再擔保機構向擔保機構進行風險補貼符合發展方向，不考慮對未加入再擔保體系的擔保機構進行財政風險補貼符合當前客觀現實。

(5)假設經過考察篩選加入再擔保體系的擔保機構會繼續保持良好的運營狀態，若因落實中小企業信用擔保政策出現收支缺口，可及時得到政府的風險補貼，不至出現虧損，此假設與財政支持中小企業信用擔保體系發展的宗旨一致[14]。

記擔保機構自有資金為K，銀行對其放大倍數為n，保費費率為g1(以擔保金額為基數)，對被擔保人的平均調查監控成本為V1(以擔保金額為基數)，年平均代償率為ω，代償后反擔保物變現占代償金額的比例為C，申請加入再擔保體系的成本為F1，加入再擔保體系后，應付的再擔保費率為g2(以擔保保費為基數)，承擔的風險比例為λ；再擔保機構考察擔保機構的成本為F2，對加入體系的擔保機構平均監控成本為V2(以分擔的再擔保金額為基數)。政府對再擔保機構的補貼為代償金額的a倍，a∈[0,1]，通過再擔保機構對擔保機構的補貼為代償金額的b倍，b∈[0,1]。

在再擔保系統中，對于擔保機構，可選擇的策略集合為A={A1,A2}，其中A1表示申請加入再擔保體系，A2表示不申請加入；而再擔保機構可選擇的策略集合為B={B1,B2}，其中B1表示再擔保機構接受擔保機構的申請，B2表示不接受申請，則可建立擔保、再擔保機構博弈的支付矩陣，如表1所示。

表1 擔保、再擔保機構博弈的支付矩陣

2.2 演化博弈模型的構建

假設擔保機構采取A1策略的比例為p，采取A2策略的比例為(1-p)；再擔保機構采取B1策略的比例為q，則采取B2策略的比例為(1-q)。則擔保機構，采取A1策略的期望收益為E1，采取A2策略的收益為E2，如式(1)、(2)所示：

(1)

E2=nKg1-ωnK(1-C)-V1nK

(2)

則擔保機構的平均期望收益E為：

E=pE1+(1-p)E2

(3)

依據Malthusian動態方程[23]，擔保機構采取A1策略的復制動態方程為：

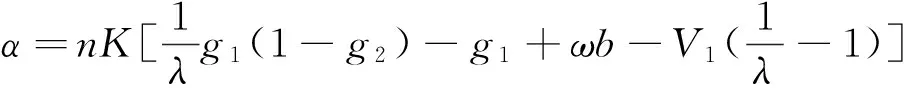
(4)

同理，再擔保機構采取B1策略的收益D1，采取B2策略的收益為D2，平均期望收益D及采取B1策略的復制動態方程G(q)分別如式(5)～(8)所示:

(5)

D2=-pF2

(6)

D=qD1+(1-q)D2

(7)

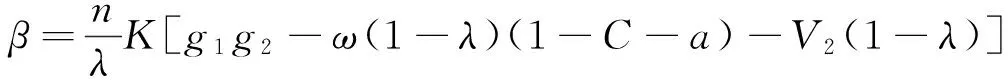
(8)

則擔保、再擔保機構的演化博弈系統可由(4)、(8)式組成的微分方程組進行描述，即：

(9)

其中，p∈[0,1]，q∈[0,1]。

3 再擔保體系演化穩定條件分析

3.1 擔保機構策略選擇的演化博弈分析

根據(4)式，當q=q*=F1/α(即，再擔保機構選擇接受擔保機構加入策略的比例，與擔保機構加入再擔保體系后單位增加收益的申請成本相等)時，p取任何值均為穩定狀態。當q≠q*時，擔保機構的策略選擇將與q值有關，下面根據微分方程穩定性原理分析在此情況下擔保機構的演化穩定策略。

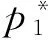
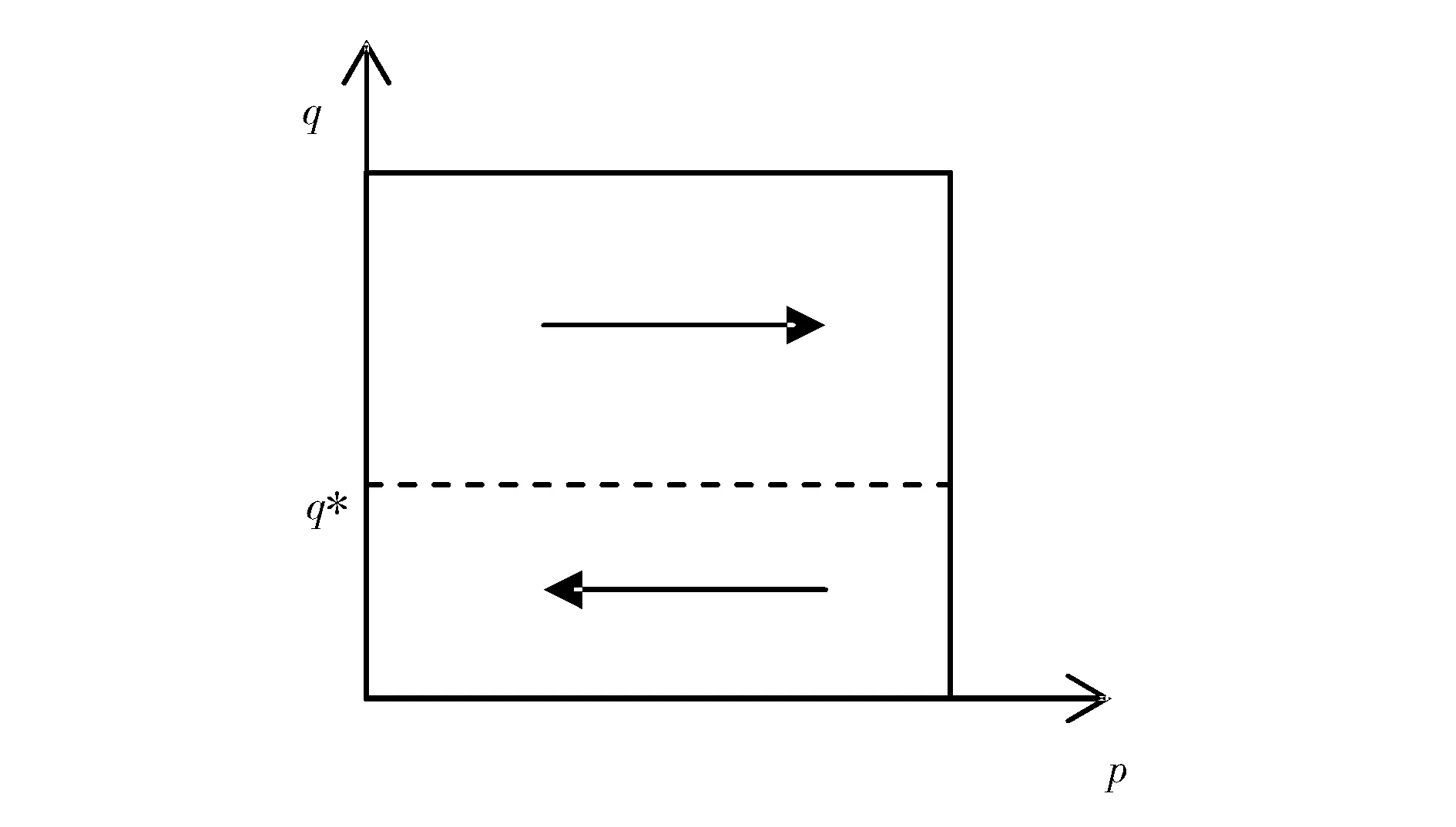
圖1 α>0時擔保機構系統的演化路徑

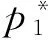
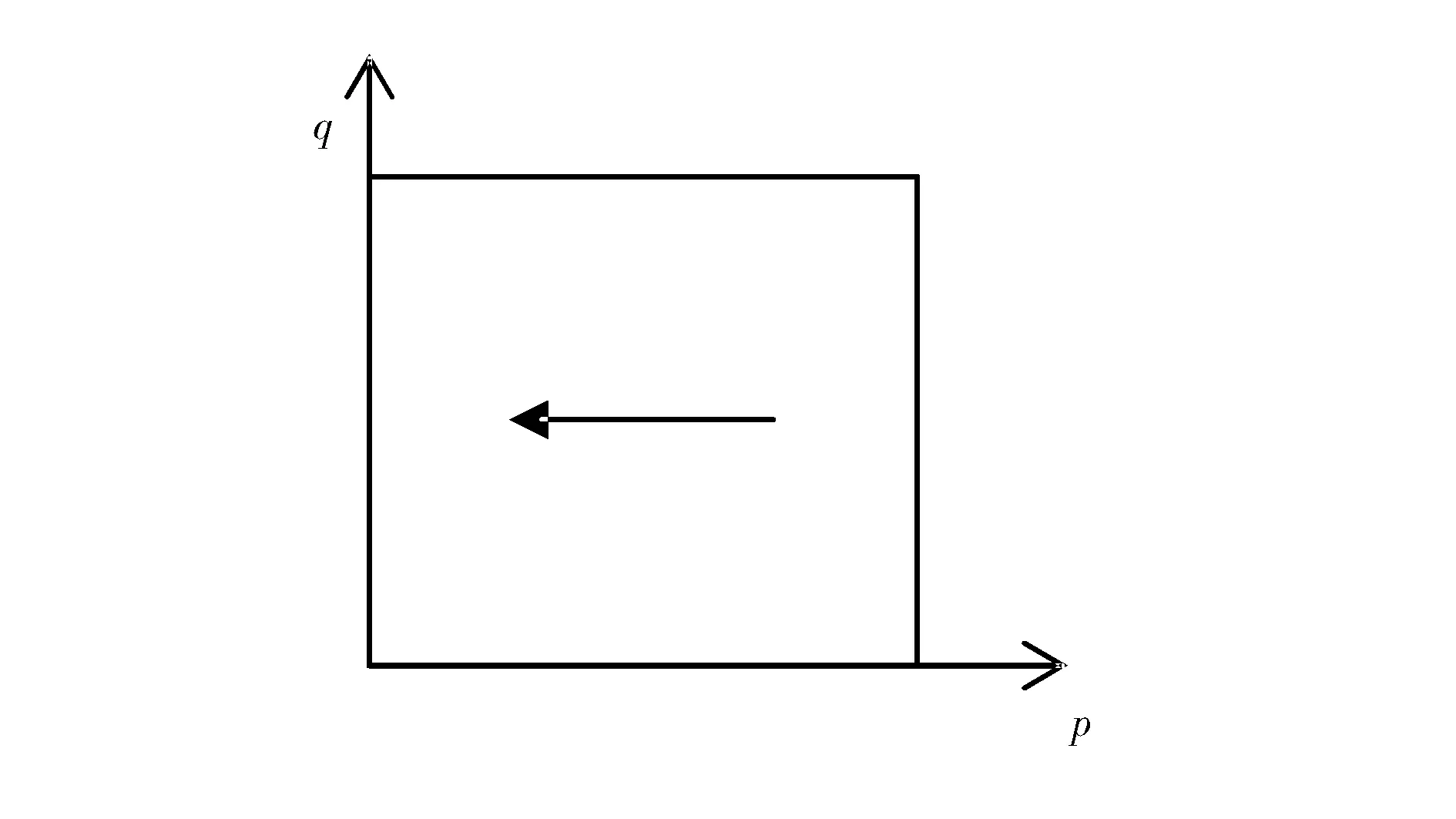
圖2 α<0時擔保機構系統的演化路徑

3.2 再擔保機構策略選擇的演化博弈分析

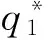
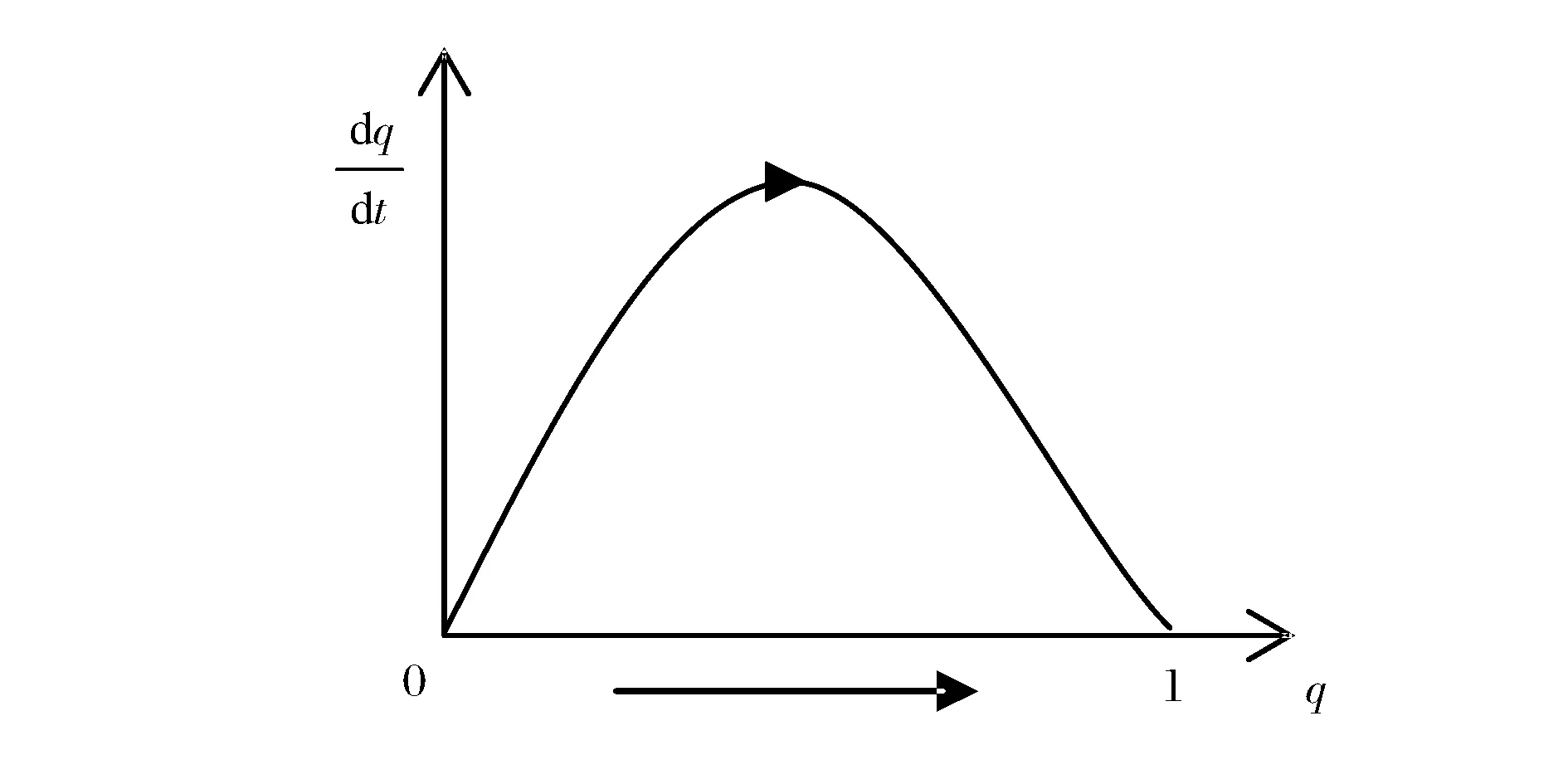
圖3 β>0時再擔保機構策略的演化路徑

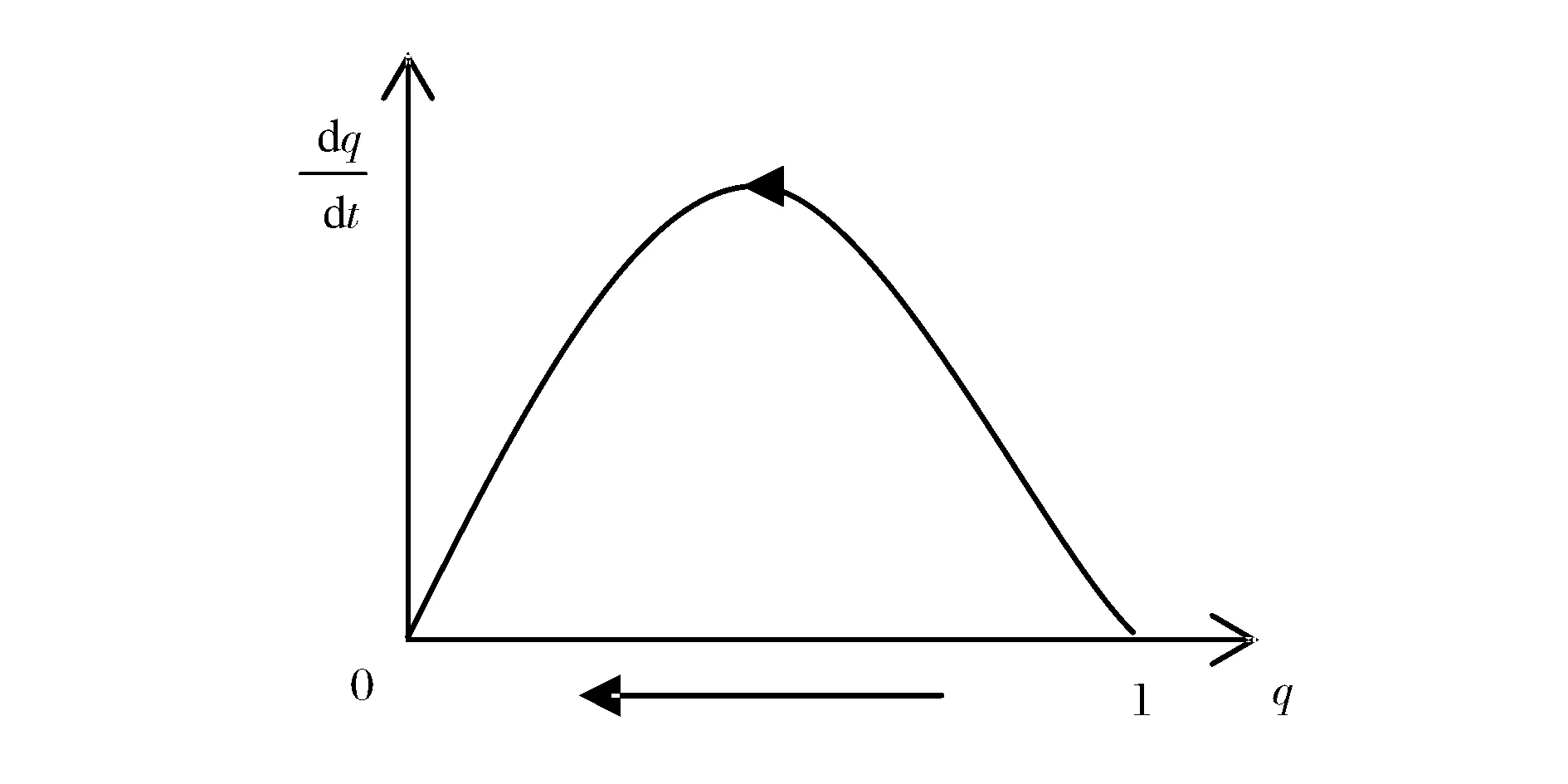
圖4 β<0時再擔保機構策略的演化路徑

3.3 再擔保系統的演化穩定性分析

根據擔保和再擔保機構策略選擇的演化博弈系統對應的微分方程組(9)，可得其對應的雅克比矩陣J、行列式Det(J)、跡Tr(J)如式(10)、(11)、(12)所示：

(10)

Det(J)=(1-2p)(αp-F1)×βp(1-2q)-αβpq(1-p)(1-q)

(11)

Tr(J)=(1-2p)(αq-F1)+βp(1-2q)

(12)

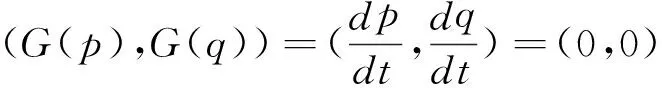
進一步利用雅克比矩陣局部穩定性分析法[24]和中心流形定理[25]對該微分方程組系統進行演化穩定性分析，結果如表2所示。

表2 均衡點的演化穩定性分析

根據表2的結果可知，共有三種可能的演化穩定策略(ESS)：

(1)當擔保機構加入再擔保體系后增加的收益α大于申請成本F1，接受擔保機構加入的再擔保機構初始比例q小于擔保機構加入再擔保體系后單位增加收益的申請成本F1/α，并且，接受擔保機構加入再擔保體系后再擔保機構增加的收益β為負；或者擔保機構加入再擔保體系后增加的收益α、接受擔保機構加入再擔保體系后再擔保機構增加的收益β均為負時，擔保機構將選擇“不申請加入”再擔保體系、再擔保機構將選擇“不接受”加入，再擔保體系將隨著時間的流逝，最終消亡。

(2)當擔保機構加入再擔保體系后增加的收益α為負，而接受擔保機構加入再擔保體系后再擔保機構增加的收益β為正時，擔保機構將選擇“不申請加入”再擔保體系、再擔保機構將選擇“接受”加入，再擔保體系將隨著時間的流逝也會逐漸消亡。

(3)當擔保機構加入再擔保體系后增加的收益α大于申請成本F1，并且接受擔保機構加入再擔保體系后再擔保機構增加的收益β為正時，擔保機構將選擇“申請加入”再擔保體系、再擔保機構將選擇“接受”加入，最后會形成穩定的再擔保體系。

因此，通過擔保、再擔保機構策略選擇的演化分析可知，要使策略組合：擔保機構將選擇“申請加入”再擔保體系、再擔保機構選擇“接受”加入，成為系統的演化穩定策略，必須滿足：再擔保機構接受擔保機構加入再擔保體系后增加的收益β為正，并且，擔保機構加入再擔保體系后增加的收益α大于申請成本F1。這正是在非強制性自動再擔保的市場條件下，再擔保體系能夠穩定演化發展所應具備的條件。當然這些條件，都以本文基本假設為前提。

4 再擔保體系不同運營機制可調整范圍分析

若要保證再擔保體系可持續穩定發展，必須保證β>0且α-F1>0。同時，根據本文的基本假設(5)，政府的風險補貼可及時彌補再擔保體系中擔保機構的收支缺口，再擔保機構接受擔保機構加入再擔保體系后，擔保機構的收益不為負。也即：

在保證再擔保體系穩定發展的基礎上，據(13)～(15)式可進一步分析風險分擔比例、再擔保保費的可調整空間，以及最低政府補貼要求，為再擔保體系不同運營機制的動態調整提供參考。

4.1 風險分擔比例的可調整范圍

在再擔保體系中，如擔保機構自身承擔的風險比例過高，則再擔保體系增信、分險的作用難以發揮；若再擔保機構分擔的風險過高也會導致其入不敷出，難以實現可持續發展。為保證再擔保體系的可持續穩定發展，依據(13)～(15)式，擔保機構承擔的風險比例λ必須同時滿足如(16)、(17)、(18)式的關系：

(19)

對于(17)式，同樣地，政府給予再擔保機構的風險補貼也不可能大于實際代償金額，故ω(1-C-a)≥0，而且監控成本V2>0，則有：

(20)

綜合以上分析，在確保再擔保體系可持續穩定發展的條件下，擔保機構承擔的風險比例λ應滿足：

(21)

擔保機構風險比例λ的下限由(17)式轉化而來，說明擔保機構的最小風險分擔比例由再擔保機構增加的收益β是否為正所控制；而上限由(16)、(18)式轉化而來，意味著擔保機構的最大風險分擔比例由其加入再擔保體系后自身的收益是否為正、以及增加的收益α是否大于申請成本F1共同決定，也即，擔保機構的最小風險分擔比例由外界因素決定，而最大風險分擔比例由自身因素決定，符合客觀現實。特別地，在其它量不變的情況下，代償率ω越高，λ的下限會增大，而上限需要進行比較才能確定。當代償率上升至一定程度，λ可調整的空間將不存在，意味著再擔保體系單靠調整擔保機構承擔的風險比例難以維持穩定，需要采取其它措施。

4.2 再擔保費率的可調整范圍

再擔保保費應根據代償風險、再擔保機構所承擔的風險比例等因素確定，但由于代償風險的不確定性，再擔保保費通常只能依據歷史數據進行估計，因此在保證再擔保體系穩定發展的條件下，討論再擔保費率的可調節范圍，對再擔保體系運營機制的動態調整也同樣具有很強的現實意義。依據(13)～(15)式，再擔保費率應滿足如下關系：

由于n、K、g1>0，且0<λ<1，故再擔保費率g2可調整的范圍如(25)式所示：

(25)

類似地，再擔保最低費率據(23)式轉化而來，由再擔保機構自身因素決定——增加的收益β是否為正；而最高費率據(22)、(24)式轉化而來，受外界因素控制，由加入再擔保體系的擔保機構收益是否為正、以及其增加的收益α是否大于申請成本F1共同決定。特別地，在其它量不變的情況下，代償率ω越高，再擔保費率g2的下限將會增大，而上限需要經過比較才能確定；當代償率上升至一定水平后，g2的可調整空間將不復存在，說明此時僅僅通過調節再擔保保費無法保證再擔保體系的穩定發展，需要采取其它措施。

4.3 最低的政府風險補貼

依據(13)～(15)式，為保證再擔保體系的穩定發展，政府對再擔保、擔保機構的補貼應該滿足如下關系：

由于ω、n、K>0，且0<λ<1，故政府對再擔保機構的補貼應滿足：

(29)

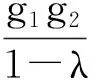
對擔保機構的風險補貼應滿足：

(30)

政府對擔保機構的風險補貼下限由據(26)、(28)式轉化而來，意味著最低風險補貼由擔保機構收益是否為正、以及其增加的收益α是否大于申請成本F1共同決定。

政府風險補貼是再擔保體系穩定發展的最后保障，當擔保和再擔保的風險分擔比例、再擔保保費等運營機制可調整空間不存在時，可根據當期的代償情況，參考(29)、(30)式的最低補償力度，形成動態的政府補償機制。

5 算例分析

為更加直觀展示再擔保體系的演化博弈過程，驗證建立穩定再擔保體系應具備的條件是否正確，展現不同再擔保運營機制的動態調整范圍，下面結合具體算例進行應用分析。

以當前銀行與擔保機構合作的框架為基礎，并參考文獻[16-17]、融資性擔保業務監管部際聯席會議公布的2012年行業數據、中國融資擔保協會整理的相關數據、工信廳聯企業﹝2014﹞65號文件及對部分擔保、再擔保機構調研的數據，假設演化博弈開始時刻，模型中涉及變量的賦值分別為：擔保機構自有資金K=10000萬元，銀行對擔保機構的放大倍數n=4，擔保機構保費費率g1=2%，擔保機構對被擔保人的平均調查監控成本V1=0.6%，年平均賠付概率ω=2%，反擔保物變現占代償金額的比例C=60%，擔保機構申請加入再擔保體系的成本F1=0.5萬元，再擔保機構考察擔保機構的成本F2=0.5萬元，擔保機構加入再擔保體系后承擔的風險比例λ=50%，再擔保費率g2=30%，再擔保機構對擔保機構的平均監控成本V2=0.2%，政府對再擔保機構的風險補貼a=0，對擔保機構的風險補貼b=0，則擔保、再擔保機構的收益矩陣如表3所示，并假設在博弈開始時，至少有一家擔保機構申請加入再擔保體系，即p≠0，再擔保機構也不會拒絕所有的擔保機構加入，即q≠0。

表3 擔保、再擔保機構的收益矩陣

5.1 再擔保體系演化穩定性分析

根據各變量的賦值，可得β=80>0，α-F1=80-0.5=79.5>0，滿足非強制性自動再保市場穩定演化的條件，故此時再擔保體系經過演化，最終可以形成穩定系統。下面進一步驗證再擔保體系穩定演化條件的正確性。

根據(9)式，可知描述該系統演化過程的微分方程組為：

利用maple軟件繪制該系統的相位圖，如圖5所示。從圖5可知，該系統隨時間流逝，最終收斂于p=1、q=1，說明它是系統的演化穩定策略，也即，通過不斷的博弈和模仿學習，擔保機構最終都會選擇“申請加入”再擔保體系、再擔保機構將選擇“接受”加入。該結論與依據再擔保市場穩定演化條件判斷的結果相同，說明再擔保體系穩定演化條件是正確的。

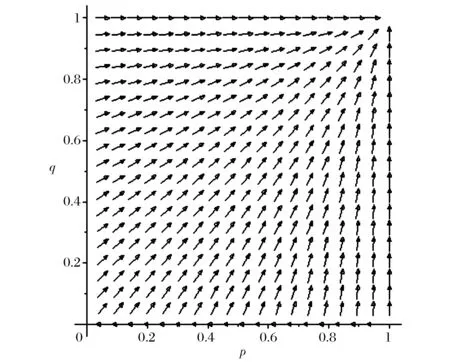
圖5 再擔保系統演化的相位圖

5.2 不同再擔保運營機制的可調整范圍

(1)風險分擔比例的可調整區間

依據(21)式，可得擔保機構承擔的風險比例λ可調整的范圍為：

40%<λ

演化過程中，代償率ω變化時，λ的變化范圍如表4所示。

表4 λ隨代償率變化時的取值范圍

注：表中方框內數據是根據上、下限表達式計算的結果，但該可調整范圍并不存在。

從表4可知，在其它量不變時，隨代償率的上升，擔保機構風險分擔比例λ的下限將增大，說明當代償率上升，適當提高擔保機構承擔的風險比例，可保持再擔保系統穩定發展。其上限此時受條件α-F1>0所控制，而b=0，故其上限并不隨代償率變化。當代償率上升到一定程度，如ω=3%時，λ的可調整區間將不存在，這意味著系統將不會穩定發展。若要保證再擔保體系繼續穩定發展，必須采取其他的措施，如增加政府對擔保、再擔保機構的風險補貼，適當提高擔保保費等。

(2)再擔保費率的可調整范圍

據(25)式，再擔保費率g2的可調整區間為：

25%

演化過程中，代償率ω變化時，g2的變化范圍如表5所示。

表5 g2隨代償率變化時的取值范圍

注：表中方框內數據是根據上、下限表達式計算的結果，但該可調整范圍并不存在。

從表5可知，在其它量不變時，隨代償率的上升，再擔保費率g2的下限將增加，說明當代償率上升時，再擔保機構可適當提高再擔保費率，以保證系統穩定發展；其上限受條件α-F1>0所控制，而b=0，故上限并不隨代償率變化。當代償率增大到一定程度，如ω=3%時，再擔保費率g2的調整區間將不存在，意味著再擔保體系將不能繼續穩定發展，同樣需要采取其它措施，如增加政府對再擔保機構的風險補貼，降低再擔保機構的風險分擔比例，適當提高擔保費率等。

(3)最低政府風險補貼要求

據(29)式，可得：

a>-10%，即取a=0

故在其它量不變時，政府無需對再擔保機構進行補貼，再擔保體系能夠穩定發展。

據(30)式，可得：

b>max(-39.9%,-9.9%)，即取b=0

說明在其它量不變時，政府無需對擔保機構進行補貼，再擔保體系也可穩定發展。

演化過程中，代償率ω變化時，政府對擔保、再擔保機構的最低風險補貼變化走勢如表6所示。

表6 a、b隨代償率變化時的取值范圍

從表6可知，在其它量不變時，隨代償率的上升，為保證再擔保體系的穩定發展，政府需要再擔保機構進行風險補貼；當代償率上升到一定程度，不僅需要對再擔保機構進行補貼，同時還需對擔保機構進行補貼；當代償率較低，如ω≤2%，擔保、再擔保機構在沒有政府補貼的情況下，再擔保體系也能穩定發展。

6 結語

本文假設擔保、再擔保機構為有限理性人，在非強制性再保的市場條件下，利用演化博弈理論分析了擔保、再擔保機構行為策略的演化博弈過程，根據演化穩定策略的形成條件確定了形成穩定再擔保體系應具備的條件；同時，在保證再擔保體系穩定發展的前提下，討論了不同再擔保運營機制所具有的可調整空間。主要得出如下結論：(1)在政府風險補貼能夠及時彌補信用擔保機構虧損的假設前提下，若接受擔保機構加入再擔保體系后再擔保機構增加的收益為正，并且擔保機構加入再擔保體系后增加的收益大于申請成本，則可保證再擔保體系穩定發展；(2)代償率對再擔保運營機制的可調整范圍有重要影響，代償率越高，風險分擔比例、再擔保保費具有的可調節范圍越小，若隨代償率上升不存在調節范圍時，需要對擔保、再擔保機構進行適當的風險補貼，以保證再擔保體系穩定發展。

受當前信用擔保理論和相應數據體系建設的限制，本文僅研究了擔保、再擔保機構具有確定性收益的演化博弈過程。實際上，處于不同時點，因代償率的不確定性，擔保和再擔保機構收益是變化的，因此本模型與現實有一定差距。進一步研究可聚焦于擔保體系數據的進一步完善，對代償率的隨機過程進行定量描述，再利用具有隨機收益的演化博弈形式，分析再擔保體系的穩定演化條件，為再擔保體系穩定發展提供更加貼近實際的理論參考。

[1] 吳建成，黃建. 再擔保體系建設對中小微企業金融服務的影響問題研究[J]. 江蘇社會科學，2014，(5)：91-96.

[2] 曾江候，侯贊. 中小企業再擔保機構運作模式選擇的數理分析[J]. 統計與決策，2007，(21)：137-140.

[3] 文學舟，梅強. 中小企業信用再擔保體系建設及基本框架設計[J]. 企業經濟，2008，(5)：169-171.

[4] 陳曉紅，鐘凡，韓文強. 我國再擔保體系建立模式研究[J]. 理論前沿，2008，(8)：43-44.

[5] ADB (Asian Development Bank), Development of small and medium-sized enterprise credit guarantee companies [M/OL]. [2014-07-07]http://adb.org/sites/default/files/projdocs/2013/46023-001-prc-tar.pdf.

[6] Ju Yonghan, Sohn S Y. Stress test for a technology credit guarantee fund based on survival analysis [J]. Journal of the Operational Research Society, 2015, 66(3): 463-475.

[7] Chang W T, Yu C H, Kuo C J. A prediction of the probability of default of SMEs on the credit guarantee schemes [J]. Journal of Statistics & Management Systems, 2013, 16(2-3): 109-135.

[8] Kuo C J, Chen C M, Sumg C H. Evaluating guarantee fees for loans to small and medium-sized enterprises [J]. Small Business Economics, 2011, 37(2): 205-218.

[9] Oh I, Lee J D, Heshmati A. Evaluation of credit guarantee policy using propensity score matching [J]. Small Business Economics, 2009, 33(3): 335-351.

[10] 于孝建，徐維軍.中小企業信用再擔保各合作方的風險和收益分析[J]. 系統工程，2013，31(5)：33-39.

[11] 薛鈺顯，王東超. 中小企業信用再擔保機構的風險分擔比例研究[J]. 內蒙古社會科學(漢文版)，2013，(3)：103-106.

[12] 林平，袁中紅.信用擔保機構研究[J]. 金融研究，2005，(2)：133-144.

[13] 蔡文宇，陳玉菁. 我國中小企業信用擔保引入政府補貼的可行性探討：基于博弈論的視角[J]. 上海金融，2009，(12)：25-28.

[14] 財政部財政科學研究所課題組. 財政支持中小企業信用擔保政策研究[J]. 經濟研究參考，2010，(31)：2-34.

[15] 馮濤，徐肇成，郭蕾. 財政資助中小企業信用擔保計劃方式的比較研究[J]. 財政研究，2011，(8)：32-34.

[16] 馬國建，張冬華. 中小企業信用再擔保體系經濟效益研究[J]. 軟科學，2010，24(7)：111-115/120.

[17] 梅強，許紅珍. 再擔保體系內銀保風險共擔研究——基于系統動力學[J]. 技術經濟與管理研究，2014，(2)：78-82.

[18] Dindo P, Tuinstra J. A class of evolutionary models for participation games with negative feedback [J]. Computational Economics, 2011, 37(3): 267-300.

[19] Antoci A, Borghesi S, Galeotti M. Environmental options and technological innovation: An evolutionary game model [J]. Journal of Evolutionary Economics, 2013, 23(2), 247-269.

[20] 曾江洪，崔曉云. 基于演化博弈模型的企業集團母子公司治理研究[J]. 中國管理科學，2015，23(2)：148-153.

[21] 李勇建，王治瑩. 突發事件中輿情傳播機制與演化博弈分析[J]. 中國管理科學，2014，22(11)：87-96.

[22] 鄭君君，閆龍，張好雨，何鴻勇. 基于演化博弈和優化理論的環境污染群體性事件處置機制[J]. 中國管理科學，2015，23(8)：168-176.

[23] Webull J. Evolutionary game theory [M]. Princeton: Princeton Press, 1995.

[24] Friedman D. Evolutionary games in economics [J]. Econometric, 1991, 59(3): 637-666.

[25] 馬知恩，周義倉. 常微分方程定性與穩定性方法[M]. 北京：科學出版社，2001.

Analysis on Evolutionary Stability Conditions for SMEs Credit Re-guarantee System

WANG Hui1,2, DENG Xiao-mei1, YANG Wei-hua2, FENG Ke1

(1. Department of Construction Management, Tsinghua University，Beijing 100084, China;2. Military Economics Academy, Wuhan 430035, China)

In countries with stable small and medium-sized enterprises (SMEs) credit re-guarantee system, SMEs credit guarantee companies are required to join the re-guarantee system, and every SMEs credit guarantee agreement is automatically guaranteed by re-guarantee company. However, SMEs credit re-guarantee system is not mandatory in China. An important question is what conditions shall be matched in order to form a stable SMEs credit re-guarantee system through market mechanism rather than compulsory means. To answer the question, an evolutionary game model between SMEs credit guarantee companies and re-guarantee companies was developed to explore the evolutionary stability conditions for SMEs credit re-guarantee system. The evolutionary stable strategies and corresponding conditions of the system were found by utilizing the stability theory of differential equations. Under the premise of steady development of the system, adjustable ranges of operating mechanisms in the re-guarantee system, such as risk sharing proportion, re-guarantee rate and minimum government subsidy, were also further discussed quantitatively. Lastly, a numerical example was provided to verify and applicate the conclusions. The results show that the stable development of SMEs credit re-guarantee system needs two conditions: the incremental payoff of re-guarantee companies has to be positive, and the incremental payoff of guarantee companies has to exceed the filing costs after SMEs credit guarantee companies joining in the SMEs credit re-guarantee system. The results also show that the compensation rate has significant influences on the operating mechanisms in the re-guarantee system. The greater the compensation rate, the lesser the adjustable range of risk sharing proportion and re-guarantee rate. Moderate government subsidy is needed if the adjustable range of risk sharing proportion and re-guarantee rate is absent. The research results provide theoretical references that can be used to improve China’s SMEs credit re-guarantee system.

SMEs credit re-guarantee system; evolutionary stability conditions; adjustable arranges

1003-207(2016)07-0001-10

10.16381/j.cnki.issn1003-207x.2016.07.001

2015-02-07；

2015-10-14

國家自然科學基金面上項目(71473145)

鄧曉梅(1969-)，女(漢族)，四川人，清華大學建設管理系副教授，博士，研究方向：工程擔保、工程管理，E-mail:dengxm@tsinghua.edu.cn.

F830

A