非線性系統自適應魯棒控制器設計

焦鑫，江駒

(南京航空航天大學 自動化學院，江蘇 南京 200016)

?

非線性系統自適應魯棒控制器設計

焦鑫，江駒

(南京航空航天大學 自動化學院，江蘇 南京 200016)

摘要：針對非線性系統模型參數具有不確定性的問題，利用二型模糊邏輯控制器特別適合于解決不確定性問題的優點和特點，提出二型模糊自適應滑模控制方法，設計了具有自適應和魯棒性的非線性系統控制器。首先對非線性系統進行精確線性化，然后選取合適的滑模面，并設計了二型模糊邏輯系統，通過李亞普諾夫穩定性理論分析，得到自適應控制律。通過仿真實例驗證，對比分析并驗證了該控制方法能夠克服不確定性參數的干擾，從而更好地控制非線性系統，使其具有一定的自適應性和魯棒性。

關鍵詞：自適應魯棒控制器；非線性系統；不確定性；二型模糊邏輯系統；自適應性；滑模控制

對非線性系統進行控制器設計時，往往會涉及模型參數不確定的問題，控制器設計的好壞直接決定系統性能和安全[1-2]。例如，飛行器在高空飛行時，由于大氣參數和氣動參數具有不確定性[3]，如果飛行控制器不能很好的適應環境，缺乏一定的魯棒性，那么飛行器的安全性將得不到保證[4-5]。

近年來，國內外學者針對這一問題進行了一定的研究。文獻[6]利用神經網絡參數的在線調整和動態非線性阻尼控制設計了飛行控制器，使飛行控制系統能夠跟蹤給定信號，具有一定的魯棒性。文獻[7]將多輸入系統看作多分布子系統，提出一種自律魯棒自適應分散控制的新方法，結合直接反饋線性化和最優控制，給出了自律最優魯棒自適應分散控制的設計方法。文獻[8]利用確定性魯棒控制方法對參數攝動的最壞情況進行研究，提出一種基于概率估計的H魯棒控制方法，設計出的控制器具有較大的保守性和較高的控制成本。文獻[9]結合高增益的反饋控制和基于在線優化跟蹤控制器的前饋控制針對具有約束條件和不確定性的MIMO系統設計了自適應魯棒控制器。

本文針對非線性系統模型參數不確定問題提出基于二型模糊自適應滑模控制的控制方法，該方法利用二型模糊邏輯控制器特別適合于解決不確定性問題的優點和特點[10-11]，選取合適的滑模面，作為二型模糊控制系統的輸入，經過降型器和去模糊化結算后得到系統輸出，再經過李亞普諾夫穩定性分析得到自適應律，為不確定非線性系統提供了一種新的控制方法。

1精確線性化

考慮不確定性MIMO非線性系統：

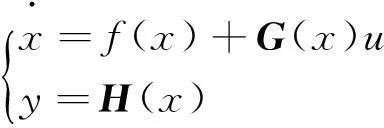
(1)

其中

式中：x∈Rn，u∈Rm，y∈Rm；f，gi是Rn上充分光滑的向量場；hi是充分光滑的標量函數。

考慮第j個輸出yj對時間的導數：

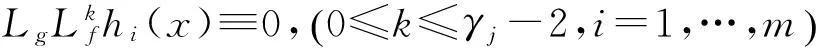
(2)

狀態反饋律為

2二型模糊自適應滑模控制及穩定性分析

對于非線性系統來說，往往涉及模型參數不確定的問題，本文提出二型模糊自適應模糊控制的方法設計控制器，系統結構如圖1所示。

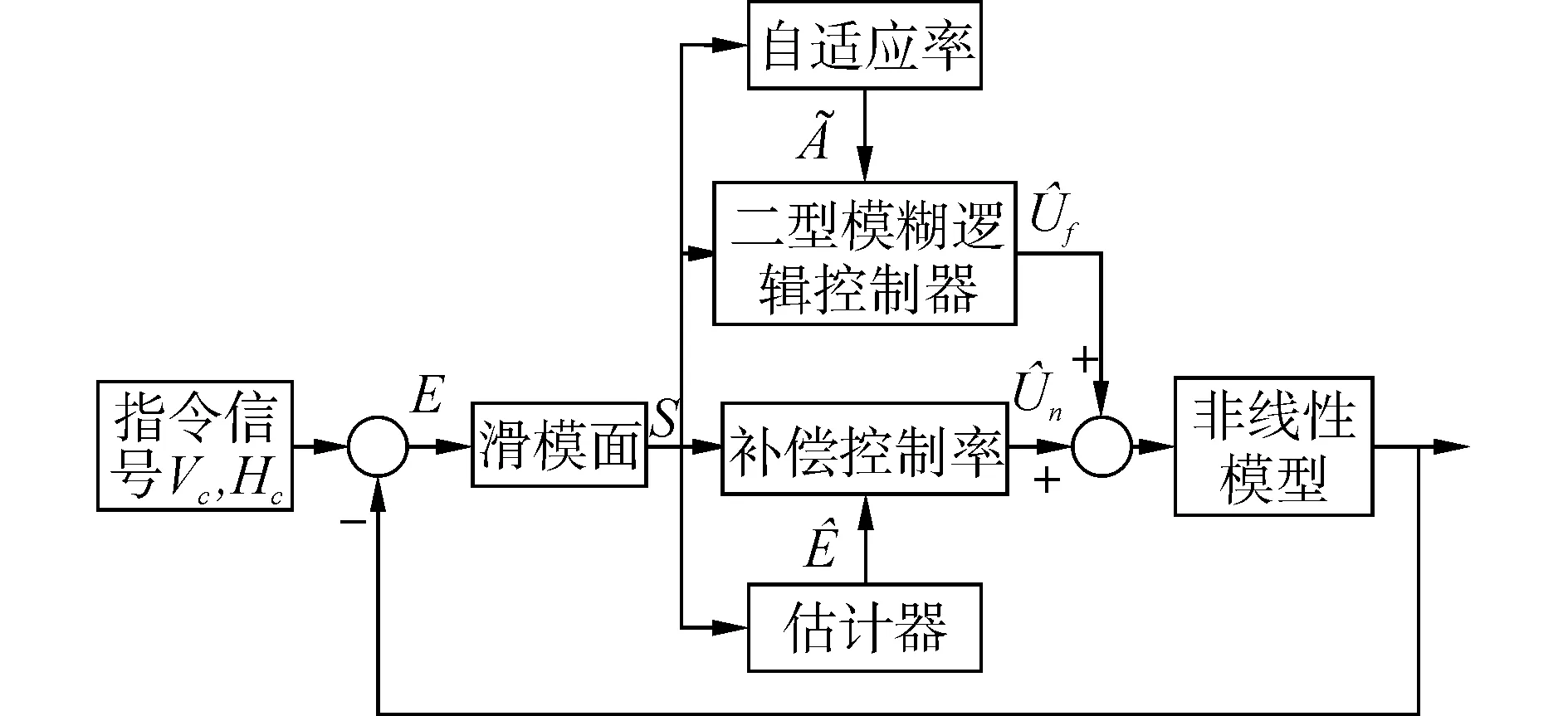
圖1　二型模糊自適應滑模控制的系統結構圖Fig. 1　The system structure of type-2 fuzzy adaptive sliding mode control

圖1中，選取的滑模面作為二型模糊邏輯控制器的模糊輸入，經過模糊推理，降型和解模糊化可以得到二型模糊的清晰輸出，補償控制律用來補償二型模糊控制器的輸出與控制律最優解的差值，使控制器具有較好的魯棒性，估計器用來估計補償控制律中的一些變量值，根據李亞普諾夫穩定性分析可以得到自適應律，使控制器具有自適應性。

2.1滑模面的選取

設K為系統輸入的個數，第j個滑模面為

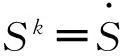
(3)

顯然，當λi選擇合適的參數時，跟蹤誤差將收斂為0，即得到控制律的最優解U*。根據式(2)、(3)可得

(4)

但是在實際中，B(x)的狀態量往往有一些不確定性，所以不能直接得到控制律的最優解U*。當非線性系統具有不確定性時，系統控制律為

(5)

式中：矩陣B(x)為確定性矩陣，即參數為確定的；B(Δx)為不確定矩陣，即參數為不確定的。

2.2二型模糊自適應滑模控制器設計

設二型模糊自適應滑模控制律為Uf，用于估計理想控制律U*。使用具有不確定均值的高斯主隸屬函數作為輸入和輸出的隸屬函數。第i個二型模糊邏輯系統的模糊規則可以描述為

(6)

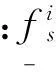
(7)

其中

其中

對于控制律U，二型模糊將被分別用于每個控制器輸入通道，其中S作為二型模糊的輸入，Uf作為二型模糊的輸出。

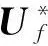
(8)

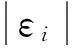
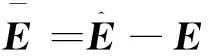
(9)

(10)

所以，二型模糊自適應滑模控制器的控制律可以表達為

(11)

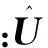
(12)

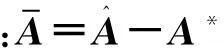
所以，式(2)可重寫為

(13)

根據式(3)、(4)、(13)，可以得到

(14)

2.3穩定性分析

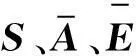
(15)

式(15)的導數為

(16)

根據上式，式(16)可以重寫為

(17)

根據式(17)可以說明系統是穩定的。

為了克服滑模控制的抖振現象，本文將利用飽和函數來代替符號函數：

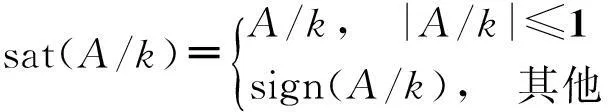
所以，Ujn被重寫為

3仿真實例

3.1仿真條件設定

高超聲速飛行器，具有快時變，嚴重非線性，強耦合，以及模型不確定等特點[13-14]，所以飛行控制系統設計具有很大的難度。根據力和力矩平衡，可建立高超聲速飛行器縱向模型[15]：

式中：V、γ、q、α、h分別表示高超聲速飛行器的速度、軌跡角、俯仰角速率、迎角以及高度；β、ω、ξ分別表示發動機節流閥調定值、固有頻率以及阻尼系數；m、μ、r、My、Iy分別表示質量、萬有引力常量、地球半徑、俯仰力矩系數以及慣性力矩系數。升力L、阻力D、推力T如下

式中：CL、CD、CT分別表示升力系數、阻力系數、推力系數，ρ、s分別表示空氣密度、機翼參考面積。

參數不確定性主要體現在模型參數和氣動參數的不確定。本文中，不確定參數作為外加變量加入正常變量中用于控制器設計。主要參數如下：

表1分別列出滑模面SV和Sh的初始隸屬函數參數值。

表1　滑模面SV、Sh的初始隸屬函數參數值

根據本文所論述的方法，可以得到控制律：

其中

3.2速度信號和高度信號階躍響應

在速度信號階躍響應仿真驗證中，速度指令信號40 m/s的階躍信號，仿真結果如圖2所示。

在高度信號階躍響應仿真驗證中，高度指令信號為40 m的階躍信號，仿真結果如圖3所示。

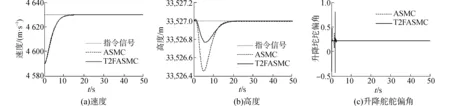
圖2　速度指令為40 m/s的階躍響應Fig. 2　Response to a 40 m/s step-velocity command

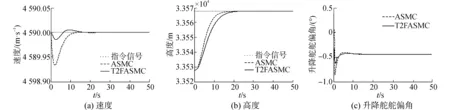
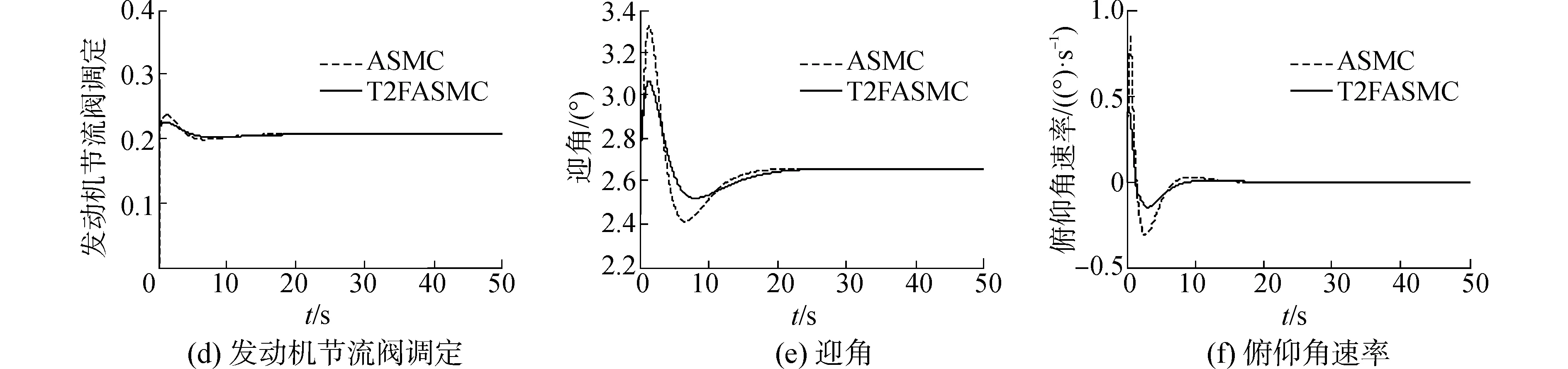
圖3　高度指令為40 m的階躍響應Fig. 3　Response to a 40 m step-altitude command

4結論

從速度信號階躍響應和高度信號階躍響應兩種控制效果來看，對比文獻[16]所提出的自適應滑模控制器，本文所提出的具有自適應魯棒性的二型模糊自適應滑模控制器具有明顯的優勢。

1)對于速度信號階躍響應，高度、升降舵偏角、發動機節流閥調定、迎角、軌跡角、俯仰角速率以及滑模面的變化量都明顯小于自適應滑模控制器控制效果的變化量，尤其是升降舵偏角變化量和俯仰角速率變化量，這不僅說明本文所論述的控制器魯棒性更強，而且從工程角度來說，能夠使飛行器的機動性更強，也更節約能源。

2)對于高度信號階躍響應，雖然二型模糊自適應滑模控制器比自適應滑模控制器的響應速度略慢，但是控制效果優勢明顯，其中，速度、升降舵偏角、發動機節流閥調定、迎角、軌跡角、俯仰角速率以及滑模面的變化量都明顯小于自適應滑模控制器控制效果的變化量，從而使高超聲速飛行器的穩定性更好，魯棒性更強，而且能夠提高飛行器的機動性，也更節約能源。

總之，從仿真結果可以看出，二型模糊自適應滑模控制能夠提高非線性系統的穩定性，跟蹤性能以及魯棒性。

參考文獻：

[1]CHANG Y H, CHAN Weishou. Adaptive dynamic surface control for uncertain nonlinear systems with interval type-2 fuzzy neural networks[J]. IEEE transactions on cybernetics, 2014, 44(2): 293-304.

[2]SENTHILKUMAR D, MAHANTA C. Identification of uncertain nonlinear systems for robust fuzzy control[J]. ISA transactions, 2010, 49(1): 27-38.

[3]ZHANG Ruimin, SUN Changyin, ZHANG Jingmei, et al. Second-order terminal sliding mode control for hypersonic vehicle in cruising flight with sliding mode disturbance observer[J]. Journal of control theory and applications, 2013, 11(2): 299-305.

[4]GAO Gang, WANG Jinzhi, WANG Xianghua. Robust tracking control for an air-breathing hypersonic vehicle with input constraints[J]. International journal of systems science, 2014, 45(12): 2466-2479.

[5]FIORENTINI L, SERRANI A, BOLENDER M A, et al. Nonlinear robust adaptive control of flexible air-breathing hypersonic vehicles[J]. Journal of guidance, control, and dynamics, 2009, 32(2): 402-417.

[6]陳龍勝. 綜合非線性魯棒飛行控制系統設計[J]. 南昌航空大學學報: 自然科學版, 2014, 28(1): 14-20.

CHEN Longsheng. Design of robust adaptive flight controller based on nonlinear dynamics[J]. Journal of Nanchang hangkong university: natural sciences, 2014, 28(1): 14-20.

[7]谷志鋒, 朱長青, 邵天章. 分布式多輸入系統的自律魯棒自適應分散控制[J]. 控制與決策, 2014, 29(9): 1545-1552.

GU Zhifeng, ZHU Changqing, SHAO Tianzhang. Autonomous robust adaptive decentralized control for distributed multi-input system[J]. Control and decision, 2014, 29(9): 1545-1552.

[8]謝蓉, 王新民, 鞏建英. 范數有界型參數不確定性系統的概率魯棒 控制方法[J]. 控制與決策, 2014, 29(7): 1301-1305.

XIE Rong, WANG Xinmin, GONG Jianying. Probabilistic robust control method of norm-bounded parameter uncertainty system[J]. Control and decision, 2014, 29(7): 1301-1305.

[9]LU Lu, YAO Bin. Online constrained optimization based adaptive robust control of a class of MIMO nonlinear systems with matched uncertainties and input/state constraints[J]. Automatica, 2014, 50(3): 864-873.

[10]MENDEL J M, JOHN R I, LIU Feilong. Interval type-2 fuzzy logic systems made simple[J]. IEEE transactions on fuzzy systems, 2006, 14(6): 808-821.

[11]LIANG Qilian, MENDEL J M. Interval type-2 fuzzy logic systems: theory and design[J]. IEEE transactions on fuzzy systems, 2000, 8(5): 535-550.

[12]YANG Fang, YUAN Ruyi, YI Jianqiang, et al. Direct adaptive type-2 fuzzy neural network control for a generic hypersonic flight vehicle[J]. Soft computing, 2013, 17(11): 2053-2064.

[13]WANG Qian, STENGEL R F. Robust nonlinear control of a hypersonic aircraft[J]. Journal of guidance, control, and dynamics, 2000, 23(4): 577-585.

[14]WANG Qian, STENGEL R F. Robust nonlinear flight control of a high-performance aircraft[J]. IEEE transactions on control systems technology, 2005, 13(1): 15-26.

[15]SUN Haibin, LI Shihua, SUN Changyin. Finite time integral sliding mode control of hypersonic vehicles[J]. Nonlinear dynamics, 2013, 73(1/2): 229-244.

[16]XU Haojian, MIRMIRANI M D, IOANNOU P A. Adaptive sliding mode control design for a hypersonic flight vehicle[J]. Journal of guidance, control, and dynamics, 2004, 27(5): 829-838.

Design of an adaptive robust controller for nonlinear system

JIAO Xin, JIANG Ju

(College of Automation Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 200016, China)

Abstract：To address the problem of a nonlinear system with uncertain parameters, in this paper we propose a type-2 fuzzy-sliding-mode control method for designing an adaptive robust controller for nonlinear systems. We based the proposed method on the characteristics of type-2 fuzzy logic systems, which are especially adapted for solving uncertainty problems. For this novel method, we first precisely linearized the nonlinear model. Then, we designed a type-2 fuzzy logic system with selected appropriate sliding mode surfaces to overcome the uncertain parameters. To rapidly stabilize the system, we also designed adaptive laws by direct constructive Lyapunov analysis. A comparison of the simulation results indicates that the proposed control scheme can overcome uncertainties and better control the nonlinear system, thus making the whole system more adaptive and robust.

Keywords：adaptive robust controller； nonlinear system; uncertainty; type-2 fuzzy logic system; adaptivity; sliding mode control

中圖分類號：TP273

文獻標志碼：A

文章編號：1006-7043(2016)03-402-06

doi:10.11990/jheu.201411020

作者簡介：焦鑫(1986-)，女，博士研究生;江駒(1963-)，男，教授，博士生導師.通信作者：焦鑫，E-mail: jiaoxin_mengqu@163.com.

基金項目：國家自然科學基金資助項目(61304223)；江蘇省普通高校研究生科研創新基金資助項目(CXZZ13_0170)；南京航空航天大學校博士學位論文創新與創優基金資助項目(BCXJ13-06).

收稿日期：2014-11-10.

網絡出版地址：http://www.cnki.net/kcms/detail/23.1390.u.20151224.1405.002.html

網絡出版日期：2015-12-24.