分拆方法在證明不等式中的應用例談
2016-05-05 02:21:55周輝
中學數學研究(江西) 2016年3期
?
分拆方法在證明不等式中的應用例談
南昌大學附屬中學(330047)周輝
分拆在不等式的證明中非常重要.分拆的目的就是為使用常用的不等式營造一個和諧的環境.下面筆者以2015年國際數學奧林匹克的一些典型試題為例,充分展示分拆方法在證明不等式中的作用.
例1(2015年阿塞拜疆數學奧林匹克)
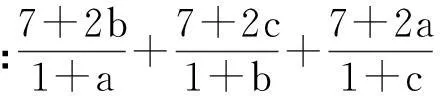
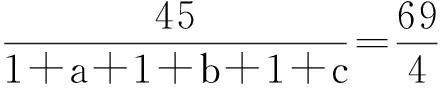
評注:合理的分拆,為放縮和應用柯西不等式創造了條件.
例2(2015年澳大利亞數學奧林匹克)
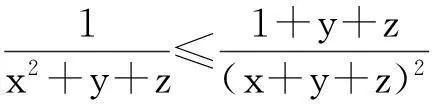
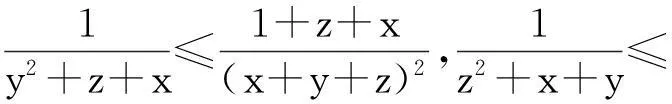
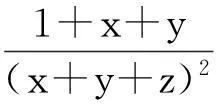
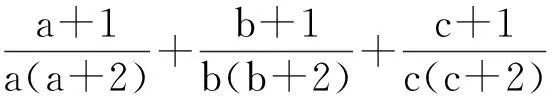
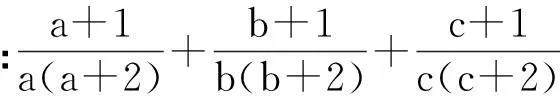
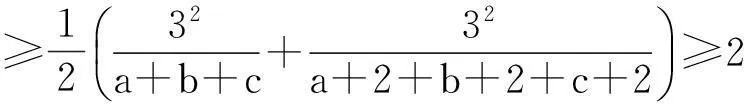
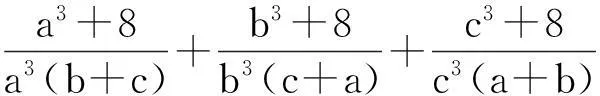

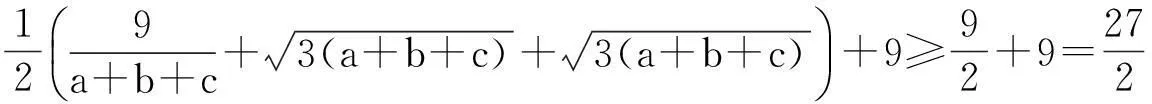
評注:多項的分拆放縮,目標是使取等的條件一致.
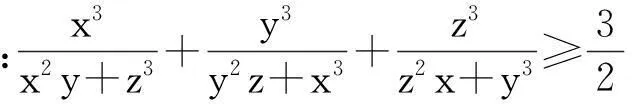
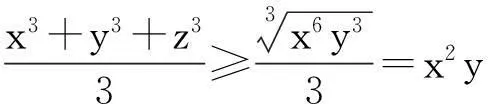


綜上,原不等式成立.
評注:第一次的分拆,是將分母升冪,為后續的換元打下基礎.
例6(2015年阿塞拜疆數學奧林匹克)

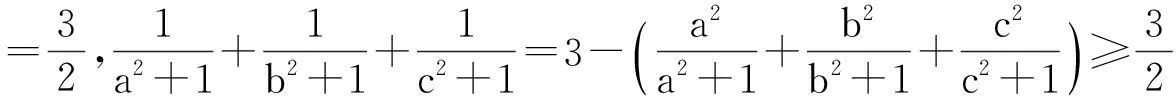
例7(2015年摩爾多瓦數學奧林匹克)已知a,b,c是滿足abc=1的正數,求證:
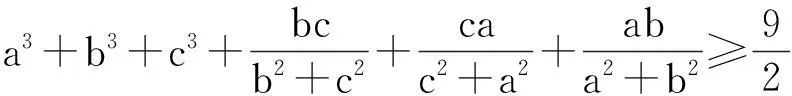
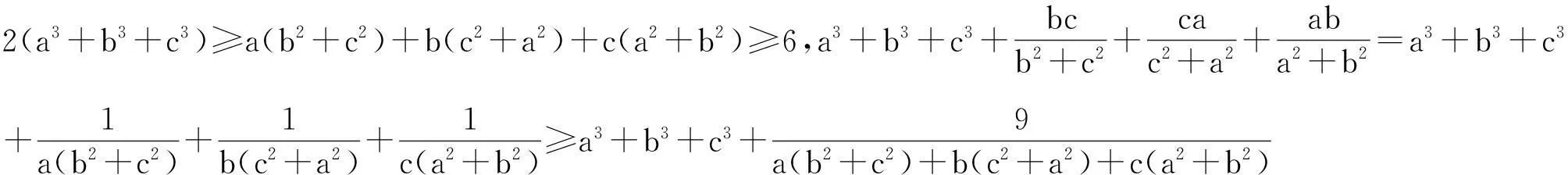
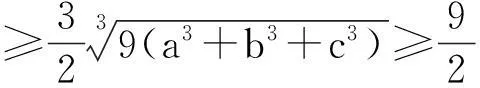
猜你喜歡
學苑創造·A版(2019年5期)2019-06-17 01:14:21
兒童故事畫報(2019年5期)2019-05-26 14:26:14
新民周刊(2016年15期)2016-04-19 18:12:04
新民周刊(2016年15期)2016-04-19 15:47:52
Coco薇(2016年2期)2016-03-22 02:42:52
Coco薇(2015年1期)2015-08-13 02:47:34
小雪花·成長指南(2015年7期)2015-08-11 15:03:12
小雪花·成長指南(2015年4期)2015-05-19 14:47:56
漫畫月刊·炫版(2014年3期)2014-05-27 04:17:21
中學生數理化·高二版(2008年7期)2008-06-15 01:31:20

