一類高考壓軸題中的不等式證明策略

?

一類高考壓軸題中的不等式證明策略

江蘇省昆山中學(215300)繆林

在各地高考壓軸題中常見這樣的不等式“a1+a2+…+an>F(n)”或“ a1·a2·…·an>F(n)”的判斷或論證，這類問題涉及函數、數列、不等式等綜合知識，對數學知識技能、數學思想意識的要求非常之高. 命題意圖是對前面幾個小問中獲得的結論進行“二次開發”，獲得一個新的命題，再利用這一命題進行論證，解題技巧強，思維要求高，因此，絕大多數同學望而卻步. 若從“看成”角度探尋解題策略，常常可以化難為易迎刃而解.

所謂 “看成”即是通過對數學問題表征的分析研究，將數學對象賦予(視著)新的數學意義，并嘗試將其激活為某類問題模型的過程. “看成策略”即是在“看成”的基礎上選擇解題方向，擬定解題計劃，然后執行相應的解題程序.這是一種有目的的思維活動，但并不遵循嚴格的規則，通常是憑知識經驗和審美判斷，帶有一定程度的猜測性和預見性，常常需要多角度嘗試“看成”，合理“看成”路徑的選擇是解題成功的關鍵.

1、將F(n)看成數列前n項之和

例1(2014年陜西(理)第21題) 設函數F(x)=ln(1+x)，G(x)=xF ′(x)，x≥0，其中F ′(x)是F(x)的導函數．

(1)令G1(x)=G(x)，Gn+1(x)=G(Gn(x))，n∈N+，求Gn(x)的表達式；

(2)若F(x)≥aG(x)恒成立，求實數a的取值范圍；

(3)設n∈N+，比較G(1)+G(2)+…+G(n)與n-F(n)的大小，并加以證明.

思路探求：(1),(2) 兩小問略；

由于S(n)是數列{G(n)}的前n項之和，故可嘗試把T(n)看成數列{bn}前n項之和，若能比較G(n)與bn之大小即可獲得結論．

評析：對問題表征的差異分析是實現“看成”的關鍵. 左式是n項之和，而右式僅二項，減少差異的兩種最為自然的想法是：其一、對左式求和——“合”，但在此處顯然是不可能的；其二、將右式轉化為某數列前n項之和——“分”，由此獲得“看成”的策略：將T(n)看成某數列前n項和，進而將問題轉化為比較兩數列相應項的大小，這遠比創造性地運用第(2)小問獲得的結論，通過對左式中的通項進行放縮轉化為可求和的數列進行求和再比較大小更為簡捷明晰．

2、將F(n)看成數列前n項之積

例2(2015年安徽理科題)設n∈N*,xn是曲線y=x2n+3+1在點(1,2)處的切線與x軸交點的橫坐標.

(1)求數列{xn}的通項公式；

3、將“常數”看成無窮遞縮等比數列所有項之和或數列的前n項之和

例3(2014新課標理科Ⅱ理)已知數列{an}滿足a1=1，an+1=3an+1.

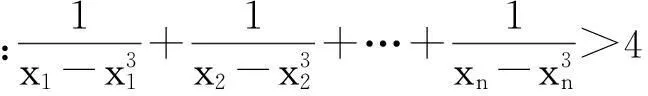
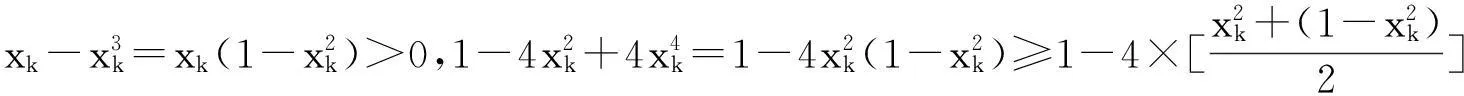
在差異分析觀點之下，上述措施不是一個妙手偶得的特殊技巧，而是一個策略思想的具體實施.

參考文獻

[1]羅增儒. 數學解題學引論[M]. 西安：陜西師范大學出版社，1997.

[2]齊建民. 從“見山是山”到“見山不是山”[J]. 中學數學研究(江西)，2014(4)：28-30.

[3]繆林. 目標引領 理性探索[J]. 中學數學教學參考，2011(11)：37-40.