轉化思想提高實效

田恒梅

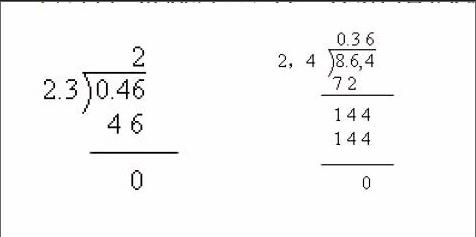
【課本研讀】

“除數是小數的除法”是蘇教版數學教材（2013年出版）五年級上冊第五單元“小數乘法和除法”的內容。本單元共有14個例題，而例10是教學“除數是小數的除法”的起始課。教材編排力求結合具體情境，學生經歷自主探索除數是小數的除法計算方法的過程，并能夠比較熟練地進行其筆算和簡單的口算。“除數是小數的除法”是“除數是整數的小數除法”的跨越和發展。教材只提供了短短的一行文字和一幅雞蛋圖（已知總價和單價），求數量的實際問題（例10），且除數是整數的小數除法還是前面例4的教學內容，學習出現了間隔，學生難免會遺忘；對于教學一線老師們來說，合理設計教學流程，把握教學重點，提高課堂教學有效性，也具有一定難度。在家常課中往往會出現“就題論題”，只是死死地強化學生把除數轉化為整數，缺乏推理的根基，導致算理算法梳理不清，教學效果不理想。因此，常常會聽到“‘除數是小數的除法教師難教、學生難學”的聲音，是小學數學計算教學一個瓶頸。

實際上，除數是小數的除法與整數的除法在計算方法上具有一致性，關鍵是在運用轉化的數學思想上，要以學生的認知發展水平和已有經驗為基礎，根據商不變性質把除數由小數轉化成整數，再進行計算。教學時要放慢節奏，放緩坡度，重點應該放在“把除數由小數轉化成整數”上，而落實這個重點需要在各個教學環節中凸顯數學轉化思想。

【教學實踐】

一、回顧再現感受轉化

師：知識是相互聯系的，今天的學習就讓我們先從回顧學過的除法計算開始……

回顧1：關于整數除法計算。出示：56000÷800=

1.這是一道我們學過的整數除法，請口算結果。學生交流：56000÷800如何計算的？（變成560÷8來口算）

轉化

2.引導總結：難———→易

回顧2：關于小數除法計算。出示3千克蘋果9.6元。每千克多少元？（例4部分內容）

3.學生列式，豎式計算出結果。追問：在豎式計算時要注意些什么？

4.師引導學生回顧：現在大家都能很快說出小數除法的計算結果，但當我們第一次遇到它時，它對于我們來說是一個不會的問題，下面我們回顧一下當時學習時解決這個問題的過程。出示下圖：

我們先把它轉化已會的知識來解決（引出“未知轉化成已知”），問題雖然解決了，但這種方法有其特殊性，我們要尋找能對所有小數除以整數都適用的一般方法（引出“特殊算法轉化成一般算法”）。

二、新知探究體驗轉化

（一）體驗口算轉化

1.出示：鉛筆每支0.5元，2.5元可以買幾支？

引導學生圍繞“2.5÷0.5與我們學過的小數除法有什么不同”這個問題展開自我探究，交流方法。

2.交流、提煉、板書：

轉化

除數是整數的除法←—除數是小數的除法

關注除數

3.對比中體驗：0.12÷0.6和0.6÷0.12

（1）先出示：0.12÷0.6，問：怎么把除數轉化成整數？（學生交流得出被除數和除數的小數點同時向右移動一位，即乘10，就轉化成1.2÷6）

（2）再出示：0.6÷0.12，問：你會轉化了嗎？（學生交流得出被除數和除數的小數點同時向右移動兩位，即乘100，轉化成60÷12）

（3）引導對比：兩個除法式子都是同樣的數“0.12”和“0.6”，只是位置發生變化，為什么在轉化第一個式子的被除數和除數同時乘10，而第二個式子同時乘100呢？（得出：在轉化時應關注除數。）

（二）體驗筆算轉化

1.出示例10.審題后交流列式：7.98÷4.2.

2.師：能口算出它的結果嗎？（生搖頭），估算一下它的結果？（大約是2千克）

3.師：要算準確商，那我們請什么來幫忙？（豎式）

先不算，只寫出豎式并轉化。組織學生重點交流轉化過程和寫法，然后再算出結果。

4.規范豎式轉化過程：

5.及時內化。寫出下面小數除法豎式轉化過程不必計算結果：

0.736÷0.82.86÷0.22

三、鞏固練習活用轉化

1.判斷練習：

（1）直覺觀察判斷，說出判斷理由。

0.46÷2.3=286.4÷2.4=0.36

（2）仔細觀察豎式，分析錯因。

2.嘗試練習：0.7[4.83] 0.56[0.196]

3.拓展練習：出示189÷900、1.2÷0.25如何轉化最簡單，且能口算出結果。（交流后得到：第1題被除數和除數同時除以100，轉化成：1.89÷9；第2道題被除數和除數同時乘4，轉化成4.8÷1）

四、整理反思提升轉化

師：今天，我們解決了除數是小數除法的計算問題，給你留下印象深刻的是什么？對，是“轉化”幫助了我們，誰來評價評價我們這個朋友？

師：是的，“轉化”是一種解決問題的策略，也是數學思想。它能化難為易，化繁為簡，化未知為已知……今后，我們在數學學習中還會應用到它，包括在我們生活中。

【教學反思】

為了突破本課時常規教學低效這個瓶頸，我根據2011版課程標準“四基”目標，試圖解決數學知識與數學思想之間相互融合的問題，從而達到凸顯轉化思想、提高課堂教學實效的目的。

1.喚醒學生已有知識技能，凸顯數學轉化思想

相對于知識技能，數學思想更為內隱，所以更需要滲透，即要在學生學習中予以捕捉、放大、傳遞。為了學習更加有效，本課時教學，我努力將轉化思想的滲透體現于教學環節之中，從而使轉化思想得以凸顯。例如，在復習環節，安排了“回顧1”和“回顧2”，舍得時間來放慢節奏，放緩坡度。引導學生重點回顧了已學的整數除法和小數除法（除數是整數），但展開的方式不只是讓學生去做題，而是引導學生帶著思考去進行，努力激活學生已有、潛在的轉化經驗。再如，在教學筆算豎式除法時，學生已有了除法豎式知識技能，不在機械的計算上花更多時間，而是引導學生關注豎式轉化過程，從而突出了本節課計算教學的重點、難點。

2.利用明暗線交織展開教學，提高課堂教學實效

本課時教學一是以“雙基”教學為明線，回顧再現（復習）→新知探究（新授）→鞏固練習（鞏固）→整理反思（總結）；二是以轉化思想為暗線，感受轉化→體驗轉化→活用轉化→提升轉化。本課教學努力實現兩條明暗線的相互交融，共同推進教學的展開。這樣不但能引發學生的數學思考，上出了數學味，而且使轉化的數學思想植入學生心中。例如，在對比體驗：0.12÷0.6和0.6÷0.12的教學中，既關注了學生如何口算除數是小數除法的思維度（這根“雙基”的明線），更聚焦了本節課小數除法計算方法的本質（這根思想的暗線），讓學生在富有辨證意味的問題中展開對比思考，自然體驗到“除數是小數的除法應以除數為標準進行轉化”。教學各個環節能緊扣“轉化”的需要，尋求商不變性質這一解決問題的“理論依據”。這樣抓住了除數是小數的除法的本質，不在豎式計算上設置過多的人為障礙，降低學生學習的難度，讓學生學得更輕松，才能使提高課堂教學效度落到實處。

【作者單位：來安縣實驗小學 安徽】