區(qū)間上二部可圖序列刻劃定理的推廣

郭紀(jì)云，蔡白光

(海南大學(xué)信息科學(xué)技術(shù)學(xué)院, 海南 海口 570228)

?

區(qū)間上二部可圖序列刻劃定理的推廣

郭紀(jì)云，蔡白光

(海南大學(xué)信息科學(xué)技術(shù)學(xué)院, 海南 海口 570228)

摘要：設(shè)Pm=p1,…,pm及Qn=q1,…,qn是兩個(gè)由非負(fù)整數(shù)構(gòu)成的不增序列. 如果存在一個(gè)簡(jiǎn)單X,Y-二部圖G使得X中的頂點(diǎn)的度分別為p1,…,pm且Y中的頂點(diǎn)的度分別為q1,…,qn，那么稱序列對(duì)(Pm,Qn)是二部可圖的, 并稱二部圖G為(Pm,Qn)的一個(gè)實(shí)現(xiàn). 如果(Pm,Qn)二部可圖且任何兩個(gè)來(lái)自不同部集的頂點(diǎn)之間最多關(guān)聯(lián)t條邊，那么稱(Pm,Qn)是t-二部可圖的, 并稱(Pm,Qn)的實(shí)現(xiàn)為t-二部圖. Gale和Ryser分別獨(dú)立地給出了關(guān)于二部可圖序列的刻劃定理. Garg等人考慮了區(qū)間上的二部可圖序列，并給出相應(yīng)刻劃. 此研究將其刻劃由1-二部推廣至圖t-二部圖.

關(guān)鍵詞：二部可圖序列；區(qū)間上二部可圖序列； t-二部可圖序列

1相關(guān)知識(shí)

設(shè)Pm=p1,…,pm及Qn=q1,…,qn是兩個(gè)由非負(fù)整數(shù)構(gòu)成的不增序列. 如果存在一個(gè)簡(jiǎn)單X,Y-二部圖G使得X中的頂點(diǎn)的度分別為p1,…,pm且Y中的頂點(diǎn)的度分別為q1,…,qn，那么稱序列對(duì)(Pm,Qn)是二部可圖的, 并稱二部圖G為(Pm,Qn)的一個(gè)實(shí)現(xiàn). Gale[1]和Ryser[2]分別給出了經(jīng)典的關(guān)于二部可圖序列的刻劃定理.Garg等人[3]則考慮了區(qū)間上的二部可圖序列，并給出如下定理.

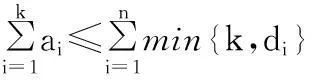
稱由非負(fù)整數(shù)構(gòu)成的不增序列對(duì)(Pm,Qn)是t-二部可圖的, 如果(Pm,Qn)二部可圖且任何兩個(gè)來(lái)自不同部集的頂點(diǎn)之間最多關(guān)聯(lián)t條邊. 此時(shí), (Pm,Qn)的實(shí)現(xiàn)稱為t-二部圖.本文給出一個(gè)區(qū)間上t-二部可圖序列刻劃定理, 從而將區(qū)間上二部可圖序列的刻劃從1-圖推廣至t-圖.

定理1.2設(shè)L1=([a1,b1],…,[am,bm])和L2=([c1,d1],…,[cn,dn])是兩個(gè)由非負(fù)整數(shù)構(gòu)成的區(qū)間序列, 其中a1≥…≥am且c1≥…≥cn, 則存在一個(gè)t-二部圖G,其部集為X={x1,…,xm}和Y={y1,…,yn}, 使得ai≤dG(xi)≤bi,1≤i≤m且cj≤dG(yj)≤dj,1≤j≤n當(dāng)前且僅當(dāng)對(duì)于每一個(gè)整數(shù)k1,1≤k1≤m,有

(1)

且對(duì)于每一個(gè)整數(shù)k2,1≤k2≤n,有

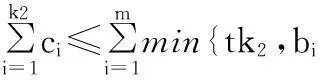
(2)

2定理1.2的證明

必要性. 設(shè)G是滿足條件的t-二部圖, 其部集為X={x1,…,xm}和Y={y1,…,yn}.考慮關(guān)聯(lián)到X中的k1個(gè)頂點(diǎn)的所有邊. 由于G是t-二部圖, 因此每個(gè)yj∈Y最多關(guān)聯(lián)到這些邊中的tk1條, 而且yj也最多關(guān)聯(lián)到這些邊中的dG(yj)條. 于是, 對(duì)于每一個(gè)整數(shù)k1,1≤k1≤m, 有

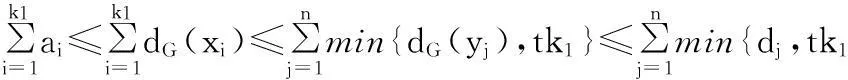
因此(1)式成立. 同理可證(2)式亦成立.

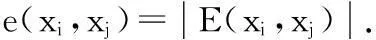
情形(1)對(duì)于某個(gè)j和k(k>r), e(yj,xk)≥1, 且存在某個(gè)l(l≤r)使得e(yj,xl)e(v,xr).

情形(2)對(duì)于某個(gè)j和l(l≤r), d(yj)e(v,xr).

若以上兩種情形均不能應(yīng)用, 則

(3)

因?yàn)閐(xi)=ai,1≤i

在G′中, 定義一個(gè)臨界指標(biāo)s, 它是滿足條件d(yj)≥cj,1≤j

情形(3)對(duì)于某個(gè)i(ie(v,ys).

若以上三種情形均不能應(yīng)用, 則類似于(3)式, 可得d(ys)=cs. 令s的值增加1, 重復(fù)上述步驟, 可構(gòu)造出想要的t-二部圖.

參考文獻(xiàn)：

[1] Gale D. A theorem on flows in networks[J]. Pacific Journal of Mathematics,1957,(2):1073-1082.

[2] Ryser H J. Combinatorial properties of matrices of zeros and ones[J]. Canadian Journal of Mathematics, 1957, (9):371-377.

[3] Garg A, Goel A, Tripathi A. Constructive extensions of two results on graphic sequences[J]. Discrete Mathematics,2011,(17):2170-2174.

(責(zé)任編校：晴川)

Generalization of Characterization Theorem on Interval Bigraphic Sequences

GUO Jiyun, CAI Baiguang

(College of Information Science and Technology, Hainan University, Haikou Hainan 570228, China)

Abstract：Let Pm=p1,…,pm and Qn=q1,…,qn be two non-increasing sequences of nonnegative integers. The pair (Pm,Qn) is said to be bigraphic if there is a simple X,Y-bigraph G such that the vertices of X have degrees p1,…,pm and the vertices of Y have degrees q1,…,qn. In this case,G is called a realization of (Pm,Qn).The pair (Pm,Qn) is said to be t-bigraphic if it is bigraphic and no two vertices from different partite sets are joined by more than t edges. In this case, the realization of (Pm,Qn)is called a t-bigraph. Gale and Ryser presented a classical characterization theorem on bigraphic sequences. Garg et al.considered interval bigraphic sequences, and gave a corresponding characterization theorem.In this paper, we generalize Garg’s characterization theorem from 1-graph to t-graph.

Key Words：bigraphic sequence; interval bigraphic sequence;t-bigraphic sequence

中圖分類號(hào):O157.5

文獻(xiàn)標(biāo)識(shí)碼：A

文章編號(hào)：1008-4681(2016)02-0004-02

作者簡(jiǎn)介：郭紀(jì)云(1984— ),女,山東菏澤人,海南大學(xué)信息科學(xué)技術(shù)學(xué)院講師,碩士.研究方向:圖論及其應(yīng)用.

基金項(xiàng)目：海南省自然科學(xué)基金資助項(xiàng)目(批準(zhǔn)號(hào)：20151004, 114001).

收稿日期：2016-03-07