一個具有相互作用非線性項的分數階微分方程組的爆破解

李　萍，　舒　級,　張　佳，　廖　歐

(四川師范大學 數學與軟件科學學院, 四川 成都 610066)

?

一個具有相互作用非線性項的分數階微分方程組的爆破解

李萍，舒級*,張佳，廖歐

(四川師范大學 數學與軟件科學學院, 四川 成都 610066)

摘要：討論一類具有相互作用非線性項的分數階微分方程組的爆破解.首先給出分數階導數的形式，并得到分數階微分方程組局部解的存在性，其次由H?lder不等式估計方程組的解，得到其在有限時間內的爆破解，并給出其解爆破時間上界的估計.

關鍵詞：分數階微分方程； 爆破解； 上界； H?lder不等式

分數階微分方程指的是含有分數階導數或者分數階積分的方程.目前,分數階導數和分數階積分在物理、生物、化學等多個學科有著廣泛的應用，如具有混沌動力行為的動力系統、擬混沌動力系統、復雜物質或者多孔介質的動力學、具有記憶的隨機游走等[1].本文考慮下面非線性時間α階微分方程組

初始條件：u(0)=u0,v(0)=v0,其中,p>1、q>1、u0>0、v0>0均是常數，Dα、Dβ是Caputo分數階導算子，0<α<1,0<β<1,A(t)、B(t)是連續函數.

研究上述具有相互作用非線性項的分數階微分方程組的爆破解.隨著科學技術的發展，非線性方程的研究內容日趨豐富，尤其是在流體力學、非線性光學、經典場論、量子力學等領域已有大量研究[2-4].近幾年來，分數階偏微分方程在材料力學、生物學、等離子體物理學、金融學、化學等更多領域中被提出，并蓬勃地開展著研究，其中包括分數階非線性Schr?dinger方程、分數階Navier-Stokes方程以及分數階Ginzburg-Landau方程等[5-18].這些研究都有明確的物理背景，開辟了一個嶄新的研究領域.早在17世紀末，一些數學家如L’Hpital、Leibniz、Euler等就開始思考如何定義分數階導數.19世紀70年代，Riemann、Liouville將Cauchy積分公式推廣，得到函數的分數階導數的定義[1].本文將通過H?lder不等式得到方程組(1)在有限時間內的爆破解.首先給出分數階微積分的一些基本定義,然后再給出方程組(1)的局部解存在性，最后得出主要結果并加以證明.

1預備知識

下面首先給出分數階微積分的基本定義，參見文獻[1,5].

定義 1.1設f在Jo=(0,∞)上分段連續，并且在J=(0,∞)的任意有限子區間上可積，對任意的t>0以及使得Reα>0的任意的復變量α,函數f的α階R-L分數階積分定義為

(2)

其中規定D0f(x)=f(x).

α階的Riemann-Liouville分數階積分算子性質:若α,β≤0,則有

(3)

定義 1.2Riemann-Liouville分數階導算子Dα定義如下

(4)

其中,m-1<α0.

(5)

其中m-1<α≤m,m∈N,x>0.

接下來給出方程組(1)的局部解存在性，證明方法參見文獻[5].

假設存在常數M>0，使得|A(t)|≤M,|B(t)|≤M,0≤t≤T,并且滿足Lipschitz條件：

考慮積分方程組

定理 1.1[5]設x(t),y(t)，t∈[0,T]是積分方程組(6)的連續解，令

(7)

那么(u,v)就是滿足初始條件u(0)=u0,v(0)=v0的方程組(1)的解.

2方程組的爆破解

在本節將給出方程組(1)在有限時間內的爆破解和爆破時間的一個上界.

定理 2.1如果u0>0,v0>0,p>1,q>1,A(t)>0,B(t)>0是連續函數，并且滿足Lipschitz條件：

則方程組(1)的解在有限時間內爆破，并給出了其解爆破時間上界的一個估計.

證明(反證法)假設(u,v)是方程組(1)的全局解.設

(8)

滿足

(9)

(10)

其中

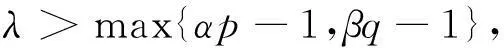
因為Riemann-Liouville分數階導算子在[0,T]上積分滿足公式(參見文獻[1])

(11)

則在方程組(1)兩側同時乘以φ(t),再在區間[0,T]上對t積分有

(12)

可以得到

(13)

同理

(14)

因為A(t)>0,B(t)>0是連續函數，則存在常數L>0使得A(t)≤L,B(t)≤L,t∈[0,T],由H?lder不等式可得

(15)

同理可得

令

(17)

于是得到

(18)

同理可得

(19)

(20)

代入(18)式中得

(21)

其中

(22)

代入(20)式可得

(23)

(24)

所以

(25)

其中

當T→∞時，在(25)式中可得到v0≤0,這與已知v0>0矛盾，故假設不成立，方程組(1)存在有限時間的爆破解.

下面對爆破時間進行估計，將(21)式代入(25)式中有

(26)

其中

(27)

同理對u0進行估計

(28)

(29)

由于

(30)

所以

(31)

當T→∞時，在(31)式中可得到u0≤0,這與已知u0>0矛盾，故假設不成立,方程組(8)有有限時間的爆破解.

下面對爆破時間進行估計，將(18)和(20)式代入(31)式中有

u0≤

(32)

其中

因此，得到爆破解的時間上界為

參考文獻

[1] 郭柏靈,蒲學科,黃鳳輝. 分數階偏微分方程及其數值解[M]. 北京:科學出版社,2011.

[2] 舒級,成和平. 一類帶外部磁場的非線性Schr?dinger方程解的爆破和整體存在[J]. 四川師范大學學報(自然科學版),2006，29(5)：512-515.

[3] 鮑杰，舒級. 高階廣義2D Ginzburg-landau 方程的隨機吸引子[J]. 四川師范大學學報(自然科學版)，2014，37(3)：298-306.

[4] 曾群香，黃欣，舒級，等. Wick-型混合隨機Kdv方程的精確解[J]. 四川師范大學學報(自然科學版)，2015,38(1)：27-33.

[5] 代群，李輝來. 對一個非線性分數階微分方程組的爆破解的研究[J]. 中國科學:數學,2012,42(12)：1205-1212.

[6] HE J H． Some applications of nonlinear fractional differential equations and their approximations[J]． Bull Sci Technol，1999，15(2):86-90．

[7] HE J H． Approximate analytical solution for seepage flow with fractional derivative in porous media[J]． Comput Methods Appl Mech Eng,1998,167(1/2):57-68．

[8] CARPINTERI A, MAINARDI F． Fractals and Fractional Calculus in Continuum Mechanics[M]． Berlin:Springer-Verlag，1997．

[9] ZHANG W． Fractional calculus approach to dynamic problems of viscoelastic materials [J]． JSME Inter J，1999，42C(4):825-837.

[10] GENZER J． Further results on the modelling of complex fractals in finance，scaling observation and optimal portfolio selection[J]． Systems Analysis Modelling Simulation，2001，42(10):1483-1499．

[11] HU Y Z, OKSENDAL B． Fractional white noise calculus and applications to finance[J]． Infinite Dim Anal Quantum Probab Related Topics,2003,6(1):1-32．

[12] JUMARIE G． New stochasti fractional models for malthusian growth，the poissonian birth process and optimal management of populations[J]． Math Comput Mod,2006,44(3/4):231-254．

[13] GORENFLO R, MAINARDI F． Fractional calculus: Integral and differential equations of fractional order [C]//Fractals and Fractional Calculus in Continuum Mechanics．Vienna:Springer-Verlag，1997:223-276．

[14] PODLUBNY I． Fractional Differential Equation[M]． New York:Academic Press,1999．

[15] PODLUBNY I． Geometric and physical interpretation of fractional integratiation and fractional differential[J]． Fract Calculus Appl Anal，2002，5:367-386．

[16] LANGLANDS T A M, HENRY B I, WEARNE S L． Fractional cable equation models for anomalous electrodiffusion in nerve cells: infinite domain solutions[J]． J Math Biol，2009，59(6):761-808．

[17] JUMARIE G． Laplace’s transform of fractional order via the Mittag-Leffler function and modified Riemann-Liouville derivative[J]． Appl Math Lett，2009，22(11):1659-1664．

[18] KILBAS A A, SRIVASTAVA H M, TRUJILLO J J. Theory and Applications of Fractional Differential Equations[M]．Amsterdam:Elsevier,2006.

2010 MSC：35B44; 35R11; 34A08; 34K37

(編輯陶志寧)

Blowing-up Solutions for a Nonlinear System of Fractional Differential Equations with Interaction Nonlinearity

LI Ping,SHU Ji,ZHANG Jia,LIAO Ou

(CollegeofMathematicsandSoftwareScience,SichuanNormalUniversity,Chengdu610066,Sichuan)

Abstract：In this paper, we discuss the blow-up solutions of a nonlinear system of fractional differential equations. Firstly we give the form of fractional derivatives and get the local existence of solutions to the system of the integral equations. Secondly we obtain the blow-up solutions to the fractional differential equations in a finite time by using H?lder’s inequality， and the upper bound of blowing-up time．

Key words：fractional differential equation; blowing-up solution; upper bound; H?lder inequality

doi:10.3969/j.issn.1001-8395.2016.01.003

中圖分類號：O177.92

文獻標志碼：A

文章編號：1001-8395(2016)01-0015-05

*通信作者簡介：舒級(1977—),男,副教授,主要從事隨機動力系統、偏微分方程的研究,E-mail:shuji2008@hotmail.com

基金項目：國家自然科學基金(11371267)和四川省教育廳重點科研基金(14ZA0031)

收稿日期:2014-07-01