基于非線性收斂因子的Terminal滑模制導律設計

劉明雍, 張小件, 李洋

(西北工業大學 航海學院,陜西 西安　710072)

?

基于非線性收斂因子的Terminal滑模制導律設計

劉明雍, 張小件, 李洋

(西北工業大學 航海學院,陜西 西安710072)

摘要：水下動能武器在末端時刻攻擊目標具有作戰范圍小,時間短的特性。傳統滑模變結構制導律通常選取線性滑動平面,收斂速度慢,對收斂時間沒有約束,不能滿足系統快速收斂到平衡狀態。針對這一問題,提出一種改進的Terminal滑模變結構控制方法,通過引入非線性因子,使系統跟蹤誤差快速收斂到零,保證系統以期望的有限時間收斂到平衡狀態。采用Terminal滑模面結合指數趨近律設計有限時間快速收斂制導律,該制導律即能滿足系統快速性收斂要求,又能離線計算收斂時間。理論分析表明:所設計的制導律滿足系統穩定性要求,并仿真驗證了其快速收斂的有效性,較傳統變結構制導方法收斂速度更快,具有更強的魯棒性。

關鍵詞：Terminal滑模面；變結構控制；制導律；動能武器

當今乃至未來的海戰是一個水下武器對抗的時代,為了提高自身的安全性,針對外來的攻擊,各國海軍競相發展出了攻擊或攔截外來武器的動能武器[1]。水下動能武器具有體積小、速度高、攻擊距離短、制導系統反應時間短等特點,要求制導武器系統要有快速的系統收斂及直接命中目標的特性。

當制導武器攻擊目標時,不僅希望系統能夠快速收斂到平衡狀態,以便有足夠的時間應對目標機動;同時希望獲得較小的脫靶量,以直接命中目標,達到毀傷的效果。因此,本文在設計制導律的過程中主要考慮兩方面的因素:有限時間收斂和脫靶量為零。有限時間收斂能夠保證系統快速響應目標機動;脫靶量為零能夠保證直接命中目標,獲得最大的毀傷效果。

有限時間收斂即制導系統在有限時間內達到平衡狀態作為制導武器實現攻擊目標的一個重要研究方面。以往學者對有限時間收斂做了不少的研究工作。其中,文獻[2]提出了一種時間收斂的滑模變結構制導律,該制導律能夠保證系統在攻擊目標末端命中時刻收斂到平衡狀態。文獻[3]對二階非線性不確定系統設計滑模面,保證了輸出跟蹤誤差有限時間收斂到零。文獻[4]針對不確定非線性系統提出了動態滑模控制,保證了系統在一定時間內收斂。以上文獻[3-4]都需要跟蹤誤差模型具有二階甚至高階連續可導,且有限時間“較長”。另外,根據滑模面的收斂特性,有學者們提出了在滑模面中引入非線性項以提高系統的收斂特性,縮短收斂時間[5]。文獻[6]從碰撞時間入手,提出基于非線性理論設計的滿足碰撞時間的制導律,該制導律不同于以遞歸和數值解的方法求解碰撞時間,而是通過反饋閉環系統求出精確的碰撞時間,對于具有延遲的制導與控制系統達到了較好的估計、補償效果。文獻[7]綜合考慮自動駕駛儀動態特性及系統的不確定性,提出一種時間收斂的制導律。該制導律通過在有限的時間內估計目標機動信息,然后根據估計獲得的目標機動信息設計滿足時間收斂的滑模變結構制導律。一定程度上補償了由自動駕駛儀的動態特性和系統不確定性帶來的誤差。文獻[8]通過改變Terminal滑模面的非線性項,避免了奇異點的出現。

在本文中,從系統快速收斂這一角度提出了一種基于非線性收斂因子的Terminal 滑模控制制導律,通過引入非線性因子,改變滑模面參數,保證制導系統能夠在期望的有限時間內以任意初始狀態收

斂到平衡狀態,并且收斂時間能夠通過滑模參數離線計算出來。結合本文的滑模面推導出了動能武器末端制導律,通過仿真分析該制導律能夠以期望的有限時間使制導系統達到平衡狀態,從而直接命中目標,而且對外界干擾具有很強魯棒性。

1問題描述

水下動能武器在攻擊或攔截目標時,由于主要是靠動能毀傷,要求動能武器能直接命中目標。而在攻擊目標的過程中,目標可能存在機動,要求動能武器具有應對目標機動的快速收斂方法。即主要從脫靶量和收斂時間對本文制導律進行分析設計。

考慮到彈目相對運動關系。彈目相對運動方程可以解耦為俯仰平面和偏航平面的2個分量運動,本文只考慮俯仰平面內的運動,如圖1所示。

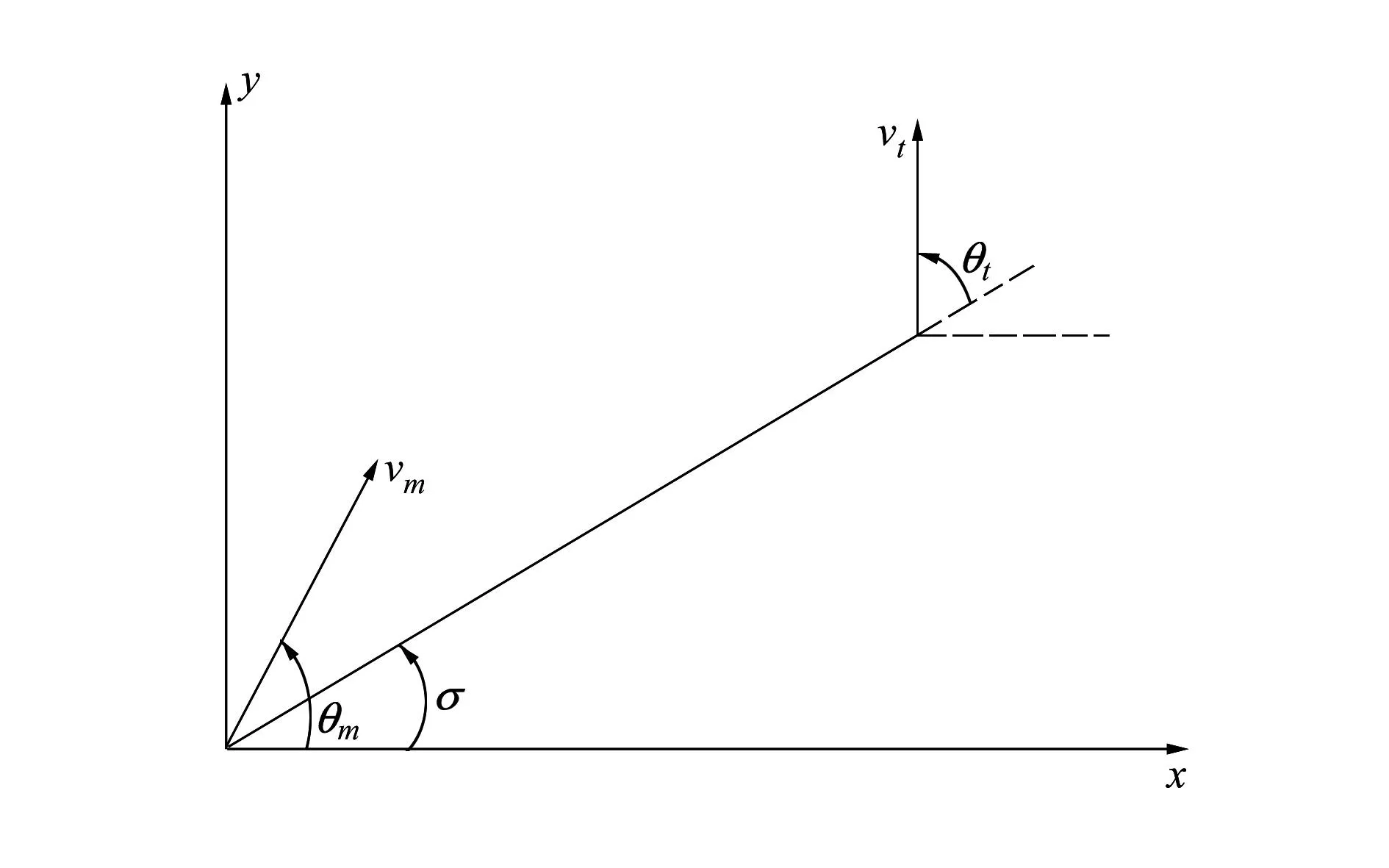
圖1　彈目相對運動幾何關系圖

假設動能武器速度和目標速度均為常量,分別為vm、vt,且動能武器速度大于目標速度。其中θm、θt分別為動能武器與目標的航向角;σ為視線角,即二維平面內攔截器與視線角之間的連線與水平方向上的夾角,其變化率為零表明動能武器能夠擊中目標。

根據彈目相對幾何關系可知

(1)

(2)

(3)

式中：r(t)為動能武器與目標相對距離,u=aA(t)為動能武器控制輸入,即本文要設計的制導律;at為目標過載,這里可視為干擾。

(4)

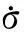
2有限時間收斂

2.1有限時間收斂概念

對于非線性系統:

(5)

式中，f:U0×R→Rn在U0×R上連續,且U0為原點x=0的一個開鄰域,f(0,t)=0。系統的平衡點x=0有限時間收斂,對于任意給定的初始時刻t0所對應的初始狀態x(t0)=x0∈U,存在一個依賴于x0的時間T≥t0,使得系統方程以x0為初始狀態的解x(t)=φ(t:t0,x0)有定義,并且:

(6)

當時間t∈[t0,T)時,φ(t:t0,x0)∈U/0。此系統的平衡點x=0有限時間穩定,是指它是Lyapunov穩定和在原點的一個鄰域U∈U0內有限時間收斂。如果U=Rn,那么系統在全局范圍內有限時間收斂[9]。

2.2Terminal滑模面

傳統滑模面收斂特性主要取決于趨近律的選取,且沒有時間約束,并存在很大抖動,不能滿足系統快速性收斂的要求,同時抖動給系統的穩定性帶來一定影響。為此,基于傳統滑模面原理,有學者在滑模面種引入非線性項,以改變系統的收斂特性[10]:

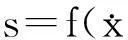
若定義滑模面s1

(7)

其收斂時間

(8)

滑模面s2

(9)

其收斂時間

(10)

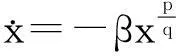
2.3改進的滑模面

為了證明改進的滑模面的收斂速度優于傳統Terminal滑模面,首先介紹以下定理:

定理1[10]對于非線性系統

(11)

式中。φ(x)在C(-∞,∞)有定義,并滿足φ(x)>-β,且q>p,都為奇整數。則系統(11)是漸進穩定的,且對于任意初始狀態x(t0)≠0,系統都能在有限時間內達到平衡點。

穩定性證明

令

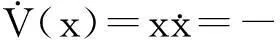
命題1 假設φ(x)在c(-∞,∞)有定義,并滿足φ(x)≥0。當|x|≥1時,如果φ(x)≥

α|x|(q-p)(1+ε)/q(其中q>p>0,且都為奇整數; α,β,ε>0)。對于任意初始狀態x(t0)≠0,系統(11)有限時間穩定,且對于任意初始狀態x(t0)收斂時間是有界的。

證明從定理1可以明顯得出系統(7)是穩定的,下面主要考慮收斂時間。

由φ(x)≥α|x|(q-p)(1+ε)/q可知

(12)

令x=yq/(q-p),則

(13)

定義

當|x|>1時

(14)

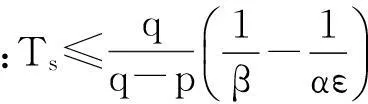
證畢,即系統有限時間收斂。

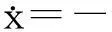
3制導律設計

根據前文分析,選取滑模面

(15)

式中，m>n>0,q>p>0,且都為奇整數;α,β,γ>0。

取趨近律:

(16)

式中，k1,k2>0。

對(15)式進行微分得:

(17)

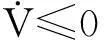
結合(4)式、(16)式及(17)式可得制導律表達式

(k1s+k2sgn(s))r+at

(18)

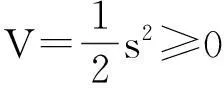
4仿真及結果分析

本節將比較本文所設計的快速Terminal滑模變結構制導律與傳統滑模變結構制導律。從目標靜止和目標機動2種情況進行分析。

4.1目標靜止

假設動能武器以50 m/s的速度航行攻擊目標,初始位置M(x0,y0)=M(0,0),初始航向角為0°;目標初始位置 T(x0,y0)=T(300,400)。仿真中選擇合適的參數:m=5,n=3,q=3,p=1,α=2,β=0.03,γ=0.1,k1=k2=0.01,仿真步長取0.01s。仿真結果如圖2～圖4所示(其中實線表示基于Terminal滑模變結構制導律仿真結果,虛線表示基于傳統滑模面變結構制導律仿真結果)。

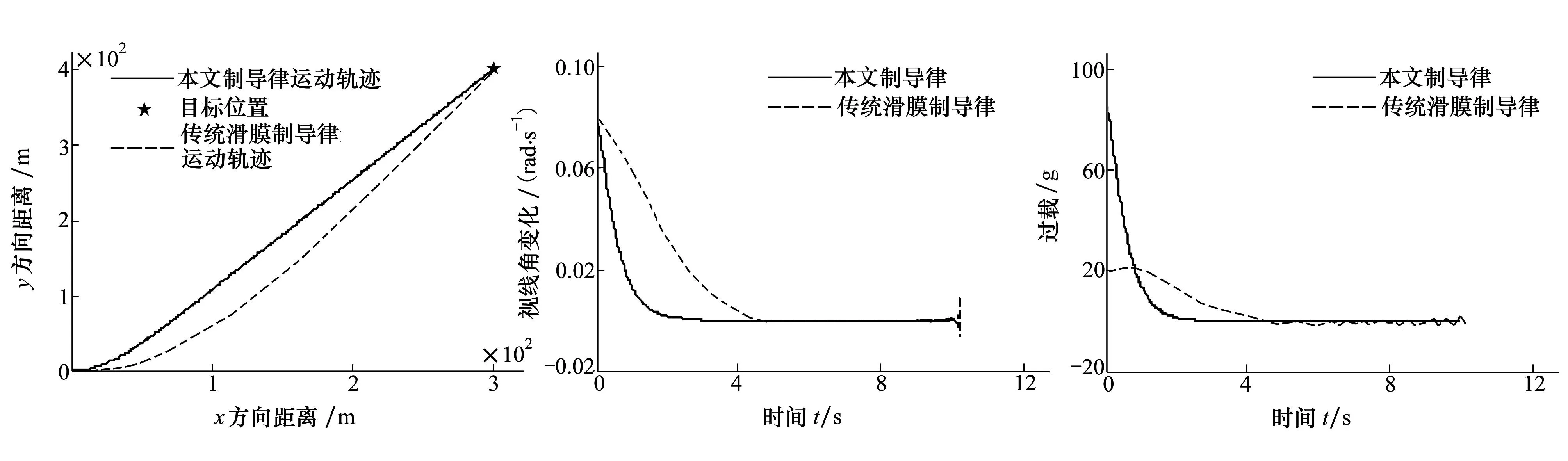
圖2　動能武器運動軌跡　　　　　　　圖3　視線角變化率曲線圖4　動能武器過載隨時間變化曲線

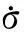
4.2目標機動

假設動能武器以50 m/s的速度航行,初始位置M(x0,y0)=M(0,0),初始航向角為0°;目標航行速度30 m/s,初始位置T(x0,y0)=T(300,400),初始航向角為180°,目標做10*rand(1)隨機機動。仿真中各參數同目標靜止時選取同樣的數值,仿真步長取0.01 s。仿真結果如圖5～圖7所示。

圖5為過載隨時間變化曲線,雖然目標處于隨機機動狀態,動能武器在制導律(18)的作用下相應進行調整軌跡,以保證命中目標,但是動能武器過載基本穩定在某一范圍內;圖7對應的是視線角變化率隨時間變化曲線,從圖5和圖7中可以看出,攔截器在2 s左右達到了收斂狀態,較傳統滑模控制具有更快的收斂速度,且抖動更小。從圖6運動軌跡可以看出,本文制導律能隨目標機動做出快速的響應,為動能武器在后期攔截目標的過程中提供充足的應變時間。能夠有效攔截目標。

圖5　動能武器過載變化曲線　　　　　　　圖6　運動軌跡圖7　視線角變化率隨時間變化曲線

5結論

參考文獻：

[1]嚴衛生, 任章, 徐德民, 等. 迎面攔截變結構導引律及其應用研究[J]. 西北工業大學學報, 2000, 18(4): 616-620

Yan Weisheng, Ren Zhang, Xu Demin, et al. A Head-on Impact Variable Structure Guidance Law[J]. Journal of Northwestern Polytechnical University, 2000, 18(4): 616-620 (in Chinese)

[2]Zhang Y, Sun M, Chen Z. Finite-Time Convergent Guidance Law with Impact Angle Constraint Based on Sliding-Mode Control[J]. Nonlinear Dynamics, 2012, 70(1): 619-625

[3]Kaiyu Z, Hongye S U, Keqin Z, et al. Adaptive Terminal Sliding Mode Control for High-Order Nonlinear Dynamic Systems[J]. Journal of Zhejiang University Science, 2013, 4(1): 58-63

[4]Liu J, Sun F. A Novel Dynamic Terminal Sliding Mode Control of Uncertain Nonlinear Systems[J]. Journal of Control Theory and Applications, 2007, 5(2): 189-193

[5]Slotine J J E, Li W. Applied Nonlinear Control[M]. Englewood Cliffs, NJ: Prentice-hall, 1991

[6]Saleem A, Ratnoo A. A Nonlinear Guidance Law for Impact Time Control[C]∥American Control Conference (ACC), 2015: 651-656

[7]Li G L, Yan H, Ji H B. A Guidance Law with Finite Time Convergence Considering Autopilot Dynamics and Uncertainties[J]. International Journal of Control, Automation and Systems, 2014, 12(5): 1011-1017

[8]湯一華, 陳士櫓, 徐敏, 等. 基于Terminal滑模的動能攔截器末制導律研究[J]. 空軍工程大學學報: 自然科學版, 2007, 8(2): 22-25

Tang Yihua, Chen Shilu, Xu Min, et al. Terminal Guidance Law of Kinetic Interceptor Based on Terminal Sliding Mode[J]. Journal of Air Force Engineering Uuniversity: Natural Science Edition, 2007, 8(2): 22-25 (in Chinese)

[9]Zhang Y, Sun M, Chen Z. Finite-Time Convergent Guidance Law with Impact Angle Constraint Based on Sliding-Mode Control[J]. Nonlinear Dynamics, 2012, 70(1): 619-625

[10] Tie L, Cai K Y. A General Form and Improvement of Fast Terminal Sliding Mode[C]∥Intelligent Control and Automation (WCICA), 2010 8th World Congress on IEEE, 2010: 2496-2501

Nonlinear Convergence Factor Terminal Mode Based Guidance Law Design

Liu Mingyong, Zhang Xiaojian, Li Yang

(College of Marine Science and Technology, Northwestern Polytechnical University, Xi′an 710072, China)

Abstract:Kinetic weapon attack targets underwater with small range operations, short time features at the end of the time. Traditional linear sliding mode control guidance law can not meet the system in a finite time fast convergence to equilibrium requirements, that can not ensure attacking the target effectively. To solve the problem, this paper proposes an improved Terminal Sliding Mode Control method, guarantee system convergence to equilibrium state in finite time, by introducing nonlinear factor, make the system tracking error converge to zero quickly. By combining with exponential reaching law Terminal sliding mode surface design limited time fast convergent guidance law. The guidance law can ensure that the system convergence to equilibrium fast and calculate convergence time off-line. Theoretical analysis, the designed guidance law can meet the requirements of the system′s stability, and its effectiveness was verified through simulation, and its convergence time is faster than traditional variable structure guidance law, has stronger robustness.

Keywords:Calculations, computer simulation, convergence of numerical methods, design, electronic guidance systems, Lyapunov methods, robustness(control systems), sliding mode control,stability,trajectories, variable structure control; guidance law, Kinetic weapons, terminal sliding mode

中圖分類號：V448.234

文獻標志碼：A

文章編號:1000-2758(2016)01-0047-06

作者簡介：劉明雍(1971—)，西北工業大學教授、博士生導師，主要從事航行器制導與控制研究。

基金項目：國家自然科學基金(51109179、51379176、61473233)資助

收稿日期：2015-10-09