基于兩端點區域分布的線裁剪新算法

任洪海(大連交通大學軟件學院，遼寧大連116052)*

基于兩端點區域分布的線裁剪新算法

任洪海
(大連交通大學軟件學院，遼寧大連116052)*

在確定線段完全在窗口內或某邊界外初始判斷后將兩端點的區域分布分成6種情況進行處理.除可直接確定相交關系的情況外，一般過指定頂點在窗外作與對應邊呈45度的輔助邊界進一步排除完全在窗外的線段，再通過線段與指定邊界相交測試確定線段與窗口的位置關系.該方法可以加快線段與窗口的求交進程，有效減少不必要的求交運算和輔助操作，顯著提高裁剪效率.

計算機應用;線裁剪;兩端點區域分布

0 引言

線裁剪作為計算機圖形學基礎理論的重要內容之一，經典的算法主要有以區域碼為代表的Cohen-Sutherland算法、中點分割算法、參數化的梁-Barsky算法以及Nicholl-Lee-Nicholl算法［1］.文獻［2］將線段兩端點獨立考慮，并將其區域分布分成邊域和角域兩種基本情況，并根據線段相交對應邊界的情況確定線段與窗口的相交關系.近年來也有一些算法將原窗口擴大并旋轉45°形成新窗口用來舍棄不與窗口相交的線段［3-4］，但存在冗余邊界測試.

本文通過線段完全在窗口之內或某邊界之外的初始判斷后，將線段兩端點相對于窗口邊界所劃分區域的分布分成5種情況進行處理.在必要情況下過指定窗口頂點作輔助邊界排除不與窗口相交的線段，再根據線段相交于指定邊界的范圍快速確定線段與窗口的相交情況.減少不必要的輔助操作和求交運算，顯著提高裁剪效率.

1 區域對應關系及輔助邊界

1.1窗口邊界劃分區域及對應關系

如圖1所示，作為矩形裁剪窗口的四條邊分別標記為L邊、R邊、B邊、T邊.將每條邊延長成直線形成對應邊界，分別為L邊界( x = xwmin)、R邊界( x = xwmax)、B邊界( y = ywmin)、T邊界( y = ywmax).四條邊界將平面分成九個區域，根據區域位置及符號標識，區域對應關系如下:

邊區與一條邊界相對應;而角區和兩條垂直相交的邊界相對應.例如，T邊區與T邊界相對應; LB角區與L邊界、B邊界相對應.窗口頂點是由兩條邊界垂直相交而成，一條邊界可稱另一邊界對應頂點相關邊界.例如，L邊界與B邊界相交而成頂點VLB，L邊界稱B邊界為頂點VLB相關邊界.根據邊界所屬，一角區與一頂點相對應，兩斜對邊區與一頂點相對應.例如，LB角區對應頂點VLB，R邊區與T邊區對應頂點VRT.

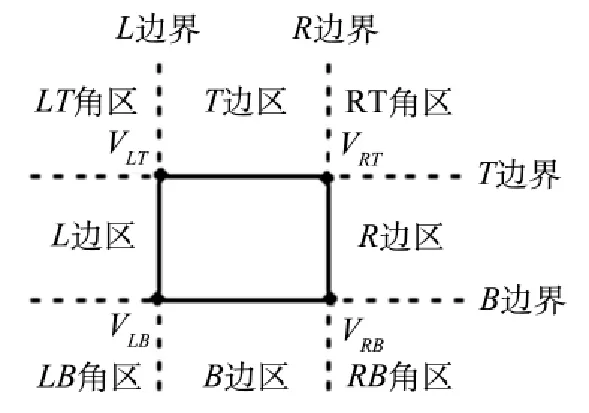
圖1 裁剪窗口邊界區域劃分

對應邊界相平行的兩邊區稱為對邊區.例如，T邊區和B邊區為對邊區，L邊區和R邊區為對邊區.對應邊界相垂直的兩邊區稱為斜邊區.例如，T邊區是L邊區的斜邊區，T邊區是R邊區的斜邊區.

不同時在任何邊界之外的角區和邊區稱為斜對關系，每個邊區都有兩個斜對角區.例如，T邊區有兩個斜對角區，即LB角區和RB角區.

不同時在任何邊界之外的兩角區為對角區.四個角區中，LT角區和RB角區為對角區，RT角區和LB角區為對角區.

1.2輔助邊界

在窗口外分別過指定頂點引與對應邊界成45°的直線，定義為輔助邊界.判斷線段端點在此類輔助邊界之外的條件為:

端點在過頂點VLT所引輔助邊界之外的條件為: y－x + xwmin＞ywmax

端點在過頂點VLB所引輔助邊界之外的條件為: x + y－ywmin＜xwmin

端點在過頂點VRB所引輔助邊界之外的條件為: y－x + xwmax＜ywmin

端點在過頂點VRT所引輔助邊界之外的條件為: x + y－ywmax＞xwmin

如果線段兩端點同時在過任意一條此類邊界之外，則線段在窗口之外，裁剪掉該線段.

本文根據線段兩端點的區域分布完全可確定過哪個頂點作輔助邊界進行測試，而不必同時檢測四個輔助邊界.

2 算法實現過程

通過線段兩端點坐標與窗口四條邊界坐標相比較確定兩端點所在區域，并進行如下初始判斷:

如果兩端點都在四條邊界之內，則線段在窗口之內，保留該線段;

如果兩端點都在四條邊界中任意一條的外側，則線段在窗口之外，裁剪該線段.

通過兩步初始判斷后，所剩線段兩端點的區域分布情況完全可概括成6類情況:①一端點在窗口內另一端點在邊區;②一端點在窗口內另一端點在角區;③一端點在邊區另一端點在其對邊區;④一端點在邊區另一端點在其斜對邊區;⑤一端點在邊區另一端點在其斜對角區;⑥一端點在角區另一端點在其對角區.

針對6種情況，分別具體處理如下:

對于情況①:可得線段只與邊區對應邊相交，窗口內端點到交點間線段為裁剪結果(如圖2中線段a).

對于情況②:可得線段一定與兩角區對應邊之一相交(如圖3中線段a和線段b).求線段與任一對應邊界的交點，判斷是否在其對應窗口邊上:

如果交點在其對應窗口邊上，則內端點到交點間線段為裁剪結果.

否則，線段一定與另一對應窗口邊相交.求其交點，內端點到交點間線段為裁剪結果.

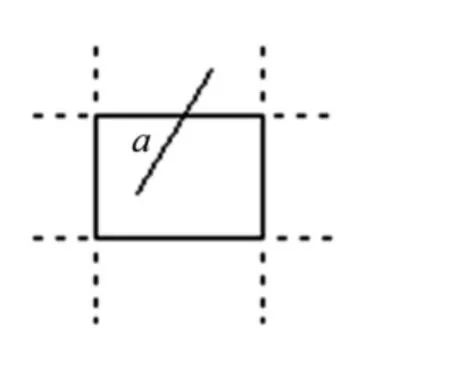
圖2 窗口內-邊區情況

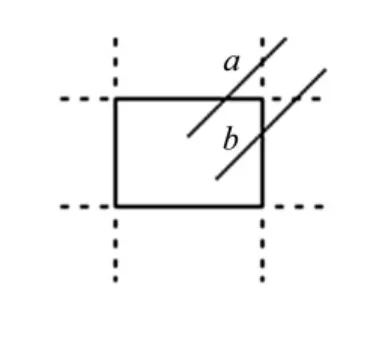
圖3 窗口內-角區情況

對于情況③:可得線段分別與兩對應邊相交，交點間線段為裁剪結果(如圖4中線段a ).

對于情況④:可得線段或不與窗口相交或同時與兩邊區的對應邊相交.過兩邊區對應邊界相交而成的頂點作輔助邊界，排除兩端點都在此輔助邊界之外的線段(如圖5中線段a ) ;對于輔助邊界無法排除的線段，指定兩邊區對應邊界任意一個，判斷線段是否相交在對應邊上:

如果交點在對應邊上，則線段一定與另一邊也相交.求在另一邊上的交點，交點間線段為裁剪結果(如圖5中線段c和線段d ).

否則，線段不與窗口相交(如圖5中線段b ).

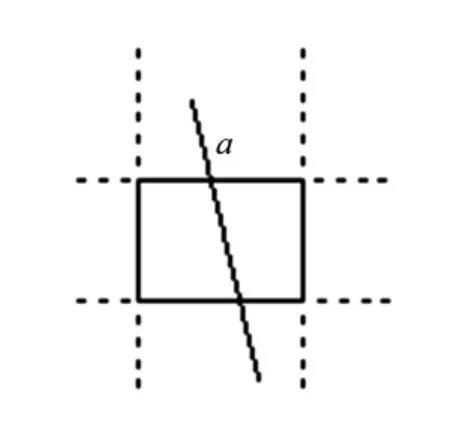
圖4 邊區-對邊區情況

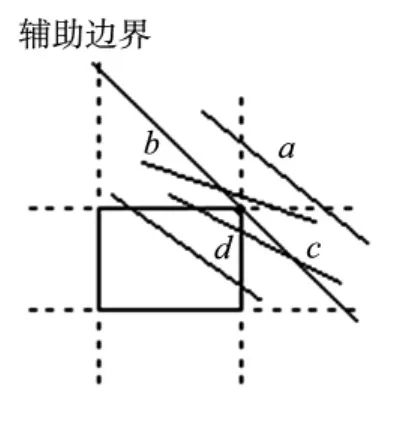
圖5 邊區-斜邊區情況

對于情況⑤:線段與窗口的位置關系有三種:①線段不與窗口相交;②線段與邊區對應邊及其垂直的角區對應邊相交;③線段與邊區對應邊及其平行的角區對應邊相交.

角區的兩個對應邊界中，一個與其斜對邊區對應邊界平行，另一個與其斜對邊區對應邊界垂直相交.取與斜對邊區對應邊界垂直相交的角區對應邊界為指定邊界，過邊區對應邊界與指定邊界相交而成的頂點作輔助邊界，排除兩端點都在此輔助邊界之外的線段后，判斷線段與指定邊界的相交范圍完全可確定線段與窗口相交關系.如圖6所示.

( 1)如果線段相交指定邊界于邊區對應邊界之外，則線段不與窗口相交;

( 2)如果線段相交指定邊界于對應窗口邊上，則線段同時與邊區對應邊相交，兩交點間線段為裁剪結果;

( 3)否則，線段與邊區對應邊及其對邊相交，兩交點間線段為裁剪結果.

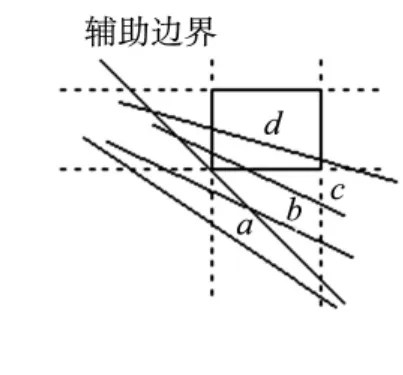
圖6 邊區-斜對角區情況

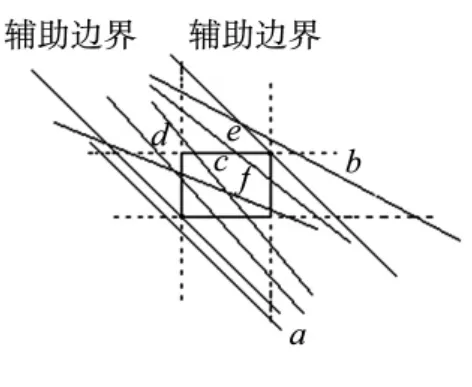
圖7 角區-對角區情況

對于情況⑥:此時，線段一定不同時與端點所在角區兩對應邊相交.因此，線段與窗口的位置關系有五種:①線段不與窗口相交;②相交于窗口兩垂直方向對邊;③相交于窗口兩水平方向對邊;④一個非端點所在角區兩對應邊;⑤另一個非端點所在角區兩對應邊.如圖7所示.

便于描述，將端點所在角區對應頂點稱為本頂點，而非端點所在角區對應頂點稱為基頂點.過兩基頂點分別作輔助邊界，排除兩端點同時在任意輔助邊界之外的線段后.取任意兩平行邊界為兩指定邊界，通過判斷線段與兩指定邊界的相交情況可確定線段與窗口的相交關系:

( 1)如果線段相交指定邊界于其基頂點相關邊界之外，則線段不與窗口相交;

( 2)如果線段相交指定邊界對應邊上且相交另一平行邊界于其本頂點相關邊界之外，則線段與指定邊界對應邊及其基頂點相關邊界對應邊相交，交點間線段為裁剪結果;

( 3)如果線段相交兩指定邊界對應邊上，兩對應邊上交點間線段為裁剪結果;

( 4)如果線段同時相交兩指定邊界于本頂點相關邊界之外，線段同時與兩非指定邊界對應邊相交，交點間線段為裁剪結果.

3 算法分析與比較

本文根據端點的區域分布通過指定頂點在窗口之外作與對應邊呈45°的輔助邊界進一步排除不與窗口相交的線段，避免文獻［4］中應用45°旋轉窗口對應四條新邊界測試過程中不必要的邊界判斷.

通過線段與邊界的相交情況確定線段與窗口的相交關系是裁剪判斷的有效途徑.本文算法將線段兩端點區域分布分成6種可能情況:情況①和情況③直接可確定線段與窗口的相交邊，情況②、情況④和情況⑤通過判斷線段相交一條指定邊界范圍可完全確定相交情況，情況⑥通過線段相交兩條平行邊界范圍可完全確定相交情況，同時每個相交邊界測試過程中都可以排除對應情況下不與窗口相交的線段.

同Cohe-Sutherland算法與文獻［2］相比，本文算法能夠根據線段兩端點區域分布情況確定最佳相交檢測邊界，從而減少不必要的求交運算.例如排除圖6中線段b，Cohen-Sutherland算法邊界裁剪如果按照固定的左、右、下、上順序需要左、右兩邊界裁剪后在下邊界判斷中才能將其排除.而文獻［2］由于單獨考慮兩端點區域分布情況分別進行裁剪判斷，同樣增加了多余判斷與邊界求交.而本文算法在該邊區-斜對角區端點分布情況中確定下邊界為指定邊界，通過判斷線段與下邊界一次相交情況就可排除線段b.

在同等硬件條件下，應用C ++編程實現CS算法、ELC算法［2］及本文算法，三個裁剪算法裁剪400萬條隨機線段所需的時間分別為3.529，3.274和2.418 s，從所用時間可以看出新算法的裁剪效率都高于現有的兩個典型算法.

4 結論

本文在初始測試后將線段兩端點區域分布分成5種情況分別進行判斷并完成裁剪過程，只有在必要的情況，才通過指定頂點在窗口之外作與對應邊呈45°的輔助邊界進一步排除不與窗口相交的線段，并通過線段相交于指定邊界的范圍確定線段與窗口的相交關系.以最少的輔助操作和求交判斷確定線段與窗口的位置關系，明顯提高裁剪效率.

［1］DONALD HEARN，PAULINE BAKER M.Computer Graphics with OpenGL［M］.Third Edition，Upper Saddle River: Prentice Hall，2005: 315-340.

［2］汪灝泓，吳銳迅，蔡士杰.一種基于幾何變換的高效的線裁剪新算法［J］.軟件學報，1998，9( 10) : 728-733.

［3］陸國棟，吳煊暉.基于變窗口過濾技術的線段裁剪中點分割算法［J］.計算機輔助設計與圖形學學報，2002，14( 6) : 513-517.

［4］朱亞臣，譚建榮，陸國棟，等.基于連續分區與串聯編碼的線段裁剪新算法［J］.中國圖象圖形學報，2007，12( 4) : 732-739.

A New Line Clipping Algorithm based on Region Distribution of Two Endpoints

REN Honghai
( Software Institute，Dalian Jiaotong University，Dalian 116052，China)

The region distribution of two endpoints is divided into six kinds of cases for processing after the initial testing to determine whether a line segment is completely inside the clipping window or outside some window boundary.Except for the case that the intersection relation is determined directly，the line segments outside window is further eliminated through the 45°auxiliary boundary passing the specified vertex，and the position of a line segment in relation to window is determined by the intersection test between a line segment and the specified boundary.The new algorithm can quickly calculate the intersections between a line segment and window，avoid the unnecessary intersection calculation and auxiliary operation，and further improve the clipping efficiency.

computer applications; line clipping;region distribution of two endpoints

A

1673-9590( 2016) 01-0105-04

2015-04-07

任洪海( 1977－)，男，講師，碩士，主要從事計算機圖形學教學與研究

E-mail: honghai_ren@126.com.