Bergman空間上k階斜Toeplitz算子的正規(guī)性及亞正規(guī)性

劉朝美，倪維丹(大連交通大學(xué)理學(xué)院，遼寧大連116028)*

Bergman空間上k階斜Toeplitz算子的正規(guī)性及亞正規(guī)性

劉朝美，倪維丹
(大連交通大學(xué)理學(xué)院，遼寧大連116028)*

對單位圓盤的Bergman空間上k階斜Toeplitz算子的正規(guī)性及亞正規(guī)性展開了研究，得到了帶有調(diào)和多項式符號的斜Toeplitz算子是正規(guī)的或亞正規(guī)的充要條件是其符號函數(shù)為零函數(shù).

Bergman空間;斜Toeplitz算子;正規(guī)性;亞正規(guī)性

0 引言

1996年，Mark引進了Hardy空間上斜Toeplitz算子的概念［1］，介紹了該類算子的背景，討論了該類算子的若干性質(zhì).他對該類算子的譜等性質(zhì)也展開了深入的討論［2-4］.Arora和Batra通過對斜Toeplitz算子定義的推廣，得到k階斜Toeplitz算子的概念，并對該類算子的性質(zhì)展開了一系列的討論［5-7］.

2004年，安恒斌和蹇人宜將斜Toeplitz算子的定義推廣到了單位圓盤的Bergman空間上，并對該類算子的有界性、緊性等性質(zhì)展開了研究［8］.既然可以將Hardy空間上的斜Toeplitz算子推廣為k階斜Toeplitz算子，那么人們自然會想到將Bergman空間上斜Toeplitz算子的概念進行推廣.2007年，Yang、Leng和Lu給出了Bergman空間上k階斜Toeplitz算子的概念，并對該類算子的譜、交換性等性質(zhì)展開了研究［9］.

此后，人們又對該類算子的交換性、有界性等性質(zhì)展開了研究，得到了一些結(jié)論［10-11］.

對函數(shù)空間上斜Toeplitz算子的性質(zhì)進行研究時，人們總是希望能夠?qū)⒃擃愃阕拥男再|(zhì)由其符號函數(shù)給出刻畫.本文對單位圓盤的Bergman空間上k階斜Toeplitz算子的性質(zhì)展開了研究，得到了帶有調(diào)和多項式符號的k階斜Toeplitz算子是正規(guī)的或亞正規(guī)的充要條件是其符號函數(shù)為零函數(shù).

1 基本概念

設(shè)C表示復(fù)平面，D = { z∈C: | z |＜1}為C上的單位開圓盤.用dA表示D的規(guī)范化面積測度，即.L2( D)表示在D上平方可積的可測函數(shù)全體構(gòu)成的Hilbert空間.設(shè)Bergman空間A2( D)為L2( D)中所有解析函數(shù)構(gòu)成的Hilbert空間，其一組正交基為{ zn: n∈Z+} ( Z+為非負整數(shù)集).設(shè)L∞( D)表示D上本性有界復(fù)可測函數(shù)全體構(gòu)成的Banach空間，其上的范數(shù)為

設(shè)k≥2是固定的正整數(shù)，定義在A2( D)上的算子Wk［9］為

且Wk是A2( D)上的有界線性算子，且共軛算子，其中n∈Z+.

設(shè)φ∈L∞( D)，Bergman空間A2( D)上以函數(shù)φ為符號的k階斜Toeplitz算子Bφ定義為Bφ= WkTφ，其中Tφ是A2( D)上以函數(shù)φ為符號的Toeplitz算子［9］.而且A2( D)上以本性有界函數(shù)為符號的k階斜Toeplitz算子均是有界線性算子［9］.

2 k階斜Toeplitz算子的正規(guī)性

本節(jié)將對Bergman空間上k階斜Toeplitz算子的正規(guī)性展開討論.利用函數(shù)的性質(zhì)可得以下引理.

引理1設(shè)k，s，t，q∈Z+，r = s + t + q＞0，若定義在實數(shù)域R上的函數(shù)h( x)和g( y)為

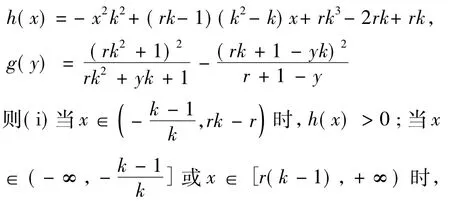
Hilbert空間上有界線性算子A是正規(guī)的，若AA*= A*A.現(xiàn)在討論Bergman空間上k階斜Toeplitz算子的正規(guī)性.

證明 若φ= 0，則顯然可得Bφ是正規(guī)的.若Bφ是正規(guī)的，則，從而對任意的非負整數(shù)n

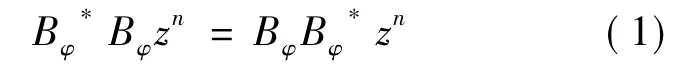
既然m1，m2均為非負整數(shù)，不妨設(shè)m1= sk + q1，m2= tk + q2，其中s，t，q1，q2∈Z+且q1＜k，q2＜k.由于式( 1)中n的任意性，不妨取n = ( s + t + q) k≥0，q = max{ q1，q2}，從而可得

故由式( 1)知可得

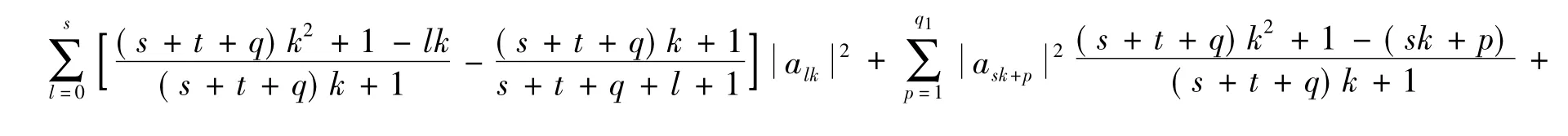
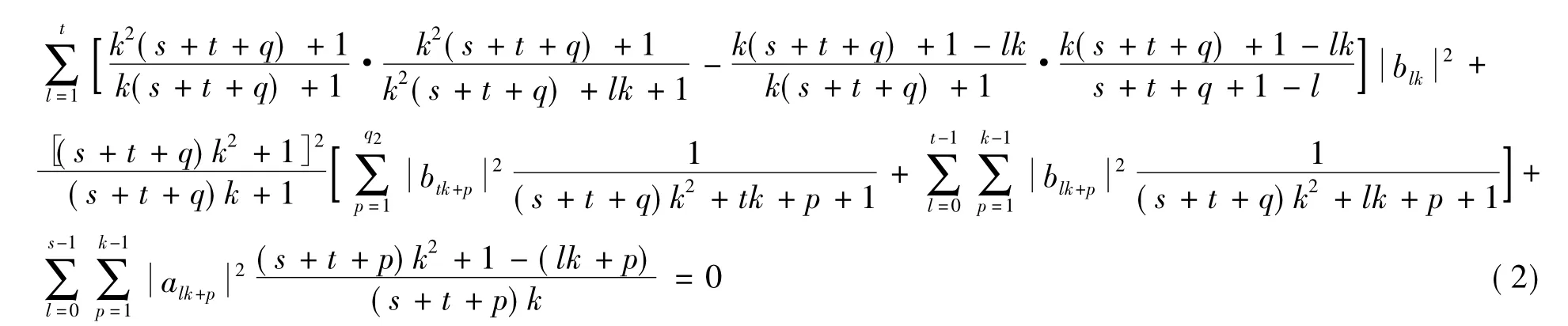
于是由引理1和式(2)可得a0= a1=…= am1= b1= b2=…= bm2= 0，即φ= 0.定理1結(jié)論成立.

3 k階斜Toeplitz算子的亞正規(guī)性

在本節(jié)中我們將對Bergman空間上k階斜Toeplitz算子的亞正規(guī)性展開討論，得到以下結(jié)論.Hilbert空間上有界線性算子A是亞正規(guī)的，若A*A≥AA*.

證明 若φ= 0，則顯然可得Bφ是亞正規(guī)的.若Bφ是亞正規(guī)的，則對任意的f∈A2( D)有

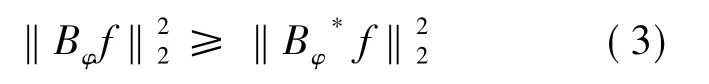
既然m1，m2均為非負整數(shù)，不妨設(shè)m1= sk + q1，m2= tk + q2，其中s，t，q1，q2∈Z+且q1＜k，q2＜k.由f的任意性，不妨取f = z( s+t+q) k，其中q = max{ q1，q2}，于是可得

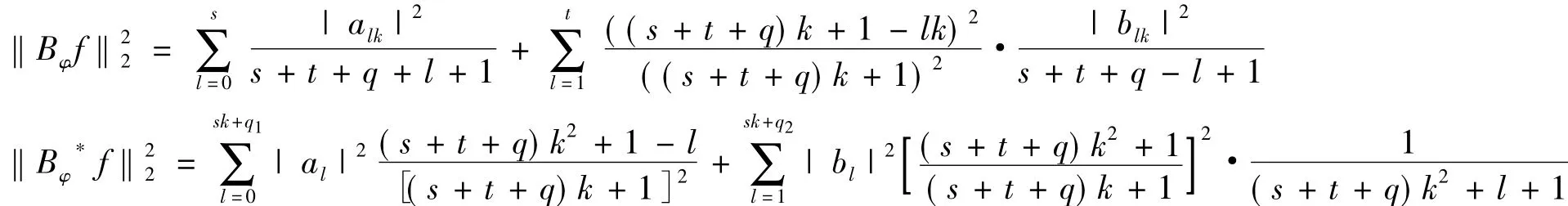
由不等式( 3)可得

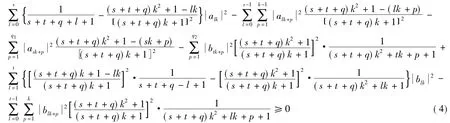
既然對任意的l∈［0，sk + q］，

1;且對任意的l∈［0，sk + q2］，

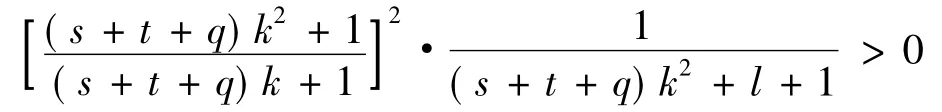
故可得

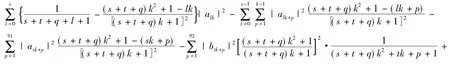
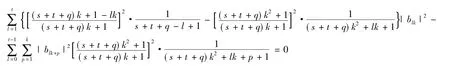
從而可得a0= a1=…= am1= b1= b2=…= bm2= 0，即φ= 0.命題成立.

［1］MARK C HO.Properties of slant Toeplitz operators［J］.Indiana Univ.Math.J.，1996，45( 3) : 843-862.

［2］MARK C HO.Spectra of slant Toeplitz operators with continuous symbol［J］.Michigan Mathematical Journal，1997，44( 1) : 157-166.

［3］MARK C HO.Adjoints of slant Toeplitz operators［J］.Integral Equations and Operator Theory，1997，29( 3) : 301-312.

［4］MARK C HO.Adjoints of slant Toeplitz operators II［J］.Integral Equations and Operator Theory，2001，41 ( 2) : 179-188.

［5］ARORA S C，BATRA R.On generalized slant Toeplitz operators［J］.Indian J.Math.，2003，45( 2) : 121-134.

［6］ARORA S C，BATRA R.On generalized slant Toeplitz operators with continuous symbols［J］.Yokohama Mathematical Journal，2004，51: 1-9.

［7］ARORA S C，BATRA R.Generalized slant Toeplitz operators on H2［J］.Math.Nachr.，2005，278( 4) : 347-355.

［8］安恒斌，蹇人宜.Bergman空間上的斜Toeplitz算子［J］.數(shù)學(xué)學(xué)報，2004，47( 1) : 103-110.

［9］JUN YANG，AIPING LENG，YUFENG LU.K-order slant Toeplitz operators on the Bergman Space［J］.Northeast.Math.J.，2007，23( 5) : 403-412.

［10］YUFENG LU，CHAOMEI LIU，JUN YANG.Commutativity of kth-order Slant Toeplitz operators［J］.Mathematische Nachrichten，2010，283( 3) : 1304-1313.

［11］CHAOMEI LIU，YUFENG LU.Product and Commutativity of kth-order Slant Toeplitz Operators［J］.Abstract and Applied Analysis，2013，45( 2) : 900-914.

Normality and Hyponormality of k-Order Slant Toeplitz Operators on Bergman Space

LIU Chaomei，NI Weidan
( School of Mathematics and Physics，Dalian Jiaotong University，Dalian 116028，China)

The normality and hyponormality of k -order slant Toeplitz operator on the Bergman space are discussed，and obtaining that the necessary and sufficient condition for the normality and hyponormality of k -order slant Toeplitz operator with harmonic polynomial symbol is that its symbol function are zero.

bergman Space; slant Toeplitz operators; normality; hyponormality

A

1673-9590( 2016) 01-0113-04

2015-05-07

國家自然科學(xué)基金資助項目( 11301046，11226120)

劉朝美( 1980－)，女，副教授，博士，主要從事函數(shù)空間及其算子理論的研究

E-mail: lcm@ djtu.edu.cn.