一類粘性四階退化拋物方程弱解的存在性

梁波，張亞杰，彭曦霆，高馨(大連交通大學理學院，遼寧大連116028)*

一類粘性四階退化拋物方程弱解的存在性

梁波，張亞杰，彭曦霆，高馨
(大連交通大學理學院，遼寧大連116028)*

研究一類粘性四階退化拋物方程弱解的存在性問題.在初始函數的一些假定下，首先考慮半離散問題，利用極小元泛函方法證明構造的橢圓方程弱解的存在性;其次構造此粘性四階退化拋物方程的逼近解，通過選取恰當的檢驗函數對逼近解的作一致性估計，得到逼近解的收斂性結果，進而獲得弱解的存在性.

退化拋物方程;弱解;存在性

0 引言

本文考慮如下粘性四階退化拋物方程的弱解問題

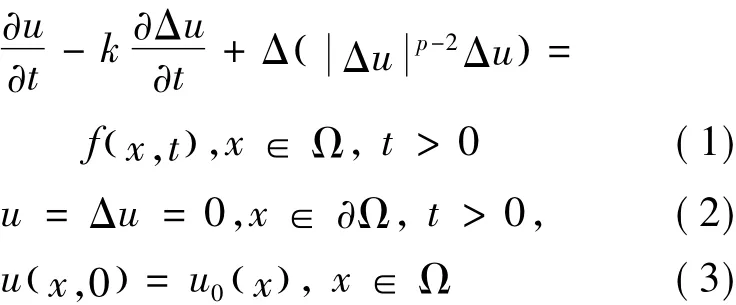
其中，Ω?RN為具有光滑邊界的有界開區域，p＞1為常數，u0( x)為初值函數，k＞0為粘性系數，表示粘性松弛因子或粘性.稱為p－雙調和算子.文獻［1］對于齊次方程情形給出了解的存在性，這里重點關注非齊次情形.方程( 1)為文獻［2］提出的粘性四階退化拋物方程的變形.定義弱解如下:

定義1一個函數u被稱為問題( 1)～( 3)的弱解，若其滿足如下條件:

( 1) u∈L∞( 0，T;C( 0，T; L∞(Ω) )

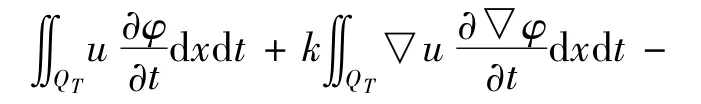
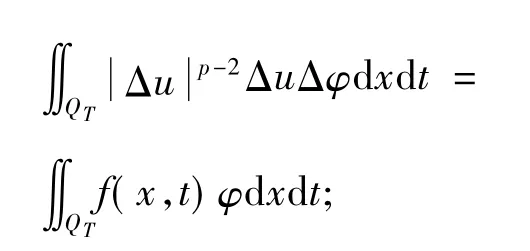
( 3)在L2(Ω)中，u( x，0) = u0( x).

為敘述方便，假設k = 1，當k≠1，時，證明方法相同.本文約定C表示一般的實常數，不同位置也許取值不同.主要結論如下:

定理1 設f∈Lp'(Ω)，，則( 1)～( 3)存在弱解

1 半離散問題

為證明定理1，首先進行時間離散化.設N為正整數，把區間( 0，T)分為N等分，取0，考慮如下橢圓問題

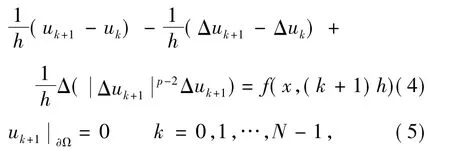
其中，u0是初值函數，f( x，( k + 1) h) = fk+1.

引理1 對固定的k，若uk∈W2，p(Ω)∩，存在H1(Ω)，使對有

這里也稱滿足( 6)的函數uk+1為問題( 4)～( 5)的弱解.

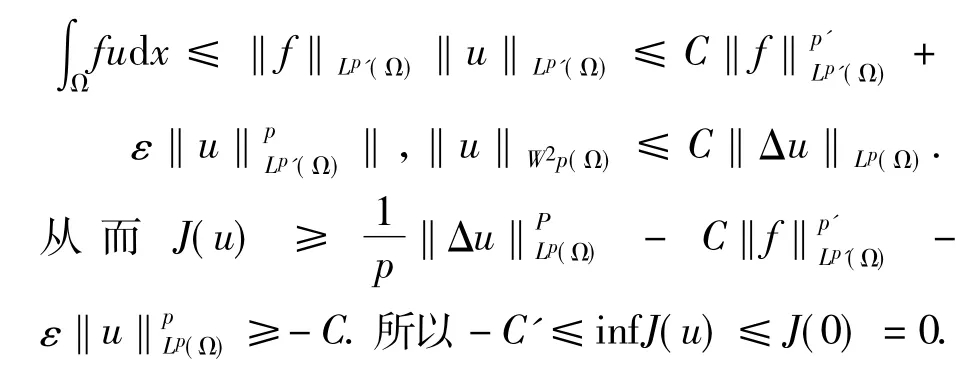
由( 1)知

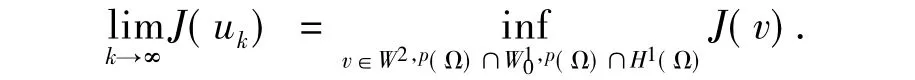
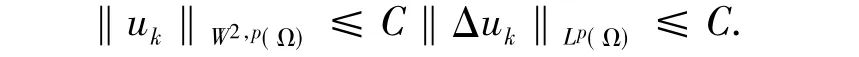
故uk→u弱收斂于，Δuk→Δu弱收斂于

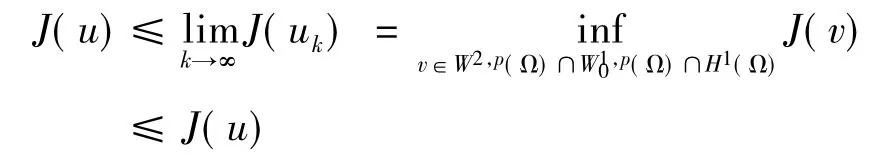
2 弱解存在性

問題( 1)～( 3)的逼近解定義如下:

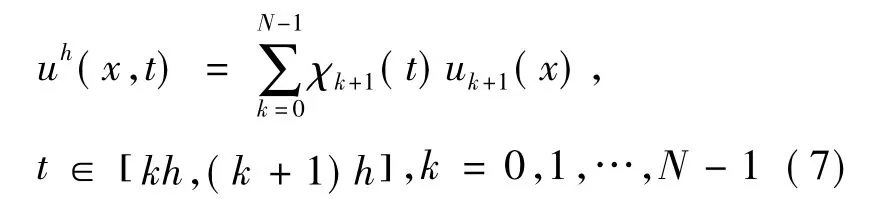
其中，uh( x，0) = u0( x)，χk+1( t)是區間[kh，( k－1)h]上的特征函數.問題( 1)～( 3)所描述的解將由{uh}的某個子序列的極限獲得.為此需要一些關于{uh}的一致性估計.

引理2問題( 4)～( 5)的弱解uk滿足

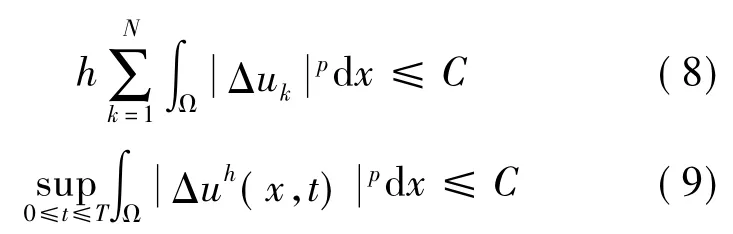
其中，C是不依賴于h和k的常數.

證明 在( 6)中取φ= uk+1，有

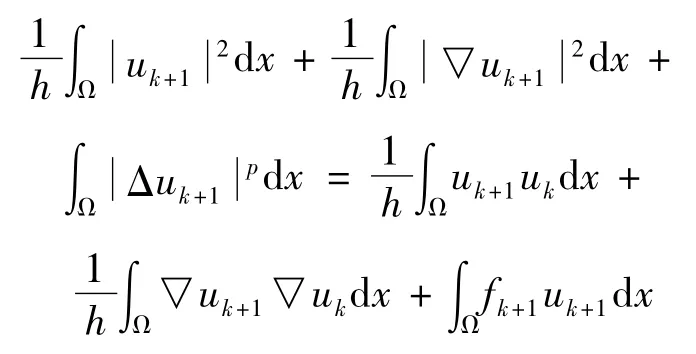
其中，

應用Young不等式并整理，得

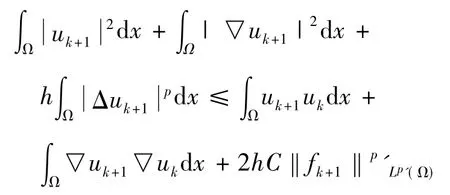
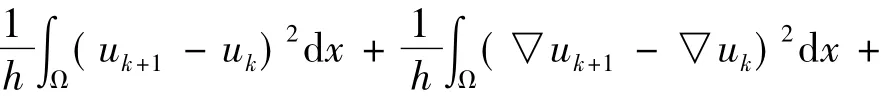
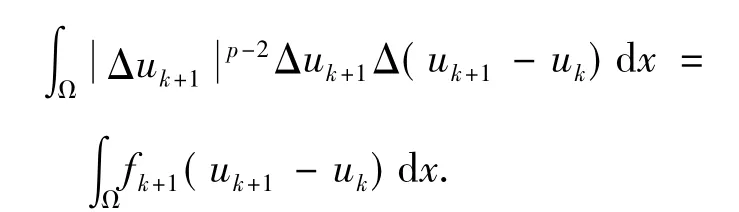
由于上式第二項非負，應用Young不等式，從而有

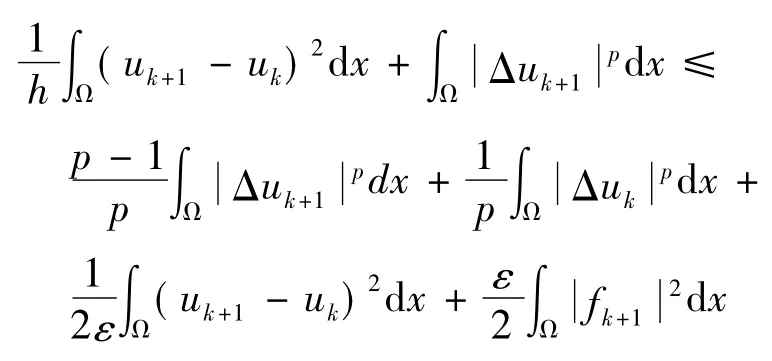
引理3對于問題( 1)～( 3)的逼近解{uh}，存在{uh}的一個子序列(此處及后面都用原來

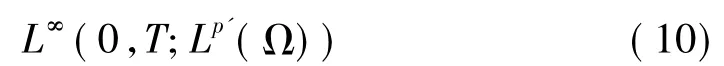
對任意的，取φ( x，( k + 1) h)為檢驗函數，代入式( 6)中，有

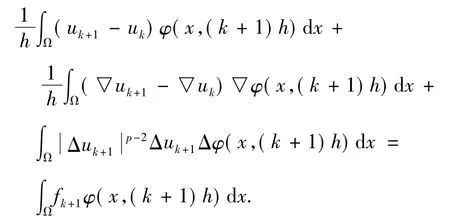
把上式關于k從0～N－1相加，并結合式( 7)和式( 10)且φ( x，Nh) =φ( x，T) = 0，則

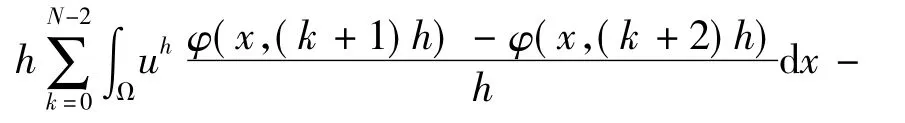
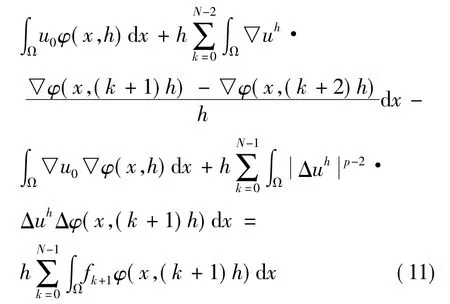
其中，

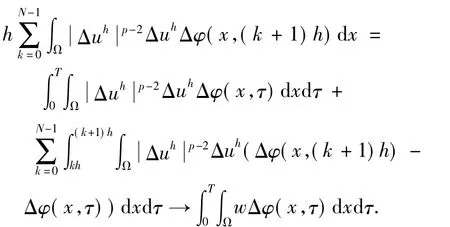
令h→0可得

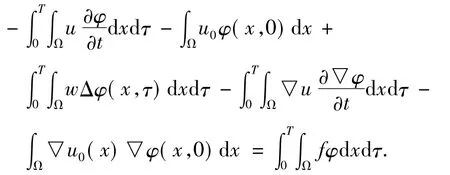
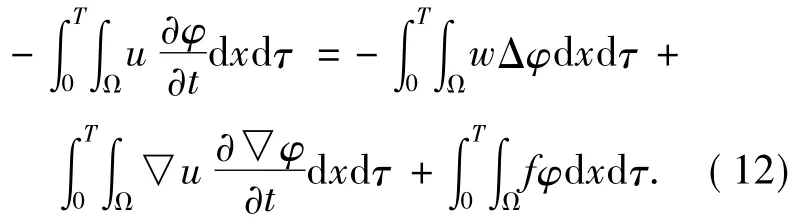
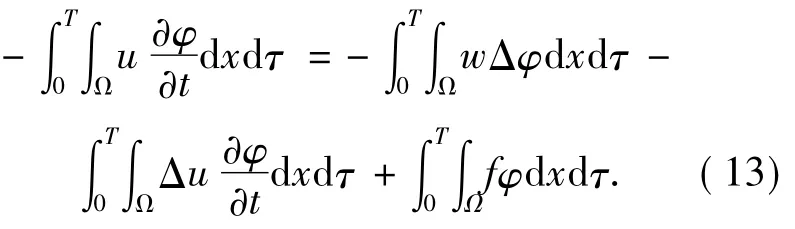
由上式可得

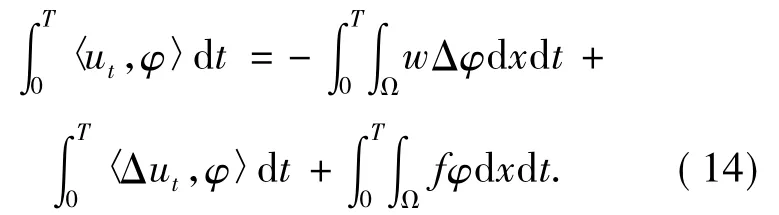
則

即

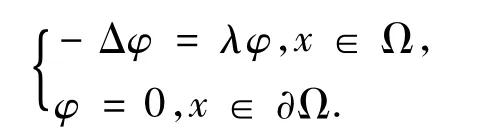
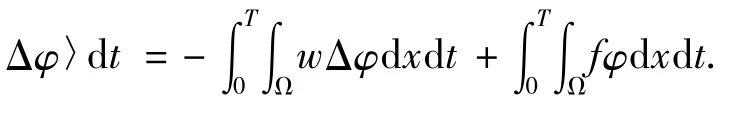
即

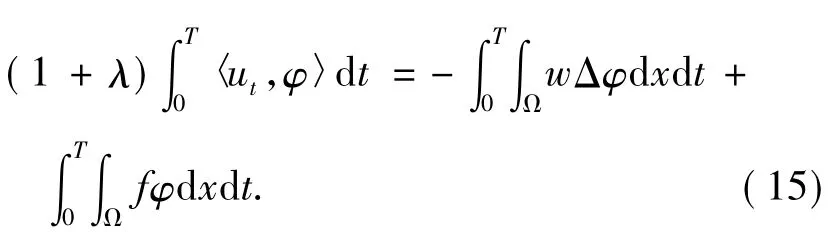
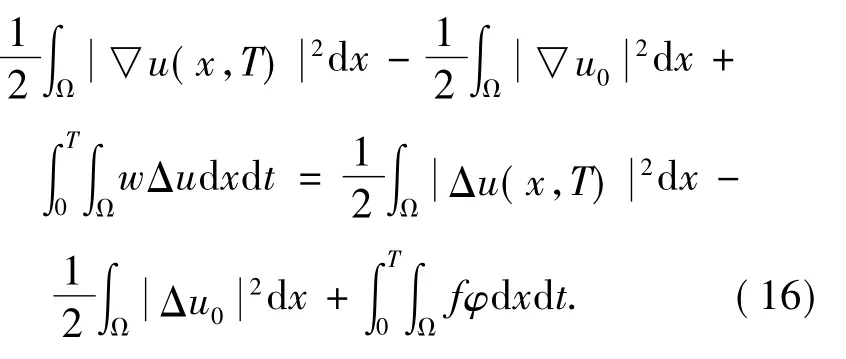
在積分等式( 6)中取φ= uk+1，有

由于任意的檢驗函數φ和ε＞0，以下不等式均成立

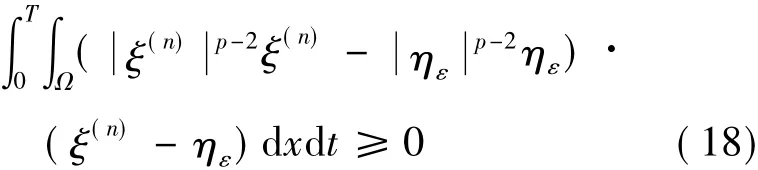
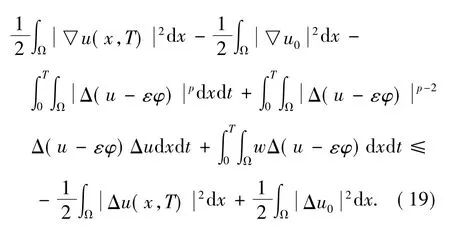
［1］郭金勇.退化擬拋物方程弱解的存在性［J］.南京師大學報(自然科學版)，2013( 2) : 15-19.

［2］COLEMAN B D，DUFFIN R J，MIZEL V J.Instability，uniqueness and non-existence theorems for the equations，ut= uxx－uxtxon a strip［J］.Arch Rat Mech Anal.，1965，19( 2) : 100-116.

［3］陳亞淅，吳蘭成.二階橢圓型方程與橢圓型方程組［M］.北京:科學出版社，1991: 46.

［4］ADAMS R A.Soblev Space［M］.［s.l.］Academic Press，1975.

［5］XU M，ZHOU S.Existence and Uniqueness of weak solutions for a generalized thin film equation［J］.Nonlinear Anal.，2005，60: 755-774.

［6］SIMON J.COMPACT sets in the space Lp( 0，T; B) ［J］.Ann Math Pura Appl.，1987，146( 1) : 65-96.

Study of Weak Solutions to a Fourth Order Degenerate Parabolic Equation

LIANG Bo，ZHANG Yajie，PENG Xiting，GAO Xin
( School of Mathematics and Physics，Dalian Jiaotong University，Dalian 116028，China)

The weak solutions of a class of fourth order degenerate parabolic equation are studied.Under some assumptions on the initial value，the first thing is to cosider a discrete problem.By using minimizer functional method，the existence of weak solution to the elliptic equation is proved.Secondly，the approximation solutions of the four order degenerate parabolic equation are constructed.By choosing reasonable test functions to get the necessary uniform estimations，the convergence results can be obtained and then the existence of the weak solutions is proved.

degenerate parabolic equation; weak solutions; existence

A

1673-9590( 2016) 01-0109-04

2015-05-07

國家自然科學基金資助項目( 11201045)

梁波( 1980－)，男，副教授，博士，主要從事偏微分方程的研究

E-mail: cnliangbo@163.com.