陷阱設在何處

□朱元生

?

陷阱設在何處

□朱元生

平面直角坐標系是“數”與“形”結合的典范，通過平面直角坐標系可以研究數量變化的代數問題和研究位置變化的幾何問題間的相互轉化.而有些同學在解答直角坐標系的有關問題時，由于掌握知識不夠牢固，考慮問題欠周密，常會出現這樣那樣的失誤，現就常見錯誤舉例剖析如下.

一、點的坐標

例1已知點P1關于x軸的對稱點P2（3－2a，2a－5）是第三象限內的整點（橫、縱坐標都為整數的點，稱為整點），則點P1的坐標是______.

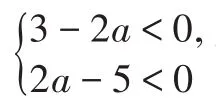
剖析：錯解混淆了關于x軸、y軸及坐標原點對稱的點的坐標之間的關系.關于x軸對稱的點，其橫坐標相同，縱坐標互為相反數；關于y軸對稱的點，其橫坐標互為相反數，縱坐標相同；關于原點對稱的點，其橫、縱坐標均互為相反數.即點P（a，b），則它關于x軸對稱的點的坐標為（a，－b），關于y軸對稱點的坐標為（－a，b），關于原點對稱的點的坐標為（－a，－b）.

正解：得到點P2的坐標為（－1，－1），因為點P1、P2關于x軸對稱，則點P1、P2的橫坐標相同，縱坐標互為相反數，所以點P1的坐標是（－1，1）.

點評：此例考查了直角坐標系內的點在各個象限內的坐標符號以及關于x軸、y軸及坐標原點對稱的點的坐標之間的關系.通過列不等式組求得a的取值范圍，又點P2為整數點，得到a的值，從而點P1的坐標可求.

二、點的變換

例2已知點M（3，－2），將它先向左平移4個單位，再向上平移3個單位后得到點N，則點N的坐標是______.

錯解：點N的坐標為（3＋4，－2－3），即（7，－5）.

剖析：錯解混淆了點的平移方向對應的點的坐標的增減情況.向左平移4個單位，橫坐標減少4，即為3－4＝－1；再向上平移3個單位，則縱坐標增加3，即為－2＋3＝1.

正解：點N的坐標為（－1，1）.

點評：當點P（x，y）在坐標平面內沿水平方向向左或向右平行移動a個單位長度到達點P′的位置時，其縱坐標不變，橫坐標左減右加，這時點P′的坐標為（x－a，y）或（x＋a，y）；當點P（x，y）在坐標平面內沿豎直方向向上或向下平行移動b個單位長度到達點P″的位置時，其橫坐標不變，縱坐標上加下減，這時點P″的坐標為（x，y＋b）或（x，y－b）.

三、圖形的變換

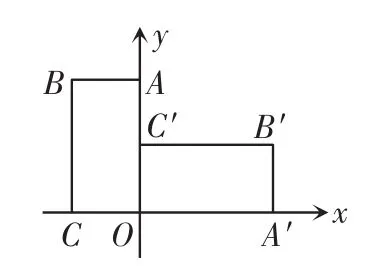
例3如下圖，把矩形OABC放在直角坐標系中，OC在x軸上，OA 在y軸上，且OC＝2，OA＝4，把矩形OABC繞著原點順時針旋轉90°得到矩形OA′B′C′，則點B′的坐標為（）.

A.（2，4）B.（－2，4）

C.（4，2）D.（2，-4）

錯解：A.

剖析：根據圖形的旋轉不改變圖形形狀和大小，所以矩形OA′B′C′的長OA′＝4，寬A′B′＝2，所以點B′的坐標為（4，2）.

正解：C.

點評：把矩形OABC繞著原點順時針旋轉90°得到矩形OA′B′C′，點B′到了第一象限，錯解只注意到點的坐標的符號發生了變化，而疏忽了坐標的數值也發生了變化.

插圖：楊明