HPM視角下課堂教學的“虛”與“實”

仲愛云

[摘 要] 在“一元二次方程的解法——配方法”教學中，幾何方法的探究給“教”與“學”帶來了新的視角，但過分依賴幾何方法，將有損課堂教學. 虛實結合是對HPM視野下課堂教學的深入思考，以史為鑒，注重反思. 教學內容的虛實共濟，即重視針對性，關注發展性；教學方法上的虛實結合，即靈活多變. 教學中應注重學生的實際認知，發展思維虛境，把握虛實的辯證統一關系，讓數學史與數學課堂教學自然融合.

[關鍵詞] HPM； 課堂教學；虛與實

引言

隨著 HPM 研究的不斷深入，數學史和數學教學的結合已是一種國際數學課程改革的趨勢. 數學史在數學教育的實際應用也備受關注. HPM的主旨是將數學史運用于數學教學中，以提升數學學習成效和教學品質. 要擴展數學教育中的歷史維度，需要一個前提，那就是課堂教學中包含一些數學史會取得更好的效果. 為此，數學史內容進入課堂教學有許多“中間環節”需要研究. 以上海市某中學HPM的實驗課“一元二次方程的解法——配方法”為例，談談HPM實踐中的問題、困惑與反思.

問題的提出

方程是代數之花，一元二次方程蘊含著豐富的歷史文化信息. 方程是刻畫現實世界中數量關系的一個有效數學模型，應用廣泛，而從實際問題中抽象出方程，并求出方程的解是解決問題的關鍵. 配方法既是解一元二次方程的一種重要方法，也是推導公式法的基礎. 配方法還是初中數學的重要內容，在二次根式、代數式的變形及二次函數中都有廣泛應用. 下面簡單回顧教學過程如下：

3. 課堂練習

4.課時小結

課堂觀察1：講完例1，引出了配方法的定義. 對于例2，教師讓學生獨立嘗試用幾何方法解方程，但部分學生沒有理會教師的要求，堅持用代數方法解，部分學生用代數方法解出后反推幾何方法.

課堂觀察2：由于x（x-4）=10涉及“x-4”，較例1難，學生思考的時間較長，而且幾何方法構圖方式多樣，教學出現“疙”，費時較多.

問題1：課堂出現了引入時間很長，但練習訓練時間很短的現象，即“頭重腳輕”的現象. 讓大家糾結的是，例2究竟要不要？

執教的老師直言，上課前有老師說不要，但自己覺得好，還是要了. 聽課后，針對例2，大家的討論意見如下. A認為：例1，老師講的，例2，老師又作為例題來講，學生會不會感覺累了？B認為：課堂引入這么長，例2還是不要了. C認為：學生由代數式想到配方法，不是很容易嗎？何苦用幾何方法繞半天？ 這不是為歷史而歷史嗎？去掉挺好，扎扎實實把配方法訓練好，做點“實在”的事情. D認為：例2這樣一個歷史素材真好，棄之可惜……

問題2：融入歷史是一個好的視角，為什么效果不盡如人意？

課堂上“實在”的訓練沒做好，難道是因為數學史融入的影響？其實，在例2幾何方法的探究中，老師講解得有些“吃力”，課堂氣氛一度“沉悶”，并沒有“熱鬧非凡”的花架子，怎么就覺得不實在了？何為“實”，何為“虛”？有為實無為虛、真為實假為虛、客觀為實主觀為虛、顯為實隱為虛、行為實言為虛、已知為實未知為虛、當前為實未來為虛. 羅列了這些不同視角下“虛”與“實”的解釋，HPM視野下課堂教學的“虛”與“實”的意蘊何在？

公元七世紀，印度數學家婆羅芨多也采用了“配方法”，雖然本質與海倫一樣，但在形式上做了改進，在方程的兩邊同乘4a而非a，使得結果更加簡潔.

2. 反思與啟發

一元二次方程來源于實際問題，主要涉及與幾何中面積有關的問題，所以幾何解法成為古代解一元二次方程最常見的方法. 幾何方法是解一元二次方程的本源方法，形式多樣. 解一元二次方程的解法——配方法依賴于開平方法. 方程與其他數學理論一樣，經歷發展的程序：（1）從實際需要，到方法的發現；（2）由方法到理論的形成；（3）理論的建立到實際應用.

現行的課堂教學，不重視從實際需要到方法的發現，以及方法的發現到理論形成的挖掘，重點只會放在第三個環節上，這導致學生雖然解方程游刃有余，可預見解決相關問題的時候，卻束手無策.

從一元二次方程解法的歷史中，我們的啟示有：在教學中，直接涉及數學理論本身，即直接講解“配方法”本身，顯然是不合適的，也就是說，在學習花拉子米代數方法解方程的同時，也不能放棄對幾何方法的探究，不能放棄對數學本源的探究.

古人用幾何方法解一元二次方程，很巧妙，充滿智慧. 古人為什么就能有這么巧妙的方法呢？除了因為一元二次方程問題主要產生于幾何的原因，還有背景是那時沒有符號代數，可以想象，要解決一道題目，用修辭代數表述多么煩瑣，顯然不及幾何方法直觀、明了. 但數學總是不斷發展的，數學家花拉子米在《代數學》用兩種幾何方法解一元二次方程，說明他對一元二次方程問題構造了數學模型，對符號代數、數學理論的發展起到了推動作用.

通過幾何方法講解“一元二次方程的解法——配方法”的一般理論無疑為配方法的數學教學注入了新的視角. 我們也應該注意，由于古今數學發展水平、學習條件和環境的巨大差異，今天，學生對數學概念的認知過程與概念的歷史發展過程之間的相似性只能是相對的、不嚴格的. 就一元二次方程而言，中世紀以前人們對幾何方法的依賴是與修辭代數這一代數學發展的初級水平息息相關的. 而今天，學生在學習一元二次方程之前，已經完成了從算術到符號代數這一代數學高級水平的過渡. 我們的目光不能僅僅停留在過去，對于歷史的遺留，除了繼承，還應發展. 用發展的眼光審視歷史，啟示我們教學中既要索源，也要引流. 一元二次方程幾何方法與代數配方法是“數形結合”自然的范本，但不能過分依賴幾何方法.

設計歷史套裝：虛實結合，追求本質融合

1. 歷史材料的顯與隱

對于例1“ 一平方與十根等于二十迪拉姆平方，求根. 即求方程x2+10x=20的根”，可改進為：

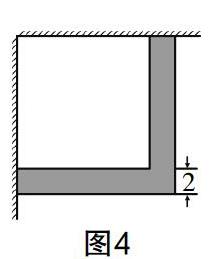
如圖4，已知一座房子的角落有一空地，想建成一個正方形小花圃，已知正方形的面積與周長的和為20，在其周圍留寬為2的小路，小路上鋪上地磚，求所需地磚的面積.

理由：直接置于一個幾何背景中，體現了一元二次方程源于實際問題，也會讓學生更加自然地接近幾何方法. 同時隱去“迪拉姆”“古人”等無關緊要的話語，語言簡潔、流暢，歷史素材的使用簡單明了，不著痕跡.

歷史素材可以提高我們數學課堂教學的品質，滲透文化的要素，但不是說直接引入. 抽取歷史中能實實在在引起學生思維沖突、促進學生思維、激發學生學習斗志與興趣等本質的東西以及課堂中學生學習確實需要的要素，把這些呈現出來，這就是“實”. 不要把歷史史料和盤托出，可隱去一些元素，如學生難以理解的古文等，因為過多這些元素的加入可能會無形中加大數學課堂學習的難度，干擾學生的注意力，沖淡學生理解數學主題.

古人云：“不全不粹之不足以為美.” 全，在我們這里應該指的就是實；粹，就是隱略或去掉粗的部分. “洗盡塵渣，獨存孤迥”，歷史材料在課堂中追求“全”和“粹”的辯證統一，則課堂教學自然會多幾分美的欣賞.

2. 數學思想與知識的虛與實

解一元二次方程，幾何方法的介入是對傳統教學直接講解配方法、單純用代數方法的一次大大改進，讓人耳目一新，為學生構建數學問題的幾何模型提供了很好的素材，以致老師例1講了幾何方法，例2繼續深入，舍不得丟了例2. 例2相對于例1來說，更能讓學生深入思考，可是例2影響了一節課的教學效果，因為例2的講解，后來已沒有時間展現代數方法配方的一般步驟，課堂練習訓練不到位. 這是“實”沒做好. 如何利用好例2這個好素材？借用一點“明修棧道，暗度陳倉”的策略. 明面上，讓學生扎扎實實掌握配方法，可以把例1學得更深入，在例1的幾何方法之后，深入分析數與形之間的關系，同時給出配方法的定義和一般步驟. 呈現歷史上海倫和婆羅芨多的配方法，讓學生比對各種方法，同時在板書、訓練等方面做實、做好. 例2可以留作練習，在眾多練習中，選一題（例2）給出幾何構圖，暗地里悄悄滲透數形結合的思想，潤物無聲，看似“虛”，其實是真正的意圖、長遠的目標.

整合歷史，吃透數學歷史的精髓，擬成這節課的“虛線”和“實線”. 虛線是數形結合的數學思想，實線是讓學生掌握解決一元二次方程的配方法. 虛與實是課堂的兩翼，“避實就虛”或“就實避虛”都不可取，僅有哪一方面都會給數學學習帶來不可彌補的缺憾.

兵法之：虛則實之，實則虛之，虛和實是矛盾統一體. 從這節課來看，實是代數配方法，虛是數形結合. 從長遠看，數形結合是數學本質的思想方法，是實的，而這節課的具體知識是載體，是虛的. 虛實并御、虛實互濟還需要一種整體性的教學思維，即從這節課出發，從一元二次方程的概念，到解一元二次方程的直接開平方法、因式分解法、配方法、公式法等，整體配置數學史料. （見表1）

這樣便在教學配方法之前充分體現了方程來源于實際問題，凸顯了幾何背景，為配方法中幾何方法的探究做鋪墊，節省了這節課引入的時間，為后面的“實”留下了空間. 在每一節課中，“數形結合”隱隱滲透，是虛線，但每一節都滲透一點，卻把數形結合的思想滲透做到了實處.

課堂演繹：虛實相生，追求自然融合

1. 課堂教學結構的虛實

狄德羅說：“美在關系. ”虛與實是一種結構性的關系，虛實關系的研究就是對虛實美學結構的研究. 課堂中的虛實是一個立體性的結構模型，虛中有實，實中有虛. 課堂教學也有結構的美，頭重腳輕、前松后緊或前緊后松等都是不可取的. 在課堂上，哪些應該呈現出來，或者還要重點標注，顯示出來，哪些不該顯示出來，都應該有所講究. 在呈現的歷史史料中，有的故事或美麗的圖片、詩歌等，如果用于激發學生的情趣，呈現的時間要短，可以放在學生一小段緊張的思維勞動后；對于啟迪思維的本質要素，呈現的時間則要長. 課堂教學的虛實猶如太極拳，有快有慢，有徐有疾. 這節課過多的時間用于顯示幾何方法，代數方法這個實沒有顯示好，代數配方法沒有有效穩固好，會影響虛，即所謂的以實才能出虛. 虛是指導思想，知識是一個載體，以虛出實. 虛實結合，才能化實為虛.

2. 教學方式的虛實

好的史料很多，但要仔細揣摩，講究科學的教學方法，使其很好地融入課堂. 如果僅僅機械拼湊，教學方法不是有虛有實，就不能虛實交融. 例1、例2是一個類型，例2是在例1的基礎上構圖思路稍微復雜一些. 如果還用相同的教學方法，勢必有一種“疲勞感”. 課后，有老師評論說例2會不會讓學生覺得累了，累與不累也許可以不深究，但同一類例題，用相同的教學方式，不可取. 課堂教學中的虛實就是說不能平均用力，要有著力點，當然也有輕松點. 靈活多樣的教學方式、手段肯定受學生歡迎. 既然例1已經仔細講解、深入分析了，這就是“實實在在”，那例2就可以放手讓學生自由發揮，換一換形式，由課內到課外. 不是所有的好東西都要老師講，講多了，嚼爛了喂給學生，學生吃了反而不會覺得香. 人們時常說課堂教學有留白藝術，即虛實結合. 沒有通過虛與實的碰撞，就不會有交感、產生新質，而是一覽而盡，略無余韻.

3. 學生思維的實意與虛境

在例1幾何方法的探究中，有學生試著用代數方法配，即x2+10x=（x+5）2，盡管結果不對，但學生有了化歸“直接開平方法”的意識，但老師沒有理會學生. 由例1給出配方法的定義后，對于例2，很多學生直接用代數方法，那也是自然的事情，可老師“強拉”學生用幾何方法，此時，學生不會覺得幾何方法好，也不會領略到古人“思維”的魅力. 其實，這節課的歷史相似性有些出入，原因在于學生的頭腦中已有符號代數. 如果我們從學生的“實際”思維意圖出發，順勢而下，做實學生的代數方法，介紹花拉子米的歷史功績，介紹“algebra”的由來（與解方程有關），順勢介紹花拉子米的幾何方法，海倫和婆羅芨多的配方法，就能讓學生比較自己與古人的方法，縱觀古人代數方法的不斷改進，比較幾何方法與代數方法，體會數形結合，體會代數符號的作用，提高判斷能力，增強批判意識. 其實，古人無論是幾何方法還是代數方法，都是為了更簡潔地表達與解決問題，這是數學求簡精神的體現. 如果學生在體會中悟出這些，就能真正走進古人的心靈. 數學史融入數學教學與學習中的一個重要作用就在于培養人的才、學、識. 現在的教育重視“學”，即學知識，也強調“才”，即能力，但對“識”重視不夠. “識”，即見識，是引導知識和能力走向何方的根本性問題，屬于對知識融會貫通之后的個人見解，其背后的支撐是世界觀、人生觀. 數學史的作用恰恰在此體現.

從學生的實際思維出發，做實代數方法，利用幾何方法等史料開拓“思界”，營造“虛”境，讓學生穿越時空，與古人來一次對話，可謂今有代數方法、古有幾何方法. 在自我體會中，加深對數學知識的理解，形成數學思想，領悟數學精神.

結語

以虛為本，以實為用. “以史為鑒”的數學課堂的虛境（數學思想滲透）的提煉，提升了數學課堂的文化品位；虛又需借實去表現，使重心落到實上，以實為用. 在虛的統運之下，實者逼肖，而虛者自出. “虛實結合”是數學史融入數學課堂的一種狀態，糅合了數學史融入課堂的多種方法和途徑，既重視針對性又關注發展性.

一線教師的大膽嘗試所展示出的“理念”影響了我們甚至更多人，給我們帶來了無盡的思考，這是可取之處. 數學史給數學教學帶來了興奮點，但我們必須認識到HPM視野下的數學課堂需要精耕細作，粗放式的融合將損害課堂教學，不能讓人信服. 只有恰當地、適時地深度融合，做到簡單而精巧，自然而不生硬，既“上得廳堂”，又“下得廚房”，既出現在公開課的“秀”上，也出現在日常課堂中，數學史與數學教育才會走出“高評價、低運用”的實然困境，發揮出它的應然向度.