立木材積與地徑關系探析


【摘要】:實際工作中,經常遇到無法實際測出到原木而要求從地徑確定立木材積。但是目前還沒有現存的利用地徑測算立木材積的統一方法。本文主要是介紹探析這一方法的過程和方法,從而揭示立木材積與地徑的函數關系。進而提高各單位對林木問題處理的效率。
【關鍵字】:試驗地概況 ;遺傳算法 ;三次設計法
實際生活中,對濫砍濫伐,盜砍盜伐等案件的追查以及林木糾紛問題的處理都需要確定立木材積。過去往往是實測地徑并根據周邊地段林木的生長狀況估計該林木的胸高直徑,然后由一元立木材積表查出立木材積,這給工作帶來了很大的困難。
1、 試驗地概況
珙縣位于雪峰山北邊北緯27°-28°.山地地貌。年平均氣溫16℃.最高海拔1620m,最低海拔57m.土壤以紅黃壤,黃壤為主。植被屬于亞熱帶常綠闊葉林帶。多以馬尾松,常綠闊葉林以及杉木為主。
2、研究方法
2.1首先選擇標準地。在范圍內設置21塊標準地,面積均為20×20m2。其中10塊為杉木,闊葉林5塊,馬尾松6塊。每一塊標準地內各徑階林木的株樹必須為按正態分布,否則標準地不合格,需重置。確定標準地后,在標準地內選取最小徑級和最大徑級各一株和平均木3或4株作為樣本。
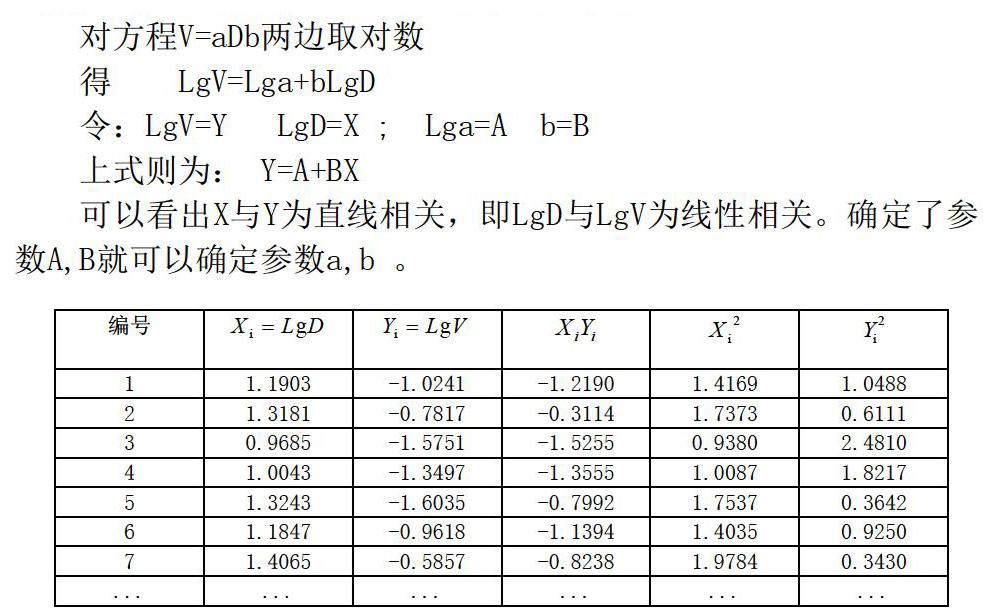
2.2遺傳算法。遺傳算法是一種優化迭代算法,他基于生物學進化原理。他的基本思想是利用材積方程V=aDb,將其解表示成“染色體”,從而構成一群染色體,根據自然界適者生存原則從中選擇出適應該環境的染色體進行復制,通過變異交換產生新一代更適合環境的染色體群。如此反復,經過若干代的繁衍變化,最后收斂到一個最優適應個體上,從而得出最優解。
2.3三次設計法。三次設計法包括系統設計,參數設計和容差設計。對質量管理對策尤為重要的是參數設計。利用方程V=aDb的可算性,利用正交表進行優選,選定的目標函數是殘差平方和最小,再由計算結果來確定該方程的參數組合。對于設計參數正交表通過多分位級的方式適當增加行數。
3、檢驗適用性
任何科學研究結果都必須檢驗其適用性,需要進行檢驗。
檢驗對象為實際測出的材積值( )和相對應的胸徑、樹高的材積方程計算的理論值 。當實測值與理論值相同時就形成直線回歸方程 。且當a=0,b=1時才能得出方程V=aDb適用該地區;若a≠0或b≠1則表示兩者之間有誤差,需要重新檢驗。
F檢驗結果表明遺傳算法和改進單純形法計算的理論材積和實際的測量數據差異很小,而三次設計法和對數線性最小二乘法與實際材積有很大差異。
4、最小二乘法材積方程的建立
回歸分析法:分別將馬尾松、闊葉樹以及杉木的立木材積和相應地徑曲線圖形描繪出來。可以看出三種樹立木材積對地徑均為冪函數相關。即方程V=aDb,其中a、b為參數,確定了參數a、b就可以確定V和D之間的函數關系。計算過程如下:
根據同樣的算法,我們可以得到:馬尾松立木材積對地徑的回歸式:V=0.00017740D2.4852;闊葉林樹立木材積對地徑的回歸式:V=0.0000537887D2.6384 。
結果表明,用遺傳算法、三次設計法和改進單純形法等建立的材積方程V=aDb時,三者的殘差平方和約為0.05488,明顯安小于最小二乘法的0.07318,三者的關系數也明顯高于后者。因為取對數擬合方程V=aDb是在兩邊取對數的情況下再進行最小二乘回歸分析的,此時對方程LgV=Lga+bLgD而言是最優的,但是對于原方程V=aDb卻不一定了。而本文講述的方法則是直接采用全局優化的方法求解參數值的。因此,就擬合的精度而言遺傳算法和三次設計法明顯更優于對書線性化最小二乘法。
5、討論
用遺傳算法。三次設計法等方法擬合的材積方程V=aDb參數的組合過程是尋求a和b,將冪曲線回歸方程的殘差平方和以最小,效果比傳統的最小二乘法效果更為理想。本文所講述的三種方法所得的材積方程V相關系數在0.93以上,相關顯著。
2.立木材積表的種類和區別
立木材積表分為一元立木材積表和二元立木材積表。一元立木材積表的自變量是平均胸徑,應變量為平均材積。沒有考慮樹高的影響。但事實上樹高,斷面積,形數對林木的材積都有影響。所以二元材積表就考慮了樹高和胸徑兩種因素對它的影響。計算林木材積地方法有很多種,首先一種是區分求材積法,而另一種是根據調查所得的數據查一元或者二元的材積表。
6、杉木與馬尾松及闊葉樹地徑材積表的編制
目前為止,用于林業調查設計和資源管理過程中起重要作用的測樹用表還不夠標準化、規范化,與當前的需求不相適應。
地徑材積表作為一種測樹用表也是森林經營和采伐管理的重要參照。編制地徑材積表是為了給資源監測,林政處罰以及司法公正時涉及到估測林木蓄積提供科學依據。
綜合對地徑的測定和變化的規律以及實際應用的需要進行考慮,將測定部位選在離上坡地面0.1m處。選擇的部位如果低了,隨著采伐利用程度的提高,該部位將很難找到;如果太高了,則會出現地徑的變化異常。對于實驗地中的林木,除了個別的地徑生長異常予以剔除外,對其他的每株活樣本都采取離上坡地面1.2m出的胸徑和0.1m處的地徑進行測量。
首先我選擇以下兩種方程進行比較:
線性方程:Y=A+BX;二次拋物線方程:Y=A+BX+CX2
其中的Y均為離上坡地面距離的胸徑值;X表示地徑值;現規定剩余標準差為S、相關系數為R、檢驗值為F ;作如下比較:線性方程Y=A+BX
根據共識的計算結果表明兩種方程的回歸效果均較好,但是二次拋物線方程的相關系數,攝于標準差效果更好,因而選擇二次拋物線的關系式更好即:Y=A+BX+CX2
將地徑帶入到不同樹種的拋物線方程中,即可估計出相應樹種的胸徑值,再將估算出的值帶入到立木材積表的公式中進行計算即可得到該地徑材積。
在樣地調查中隨機選取一部分樣本的實測值座位地徑材積表適用性檢測的依據。
7、結論
采用固定樣地的方式對不同樹種的地徑和胸徑進行復查,用以編制地徑材積表不僅僅可以減損人力消耗還可以節省財力。這種方式所制定的表格不僅量大,而且隨機,因此具有可靠性。其次,得出的函數關系再經過適用性檢驗后,發現實際數據與理論值差異可忽略,因而具有高準確度的優點。該研究在胸徑立木材積的精度和地徑材積具有決定性作用,并且可以在加強林正資源管理和提高林業經營管理水平等方面發揮更大的作用。
【參考文獻】:
[1]洪偉,吳承 試驗設計與分析——原理,操作,案例。中國林業,2014:50-60;
[2]喬紅秀,李朝暉——中國生態發展。中國工程,2015:107-190;
[3]郭敏遠,鄧暉,匡民森——林木培育的可持續發展道路。長江出版社,2013:45-76;
作者簡介:梁元平(1974-7-16),男 ,漢族,四川省宜賓市珙縣人,大專,林業工程師(中級);從事林業資源管理方面工作。

