周期結(jié)構(gòu)帶隙的能效觀點(diǎn)
周 俊,饒柱石,塔 娜(.上海交通大學(xué)振動(dòng)、沖擊、噪聲研究所,上海0040;.上海交通大學(xué)機(jī)械系統(tǒng)與振動(dòng)國家重點(diǎn)實(shí)驗(yàn)室,上海0040)
?
周期結(jié)構(gòu)帶隙的能效觀點(diǎn)
周俊1,饒柱石2,塔娜2
(1.上海交通大學(xué)振動(dòng)、沖擊、噪聲研究所,上海200240;2.上海交通大學(xué)機(jī)械系統(tǒng)與振動(dòng)國家重點(diǎn)實(shí)驗(yàn)室,上海200240)
摘要:在幾何構(gòu)型或材料特性方面具有空間重復(fù)特性的一類結(jié)構(gòu),稱為周期結(jié)構(gòu),如桁架、加強(qiáng)筋板等。在一定頻率范圍內(nèi),周期結(jié)構(gòu)能夠阻斷彈性行波在其中傳遞,該特性可應(yīng)用于隔振器開發(fā)。現(xiàn)有周期結(jié)構(gòu)隔振分析大多基于無限長假設(shè),即假設(shè)周期結(jié)構(gòu)在幾何空間中可無限延伸,因此只有行波解具有物理意義,非行波模式則被忽略。然而,工程中隔振系統(tǒng)都是有限長的,因此非行波解的確存在,故其能量傳輸特性具有研究價(jià)值。周期桁架有限元數(shù)值仿真結(jié)果表明,周期結(jié)構(gòu)行波解的功率因數(shù)始終等于1,說明頻散曲線與能量傳輸效率有關(guān)。據(jù)此引入效率指標(biāo)函數(shù),通過其響應(yīng)表面局部極大值、極小值的連線,將頻率-波數(shù)空間劃分為能量傳輸高效區(qū)和低效區(qū)。該劃分方式能統(tǒng)一處理行波解和非行波解的情況,拓展原有帶隙分析適用范圍,為有限周期結(jié)構(gòu)能量傳輸效率分析提供新途徑,對于隔振器開發(fā)設(shè)計(jì)具有重要參考價(jià)值。
關(guān)鍵詞:振動(dòng)與波;周期結(jié)構(gòu);功率因數(shù);效率;帶隙;桁架
周期結(jié)構(gòu)理論起源于牛頓在計(jì)算聲速時(shí)所引入的一維彈簧振子鏈模型[1],隨后在多個(gè)物理學(xué)分支中被廣泛應(yīng)用,例如金屬導(dǎo)電性問題[2]。所謂周期結(jié)構(gòu),就是指一類具有單元重復(fù)特性的結(jié)構(gòu),例如晶體就是由晶胞在空中重復(fù)陣列而形成的。此類結(jié)構(gòu)最為重要的特性之一就是對某些頻率的行波(光波、彈性波等)具有阻斷作用,或者說特定頻率范圍內(nèi)的行波,在周期結(jié)構(gòu)中無法傳遞,該特定頻率范圍稱為帶隙、阻帶、禁帶。對于宏觀周期性固體結(jié)構(gòu),例如桁架、鐵軌、加強(qiáng)筋板等,對固體中的彈性波能形成帶隙,因此,在振動(dòng)噪聲控制領(lǐng)域,周期結(jié)構(gòu)被視為一種有效隔振手段,受到廣泛關(guān)注和研究[3- 5]。Bondaryk對周期桁架隔振特性進(jìn)行研究,證實(shí)其具對彈性波具有低通濾波器特性,能較好地抑制高頻振動(dòng)傳遞[6]。黃修長等設(shè)計(jì)具有較低阻帶中心頻率的曲梁周期結(jié)構(gòu),可用于機(jī)械設(shè)備隔振支撐[7]。肖勇等對具有周期減振支撐的管道的彎曲波帶隙特性及其形成機(jī)制進(jìn)行深入研究,指出通過調(diào)節(jié)減振支撐間距與參數(shù),可以使局域共振帶隙與布拉格帶隙發(fā)生耦合,從而有效拓寬阻帶頻率范圍[8]。尹劍飛等將周期結(jié)構(gòu)能量隧穿效應(yīng)納入周期加強(qiáng)筋板的統(tǒng)計(jì)能量分析中,從而提高了子系統(tǒng)響應(yīng)預(yù)測精度[9]。Mei等將周期結(jié)構(gòu)帶隙與局域共振原理結(jié)合,設(shè)計(jì)一種薄膜式聲超材料,其對空氣中低頻噪聲具有強(qiáng)烈吸收作用[10]。Yan等設(shè)計(jì)由混凝土包覆、內(nèi)嵌橡膠和鐵芯的元胞,由元胞組成的三維周期性地基,可用于上層建筑物抗震[11]。Wang等利用屈曲狀態(tài)下梁剛度可變這一特性,實(shí)現(xiàn)了帶隙中心頻率可調(diào)節(jié)的周期結(jié)構(gòu)[12]。
周期結(jié)構(gòu)隔振特性分析的一般步驟是:首先計(jì)算無限長周期結(jié)構(gòu)的帶隙[13],從而確定振動(dòng)傳遞的衰減頻率范圍,然后在有限周期結(jié)構(gòu)上,根據(jù)具體邊界條件,計(jì)算振動(dòng)傳遞率,確定有限長情況下的振動(dòng)衰減量以及衰減頻率范圍。在振動(dòng)帶隙分析中,以行波解為主,忽略振幅隨空間程指數(shù)衰減的倏逝波解——近場解。然而,現(xiàn)實(shí)中隔振系統(tǒng)都是有限長的,因此倏逝波解的確存在,對振動(dòng)傳遞特性必然產(chǎn)生一定影響,例如隧穿效應(yīng)[14],所以有必要對周期結(jié)構(gòu)非行波解的能量傳輸特性做進(jìn)一步研究。
利用有限單元法,對有限周期桁架在一般情況下的能量傳輸效率進(jìn)行計(jì)算,通過效率指標(biāo)函數(shù)響應(yīng)表面[15]的局部極大值、1/2局部極大值以及極小值分布,將頻率-波數(shù)空間,劃分為一系列能量傳輸高效區(qū)和低效區(qū)(對應(yīng)隔振區(qū))。上述劃分方式為有限周期結(jié)構(gòu)的能量傳輸特性分析提供新途徑和視角,對隔振器的設(shè)計(jì)和開發(fā)具有重要參考價(jià)值。
1 帶隙理論回顧
1.1一維縱波
為了與周期結(jié)構(gòu)中行波解作對比,不妨首先回顧均勻介質(zhì)中的一維縱波。眾所周知,等截面細(xì)長桿中的單列縱波解可表示為

式中v表示縱向振速,譜系數(shù)v?表示波幅以及相位。令桿中橫截面的縱向拉力N為
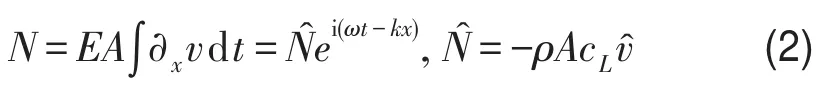
上式中cL為縱波波速,負(fù)號是由于截面正應(yīng)力取拉為正造成的。該式表明,右行波解的截面內(nèi)力與縱向速度之間的相位相差180°,注意到截面拉力N所做的時(shí)均功率Pˉ計(jì)算式為
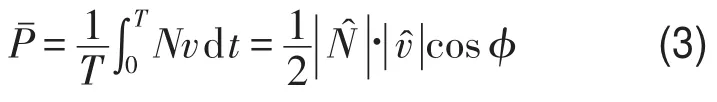
式中cos?稱為功率因數(shù)。
根據(jù)以上討論可以得出行波解具有如下兩個(gè)重要特性:
特性1.由式(1)和式(2)可知,沿波傳播方向上,截面狀態(tài)變量(力、速度等)幅值相等,且滯后的相位差相同,即
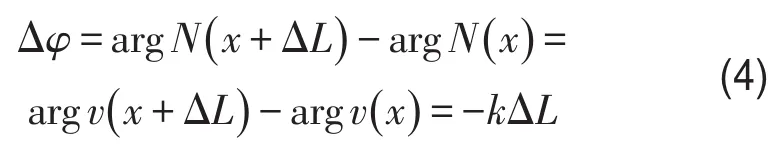
式中N和v如圖1所示。
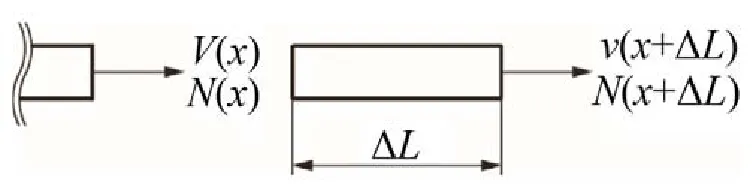
圖1 截面狀態(tài)變量
特性2.由式(2)和式(3)可知,截面內(nèi)力功率的功率因數(shù)等于cos?=?1,換句話說,行波解是以最大效率的方式傳輸能量(行波解內(nèi)力所做的無工功率為零)。需要說明的是:特性1和2之間是相互獨(dú)立的。特性2與應(yīng)力-應(yīng)變關(guān)系有關(guān),無法由特性1直接推出。
除了從功率因數(shù)角度衡量能量傳輸效率以外,還將引入效率指標(biāo)η來衡量傳輸過程中所需付出的能量代價(jià)問題。注意到功率是力與速度的乘積,滿足傳輸功率不變的前提下,如果輸入端驅(qū)動(dòng)力過大,容易誘發(fā)承載件的疲勞破壞,影響使用壽命;另一方面,如果驅(qū)動(dòng)力不大,但輸入端振速過大,則意味著浪費(fèi)在粘滯損耗上的功率在加大,換句話說,輸入端所需付出的動(dòng)能和應(yīng)變能之和越小越好。因此,可以將功率與輸入端比機(jī)械能(單位質(zhì)量的機(jī)械能)之比作為另一種能量傳輸效率指標(biāo)

相比于功率因數(shù),指標(biāo)η還考慮了輸入端驅(qū)動(dòng)力和速度,因此是一個(gè)綜合性能指標(biāo)。注意到縱波時(shí)均功率計(jì)算式為以及
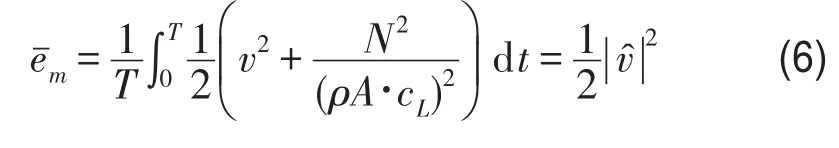
代入式(5)得到單列縱波的效率指標(biāo)η=1。指標(biāo)η的物理意義是:在輸入端,每增加單位比機(jī)械能,傳輸功率的提高量為ρAcLη,顯然η越大,相同傳輸功率條件下,在輸入端所需維持的場能越小。進(jìn)一步可以證明,如果存在反射波,則η<1,這意味單列行波模式具有如下特性:
特性3.單列行波解的能量傳輸效率指標(biāo)η取到最大值。
由一維縱波特性2和3可知,從能量傳輸效率角度,行波解具有顯著地位。那么對于周期結(jié)構(gòu)中的行波解,是否也具有特性2和3則有待進(jìn)一步驗(yàn)證。
1.2周期結(jié)構(gòu)帶隙
在周期結(jié)構(gòu)中,如果在某些頻率范圍內(nèi)找不到行波解,說明振動(dòng)能量的傳遞在此頻帶內(nèi)受到抑制,這一特殊頻率范圍就是所謂帶隙。以圖2所示的一維周期結(jié)構(gòu)為例,假定其兩側(cè)均可無限延伸,現(xiàn)截取若干個(gè)元胞(周期)作隔離體分析,并令左側(cè)為輸入端,右側(cè)為輸出端。設(shè)輸入/輸出端的簡諧內(nèi)力和振速分別為和
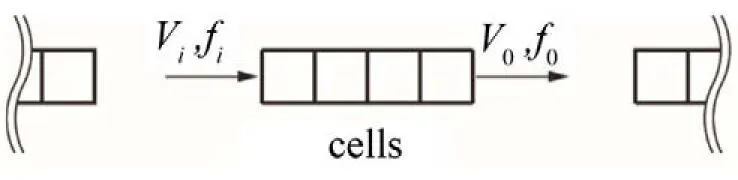
圖2 一維周期結(jié)構(gòu)示意圖.
一維周期結(jié)構(gòu)行波解的判定準(zhǔn)則如下[16]
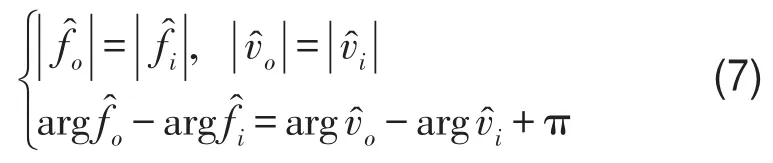
式中+π的原因是由于輸入/輸出端截面外法線方向不一致造成的,該判定準(zhǔn)則本質(zhì)上等價(jià)于行波特性1。需要注意的是,單純依靠式(7)同樣無法判定周期結(jié)構(gòu)行波解的功率因數(shù)cos?是否一定等于1。
令圖2中隔離體的輸入/輸出端的振速幅值比為λ

根據(jù)判定準(zhǔn)則式(7)可知,λ=1是周期結(jié)構(gòu)行波解的必要而非充分條件,換句話說滿足λ=1的解并不一定就是行波解。在某些情況下,駐波解同樣可以滿足λ=1的條件;除行波解外,周期結(jié)構(gòu)還可存在倏逝波解,此類解的特點(diǎn)是波幅隨空間坐標(biāo)增加而指數(shù)增長或衰減,顯然此時(shí)λ≠1。
如果采用無限周期結(jié)構(gòu)假設(shè),這意味著倏逝波解不具有物理意義。事實(shí)上,倏逝波解的振速幅值將在正或負(fù)無窮遠(yuǎn)端發(fā)散,因而通常不予考慮。然而,對于一般工程結(jié)構(gòu),無限周期假設(shè)并不十分恰當(dāng)。注意到工程結(jié)構(gòu)都是有限長的,無限周期假設(shè)僅僅是一個(gè)理想假設(shè),因此在應(yīng)用周期結(jié)構(gòu)帶隙特性進(jìn)行隔振器開發(fā)設(shè)計(jì)過程中,如果完全排除λ≠1的振動(dòng)傳遞模式而僅考慮行波解,則無法全面地描述有限長周期結(jié)構(gòu)的動(dòng)態(tài)特性。因此,下面將對非行波解的能量傳輸?shù)男蕟栴}做進(jìn)一步探討。
由縱波的討論可知,功率傳輸效率高低可以用輸入端所需的總能大小來衡量。對于周期桁架結(jié)構(gòu),其效率指標(biāo)η不妨定義為如下形式
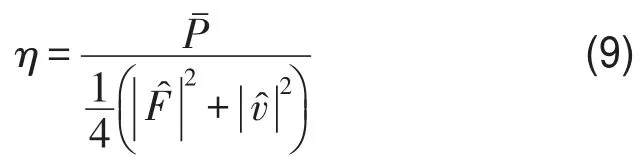
首先,根據(jù)式(3),注意到時(shí)均功率可表示為譜系數(shù)點(diǎn)乘的形式

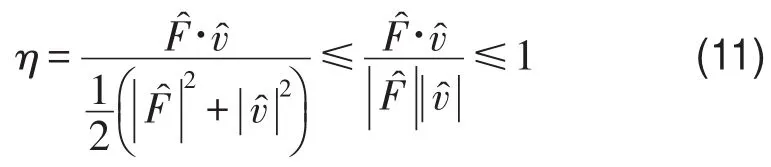
式(11)表明,按式(9)所定義效率指標(biāo)最大值不超過1(有上界),因此確實(shí)可以作為一種效率指標(biāo)。引入該指標(biāo)的好處是可以更全面地反映周期結(jié)構(gòu)能量傳輸特性。
對于非行波解,如果指定輸入/輸出端的振速幅值比λ及其相位差,則不同頻率下的效率值η將是個(gè)確定值,因此η是關(guān)于λ、Δφ和ω的三元函數(shù)

若固定λ,η函數(shù)可表示成一張二維曲面,稱為響應(yīng)表面;當(dāng)λ變化時(shí),將形成一系列曲面簇。利用響應(yīng)表面的局部極大值和極小值分布情況,就可以表征不同狀態(tài)下的能量傳輸效率。下面將針對有限周期桁架結(jié)構(gòu)的傳輸效率問題進(jìn)行仿真計(jì)算。
2 數(shù)值仿真
有限周期桁架計(jì)算模型如圖3所示。桁架類型為布朗型(Brown)。為了簡單起見,各桿件規(guī)格統(tǒng)一為:空心圓鋼管,外徑×壁厚=38 mm×3 mm。
在數(shù)值仿真中,輸入/輸出端采用位移激勵(lì),并假定截面位移是均勻的,所以邊界條件為
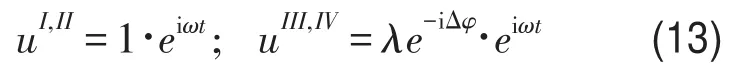
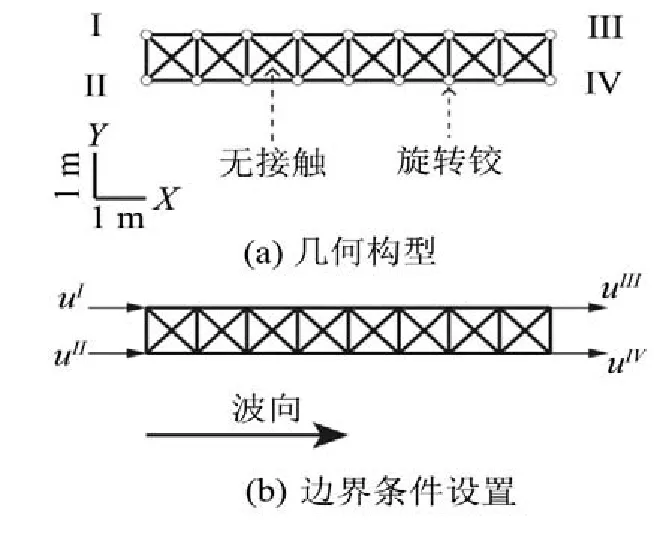
圖3 有限周期桁架計(jì)算模型
下面首先研究行波解的情況。
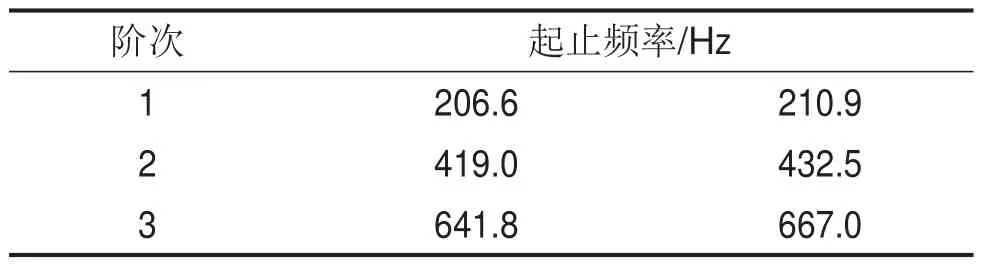
表1 桁架帶隙頻率
均勻媒質(zhì)中的縱波特性2表明行波解的功率因數(shù)為1,那么周期結(jié)構(gòu)中的行波解是否也存在上述特性?答案是肯定的,下面通過數(shù)值仿真的方式予以證明。
首先注意到行波解的λ=1,換句話說此時(shí)的功率因數(shù)cos?僅與輸入輸出端振速相位差Δφ和角頻率ω有關(guān),因此功率因數(shù)可視為關(guān)于頻率和輸入/輸出端相位差的二元函數(shù),在三維空間中可以繪制出一張曲面——功率因數(shù)響應(yīng)表面:。需要特別說明的是,該響應(yīng)表面給出λ=1時(shí)所有振動(dòng)傳遞模式的功率因數(shù)。將響應(yīng)表面的最大值(cos?=1)連線——形成所謂“脊線”,并向Δφ-ω平面投影,如果脊線的投影曲線與頻散曲線重合,則表明在λ=1的所有可能解中,僅有行波解能取到cos?=1。
為了證明這一點(diǎn),不妨用平面Δφ=φi作為橫截面,與功率因數(shù)響應(yīng)表面相交,所得橫截曲線如圖4 (b)所示。該曲線簇反映不同相位差下,功率因數(shù)隨頻率變化情況。對比圖4(a)和圖4(b)可知,給定輸入輸出端相位差Δφ,功率因數(shù)等于1的頻率恰好就是存在行波模式時(shí)的頻率。這就證明了在周期結(jié)構(gòu)中,僅有行波模式能夠以最大功率因數(shù)方式傳輸能量——與均勻媒質(zhì)中縱波特性2保持一致。上述現(xiàn)象也說明周期結(jié)構(gòu)中行波解的確是均勻媒質(zhì)中彈性波一種推廣。
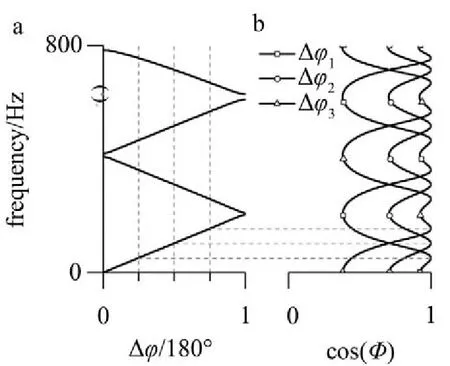
圖4 頻散曲線與功率因數(shù)之間的關(guān)系
對于有限長周期結(jié)構(gòu),其真實(shí)工作狀態(tài)下的(Δφ,ω )并不一定恰好落在頻散曲線上。因此,在圖4(a)所示的Δφ-ω平面上,還有大片空白區(qū)域的能量傳輸特性有待進(jìn)一步梳理。根據(jù)圖4所示的仿真結(jié)果,既然頻散曲線具有效率意義,若加以推廣,再將前述功率因數(shù)響應(yīng)表面上極大值、極小值相連,即可繪制出所謂“半高線”、“槽線”。根據(jù)脊線、半高線和槽線,可將Δφ-ω平面劃分為一系列能量傳輸高效區(qū)和低效區(qū)。下面將用效率指標(biāo)η代替cos?繪制上述各類曲線,其理由如下:
(1)效率指標(biāo)η綜合考慮了輸入端驅(qū)動(dòng)力和速度,能更全面地體現(xiàn)描述傳輸功率時(shí)所需建立的輸入端場能,特別在λ≠1情況下更有實(shí)際意義;
(2)對于均勻媒質(zhì)中的單列縱波,效率指標(biāo)η=1與功率因數(shù)cos?=1存在等價(jià)關(guān)系(根據(jù)縱波特性3),因此指標(biāo)η可以視為一種廣義的功率因數(shù)。
圖5(a)和圖5(b)的左半部分分別給出λ=1和λ=0.5時(shí),效率指標(biāo)η響應(yīng)表面的脊線、半高線、槽線在Δφ-ω平面上投影線;在右半圖中,特給出Δφ=90°時(shí)的η隨頻率變化曲線。在左半圖中,槽線的投影線恰為過fi(i=1…4)的水平坐標(biāo)線,故略去;fi(i=1…4)分別對應(yīng)前4階自由-自由邊界下的固有頻率:f1、f2、f3、f4分別為210 Hz、421 Hz、629 Hz和800 Hz。在右半圖中,特給出Δφ=90°時(shí)的η隨頻率變化曲線。
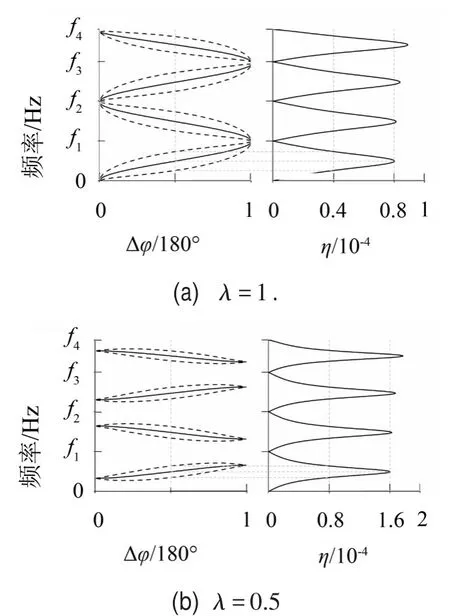
圖5 效率指標(biāo)η響應(yīng)表面的脊線(——)、半高線(––––)、槽線的投影線
3 討論
若輸入/輸出端振幅相同,在Δφ-ω平面上所繪制出的功率因數(shù)響應(yīng)表面的脊線,就是周期結(jié)構(gòu)行波解的頻散曲線。這意味著可以用效率指標(biāo)的等高線簇,將Δφ-ω平面劃分為能量傳輸高效區(qū)和低效區(qū)。其中能量傳輸?shù)托^(qū)意味著傳輸相同功率,需要在輸入端維持較高的能量水平,換句話,如果輸入端能量一定,該區(qū)域內(nèi)的振動(dòng)能量傳遞受到抑制。由此可見,效率觀點(diǎn)的引入,有助于將周期結(jié)構(gòu)帶隙理論拓展到非行波解范疇,為描述有限周期結(jié)構(gòu)的能量傳輸特性提供有力工具。
圖5(a)左半圖所示η函數(shù)的脊線,其形狀與如圖4(a)所示的頻散曲線相近:均為一條從原點(diǎn)出發(fā)的螺旋線(在圓柱面上一條螺旋線沿徑向投影可形成圖5(a)左半圖中的脊線),在脊線兩側(cè)分布有效率半高線。利用脊線與相鄰半高線就可確定某一頻率下,落在能量傳輸高效區(qū)時(shí)對應(yīng)的Δφ范圍。顯然,Δφ范圍越窄意味著對應(yīng)頻率的能量傳輸能力越差。例如,在圖5(b)左半圖中的灰色條形區(qū)域內(nèi),無論Δφ取任何值,都對應(yīng)能量傳輸?shù)托^(qū)。顯然,上述頻率范圍劃分方法與帶隙頻率確定方法是完全一致的。
對比圖5(a)和圖5(b)中的左半部分,不同振幅比λ下,脊線與半高線所圍面積有所不同,這反映了效率指標(biāo)η頻域曲線陡峭程度不同,這一點(diǎn)也可以從右半圖對比看出。對比圖5(a)和圖5(b)中右半部分所示的曲線峰值,可以發(fā)現(xiàn)λ=1時(shí),η的局部極大值均小于λ=0.5的情況。注意到行波模式屬于λ=1的情況,這說明對于有限周期結(jié)構(gòu),某些非行波解的能量傳輸效率反而要高于行波解,所以非行波模式對于有限周期結(jié)構(gòu)的能量傳輸貢獻(xiàn)不可忽視。
利用Δφ-ω平面上的η函數(shù)等高線族,可以對已有周期結(jié)構(gòu)隔振設(shè)計(jì)方案進(jìn)行評估,例如根據(jù)實(shí)際邊界條件,可計(jì)算出,從而確定其是否落在所期望的能量傳輸區(qū)域內(nèi);然而,根據(jù)上述等高線族,如何在輸出端確定合適的邊界阻抗參數(shù);或者根據(jù)已有邊界阻抗,如何設(shè)計(jì)合適的周期結(jié)構(gòu),都是下一步需要研究的。
4 方法
本文所涉及的仿真均在ANSYS軟件中實(shí)現(xiàn)。其中桁架的各桿單元類型為Link180。利用Harmonic模塊,獲得圖3(b)中的各邊界角點(diǎn)I~I(xiàn)V的幾何約束反力FI、…、FIV。針對不同Δφ,逐個(gè)計(jì)算節(jié)點(diǎn)力F的頻率響應(yīng),即可獲得一張二維數(shù)據(jù)表
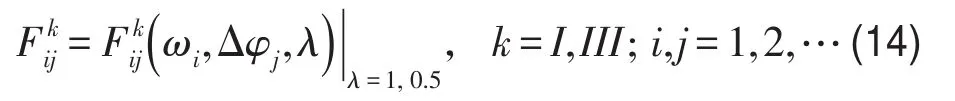
其中頻率步長為1 Hz,相位差Δφ步長為1°,范圍從1°~179°。利用輸入端的節(jié)點(diǎn)力即可方便地計(jì)算出功率因數(shù)cos?以及效率指標(biāo)η的響應(yīng)表面,從而在平面上繪制出有關(guān)曲線。
圖4(a)所示的頻散曲線按如下方式繪制:根據(jù)二維數(shù)據(jù)表Fij(i為行指標(biāo),j為列指標(biāo)),針對每一列數(shù)據(jù),查詢符合行波解判定式的行指標(biāo)i,從而確定一系列存在行波解的角頻率ω*;遍歷指標(biāo)j,重復(fù)上述查找過程,即可在平面上繪制出頻散曲線。圖5中的脊線、半高線的繪制方法類似,不再贅述。
5 結(jié)語
(1)周期結(jié)構(gòu)行波解對應(yīng)的頻散曲線可視為功率因數(shù)等于1的等高線。因此,頻散曲線具有功率傳輸效率意義。
(2)對于有限長周期結(jié)構(gòu),可以引入效率指標(biāo)函數(shù)η,用于刻畫一般振動(dòng)模式下(行波或非行波)的能量傳輸效率。利用η函數(shù)響應(yīng)表面的脊線、槽線和半高線,可以將頻率-波數(shù)平面劃分為一系列能量
[33] Suda Y, Nakadai S, Nakano K. Hybrid suspension system withskyhook control andenergy regenerationdevelopment of self- powered active suspension[J]. Vehicle System Dynamics, 1998, 29(S1):619-634.
[34]曹民,劉為,喻凡.車輛主動(dòng)懸架用電機(jī)作動(dòng)器的研制[J].機(jī)械工程學(xué)報(bào),2008,44(11):224-228.
[35] Li P, Zuo L, Lu J, et al. Electromagnetic regenerative suspension system for ground vehicles[C]//Systems, Man and Cybernetics (SMC), 2014 IEEE International Conferenceon. IEEE, 2014:2513-2518.
[36]王慶年,劉松山,王偉華,等.滾珠絲杠式饋能型減振器的結(jié)構(gòu)設(shè)計(jì)及參數(shù)匹配[J].吉林大學(xué)學(xué)報(bào)(工學(xué)版),2012,42(5):1100-1106.
[37]計(jì)民.汽車內(nèi)燃機(jī)原理[M].上海:同濟(jì)大學(xué)出版社,1997.
[38]朱智富.汽車廢熱利用的有效途徑[J].黑龍江工程學(xué)院學(xué)報(bào),2005,19(2):51-53.
[39]陳家瑞.汽車構(gòu)造[M].北京:機(jī)械工業(yè)出版社,2005.
[40] Hindi G, Zabeu C B, Langeani M. Turbocharged vs. turbocompounded ethanol engine:fuel- air equivalence ratio impact[R]. SAETechnical Paper, 2009.
[41]趙建云,朱冬生,周澤廣,等.溫差發(fā)電技術(shù)的研究進(jìn)展及現(xiàn)狀[J].電源技術(shù),2010,34(3):310-313.
[42]劉振全,肖尤明.轎車空調(diào)用單效溴化鋰吸收式冷熱水機(jī)組的探討[J].甘肅工業(yè)大學(xué)學(xué)報(bào),2001,27(1):56-58.
[43]吳寶志,金永康.汽車空調(diào)[M].北京:宇航出版社,1991.
[44]劉士軒.利用汽車?yán)鋮s廢熱驅(qū)動(dòng)的噴射式制冷裝置理論研究[D].長安大學(xué),2007.
[45](日)吉田佑作,祝玉文譯,用排氣渦輪發(fā)電機(jī)回收汽車發(fā)動(dòng)機(jī)廢熱[J].新能源,1989,(7):31-34.
[46]楊錫堯.余熱氫氣發(fā)生器-汽車環(huán)保、節(jié)能的關(guān)鍵技術(shù)[J].機(jī)械制造,2001,39(8):31-31.
[47]張立軍,李信中,劉熾棠.利用余熱改善柴油機(jī)燃用重油后的性能[J].小型內(nèi)燃機(jī),1997,26(5):1-4.
Study on the Band-gap of Periodic Structures in the Viewpoint of Power Efficiency
ZHOU Jun1, RAO Zhu-shi2, TA Na2
(1. Instituteof Vibration Shock & Noise, Shanghai Jiaotong University, Shanghai 200240, China; 2. StateKey Laboratory of Mechanical Systemand Vibration, Shanghai Jiaotong University, Shanghai 200240, China)
Abstract:Periodic structureistherepetitivein geometric configurationsor material properties, such astrussesand ribstiffened plates. In certain frequency bands, periodic structure can isolate the incident travelling waves. This property is widely applied in vibration isolator’s design. Generally, the analysis of periodic structure’s attenuation property is always based on infinite length assumption. It means that the periodic structure can extend infinitely in space. So, only travelling wave solutions have physical significance and the non- travelling wave solutions are neglected. However, the periodic structure in engineering is finite and the non-travelling wave solutions exist indeed. Therefore, the investigation of their power transfer propertiesisof significance. Thefiniteelement simulationsof theperiodic trussshow that thepower factor of the travelling wave solution is always equal to unity. It means that the dispersion curves are related to power transfer efficiency. Hence, the efficiency index function is introduced. According to the local maximum and minimum values of the index function’sresponsesurface, thefrequency-wavenumber spacecan bedivided into aseriesof high efficiency and low efficiency transfer regions. This method can be applied to both traveling and non-traveling wave solutions. The method extends the scope of band-gap analysis and gives an alternative approach for finite periodic structure’s power transfer analysis. Theresultsof thepresent work areof significancefor vibrationisolator’sdevelopment.
Key words:vibrationandwave; periodicstructure; power factor; efficiency; band-gap; truss
通訊作者:饒柱石,男,博士生導(dǎo)師。E-mail:zsrao@sjtu.edu.cn
基金項(xiàng)目:國家重點(diǎn)基礎(chǔ)研究發(fā)展計(jì)劃資助項(xiàng)目(2014CB046302)
作者簡介:2015-0-17 周俊(1983- ),男,上海市人,博士生,主要研究方向?yàn)榻Y(jié)構(gòu)波動(dòng)分析計(jì)算。
文章編號:1006-1355(2016)02-0001-05+45
中圖分類號:O328;TB535
文獻(xiàn)標(biāo)識碼:ADOI編碼:10.3969/j.issn.1006-1335.2016.02.001

