用于阻尼器的不同直徑NiTi絲力學性能試驗

黃　瑞，戴世群，鄭繼周，2( .山東農業大學機械與電子工程學院，山東泰安27000；2.山東省園藝機械與裝備重點實驗室，山東泰安27000)

?

用于阻尼器的不同直徑NiTi絲力學性能試驗

黃瑞1，戴世群1，鄭繼周1，2
( 1.山東農業大學機械與電子工程學院，山東泰安271000；2.山東省園藝機械與裝備重點實驗室，山東泰安271000)

摘要：通過對3種不同直徑NiTi形狀記憶合金絲進行多工況循環加載試驗，研究循環次數、應變幅值和加卸載速率對等效剛度、單循環耗能以及阻尼特性的影響。研究表明：經過多次加卸載循環進入穩定期后，形狀記憶合金絲的力學性能表現出良好的重復性。對于直徑相同的形狀記憶合金絲，等效剛度、單循環耗能和等效阻尼比都隨循環次數的增加而降低。隨著應變幅值的增大，等效剛度減小，而單循環耗能近似線性增加。研究結果對于開發形狀記憶合金被動阻尼元件具有指導意義。

關鍵詞：振動與波；形狀記憶合金；超彈性；性能試驗；力學性能

在眾多的功能材料中，形狀記憶合金（Shape Memory Alloy，SMA）具有兩個非常獨特的性質：形狀記憶效應和超彈性[1–4]。形狀記憶效應是指具有某種形狀的SMA制品，在變形以后可以通過加熱等方式使其恢復原始形狀。超彈性是指處于奧氏體狀態的SMA，當加載應力超過彈性極限后，繼續加載將發生由應力誘發的馬氏體相變；當應力去除后，伴隨著馬氏體逆相變，應變可以完全恢復。在加、卸載過程中，出現比較飽滿的遲滯環，使其具有較強的能量耗散能力[5]。此外，SMA還具有耐腐蝕、抗疲勞、可恢復變形大等優點，其可恢復應變高達6 %～8%，屈服應力在400 MPa～500 MPa左右，與鋼材相當；但其極限強度超過1 000 MPa，極限變形高達20 %。利用這些特性，可以制作SMA阻尼器，用于結構振動的被動控制。

國內外不少學者在SMA被動阻尼器的開發與應用方面進行研究。任文杰[6]建立基于SMA的X形板阻尼器的力學模型。彭剛[7]提出SMA阻尼器的阻尼特性分析及器件設計方法。錢輝[8]設計一種新型SMA阻尼器，并對其力學性能進行數值模擬。劉愛榮[9，10]進行新型SMA長拉索系統振動控制和斜拉橋振動控制研究。申文求[11]、肖爾田[12]、Graesser[13]和Feng[14]也對SMA絲減震器的應用做了相應研究。為了研制適用于工程結構的具有自復位功能的SMA阻尼器，錢輝[15]通過試驗考察三種直徑SMA絲力學性能。

在現有的文獻中，直接針對SMA減振器的研究居多，而對于SMA絲的力學性能關注較少。因此，在設計阻尼器時往往缺乏相應的參考資料。為了開發適用于小型精密機械的SMA阻尼器，對三種不同直徑的NiTi SMA絲進行了拉伸試驗，并研究了響其力學性能的一些關鍵因素，如循環加載次數、應變幅值、加載速率等。

1　NITi絲力學性能試驗

1.1試驗材料及設備

采用的NiTi SMA絲含Ni50.8 %、Ti 49.2 %，奧氏體相變結束溫度Af為5oC，即常溫下材料為奧氏體。試件有三種直徑，分別為0.5 mm、0.6 mm和0.8 mm。長度為150 mm，標距為100 mm。SMA絲的力學性能試驗在山東農業大學力學實驗室的JNT 150522型電液伺服動靜萬能試驗機上進行。該試驗機力傳感器量程為5 kN，加載速率范圍為0.1 mm/ min～500mm/min。

1.2試驗方案

試驗采用等速位移方式施加拉伸載荷。利用試驗機上的力傳感器和位移傳感器采集試件的負荷和位移，然后對采集的數據進行處理，以獲得所需要的應力-應變曲線。

1)等速率等幅值循環加載試驗，研究循環次數對SMA絲力學性能的影響。

加卸載速率為10 mm/min，應變幅值為5 %，每種直徑的SMA絲連續加卸載50個循環。

2)等速率變幅值循環加載試驗，研究應變幅值對SMA絲力學性能的影響。

加卸載速率為1 mm/min，應變幅值分別為4 %、5 %、6 %、7 %、8 %，每個幅值加卸載五個循環，一個幅值做完后緊接著進行下一幅值試驗，分析時只取每種幅值的最后一個循環。

3)等幅值變速率循環加載試驗，研究加載速率對SMA絲力學性能的影響。

應變幅值為5 %，加卸載速率分別為1 mm/min、5 mm/min、10 mm/min、15 mm/min、20 mm/min，每個速率加卸載5個循環，一種速率做完后緊接著進行下一速率試驗，分析時只取每種速率的最后一個循環。

1.3拉伸試驗結果

在加卸載速率為10 mm/min、應變幅值為5 %條件下，三種不同直徑SMA絲50次加卸載循環的應力-應變曲線如圖1所示。由于循環次數較多，圖中未對其一一標注。觀察發現，隨著循環次數的增加，SMA絲應力-應變曲線逐漸下移，其中第一循環由于內應力作用使其加卸載應力較大，隨循環次數的增加SMA絲內部組織趨于穩定，內應力逐漸降低，加之SMA絲長時間處于拉伸狀態,使其應力松弛，發生蠕變反應，致使加載所需的應力降低。在50次循環的中后期，應力-應變曲線變化的幅度逐漸減小，曲線越來越密，到最后幾乎重合。由于加載曲線下移明顯而卸載曲線變化較小，導致單循環加卸載曲線包圍的面積逐漸減小。

加卸載速率保持為1 mm/min，應變幅值分別為4 %、5 %、6 %、7 %和8 %時，三種直徑SMA絲的應力-應變曲線繪制于圖2中。由圖2可得，隨著應變幅值的增大，加載曲線經歷了三個階段：

1)應變幅值在0～1.5 %時為奧氏體彈性拉伸階段；

圖1　循環次數對應力應變的影響

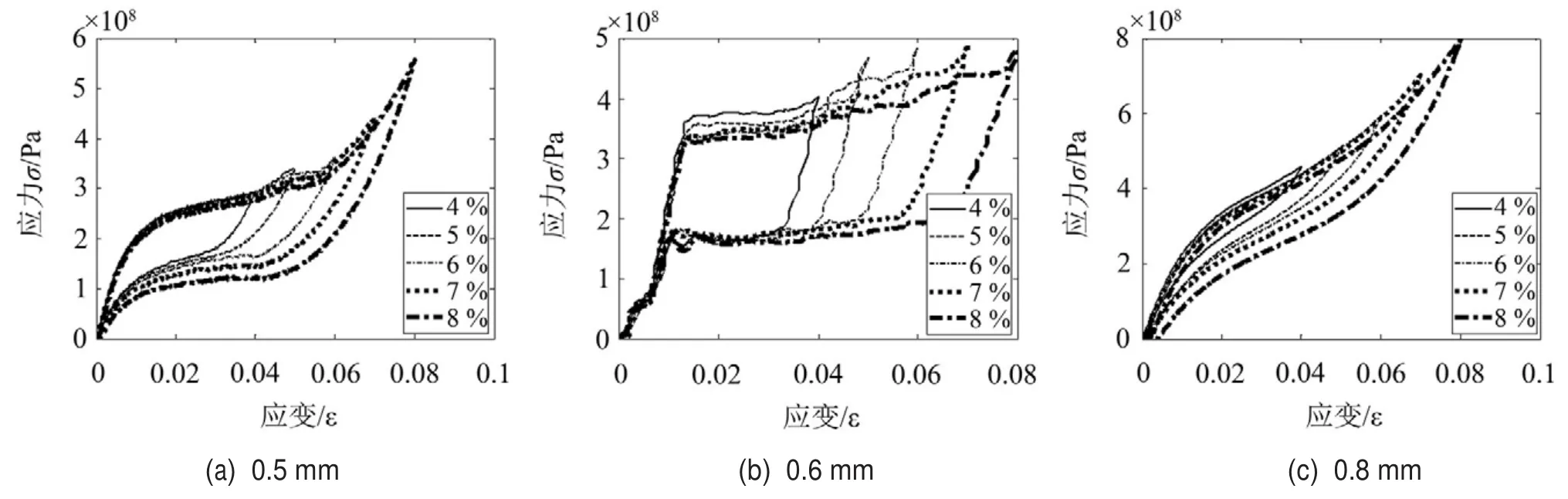
圖2　不同加載幅值時的應力-應變曲線

2)應變幅值在1.5%～6%時為奧氏體向馬氏體的轉變階段；

3)當應變幅值在6 %～8 %時為馬氏體彈性拉伸階段。

卸載曲線同樣經歷了三個階段分別為：

1)馬氏體彈性卸載階段。

2)馬氏體向奧氏體逆相變階段。

3)奧氏體彈性卸載階段。

由于各階段組織結構的不同導致SMA絲在不同應變幅值時的彈性模量不同。其中奧氏體和馬氏體彈性拉伸階段的彈性模量較大，奧氏體和馬氏體轉化過程的彈性模量較小。加卸載曲線所包圍的面積為SMA絲每循環所消耗的能量，同種直徑的SMA絲應變幅值越大，滯回曲線包圍的面積越大，耗能越多。

應變幅值為5 %，加卸載速率分別為1 mm/min、5 mm/min、10 mm/min、15 mm/min、20 mm/min時，三種直徑SMA絲的應力-應變曲線如圖3所示。由圖3可見，隨著加載速率的提高，加載應力均有所提高，這與材料的粘性變形特性緊密相關，當加載速率提高時會導致分子間的摩擦速率增加，分子間的滑動需要克服范德華力以及滑動摩擦力等，增加滑動速率必須增加應力以克服分子間的滑動阻力，因而要產生同樣的變形率需要較大的應力。

圖3　不同加載速率時的應力-應變曲線

2　SMA力學性能分析

為便于研究SMA絲力學性能，定義三個參數：等效剛度K、等效阻尼比ζ和每循環耗散能量WD，圖4為超彈性SMA絲的應力-應變示意圖。

1) WD為應變幅值為εδ時加卸載曲線包圍的面積，表征SMA每次循環的耗能能力；

2)等效剛度K為應力-應變曲線起點與終點連線的斜率，表達式為

3)等效阻尼比ζ表示SMA絲的阻尼能力，即SMA絲在單向拉伸然后卸載條件下的阻尼比。表達式為；其中WE為總應變能，

3種直徑SMA絲的力學特性隨循環次數的變化如圖5所示。可以看出，隨著循環次數的增加，SMA絲的等效剛度稍有下降，隨后基本保持不變。單循環耗能和等效阻尼比都隨循環次數的增加而降低，但20次循環前下降趨勢比較明顯，20次循環后下降趨勢逐漸放緩。因此，可以將20次循環作為一個分界點，將20次循環后稱為穩定期。

循環次數相同時，0.8 mm絲的等效剛度較大；0.5 mm絲的等效剛度最小，僅為前者的2/3左右；0.6mm絲的等效剛度基本相等，介于二者之間。

不同直徑SMA絲的單循環耗能差別較大，且單循環耗能隨循環次數的增加而降低，進入穩定期后下降趨勢變緩。0.6 mm絲的單循環耗能約為0.8 mm絲的三倍。

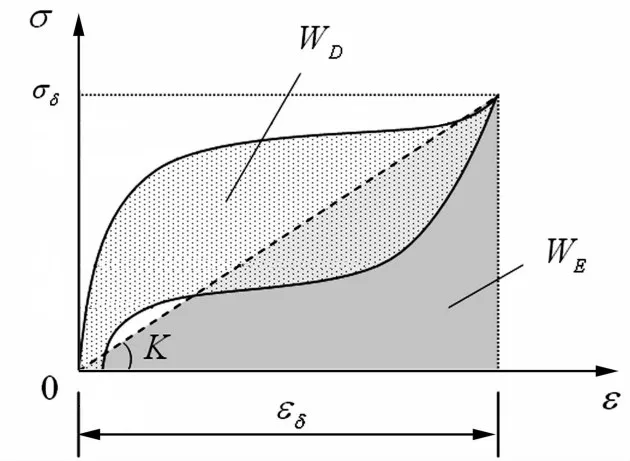
圖4　超彈性SMA絲的應力-應變示意圖

等效阻尼比的變化非常類似于單循環耗能。進入穩定期后，0.6 mm絲的等效阻尼比最大，0.8 mm絲的等效阻尼比最小，最大等效阻尼比約為最小等效阻尼比的三倍。

圖6為SMA絲在不同應變幅值時的力學特性曲線。由圖可見，隨著應變幅值的增大，等效剛度減小，而單循環耗能近似線性增加，二者呈現出較強的規律性。比較而言，等效阻尼比的變化幅度比較大。其中0.5 mm、0.6 mm絲的等效阻尼比先降后升，即在4 %和8 %兩個應變幅值附近出現兩個峰值，而應變幅值約為5 %時出現最小值。0.8 mm絲的等效阻尼比基本隨應變幅值增加而單調增加，在應變幅值8%附近達到最大。

不同加載速率時SMA絲的力學特性曲線繪于圖7中。可以看出，隨著加載速率的增大，等效剛度逐漸增大，加載速率從1 mm/min到20 mm/min每種直徑SMA絲的等效剛度增加均超過1 GPa。

隨著加載速率的增大，0.5 mm、0.6 mm和0.8 mm絲的耗能和等效阻尼比均呈現先增大后減小的趨勢，其中0.5 mm絲和0.8 mm絲在10 mm/min左右取得耗能和等效阻尼比的最大值，0.6 mm絲在6 mm/min左右取得耗能和等效阻尼比最大值。

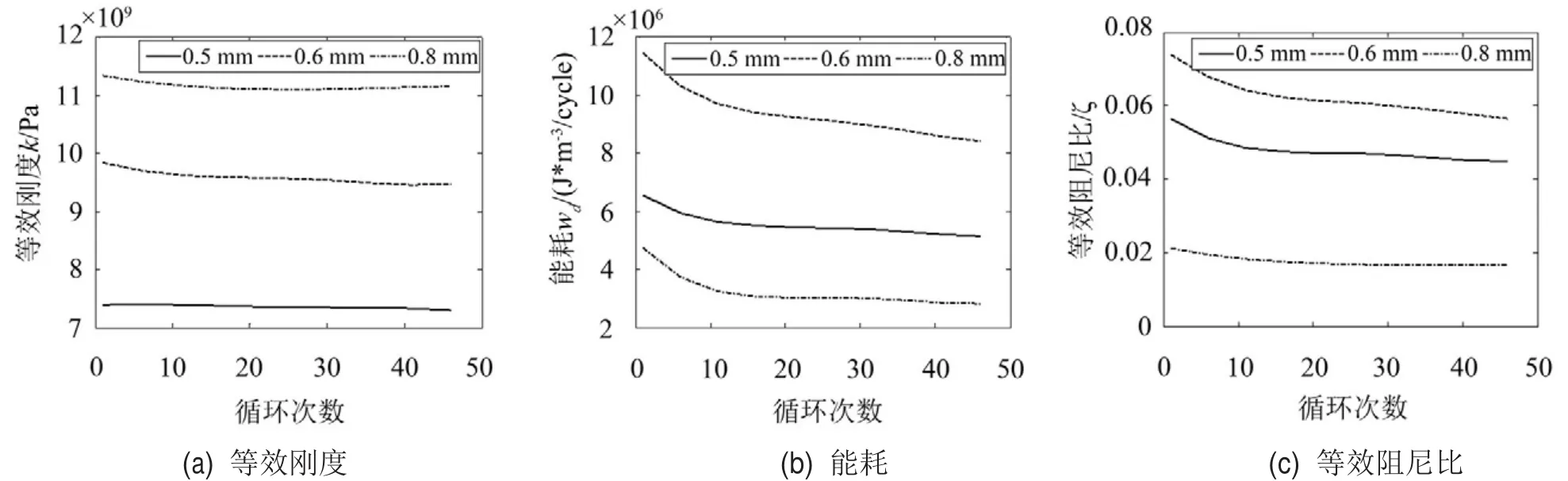
圖5　循環次數對SMA絲力學性能的影響

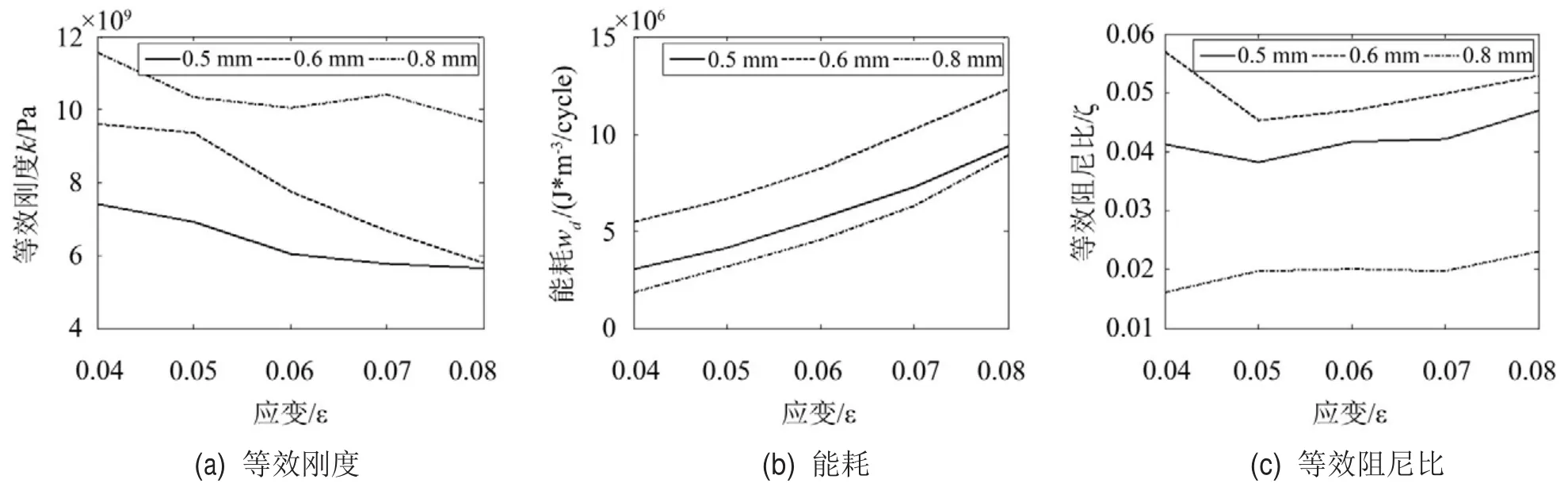
圖6　應變幅值對SMA絲力學性能的影響

3　結語

對0.5 mm、0.6 mm和0.8 mm的NiTi SMA絲進行了拉伸試驗，分析了不同直徑SMA絲的等效剛度、等效阻尼比和單循環耗能隨循環次數、應變幅值和加載速率的變化規律。最終可得出以下結論：

(1)經過20次左右應力循環后，SMA絲的力學性能趨于穩定，表現出良好的力學性能重復性。

(2)適當增大應變幅值和加卸載速率能夠提高SMA絲的阻尼性能。

(3)隨著循環次數的增加，相同直徑SMA絲的等效剛度、單循環耗能和等效阻尼比都降低。

(4)隨著應變幅值的增大，相同直徑SMA絲的等效剛度減小，而耗能近似線性增加。

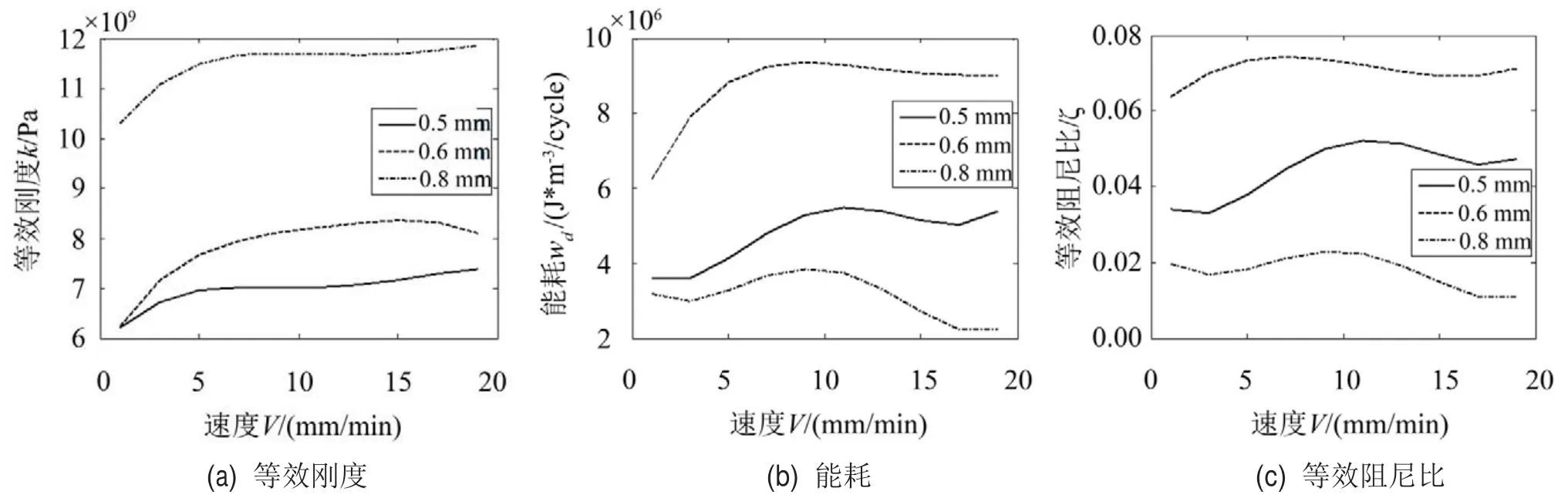
圖7　速度對SMA絲力學性能的影響

參考文獻：

[1]董軍輝，薛素鐸.形狀記憶合金在結構振動控制中的應用[J].世界地震工程，2002，18(3)：123-129.

[2]張新平，張宇鵬.多孔NiTi形狀記憶合金研究進展[J].材料研究學報，2007，21(6)：561-567.

[3]錢輝，李宏男，任文杰，等.形狀記憶合金復合摩擦阻尼器的設計及試驗研究[J].建筑結構學報，2011，32(9)：58-64.

[4]李惠，毛晨曦.新型SMA耗能器及結構地震反應控制試驗研究[J].地震工程與工程振動，2003，23(1)：133-139.

[5]鄭繼周，張艷.形狀記憶合金超彈性分段線性模型及其阻尼特性[J].振動與沖擊，2102，31(3)：136-140.

[6]任文杰，李宏男，宋鋼兵.基于形狀記憶合金的X形板阻尼器的力學模型[J].振動與沖擊，2006，25(4)：53-57.

[7]彭剛，李黎，唐家祥. SMA阻尼器的阻尼特性分析及器件設計方法[J].固體力學學報，2003，24(1)：109-112.

[8]錢輝，李宏男.形狀記憶合金阻尼器消能減震體系的控制研究[J].振動與沖擊，2008，27(8)：42-47.

[9]劉愛榮，禹奇才.基于新型SMA粘滯阻尼器的斜拉橋振動控制研究[J].廣州大學學報，2009，8(4)：75-77.

[10]劉愛榮，禹奇才，袁向榮，等.基于SMA阻尼器的長拉索系統振動控制研究[J].中山大學學報，2009，48(1)：98-102.

[11]申文求，韓玉林，孫志林，等.基于一種新型形狀記憶合金阻尼器的索振動控制研究[J].中國機械工程，2009，20(2)：167-170.

[12]肖爾田，韓玉林，李愛群，等.基于形狀記憶合金超彈性阻尼器的結構振動控制和地震時程分析[J].東南大學學報，2003，33(5)：605-609.

[13] Graesser E J , Gozzarell F A. Shape memory alloys as new materials for seismic isolation[J]. Journal of Engineering Mechanics, 1991, 117(11):2590-2608.

[14] Feng Z C , Li D Z . Dynamics of a mechanical system with a shape memory alloy bar[J]. Journal of Intelligent Materials and Structures, 1998, 7:399-410.

[15]錢輝，李靜斌，李宏男，等.結構振動控制的不同直徑NiTi絲力學性能試驗研究[J].振動與沖擊，2013，32 (24)：89-95.

[16]趙亞哥白，佴磊，毛晨曦.用于阻尼器結構不銹鋼絲金屬橡膠元件力學性能試驗研究[J].震災防御技術，2010，5 (3)：370-376.

Mechanical Property Tests of NiTi Wires with Different Diameters Used for Dampers

HUANG Rui1, DAI Shi-qun1, ZHENG Ji-zhou1, 2
（1. Collegeof Mechanical and Electronic Engineering, ShandongAgricultural University, Tai’an 271000, Shandong China; 2. Shandong Provincial Key Laboratory of Horticultural Machinery and Equipment, Tai’an 271000, Shandong China）

Abstract:Cyclic loading tests of SMA wires with different diameters were conducted in various conditions, and the influenceof cyclic number, strain amplitudeand loading frequency on equivalent stiffness, energy dissipation per cycle, and damping properties was investigated. The results show that the mechanical behavior of the SMA wires manifests a good repeatability after the wires entering into a stable period through numerous cycles. For the SMA wires with the same diameter, the equivalent stiffness, energy dissipation per cycle, and the equivalent damping ratio decrease with the increase of cyclic times. With thestrain amplitudeincreasing, theequivalent stiffnessdecreaseswhiletheenergy-absorption increases linearly. Theresultshaveanintroductivesignificanceinthedevelopment of dampingelements.

Key words:vibrationandwave; shapememory alloy(SMA); super elasticity; performancetesting; mechanical behavior

通訊作者：戴世群（1991-），男，山東省莒縣人，碩士生，主要研究方向為噪聲與振動控制。 鄭繼周，男，碩士生導師。E-mail:zjzcorlor@163.com

作者簡介：黃瑞（1990-），男，山東省東阿縣人，碩士生，主要研究方向為形狀記憶合金金屬橡膠的工藝流程和性能試驗研究。

基金項目：山東省優秀中青年科學家科研獎勵基金資助項目（BS2010ZZ010）

收稿日期：2015-07-07

文章編號：1006-1355(2016)02-0189-05

中圖分類號：TB535+.1；TB34

文獻標識碼:ADOI編碼：10.3969/j.issn.1006-1335.2016.02.042