不規則結構導納參數建模方法研究

張武林，盛美萍（.西北工業大學航海學院，西安70072；2中國飛行試驗研究院飛機所，西安70089）

?

不規則結構導納參數建模方法研究

張武林1, 2，盛美萍1
（1.西北工業大學航海學院，西安710072；2中國飛行試驗研究院飛機所，西安710089）

摘要：復雜結構都是由各種不規則子結構組成，一般采用動力學試驗或者仿真分析方法獲得其振動特性。而為了快速獲取復雜結構振動響應規律，指導結構聲學設計，常需開展子結構參數化建模。導納反映了結構振動響應特性。以導納作為等效建模基本參數，對發動機中泵結構建立矩形空心梁等效模型，通過改變激勵位置及材料參數，并結合試驗測試結果，證明所建立模型的正確性及建模方法的適用性。

關鍵詞：振動與波；導納；參數化建模；子結構

組合結構都是由各子結構通過一定的耦合方式連接而成。分析各子結構的振動特性以及子結構之間的耦合特性，將有助于研究子結構間的振動傳遞特性，在此基礎上獲取振動傳遞規律，還將對結構的聲學設計具有一定的指導意義。

開展結構的導納參數建模，可以有效地預估結構在任意激勵下的振動響應，并且基于參數化模型可以實現復雜結構振動傳遞的最優化設計。目前，參數化建模已在典型結構如梁、板、殼及其耦合結構上得到了廣泛應用[1–3]，而復雜結構如何建立合理有效的等效參數化模型，及不同激勵條件下各結構參數變化對耦合模型振動傳遞特性有何影響，對于此類問題的研究相對較少。對于實際中的子結構，多數已不再是傳統意義上的典型結構，同時還存在著與其相連子結構之間的復雜耦合作用，能否對其進行準確的參數建模將會對獲取結構振動傳遞特性產生非常重要的影響。以發動機中的泵結構為研究對象，討論不規則結構的導納參數模型的建模方法，以期能夠將該建模方法應用于解決工程實際問題。

在提出建模方法之前，首先對文中所用到的相關理論知識做一簡單介紹。

1　相關理論

對于端點受簡諧激勵的彎曲振動梁，可以將激勵載荷作為邊界條件推導梁的強迫振動響應，當激勵載荷作用于梁上任意一點時，可以將梁在激勵位置處一分為二，如圖1所示，在激勵位置處聯立位移、轉角、剪力、彎矩等連續條件，計算獲得其振動特性。

設彎曲振動梁的空間分布形式為[4, 5]

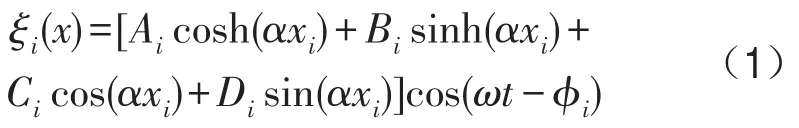
其中i=1，2，分別對應于梁1與梁2。

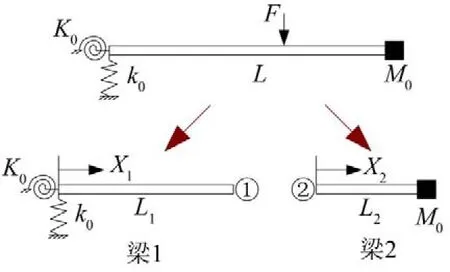
圖1　一端彈性、一端約束附有集中質量的中間受激彈性梁

梁1左端邊界條件與梁2右端邊界條件分別為

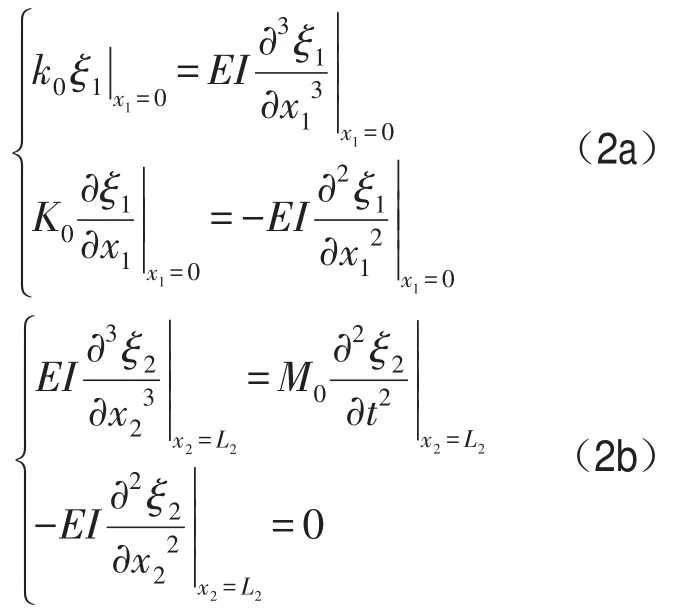
在梁1與梁2連接位置處，位移相等，轉角相等，彎矩相等，剪力之差等于外載荷，即

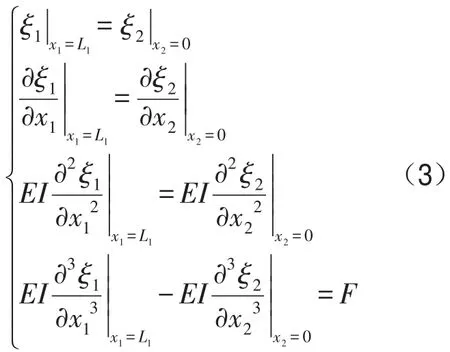
當梁中間受到彎矩激勵時，可以得到類似于式（3）的關系式。聯立上述的邊界條件，就可以得到梁上任意一點處的結構振動響應。

分段梁模型的處理方法，將激勵載荷作為分界點處的連續條件，很好地將梁彎曲振型的推導方法應用于任意位置點激勵下彎曲振動響應的計算，為梁的受迫振動分析提供了一個簡單直接的計算方法。

2　泵結構振動特性分析

泵結構為發動機的主要動力源結構，由螺栓連接于發動機上，主要用于汲取外部燃料以滿足發動機工作需要。泵頂端及底端安裝法蘭為近似矩形，中間部分外輪廓為不規則多邊形，而其內部則為沿泵軸向的活塞空腔，泵橫截面示意圖如圖2所示，圖中虛線表示頂端與安裝法蘭截面，泵高度h=20.0 cm。分析其結構特點可以看出，該泵為不規則結構。

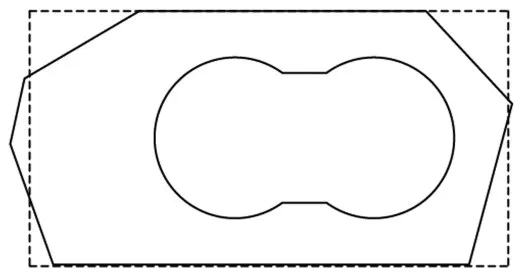
圖2　泵結構截面示意圖

對于非規則結構，無法直接從理論上獲取其振動特性。泵結構尺寸相對較小，結構剛度較大，在研究頻率范圍內（200 Hz～3000 Hz），自由邊界條件下無振動模態，不易激起結構的振動響應，不利于開展結構的導納參數建模；而在發動機正常工作情況下，泵通過四角處的螺栓將其固定于發動機的前隔板上，為保證工作時的穩定性及安全性，此安裝剛度較大，故這里首先借助有限元對固支邊界條件下的泵結構進行振動特性分析，計算得到泵的前兩階振型如圖3所示，各階固有頻率及對應振型描述見表1。

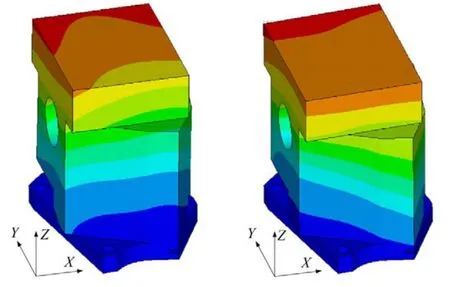
圖3　固支邊界下泵的前兩階振型

表1　固有頻率與對應振型描述

泵受到的主要激勵載荷是入口處作用于殼體的徑向激勵力[6]，圖3中結構左側圓形缺口即為泵的入口。仿真計算得到入口處點力激勵下的輸入導納如圖4所示。

由圖4可以看出，在研究的頻率范圍內，泵共有兩階模態峰值，第1階峰值較大，其對應振型平行于激勵方向；第2階振型與第1階近似正交，在所研究激勵下，對輸入導納的貢獻較小；所以在對泵等效參數建模時，應主要考慮第1階振型。

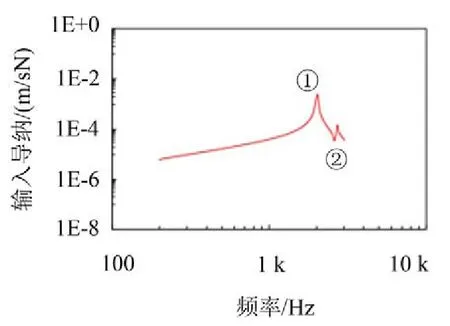
圖4　入口點力激勵下的輸入導納

3　泵導納參數模型的建立與驗證

由上述分析結果可知，第1階峰值對泵及泵與發動機的耦合結構的振動特性起主要作用，而第1階峰值所在頻段內輸入導納的變化特性與梁的彎曲振動相似，故可以考慮采用梁模型對泵進行導納參數建模。

泵為非規則結構，等效為梁模型時，其部分參數的確定是一個復雜過程。觀察其結構特點，寬度（垂直激勵方向）與厚度（平行激勵方向）的比值接近2:1，且為中空結構，聯系其振型特點，可以考慮將泵等效為矩形空心梁模型，取空心梁截面的外尺寸與泵的外尺寸近似相等，其余等效參數的獲取流程如圖5所示。

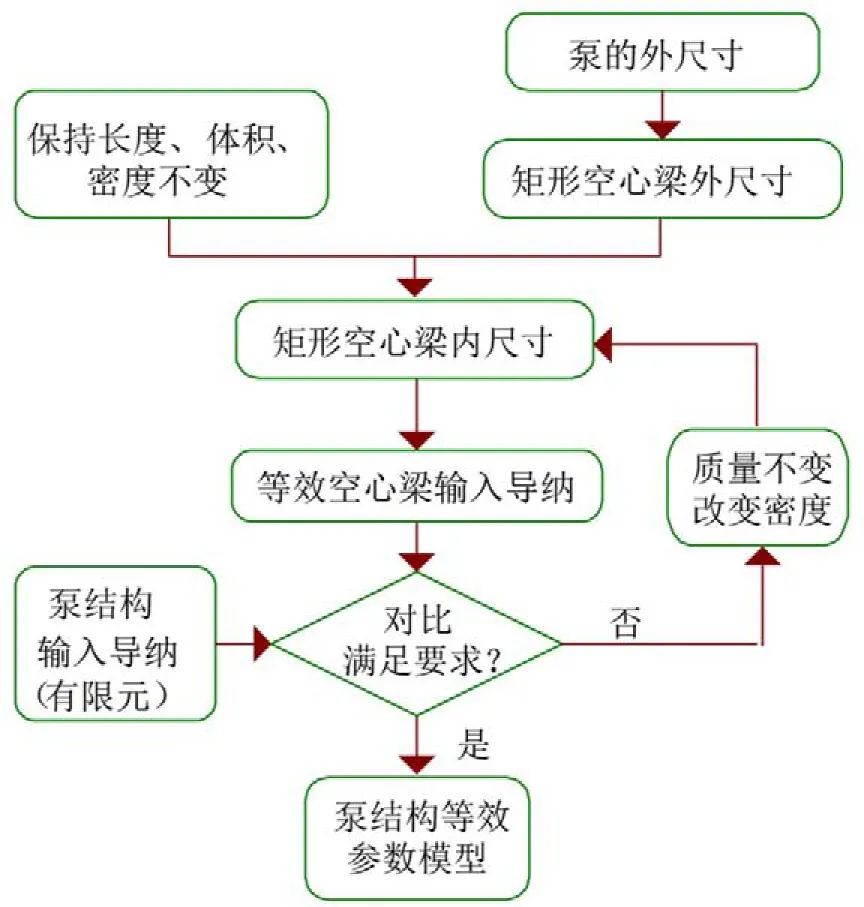
圖5　矩形空心梁等效參數的獲取流程

基于上述方法第一次得到的空心梁內尺寸計算泵的輸入導納時，所得結果會有一定誤差，可對內尺寸多次修正，得到最佳等效模型，在對內尺寸修正時，需保證泵的質量不變，即密度除以體積變化倍數，基于所得參數計算獲取等效梁模型的輸入導納如圖6所示。

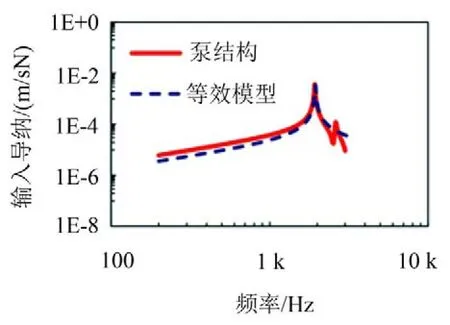
圖6　等效模型與泵結構輸入導納對比

由圖6可以看出，等效模型在研究頻段內具有較好的近似效果；同時，對于該等效模型，其正交方向上彎曲振動的第1階固有頻率為2736 Hz，與有限元仿真結果2684 Hz的誤差不足2%，等效模型近似程度較高，所以當泵所受的激勵載荷方向發生偏移時，只需將激勵載荷正交分解，直接采用矩形空心梁進行導納計算，無需再次等效。

子結構的導納參數化建模是指當原結構參數發生變化時，只需改變等效模型對應參數，即可近似獲取原結構導納特性的一種建模方法。

依次改變等效模型的載荷激勵位置（距離安裝底面14.2m→7.5cm）、彈性模量（70 GPa→97 GPa）、材料密度（2700kg/m3→4000kg/m3），計算獲取導納參數模型的輸入導納，并與有限元計算結果進行對比，如圖7至圖9所示。

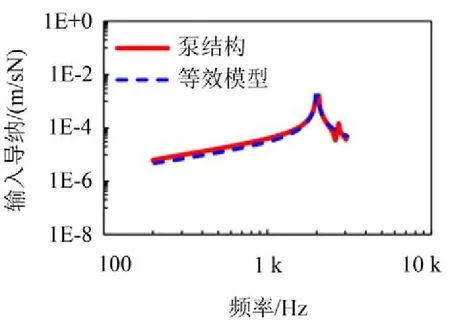
圖7　改變載荷激勵位置后輸入導納對比

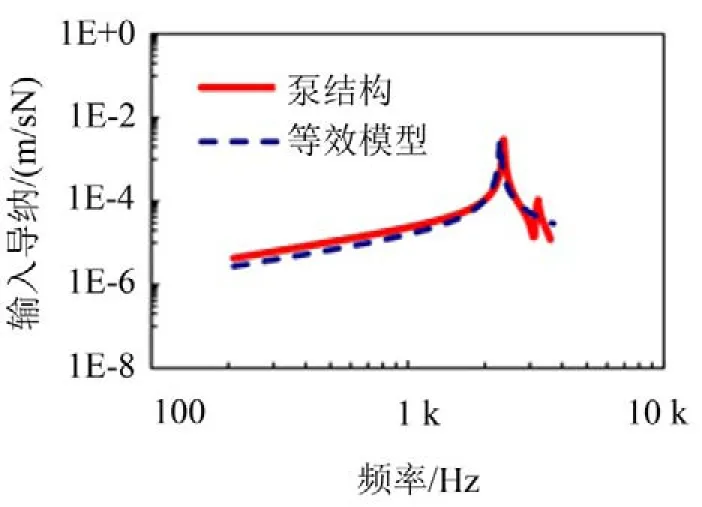
圖8　改變彈性模量后輸入導納對比

兩個激勵位置位于入口周邊，距離安裝底面最遠與最近處，而變化后的材料參數則取自發動機其他子結構的材料參數。分析各圖可以看出，激勵位置變化只影響峰值大小，彈性模量變大，固有頻率上移，材料密度變大，固有頻率下移；當在小范圍內改變上述參數時，所建立的導納參數模型在所研究頻段內仍具有較好的等效效果。

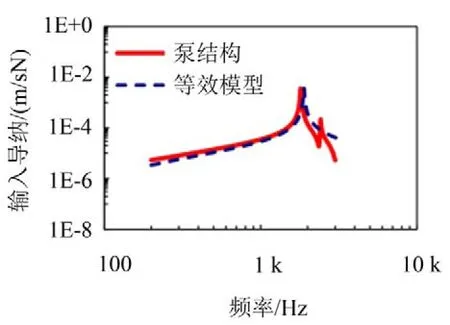
圖9　改變材料密度后輸入導納對比

4　耦合模型建立與驗證

發動機圓隔板在(r1,θ1)與泵結構耦合，泵受到F0的作用，其垂直于泵的軸向且沿隔板徑向，隔板受到軸向力F2作用，子結構與圓隔板耦合模型示意圖如圖10所示。

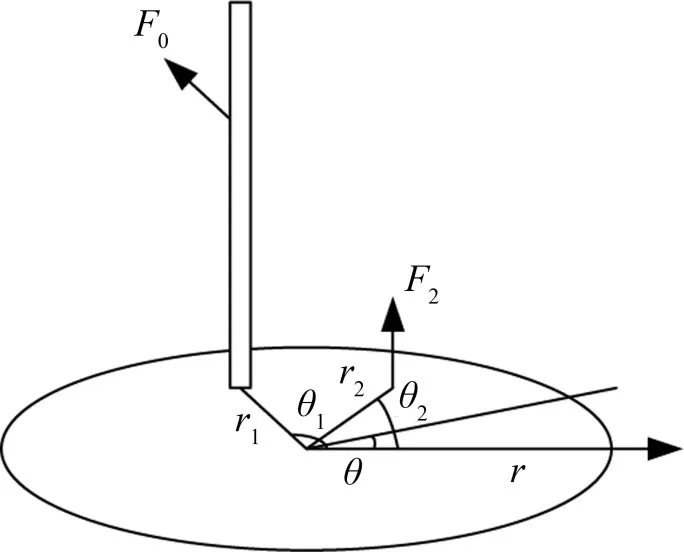
圖10　子結構與隔板耦合示意圖

在以梁的彎曲振動為主要考慮對象的梁板耦合系統中，耦合彎矩為主要耦合作用力（已由有限元模型驗證），下面基于此討論子結構與隔板耦合系統的導納計算方法。由子結構導納法，可以得到梁與圓板在耦合點處的角速度

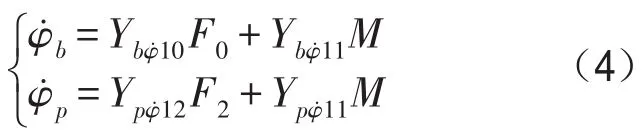
式中角標b對應于梁，角標p對應于隔板，角標0對應于梁上激勵點，角標2對應于圓板上激勵點，角標1對應于梁與圓板的耦合點，M對應于耦合彎矩，Y對應于梁與隔板的傳遞導納。

在連接位置處，子結構邊界保持連續[7]，對于梁與圓板耦合連接，在耦合位置處角速度相等，即，由式（4）進一步可以得到耦合彎矩

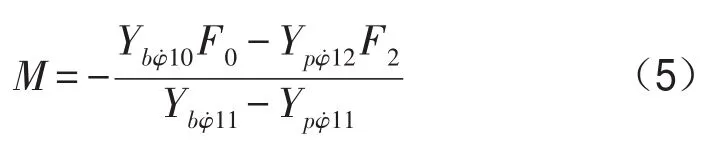
求解出耦合彎矩后，就可以得到梁上任一點處的速度響應

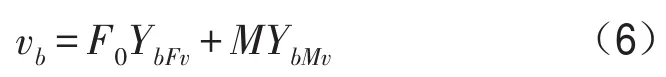
圓板上任一點處的速度響應

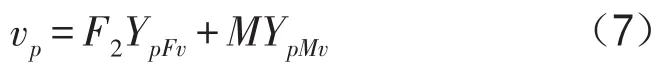
對于由多個子結構連接形成的耦合模型，采用上述計算方法，可以得到耦合矩陣方程

其中Y表示各子結構傳遞導納形成的導納矩陣，F表示耦合載荷矩陣，V表示外載荷引起的對應子結構的響應矩陣。

將矩形空心梁與發動機的導納參數模型耦合連接，計算得到耦合模型的輸入導納，并與試驗測試結果對比，如圖11所示。

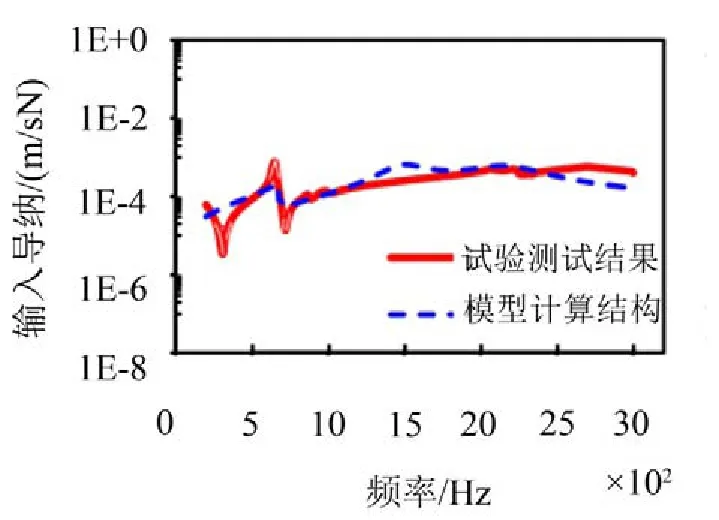
圖11　耦合結構輸入導納對比

由圖11可以看出，理論計算值與試驗測試值變化趨勢保持一致，除部分頻點外，二者差值較小。

經過上述對獨立子結構模型以及耦合模型的驗證可知，在研究頻率范圍內，導納參數模型具有較高的等效精度，進一步證實了該建模方法的有效性與正確性。當改變耦合模型中任一子結構的參數時，基于耦合模型的導納參數化模型，可以快速計算得到模型的振動傳遞規律以及子結構參數對耦合模型上目標位置處振動響應的影響特性，所以，建立組合結構的導納參數模型為耦合結構振動特性的獲取及結構的聲學優化設計奠定了基礎。

5　結語

(1)以發動機中的泵結構為研究對象，探索了非規則結構導納參數模型的建模方法，通過改變結構的激勵位置及材料參數，并對比有限元計算結果，證明了該建模方法的可行性及所建立導納參數模型的正確性。

(2)該方法已成功地運用于獲取發動機其他子結構的導納參數模型；導納參數模型的建立，將慢而復雜的有限元計算轉化為耦合結構的導納參數計算，大大簡化了振動傳遞的計算過程。

傳輸高效區和低效區。該劃分方式對行波解和非行波解均有效，可以全面地刻畫有限長周期結構的能量傳輸特性。

(3)在某些情況下，非行波解的能量傳輸效率可以高于行波解，換句話說，在有限周期結構中，傳輸效率最高的模式未必是行波模式，因此在應用周期結構原理設計隔振器時，需要考慮非行波模式對能量傳輸的貢獻。

參考文獻：

[1] Brillouin L. Wave propagation in periodic structures:electric filters and crystal lattices. secord edition[M]. New York:Dover Publications, 1953.

[2]吳代鳴.固體物理基礎第2版[M].北京：高等教育出版社，2015.

[3] Mead D J. Wave propagation in continuous periodic structures:Research contributions from Southampton, 1964-1995［J］. Journal of Sound and Vibration, 1996, 190(3):495-524.

[4]陳斌，黃修長.周期結構振動控制研究現狀[J].噪聲與振動控制，2011，31(5)：37-41.

[5] Hussein, M I, Leamy M J, Ruzzene M. Dynamics of phononic materials and structures:historical origins, recent progress, and future outlook[J]. Applied Mechanics Reviews, 2014, 66(4):040802.

[6] Bondaryk J E. Vibration of truss structures[J]. Journal of the Acoustical Society of America, 1997,102(4):2167-2175.

[7]黃修長，徐時吟，華宏星，等.梁周期結構動力學特性和隔振性能[J].上海交通大學學報，2013，47(2)：173-179.

[8] Xiao Y, Wen J, Yu D, et al. Flexural wave propagation in beams with periodically attached vibration absorbers:Band- gap behavior and band formation mechanisms[J]. Journal of Sound and Vibration, 2013, 332(4):867-893.

[9]尹劍飛，溫激鴻，肖勇，等.基于高級統計能量分析的周期加筋板振動特性研究[J].物理學報，2015，(13)：182-191.

[10] Mei J, Ma G C, Yang M, et al. Dark acoustic metamaterials as super absorbers for low-frequency sound [J]. Nature Communications, 2012, 3(2):132-136.

[11] Yan Y, Cheng Z, Menq F, et al. Three dimensional periodic foundations for base seismic isolation[J]. Smart Materials & Structures, 2015, 24(7):075006.

[12] Wang P, Casadei F, Shan S C, et al. Harnessing buckling to design tunable locally resonant acoustic metamaterials [J]. Physical Review Letters, 2014, 113(1):014301.

[13]溫激鴻，王剛，郁殿龍，等.聲子晶體振動帶隙及減振特性研究[J].中國科學：E輯，2007，37(9)：1126-1139.

[14]劉啟能，劉沁.固-固有限周期聲子晶體中SH波全反射隧穿的機理[J].計算力學學報，2014，31(1)：61-66.

[15]臧獻國，于德介，姚凌云.響應表面法在結構噪聲優化中的應用研究[J].噪聲與振動控制，2009，29(4)：116-119.

[16] Mead D J. A general theory of harmonic wave propagation in linear periodic systems with multiple coupling[J]. Journal of Sound and Vibration, 1973, 27 (2):235-260.

Study on Mobility Parametric Modeling of Irregular Structures

ZHANG Wu-lin1, 2, SHENG Mei-ping1
( 1. School of MarineScienceand Technology, Northwestern Polytechnical University, Xi’an 710072, China; 2.Aircraft Research Institute, ChinaFlight Test Establishment, Xi’an 710089, China)

Abstract:Complex structuresconsist of variousirregular sub-structures. Their vibration characteristicscan usually be obtained by dynamic test and simulation analysis. In order to quickly obtain thevibration responseof thecomplex structures and guide acoustic design of the structures, parametric modeling of sub-structures is necessary. In this paper, the mobility, which can reflect thestructural vibration responsecharacteristics, wasused asthebasic parameter to build an equivalent boxbeam model of engine pumps. By changing the excitation position and material parameters and combining with the test results, thecorrectnessandapplicability of theparametricmodel wereverified

Key words:vibrationandwave; mobility; parametricmodeling; sub-structure

作者簡介：張武林（1987-），男，河南省商丘市人，助理工程師，主要研究方向為噪聲與振動測試及其控制。E-mail:595172061@qq.com

收稿日期：2015-09-09

文章編號：1006-1355(2016)02-0027-04+45

中圖分類號：TB123

文獻標識碼：ADOI編碼：10.3969/j.issn.1006-1335.2016.02.006