先進戰機大迎角機動仿真研究

張佳龍, 姚宏, 姜久龍

(1.空軍工程大學 航空航天工程學院, 陜西 西安 710038;2.空軍工程大學 理學院, 陜西 西安 710051)

?

先進戰機大迎角機動仿真研究

張佳龍1, 姚宏2, 姜久龍1

(1.空軍工程大學 航空航天工程學院, 陜西 西安 710038;2.空軍工程大學 理學院, 陜西 西安 710051)

摘要:考慮戰機非線性運動建模中推力矢量、非定常氣動力等因素,建立了適合戰機大迎角機動縱向動力學模型和非定常氣動力模型,采用數值仿真對速度、平尾偏角、推力矢量舵偏角及俯仰角速度動態特性進行了分析?；谀承蛻饳C大迎角機動的仿真結果表明:各參數的變化符合實際情況,能夠有效地反映真實機動狀態,為大迎角機動飛行操穩系統的設計提供了依據。

關鍵詞:大迎角機動; 仿真分析; 非定常氣動力; 操穩系統

0引言

高性能戰機在進行大迎角過失速飛行時,采用可控的戰術機動飛行,可以實現先敵瞄準、獲得位置優勢,同時還有較強的航跡變向能力[1],在近距離空戰中占有絕對優勢,尤其在大迎角機動飛行中能夠使得戰機迅速定位并指向開火,從而極大地提高了作戰效能。但是現代戰機在大迎角機動時,機動的強耦合使得戰機的機動變化和操控性變得異常復雜。

為使戰機具備過失速機動能力[2],需要提高大迎角條件下飛行的操縱效率。當戰機處于大迎角狀態時,其氣動的非線性、不對稱性、交叉耦合及遲滯特性[3]都使得戰機處于非平穩狀態、動態特性降低、操控性降低及穩定性變差,同時會出現如機翼搖晃、上仰、過失速等情況,此時迎角的微小變化,就可能引起飛行參數的很大變化,甚至會使戰機從動穩定變為動不穩定[4],導致戰機振動失穩,釀成飛行事故。

在大迎角狀態的非定常氣動力建模中,設計人員提出了許多大迎角非定常氣動力建模方法,如Fourier函數建模方法[5]、多項式建模方法、積分和微分方程建模方法[6]、模糊邏輯建模[7]等。在此基礎上,通過參數辨識得到一個確定的氣動力模型,避免了多項式模型人為設定影響、模糊等智能方法帶來的物理意義不明確的問題[8]。

本文提出了在大迎角機動過程中,針對速度限制引起戰機因失速導致的失穩問題,分析了具有推力矢量戰機大機動階段空氣動力學機理,建立了戰機大迎角機動縱向動力學模型和非定常氣動力數學模型,并對戰機的空戰大機動進行了仿真驗證,為大迎角階段飛行品質的改善提供了理論依據。

1大機動機理分析

1.1非定常氣動力分析

在大機動飛行過程中,隨著速度不斷增大,迎角也逐漸增大。當增大到失速迎角時,繞戰機的氣流將在戰機背風面產生強烈漩渦和分離流動[9]。漩渦和分離流動使得戰機的升力損失程度不同,兩翼的升力不等,進而產生滾轉。通過風洞試驗可以測出大迎角機動過程中氣動力、氣動力矩等參數。在大機動動態過程變化中,戰機表面的氣流分離、漩渦生成與破碎的過程將由于動態效應變得非常復雜[9]。戰機漩渦流動分離如圖1所示。

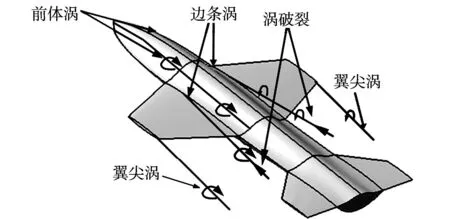
圖1　漩渦主導戰機大迎角流動分離Fig.1　Separation of vortex flow in the high AOA attack maneuver of aircraft

在小迎角飛行時,戰機氣流沒有分離,氣動力響應可以分解為靜態氣動力分量與由定常旋轉和下洗遲滯等產生的氣動力增加之和。在大迎角飛行時流動發生分離,形成一個或多個渦系。隨著迎角的增加,渦結構穩定性喪失,直至在尾中破裂,破裂點由尾跡向翼尖移動;當迎角減小時,破裂點反向運動。流動顯示表明,在非定常運動中,迎角增加時渦的破裂和迎角減小時渦的恢復存在滯后反向運動，從而產生氣動力的附加值。側滑角的存在使得左、右渦破裂位置點不對稱,其變化也將導致左、右渦破裂點位置非定常變化,從而產生非定常氣動力。此時,定常旋轉和下洗遲滯等因素依然存在,但是其影響比渦破裂點本身的非定常效應小得多[10]。因此,氣動力由三部分組成:靜態氣動力分量,以及由定常旋轉和下洗遲滯產生的氣動力。因而,在大機動過程中,受氣流影響,戰機操穩性是很難控制的。

1.2動力學分析

在大迎角機動過程中,戰機先進入失速狀態,進一步會進入深失速區域內,戰機的空間位置、旋向及姿態角劇烈變化引發尾旋事故。戰機失速后會同時繞其三個體軸自轉,重心沿小半徑螺旋軌跡進行陡下降的自發運動[11]。這些運動由機翼造成。機翼是提供升力的主要部件,但戰機在失速后,左、右機翼氣流發生不對稱分離,兩機翼所產生的升力也就不對稱[11]，且兩機翼的升力損失程度也不相同,升力損失大的機翼就會發生機翼下沉,并繞縱軸滾轉。這種滾轉運動會使翼截面出現附加速度,使下沉半翼各截面的迎角增大,而上升半翼各截面的迎角減小,此時戰機的操縱性顯著變壞,甚至可能完全喪失。

在縱向大迎角機動過程中,從進入失速到改出,戰機能量損失非常大,損失率約為75.93%,此時俯仰角和迎角必須盡快恢復,這使戰機在大迎角機動階段能夠保持動態穩定,滿足過失速機動飛行要求。在進行大迎角機動飛行時,受氣流擾動,戰機處于非平穩狀態,使得戰機的穩定性極大降低,對于應對戰爭極為不利,這就要求戰機要有很好的增穩控制系統。

2大機動氣動力建模

具有推力矢量的戰機縱向運動非線性數學模型為:

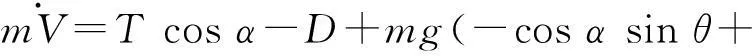
sinαcosθ)

cosαcosθ)

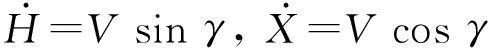
大迎角非定常氣動力的狀態空間數學模型為:

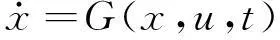
(1)

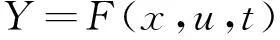
(2)

(3)

式中:m,n,p,q,r分別為狀態向量、輸入向量、向量函數、輸出向量和向量函數的維數。文獻[6]將上式用于描述戰機大迎角非定常氣動特性,輸入為迎角、俯仰角、偏航角等狀態參數及其時間的變化率,輸出為非定常氣動系數,即升力、阻力以及俯仰力矩系數等。對于流動分離的翼型和前緣分離破裂的三角翼,分別取翼型分離點和三角翼渦破裂位置作為內在狀態變量,建立了繞翼型和三角翼流動的大迎角非定常氣動力的狀態空間模型[12],并將此狀態空間模型的形式推廣到全機構型[13]:

(4)

(5)

(6)

(7)

3縱向大迎角機動仿真分析

如圖2所示,某型戰機大迎角機動全過程為:飛

行員迅速拉桿到底,戰機以350～500 km/h 的速度等高定直平飛，機頭上仰后迅速進入垂直向上位置,此時迎角達到 90°～100°,俯仰角最大可達到 100°～120°。由于大迎角機動過程中,戰機失速后速度很快在3～4 s 內減小到 110～122 km/h;本模型的氣動數據是戰機在迎角55°以下得到的,受氣動模型限制,本文數值仿真結果為迎角60°時所得，與Su-27縱向動態大迎角機動情況類似。

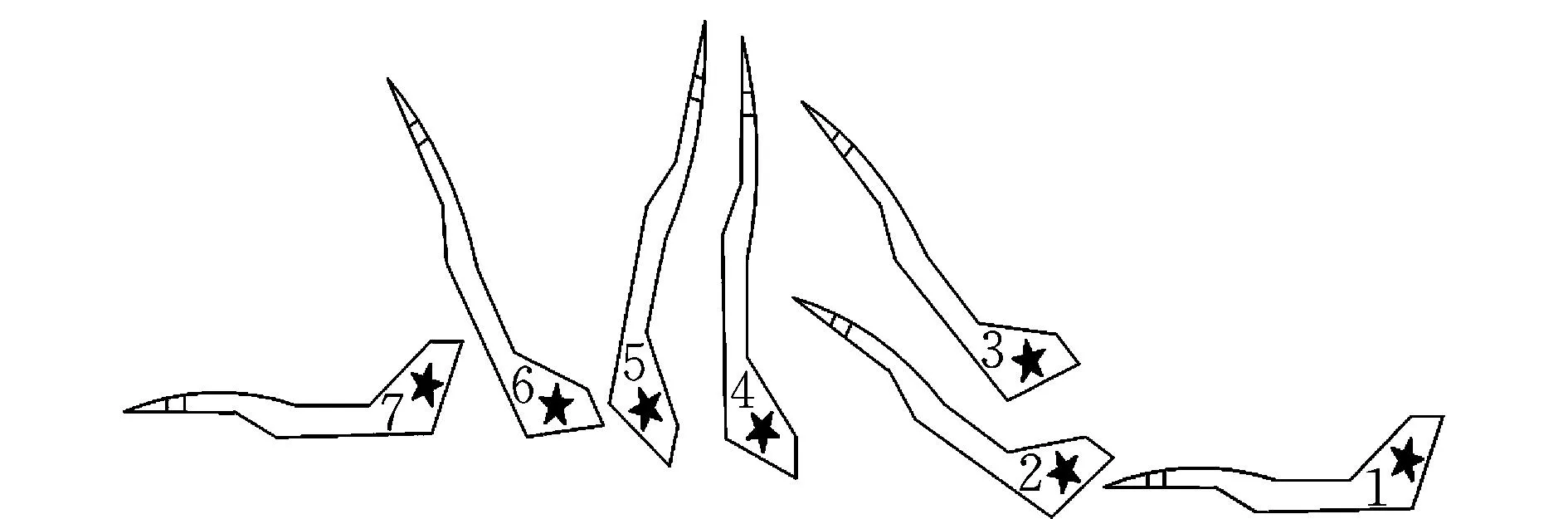
圖2　戰機縱向大迎角機動示意圖Fig.2　Diagram of aircraft longitudinal high AOA maneuver

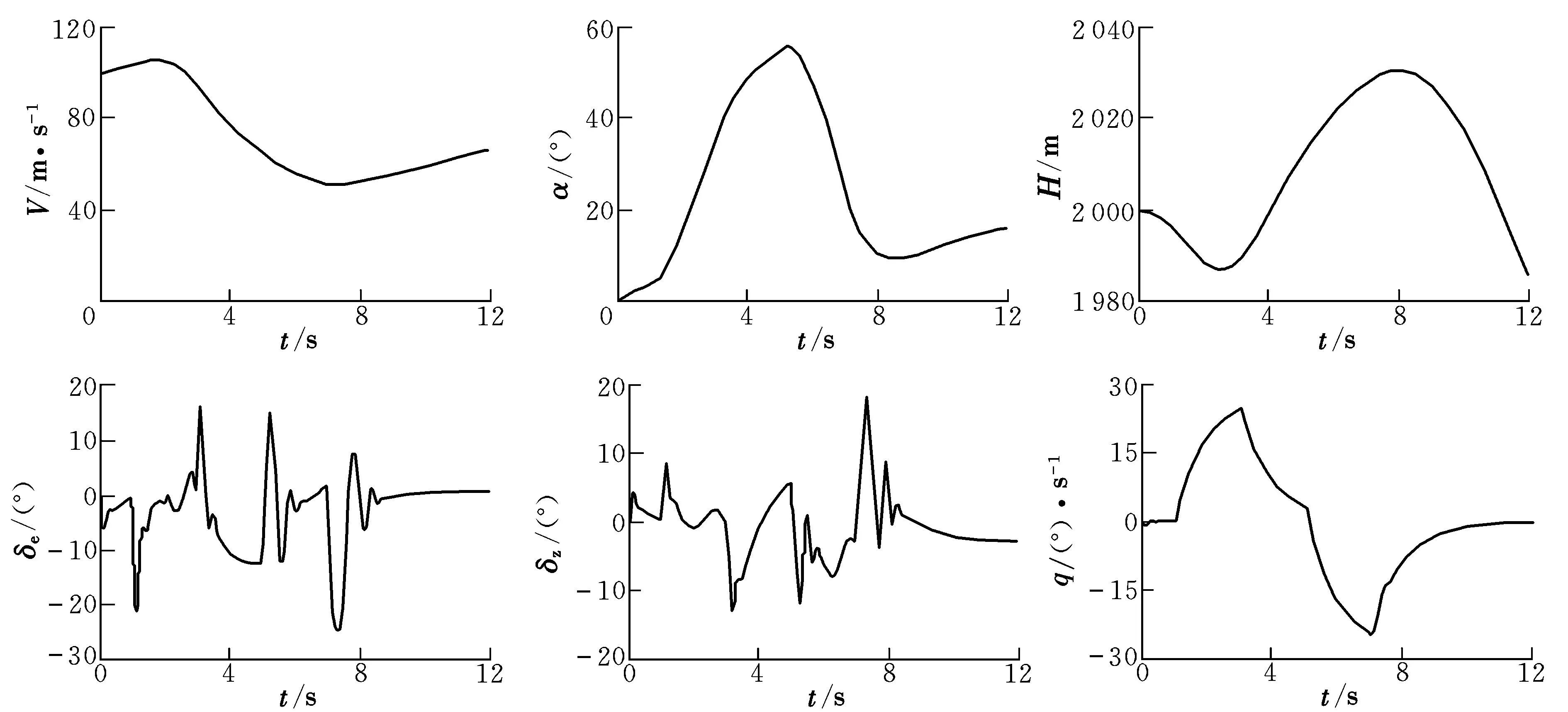
圖3　仿真曲線Fig.3　Simulation curves

由圖可知,戰機以100 m/s的速度進入機動,隨著迎角的增加,戰機高度增加,速度下降很快。到5.3 s時,戰機迎角達到55°,遠遠超過常規戰機機動中最大限制迎角30°[14]。隨著戰機的速度降到最小,約為49 m/s,高度增加到最大約2 030 m。此后操控戰機減小迎角,增大速度,減小高度,增加速度,約在8.3 s時,戰機迎角變化達到44°,速度恢復到53 m/s,隨后戰機逐漸增大速度,恢復到正常穩定飛行狀態,與實際機動基本接近。

在大迎角機動過程中,戰機平尾偏角、推力矢量舵偏角均未超過規定上限。速度逐漸增大時,戰機平尾偏角和推力矢量舵偏角緩慢增大,3 s時,推力矢量舵偏角達到最大,此時戰機的速度也達到最大,處于失速的臨界狀態。7 s后,戰機做大機動,平尾偏角和推力矢量舵偏角處于動態變化,最后逐漸趨于0°,說明戰機在機動過程中保持良好的動態穩定性。俯仰角速度在剛開始的1 s數值為0,隨著速度增大,3.2 s時達到最大,之后逐漸減小,7 s時達到最小,此時速度最小,戰機處于失速狀態,7 s之后,速度逐漸恢復到穩定飛行狀態,俯仰角速度也逐漸趨向于零。說明戰機在機動過程中能夠保持航向穩定。

仿真結果顯示,在大迎角縱向機動過程中,隨著俯仰角、迎角的增大,戰機的飛行速度降低,在到達最大迎角時,戰機速度從100 m/s降到了49 m/s,7 s后俯仰角速度恢復,速度也開始增加。可見,現代戰機在縱向大迎角機動過程中能量損失非常大,損失率約75.93%,此時迎角必須及時恢復到穩定飛行狀態的大小,因此現代戰機對發動機性能提出了更高要求,要求發動機具有較大的推重比,同時飛行控制系統的設計也同樣重要。

4結束語

現代戰機大迎角機動階段是一個獲得位置優勢、先敵瞄準、指向的過程。在近距空戰中,迎角的增大和速度方向推力矢量的減小,極易使戰機失速進而失穩。對于大迎角機動階段戰機失速問題,本文的研究結果表明:在大迎角機動過程中,戰機速度、平尾偏角、推力矢量舵偏角、俯仰角速度動態特性變化較大,能夠真實地反映實際機動狀態。由此得出,在近距離空戰大迎角機動時,戰機能夠保持動態穩定,滿足過失速機動飛行,為改善其飛行品質、提高作戰效能提供了理論依據。

參考文獻：

[1]張曙光,孫金標.最佳過失速機動研究[J].航空學報,2001,22 (4):289-292.

[2]張曙光,辛毅.基于過失速機動動力學的控制方法[J].飛行力學,2001,19(2):1-4.

[3]Greenwell D I.A review of unsteady aerodynamic modeling for flight dynamics of maneuverable aircraft[R].AIAA-2004-5276,2004.

[4]范本根.大迎角動態試驗及等離子體在前體流動控制中的應用[D].南京:南京航空航天大學,2010.

[5]孫海生,姜裕標,黃勇,等.現代戰斗機非定常空氣動力學及其風洞實驗研究[J].空氣動力學學報,2008,26(增刊):59-65.

[6]Goman M,Khrabrov A.State-space representation of aerodynamic characteristics of an aircraft at high angles of attack[J].Journal of Aircraft,1994,31(5):1109-1115.

[7]Wang Z,Lan C E,Brandon J M.Fuzzy logic modeling of nonlinear unsteady aerodynamics[R].AIAA-98-4351,

1998.

[8]姜久龍,李學仁,杜軍,等.飛機縱向非定常氣動力建模與辨識研究[J].空軍工程大學學報,2013,14(4):14-19.

[9]李林剛,高浩.戰機大迎角氣動數據的組成與應用[J].飛行力學,1997,15(1):1-7.

[10]汪清,何開鋒,錢煒祺,等.戰機大攻角空間機動氣動力建模研究[J].航空學報,2004,25(5):447-450.

[11]趙濤.大迎角失速/尾旋及反尾旋傘仿真計算研究[D]:西安:西北工業大學,2001.

[12]Fan Yigang,Lutze F H.Identification of an unsteady aerodynamic model at high angles of attack[R].AIAA-96-3407-CP,1996.

[13]楊立芝.大迎角氣動力數值模擬及建模研究[D].西安:西北工業大學,2004.

[14]黃智勇.超機動飛機的數學建模與運動仿真[D].西安:西安電子科技大學,2007.

(編輯：方春玲)

Research on the simulation of advanced fighter maneuvers at high AOA

ZHANG Jia-long1, YAO Hong2, JIANG Jiu-long1

(1.Aeronautics and Astronautics Engineering College,AFEU, Xi’an 710038, China;2.College of Science, AFEU, Xi’an 710051, China)

Abstract:By taking into consideration of the thrust vector and unsteady aerodynamic, aerodynamics and unsteady aerodynamic models are set up for the longitudinal maneuver of an advanced fighter. The numerical simulation is applied to analyze the speed, horizontal tail deflection, rudder deflection caused by thrust vector, pitching angle rate characteristics. The results show the parameters switching are consistent with real situation, and can effectively reflect the actual maneuvering conditions, thus providing the reference for the design of controllability and stability system.

Key words:high angle of attack; the simulation analysis; the unsteady aerodynamic; controllability and stability system

中圖分類號：V212.1

文獻標識碼：A

文章編號：1002-0853(2016)01-0010-04

作者簡介:張佳龍(1988-)，男，陜西楊凌人，碩士研究生，研究方向為先進控制理論。

基金項目:航空科學基金資助(20111396)

收稿日期:2015-07-29;

修訂日期:2015-10-15; 網絡出版時間:2015-10-26 09:33