基于Brown構(gòu)形場方法的二維收縮流模擬?

李路程,許曉陽

(1-西北工業(yè)大學(xué)應(yīng)用數(shù)學(xué)系，西安 710129;2-陜西理工學(xué)院數(shù)學(xué)與計(jì)算機(jī)科學(xué)學(xué)院，漢中 723001)

1 引言

采用Brown構(gòu)形場(Brownian configuration fields,BCF)方法[1,2]模擬粘彈性流體問題時，需要耦合求解宏觀尺度的守恒方程和介觀分子尺度的構(gòu)形方程.該方法繞開了采用本構(gòu)方程封閉求解流場控制方程的難點(diǎn)，因而可以摒棄本構(gòu)方程建立中潛在的不正確性.同時，該方法從介觀分子尺度求解聚合物分子構(gòu)形，故可以得到聚合物的分子信息.

守恒方程和構(gòu)形方程耦合求解的常見方法有有限元法(finite element method,FEM)[1,2]和有限體積法(finite volume method,FVM)[3-5].FEM能很好地適應(yīng)不規(guī)則區(qū)域，而在對流項(xiàng)的處理及對守恒方程的原始變量法求解方面實(shí)施起來比較繁瑣.雖然FVM的格式精度不高，但是它具有占用內(nèi)存少、穩(wěn)定性強(qiáng)和對流項(xiàng)處理簡單的優(yōu)勢；同時該方法求解的原守恒方程在每個控制體上都守恒，且物理意義明確.因此，將FVM與BCF方法相結(jié)合，是獲得聚合物分子信息的有效途徑.目前，基于BCF的有限體積方法(finite volume method based on Brownian configuration fields,FVMBCF)鮮有文獻(xiàn)研究.代向艷等[6,7]運(yùn)用FVMBCF方法模擬了Couette流和Poiseuille流，張僡鳳等[8]研究了FVMBCF方法的并行算法，并用之模擬了管道流.文獻(xiàn)[6–8]中流動問題的求解區(qū)域簡單，流動特性單一.因此，本文擬應(yīng)用FVMBCF方法模擬具有復(fù)雜流動特性的平板收縮流動問題，以考證該方法模擬復(fù)雜流動問題的可靠性.

2 守恒方程

對于不可壓縮的等溫粘彈性流動，在忽略體積力的情況下，無量綱形式的流場守恒方程[1]為連續(xù)方程

動量方程

其中u表示流體速度，Reynolds數(shù)Re表示流體慣性力與粘性力的比值，p表示壓力，τp表示聚合物應(yīng)力，粘度比β表示溶劑粘度與流體總粘度的比值.

粘彈性流動問題的流場控制方程包含守恒方程和封閉的應(yīng)力本構(gòu)方程.粘彈性流體本構(gòu)關(guān)系的復(fù)雜性和機(jī)理的不確定性，增加了本構(gòu)方程建立的難度，BCF方法恰恰繞開了這個難題.

3 BCF方法

BCF方法通過計(jì)算大量聚合物分子的構(gòu)形，根據(jù)其系綜平均得到聚合物應(yīng)力.再將介觀尺度獲得的應(yīng)力與宏觀尺度的守恒方程結(jié)合，從而求解粘彈性流場的控制方程.BCF方法求解得到的構(gòu)形在空間上光滑，確保計(jì)算所得的應(yīng)力光滑[3]；該方法還可以避免CONNFFESSIT(calculation of non-Newtonian fluid:finite element and stochastic simulation techniques)方法[9]中需要追蹤大量粒子軌道的問題.

3.1 分子模型

常用的聚合物分子模型有圖1所示的珠-簧(鏈)模型和珠-桿(鏈)模型.為了表征聚合物分子的粘彈特性，本文選用有限拉伸非線性彈性(finite extensible nonlinear elastic,FENE)珠-簧模型.

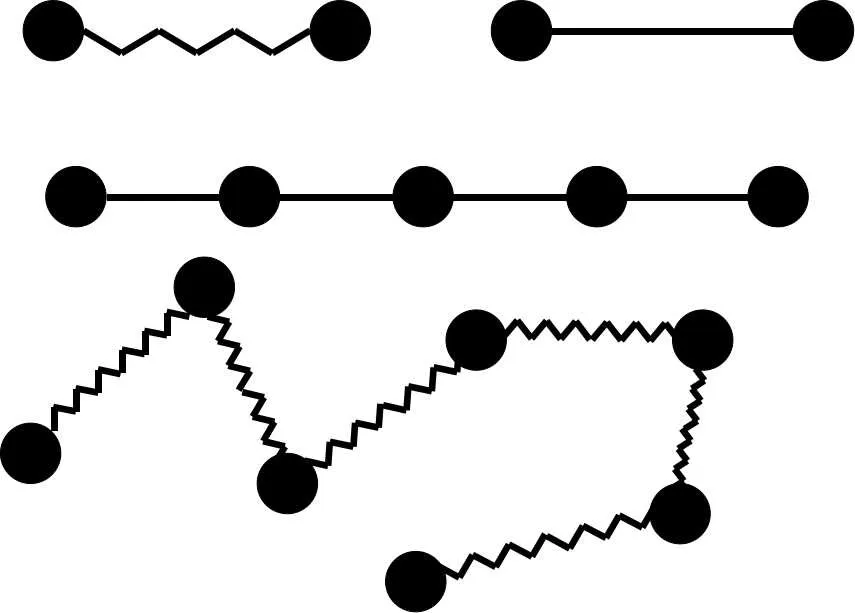
圖1:聚合物分子模型示意圖

FENE珠-簧模型的彈簧力[1]

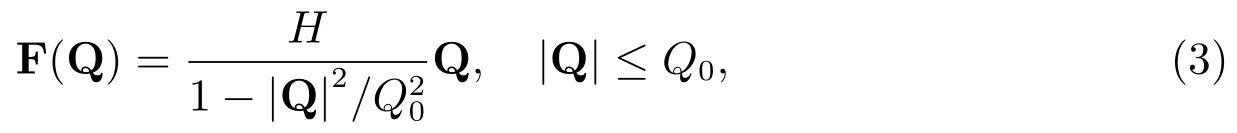
其中Q表示彈簧的構(gòu)形向量，|Q|是彈簧的長度，Q0是彈簧的最大拉伸量，H是彈簧的彈性系數(shù).

3.2 分子構(gòu)形演化方程

推導(dǎo)分子構(gòu)形演化方程，首先需要分析稀溶液中聚合物分子模型中珠子的受力情況.根據(jù)Newton第二定律，加速度為零時，珠子i所受的合力公式

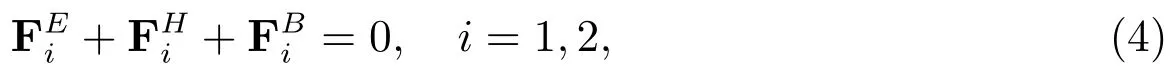
其中和分別代表珠子i所受的彈力、粘滯力和Brown隨機(jī)力.

彈力

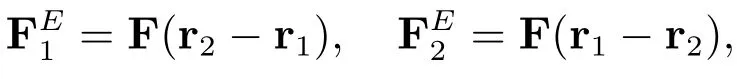
由式(3)給出；粘滯力Brown隨機(jī)力

計(jì)算中常近似為

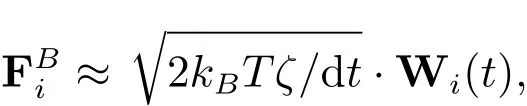
其中ri表示珠子i的位置向量，是i號珠子的速度，表示珠子i處溶劑的速度，ζ為小球與溶劑的摩擦系數(shù)，kB為Boltzmann常數(shù)，T表示絕對溫度，δ表示單位張量，是Markov過程，服從分布

整理方程(4)，得到

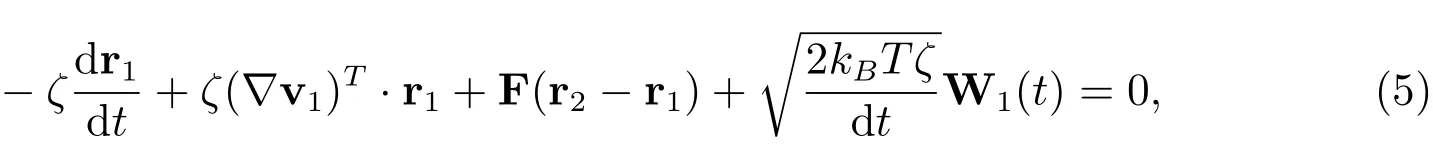
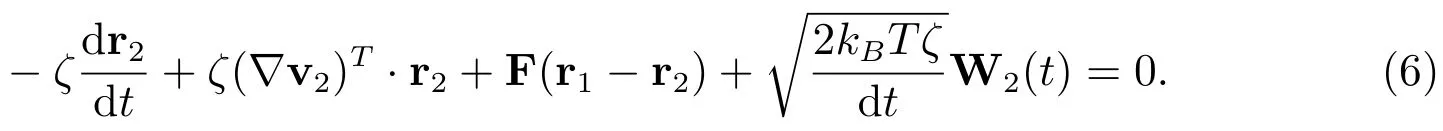
上面兩式相減，令Q=r2?r1，根據(jù)隨體導(dǎo)數(shù)公式得到

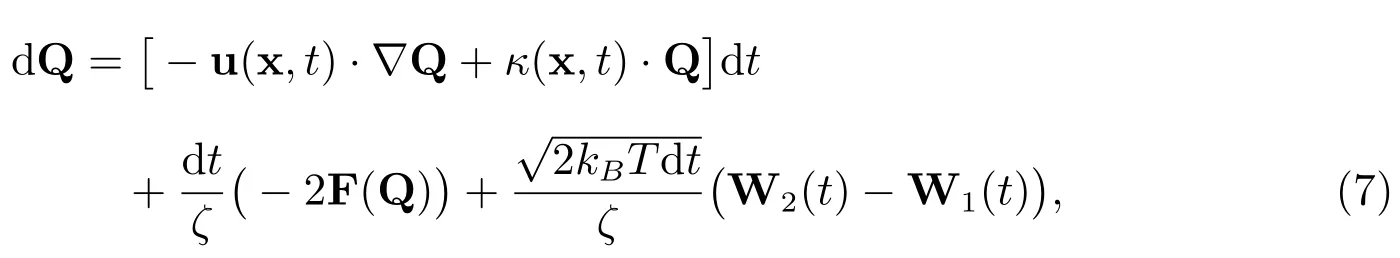
(7)式兩端同時除以又有得到

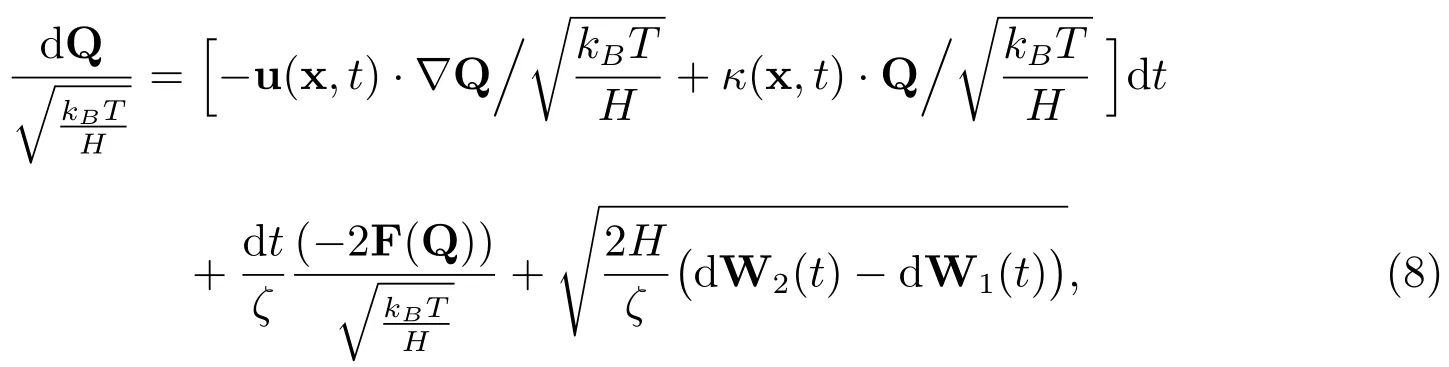
對(8)式進(jìn)行無量綱處理，得到

其中Weissenberg數(shù)，L為流場的特征長度，U為流場的特征速度，Q表示分子模型彈簧的構(gòu)形向量，κ表示速度梯度的轉(zhuǎn)置，F(xiàn)表示分子模型中彈簧的彈力.

求解方程(9)得到分子構(gòu)形向量Q后，則由Kramers表達(dá)式[3]計(jì)算聚合物應(yīng)力

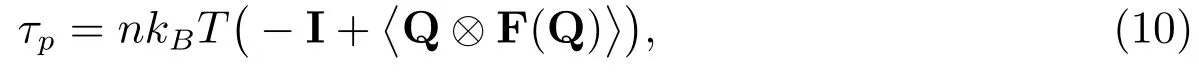
其中nkBT為求解參數(shù)，I表示二階單位矩陣，〈Λ〉表示構(gòu)形空間上的系綜平均，運(yùn)算符?表示兩個向量的外積，其表達(dá)式為

3.3 施加方差縮減技術(shù)的BCF方法

1)設(shè)置構(gòu)形場：在任一計(jì)算節(jié)點(diǎn)處，設(shè)置Nf個編號為j(j=1,K,Nf)的珠-簧模型；在所有節(jié)點(diǎn)處編號為j(j=1,K,Nf)的珠-簧模型都具有相同的初始構(gòu)形，并經(jīng)歷相同的隨機(jī)過程；

2)引入構(gòu)形控制變量：初始時刻流體處于靜止?fàn)顟B(tài)，分子構(gòu)形服從Gauss隨機(jī)分布N(0,1)；流動過程中，分子構(gòu)形的演化由方程(9)來描述；流動趨于穩(wěn)定時，分子構(gòu)形最終服從均勻隨機(jī)分布U(0,1).這表明當(dāng)前狀態(tài)應(yīng)力的變化與平衡狀態(tài)應(yīng)力的變化相關(guān)，因此，可以選取初始狀態(tài)服從均勻隨機(jī)分布，且流動過程中與Q經(jīng)歷相同隨機(jī)過程的構(gòu)形作為Q的控制變量[9].針對FENE模型，滿足方程

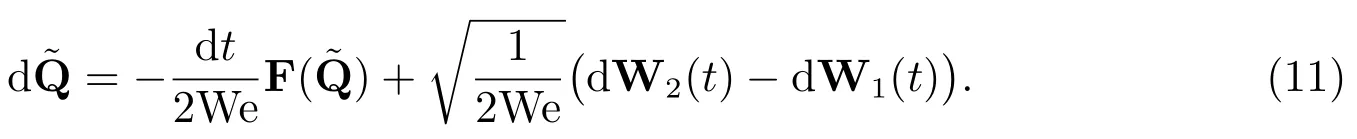
根據(jù)式(10)及其恒等變形，有

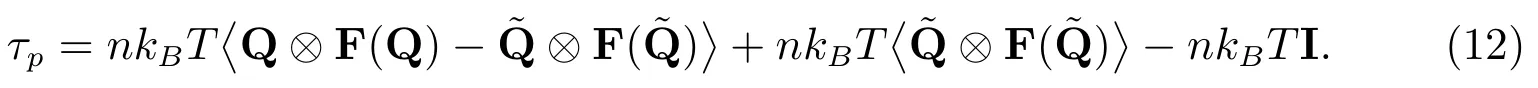
設(shè)根據(jù)式(12)和外積定義，應(yīng)力各分量為

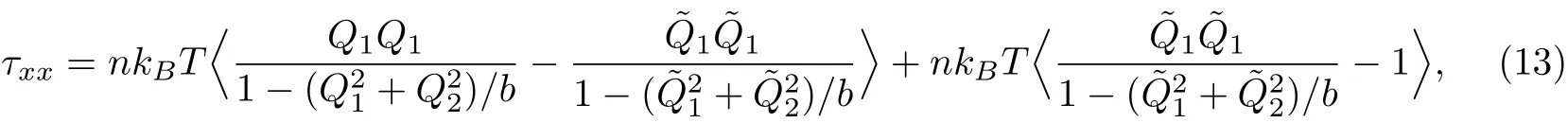
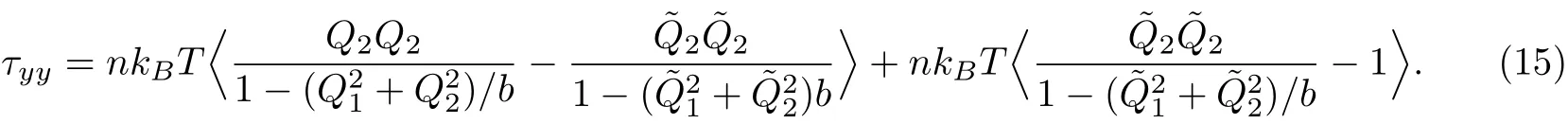
至此，給出了施加方差縮減技術(shù)的BCF方法計(jì)算聚合物應(yīng)力各分量的表達(dá)式.根據(jù)統(tǒng)計(jì)學(xué)知識，控制變量的引入，不會改變統(tǒng)計(jì)量

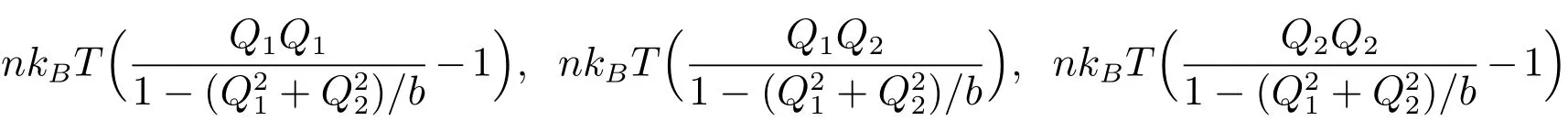
的數(shù)學(xué)期望；同時，由于控制變量法的統(tǒng)計(jì)學(xué)性質(zhì)，它們?nèi)齻€統(tǒng)計(jì)量的隨機(jī)誤差將大大地降低.因此，控制變量法的統(tǒng)計(jì)學(xué)性質(zhì)使得構(gòu)形控制變量的引入，能夠有效地減少應(yīng)力的隨機(jī)誤差.

4 數(shù)值計(jì)算方法

基于Brown構(gòu)形場方法求解粘彈性流動問題時，首先通過求解聚合物分子的構(gòu)形方程(9)和控制變量方程(11)，再由式(13)計(jì)算聚合物應(yīng)力，然后將介觀尺度求解的應(yīng)力與宏觀尺度的守恒方程(1),(2)結(jié)合，從而得到描述粘彈性流動問題的宏觀物理量.

4.1 同位網(wǎng)格FVM

本文采用同位網(wǎng)格FVM[5]離散守恒方程(1),(2)，其中對流項(xiàng)的離散采用一階迎風(fēng)格式，該格式簡單且易于實(shí)施.計(jì)算中，所有變量置于圖2所示的同一套網(wǎng)格.圖2中實(shí)線交點(diǎn)為計(jì)算物理量的存儲點(diǎn)，虛線為控制體界面，節(jié)點(diǎn)位于控制體的中心.

我撕到最后一頁時，聽到有人在樓下跟我媽講話，聽我媽那反應(yīng)就知道來人不是扒鍋街的人，她平時的嗓門震得門框都會抖三抖，哪像那會，明明想笑卻拼命壓著喉嚨，像只有痰的老母雞。

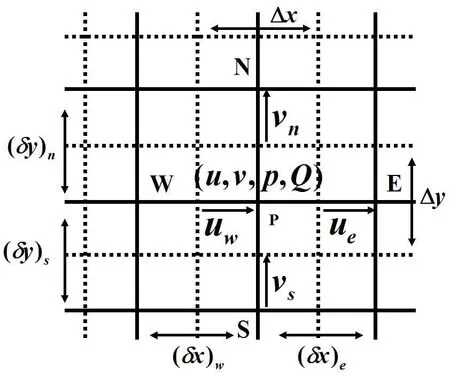
圖2:同位網(wǎng)格示意圖

將連續(xù)方程(1)在圖2所示的P控制體上進(jìn)行積分，其離散格式

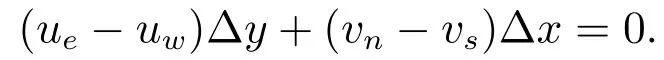
二維動量守恒方程(2)的通量表達(dá)形式

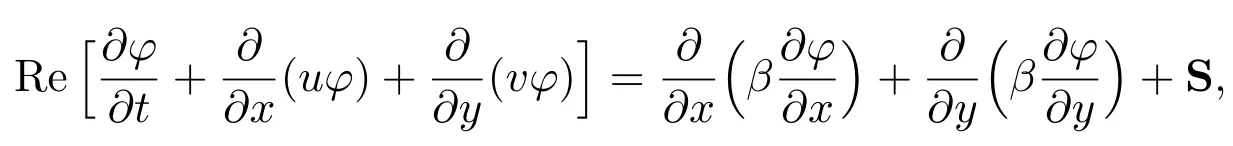
其中

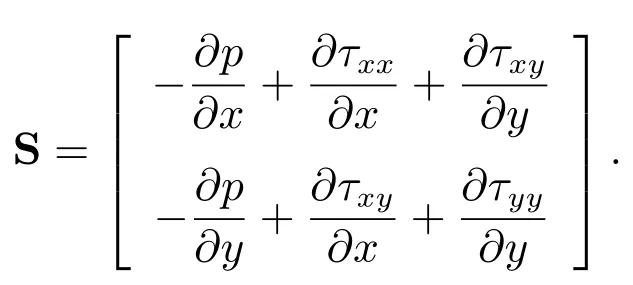
時間項(xiàng)的離散格式精度為一階；用控制容積積分法對對流-擴(kuò)散項(xiàng)進(jìn)行離散

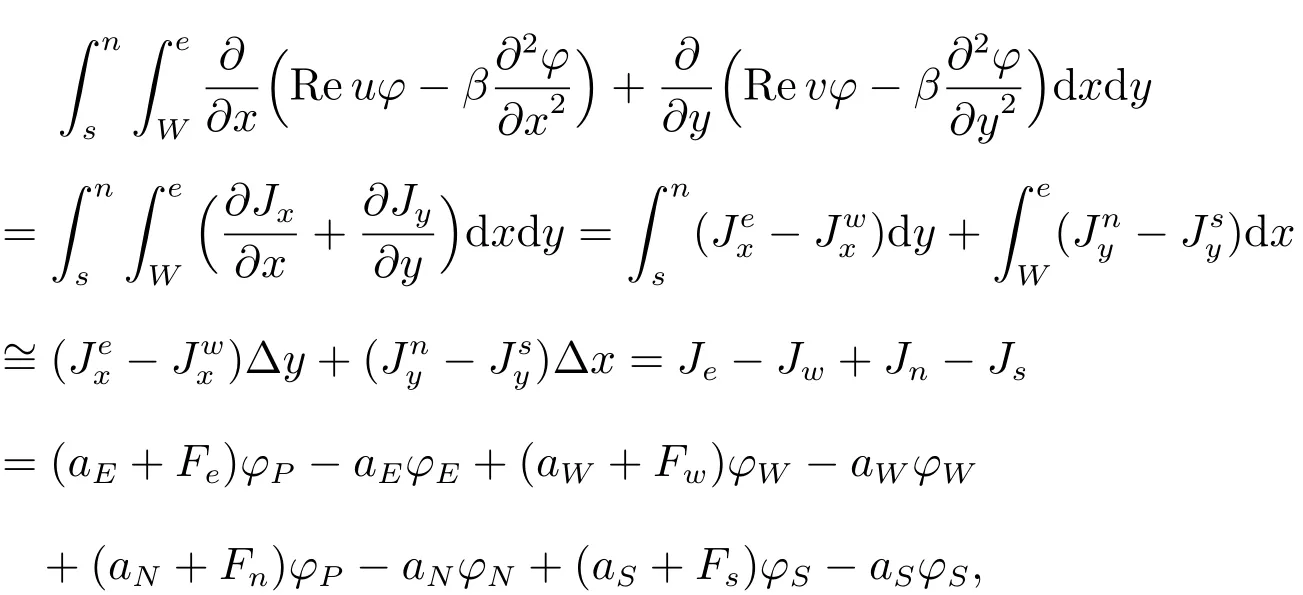
精度為一階；其中

源項(xiàng)中應(yīng)力采用顯式差分格式離散，壓力采用線性插值計(jì)算，精度均為一階；從而有限體積法部分的整體格式精度為一階.BCF方法是隨機(jī)方法，難以進(jìn)行精度分析.設(shè)維數(shù)d，流動時間步FLAG，收斂判定條件數(shù)flag，構(gòu)形數(shù)目Nf，計(jì)算點(diǎn)個數(shù)M，本文算法的計(jì)算量約為

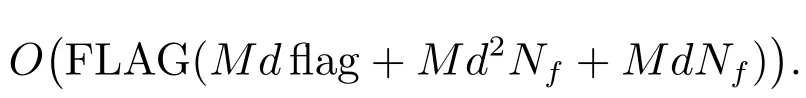
4.2 FVMBCF方法的算法流程

基于并行程序的FVMBCF方法模擬粘彈性流動的具體算法流程如下：

步驟1準(zhǔn)備階段設(shè)用P個處理機(jī)進(jìn)行計(jì)算，在根進(jìn)程上給定初始的速度u0，在每個進(jìn)程上給定初始的分子構(gòu)形和構(gòu)形控制變量，初始構(gòu)形和構(gòu)形控制變量在空間上分別服從Gauss隨機(jī)分布和均勻隨機(jī)分布，它們的數(shù)值可由相應(yīng)的分布函數(shù)N(0,1)和U(0,1)獨(dú)立取樣得到；

步驟2計(jì)算速度和壓力將初始或上一時間步的聚合物應(yīng)力代入方程(1)和(2)，并用FVM求解，即可得到新的速度和壓力；

步驟3計(jì)算構(gòu)形和構(gòu)形控制變量用新的速度u計(jì)算速度梯度κ，并將速度梯度κ廣播到每一個進(jìn)程中去.當(dāng)已知速度梯度κ及上一時間步的分子構(gòu)形和構(gòu)形控制變量時，根據(jù)方程(9)和(11)，可計(jì)算得到當(dāng)前時間步的分子構(gòu)形和構(gòu)形控制變量

步驟4計(jì)算聚合物應(yīng)力在每個進(jìn)程上，將步驟3中計(jì)算得到的當(dāng)前時間步的分子構(gòu)形和構(gòu)形控制變量代入式(13)，并歸約到0進(jìn)程上求和，計(jì)算聚合物應(yīng)力

步驟5若收斂條件滿足，計(jì)算結(jié)束；否則返回步驟2.

5 數(shù)值算例

5.1 Couette流

為了驗(yàn)證施加方差縮減技術(shù)的FVMBCF方法的有效性，本文首先基于FENE珠-簧模型，模擬聚合物稀溶液的平板Couette流.

在該流動問題中，聚合物流體被限制在兩個距離為L=1.0的平行平板間.當(dāng)t＜0時，流體和兩個平板靜止；當(dāng)t=0，下平板開始以恒定的水平速度u=1.0沿x軸正方向移動，壁面邊界滿足無滑移邊界條件，初始狀態(tài)為平衡態(tài).為了與文獻(xiàn)中的結(jié)果進(jìn)行對比，本文采用文獻(xiàn)[11]中的模型參數(shù)，即

圖3(a)刻畫了不同時刻、不同y值處的速度.圖3(b)描述了四個不同位置y=0.2,y=0.4,y=0.6,y=0.8處的速度演化.由圖3(b)可知，越靠近下平板的位置，速度過沖現(xiàn)象發(fā)生的越早.圖3(c)描述了圖3(b)中的四個位置處的應(yīng)力演化，應(yīng)力曲線光滑.模擬結(jié)果與文獻(xiàn)[11]的結(jié)果吻合，從而驗(yàn)證了施加方差縮減技術(shù)的FVMBCF方法的有效性.

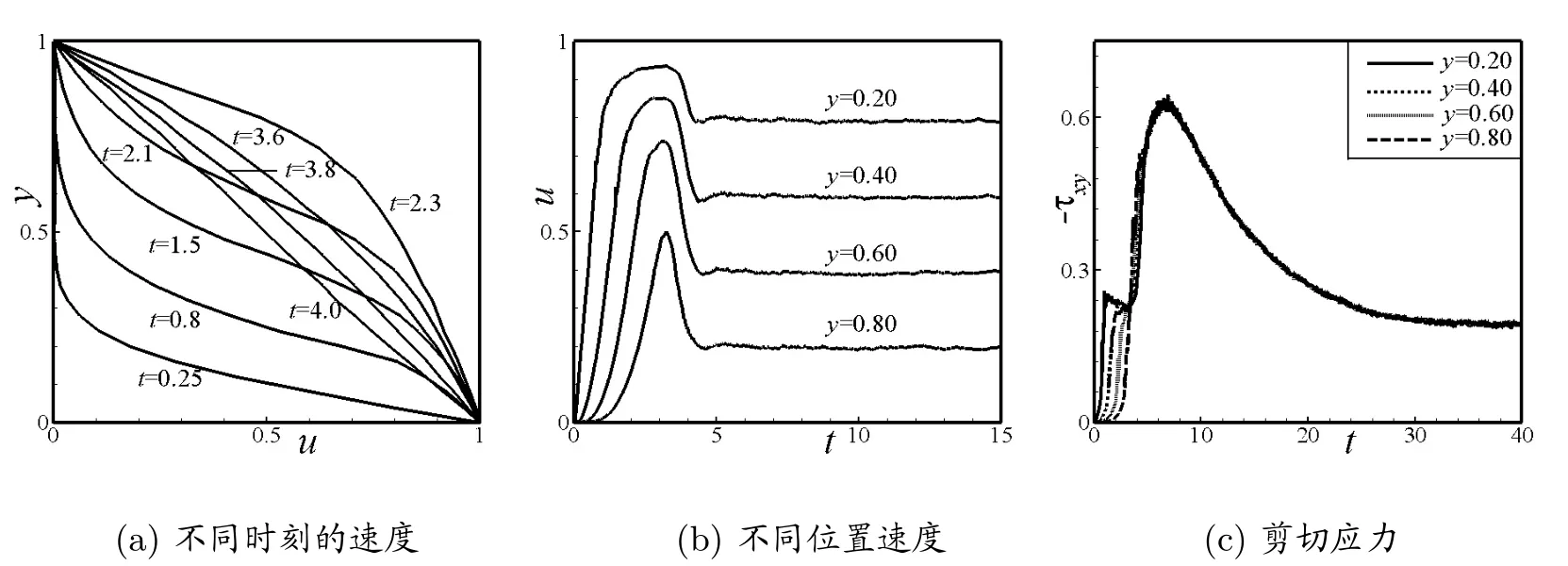
圖3:平板Couette流速度和應(yīng)力分布

5.2 平板收縮流

4:1平板收縮流能夠反映流體經(jīng)旋轉(zhuǎn)、剪切和拉伸變形后的流動特性.收縮口附近存在的應(yīng)力奇點(diǎn)，使流動問題的數(shù)值解在收縮口附近存在大梯度變化.因此，對4:1粘彈性收縮流動問題的模擬，更能檢驗(yàn)本文數(shù)值方法的有效性.

同時，由于應(yīng)力奇點(diǎn)的存在及FVMBCF方法在計(jì)算過程中不可避免地產(chǎn)生隨機(jī)誤差，導(dǎo)致在收縮口附近應(yīng)力出現(xiàn)振蕩.所以本節(jié)先給出施加方差縮減技術(shù)的FVMBCF方法的數(shù)值模擬結(jié)果，然后在5.3節(jié)給出關(guān)于施加方差縮減技術(shù)必要性的討論.

由于收縮流的對稱特性，僅選取圖4所示y≥0的計(jì)算區(qū)域.將計(jì)算區(qū)域劃分成四個部分，采用疏密不同的拼接網(wǎng)格.四個區(qū)域的網(wǎng)格分別取為：42×12、42×77、32×12和22×12.計(jì)算中固壁面邊界滿足無滑移邊界條件.無量綱參數(shù)選取

收斂判定條件閾值5×10?5.入口速度為

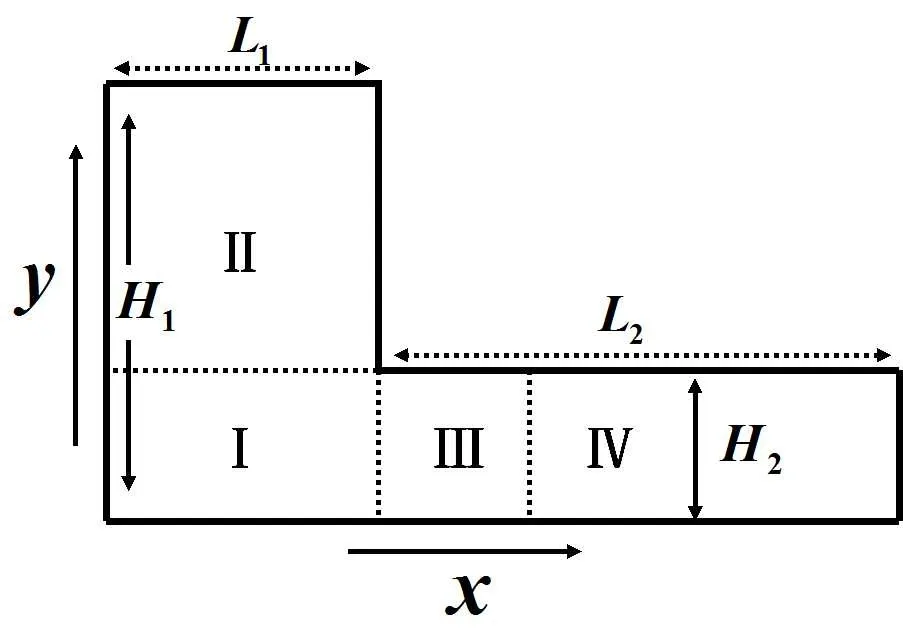
圖4:收縮流動示意圖

圖5給出了不同We下收縮口附近的流線分布.由圖5可知，在收縮口上游和下游處流動充分發(fā)展；在收縮口附近形成強(qiáng)拉伸區(qū)域；在上游拐角處，流動以旋轉(zhuǎn)為主，形成角渦，且隨著We的增大，渦流區(qū)的范圍減小，渦心位置上升，角渦變小.

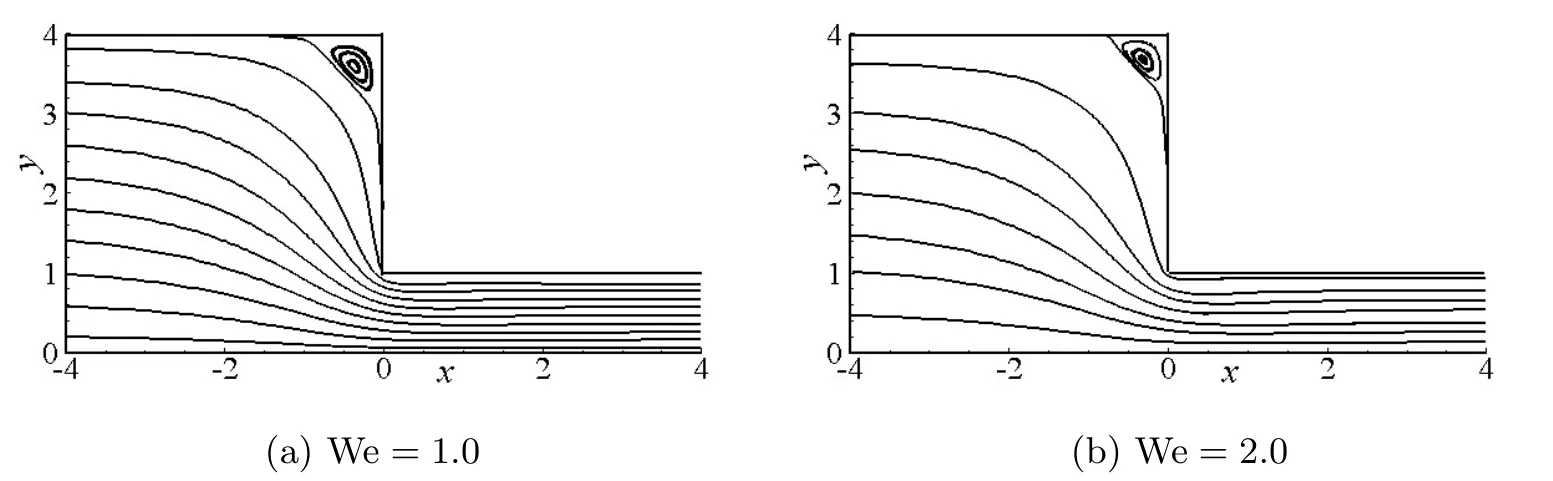
圖5:不同We下收縮口附近的的流線分布

圖6給出了We=1時收縮口附近的應(yīng)力等值線分布.由圖6可以看出，在收縮口附近，應(yīng)力等值線光滑且分布密集，說明在收縮口處應(yīng)力變化劇烈.圖5與圖6的數(shù)值結(jié)果與文獻(xiàn)[12,13]相一致.

圖6:We=1.0時收縮口附近的應(yīng)力等值線分布

圖7描述了流動穩(wěn)定時收縮口附近y=1水平層面的速度、剪切應(yīng)力及第一法向應(yīng)力差的分布情況.由圖7可知，隨著We的增大，速度過沖現(xiàn)象更加明顯.另外，剪切應(yīng)力和第一法向應(yīng)力差過沖現(xiàn)象加劇，收縮口附近的應(yīng)力梯度很大，各應(yīng)力分量均在收縮口附近取得最大值，且峰值隨著We的增大而增加.這說明在收縮口附近，剪切拉伸作用隨We的增大而加強(qiáng).

圖7:收縮口附近y=1的速度u、剪切應(yīng)力τxy、第一法向應(yīng)力差分布

5.3 方差縮減技術(shù)

圖8描述了未施加及施加方差縮減技術(shù)情形下收縮口附近應(yīng)力等值線的分布情況(左列是未施加方差縮減技術(shù)的結(jié)果，右列是施加方差縮減技術(shù)的結(jié)果).由圖8可知，未施加方差縮減技術(shù)時，收縮口附近的應(yīng)力等值線出現(xiàn)振蕩現(xiàn)象；而施加方差縮減技術(shù)后，振蕩現(xiàn)象消失，應(yīng)力各分量等值線均變得光滑.這說明方差縮減技術(shù)能夠很好地抑制收縮口附近的應(yīng)力振蕩.

圖9給出了y=0.52位置處應(yīng)力的數(shù)值結(jié)果，圖中小方框內(nèi)曲線是對收縮口附近(圖中圓形區(qū)域)應(yīng)力分布情形的放大處理.由圖9可知施加方差縮減技術(shù)后應(yīng)力的數(shù)值曲線較未施加的應(yīng)力數(shù)值曲線光滑，振蕩現(xiàn)象消失；但應(yīng)力各分量的數(shù)值減小.這說明了FVMBCF方法施加方差縮減技術(shù)時具有能夠確保獲得光滑應(yīng)力解的優(yōu)點(diǎn)，但是同時存在著消弱應(yīng)力解數(shù)值精度的缺陷.

圖8:未施加及施加方差縮減技術(shù)情形下收縮口附近應(yīng)力等值線的分布情況

圖9:y=0.52位置處應(yīng)力的數(shù)值結(jié)果

施加方差縮減技術(shù)時，由于控制變量參與計(jì)算，使得構(gòu)形向量的總計(jì)算量將近增加一倍.但是模擬結(jié)果顯示：同樣基于四個并行進(jìn)程，在選取相同收斂閾值的條件下，施加方差縮減技術(shù)的數(shù)值模擬耗時(57285.5s)比未施加方差縮減技術(shù)的數(shù)值耗時(56237.4s)僅多1.8%.這表明方差縮減技術(shù)能夠在計(jì)算時間微量增加的條件下，很好地抑制應(yīng)力的振蕩現(xiàn)象，其穩(wěn)定性能良好.

6 結(jié)束語

本文給出了施加方差縮減技術(shù)的FVMBCF方法及其求解流程，模擬了Couette流和4:1收縮流的粘彈性流動問題.數(shù)值結(jié)果表明：

1)該方法可以準(zhǔn)確地模擬包含應(yīng)力奇異點(diǎn)的復(fù)雜流動問題，計(jì)算結(jié)果可靠，算法易于實(shí)現(xiàn)；

2)該方法具有穩(wěn)定性強(qiáng)和對流項(xiàng)處理簡單的優(yōu)點(diǎn)，且應(yīng)力數(shù)值解具有光滑特性；

3)方差縮減技術(shù)能夠很好地抑制收縮口附近的應(yīng)力振蕩現(xiàn)象.

參考文獻(xiàn)：

[1]Abedijaberi A,Khomami B.Sedimentation of a sphere in a viscoelastic fluid:a multiscale simulation approach[J].Journal of Fluid Mechanics,2012,694(1):78-99

[2]Abedijaberi A,Khomami B.Continuum and multi-scale simulation of mixed kinematics polymeric flows with stagnation points:closure approximation and the high Weissenberg number problem[J].Journal of Non-Newtonian Fluid Mechanics,2011,166(11):533-545

[3]Owens R G,Phillips T N.Computational Rheology[M].London:Imperial College Press,2002

[4]陶文銓.數(shù)值傳熱學(xué)(第2版)[M].西安：西安交通大學(xué)出版社，2001 Tao W Q.Numerical Heat Transfer(2nd Edition)[M].Xi’an:Xi’an Jiaotong University Press,2001

[5]宋道云.同位網(wǎng)格有限體積法及其在粘彈性液體收縮流數(shù)值模擬中的應(yīng)用研究[D].上海：華東理工大學(xué)，2002 Song D Y.The algorithm of collocated-grid finite volume method and its application of numerical simulation in a contraction flow for viscoelastic fluids[D].Shanghai:East China University of Science and Technology,2002

[6]代向艷，歐陽潔，張小華，等.基于Brown構(gòu)形場的有限體積法在聚合物流動模擬中的應(yīng)用[J].工程數(shù)學(xué)學(xué)報，2011,28(5):642-654 Dai X Y,Ouyang J,Zhang X H,et al.Simulation of the polymeric flows using finite volume method based on Brownian con figuration fields[J].Chinese Journal of Engineering Mathematics,2011,28(5):642-654

[7]代向艷，歐陽潔.平板Couette流場中聚合物流變性質(zhì)及分子構(gòu)象的數(shù)值模擬[J].高分子材料科學(xué)與工程，2011,27(3):157-161 Dai X Y,Ouyang J.Rheological properties and molecular con figuration of polymer solution in planar Couette flow[J].Polymer Materials Science and Engineering,2011,27(3):157-161

[8]張僡鳳，歐陽潔，代向艷.耦合有限體積法的Brown構(gòu)型場并行算法研究[J].計(jì)算物理學(xué)報，2012,29(1):17-24 Zhang H F,Ouyang J,Dai X Y.Paralle algorithm for Brownian con figuration fields with finite volume method[J].Chinese Journal of Computational Physics,2012,29(1):17-24

[9]Bonvin J,Picasso M.Variance reduction methods for CONNFFESSIT-like simulations[J].Journal of Non-Newtonian Fluid Mechanics,1999,84(2-3):191-215

[10]ttinger H C,van den Brule B,Hulsen M A.Brownian con figuration fields and variance reduced CONNFFESSIT[J].Journal of Non-Newtonian Fluid Mechanics,1997,70(3):255-261

[11]Tran-Canh D,Tran-Cong T.Element-free simulation of dilute polymeric flows using Brownian con figuration fields[J].Korea-Australia Rheology Journal,2004,16(1):1-15

[12]Aboubacar M,Webster M F.A cell-vertex finite volume/element method on triangles for abrupt contraction viscoelastic flows[J].Journal of Non-Newtonian Fluid Mechanics,2001,98(2-3):83-106

[13]Edussuriya S S,Williams A J,Bailey C.A cell-centred finite volume method for modelling viscoelastic flow[J].Journal of Non-Newtonian Fluid Mechanics,2004,117(1):47-61