一類具有非線性發生率的SEIR傳染病模型的全局穩定性分析?

宋修朝李建全楊亞莉

(1-空軍工程大學理學院，西安 710051;2-陜西師范大學數學與信息科學學院，西安 710062)

1 引言

由Kermack和Mckendrick在1927年提出的倉室模型[1]是迄今為止研究傳染病動力學的最基本的模型.目前，大多數模型仍假設發生率為雙線性型的或標準型的[1-3].鑒于很多傳染病的傳播機制并沒有完全為人所知，所以近年來具有非線性發生率的傳染病模型越來越受到重視[4-10]，其中文獻[4–7]考慮了非線性發生率為(q和p是正數)的傳染病模型，文獻[8–10]考慮了非線性發生率為g(I)S的傳染病模型.Korobeinikov和Maini[11]研究了非線性發生率為f(S,I,N)的傳染病模型，函數f(S,I,N)滿足如下條件：

1)

2)對于所有的S,I＞0;

3)對所有的S,I＞0.

該文在一定條件下，證明了模型的全局穩定性.

文獻[9]考慮了非線性發生率為g(I)S的時滯的SEIR傳染病模型，其中β表示一個染病者的傳染能力，1/(1+εI)表示當染病者I數目增加時其對發生率的影響.文獻[10]考慮了非線性發生率也為g(I)S的SIRS傳染病模型，其中(H是正數).顯然，g(I)都滿足

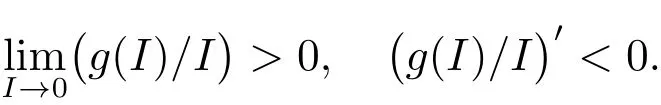
所以，我們將考慮一類具有形式為f(S)g(I)的非線性發生率的SEIR傳染病模型，其中函數f(S)和g(I)滿足如下條件：

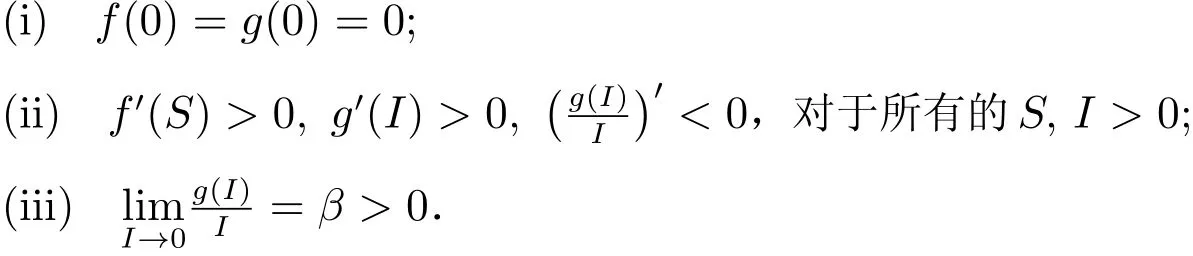
本文考慮的模型是對文獻[9]中所考慮模型的發生率的推廣，也是對文獻[10]中所考慮模型的推廣，并且得到了模型全局穩定性的充要條件.在文獻[12]中，作者提出了證明具有雙線性發生率的傳染病模型的全局穩定性的一種代數方法.我們將利用此代數方法證明本文的主要結論.

2 模型及平衡點的存在性

考慮如下傳染病模型

在模型(1)中，總人口分為四個倉室：易感者S(t)、潛伏者E(t)、傳染者I(t)和恢復者R(t).μA是總人口的常數輸入；μ是自然死亡率；q是潛伏者向傳染者的轉換率；γ是傳染者的恢復率；α是因病死亡率.函數f(S)和g(I)滿足條件(i),(ii)和(iii).

模型(1)中前三個方程與R無關，因此，考慮如下子系統

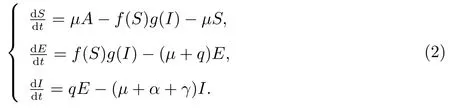
由于

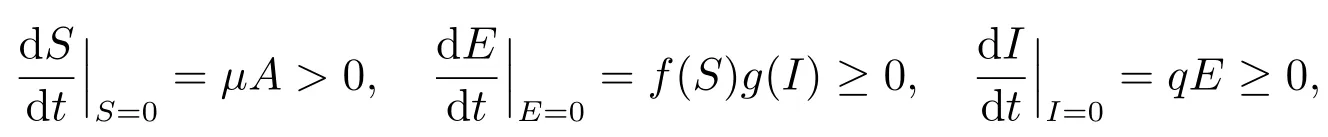
所以系統(2)的初值在R3+中的解的非負性得到了保證.將系統(2)的三個方程相加可得

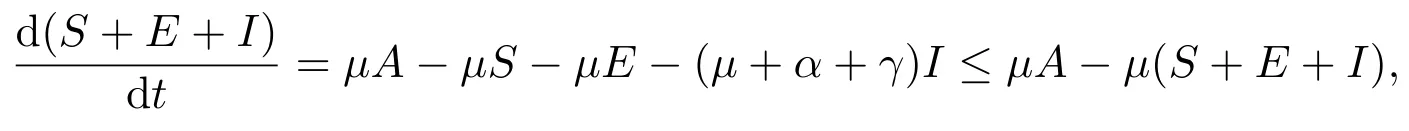
則

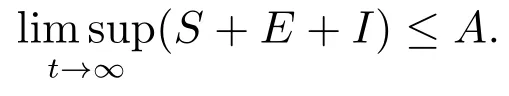
因此，集合是系統(2)的一個正不變集.

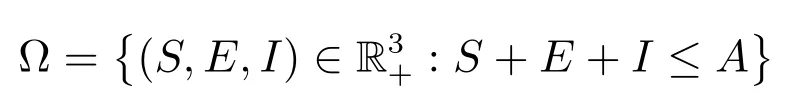
顯然系統(2)總存在一個無病平衡點P0(A,0,0).利用再生矩陣[13]可求得系統(2)的基本再生數

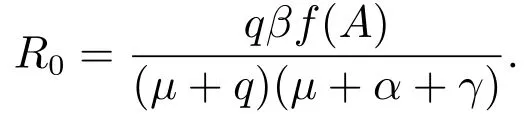
系統(2)的地方病平衡點由方程組

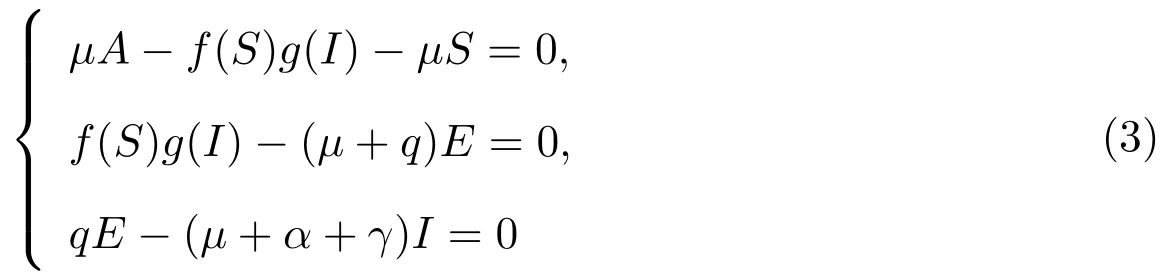
確定.由(3)的最后一個方程可得

將(3)的前兩個方程相加得

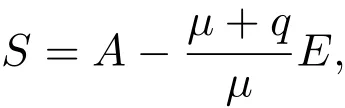
所以

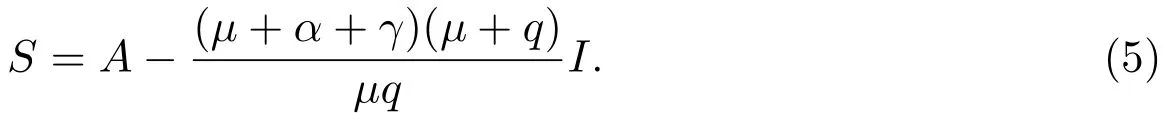
為了保證S＞0，只需

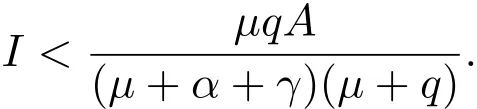
當I/=0時，由(3)的第二個方程和(4)可知

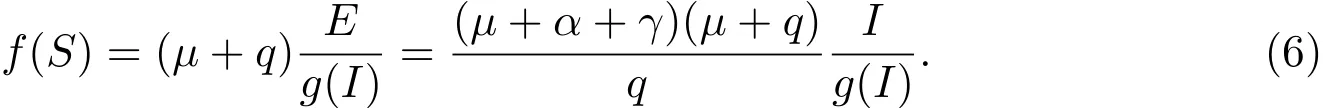
將(5)代入(6)，得

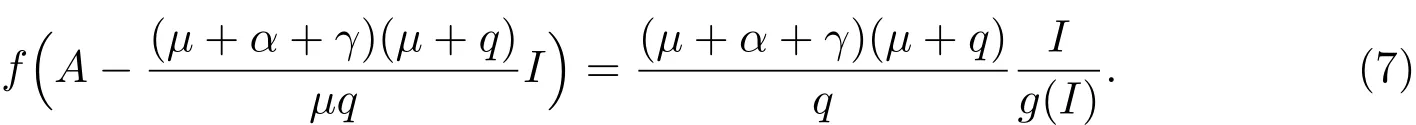
令

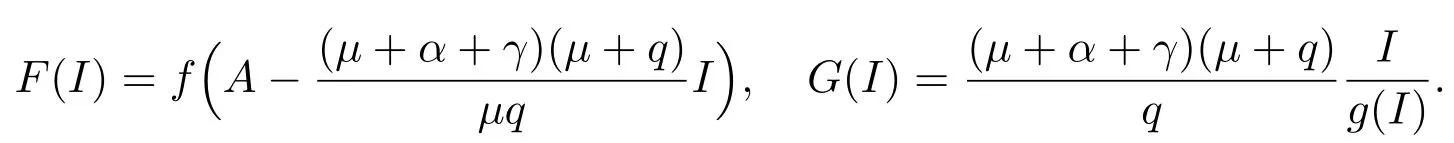
因為f′(S)＞0，所以當

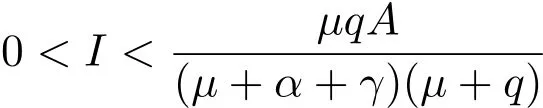
時，函數F(I)是遞減的，并且

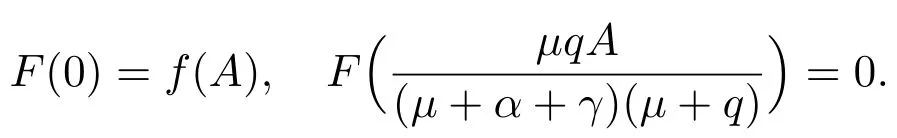
由條件(ii)和(iii)可知：函數G(I)是遞增的，并且

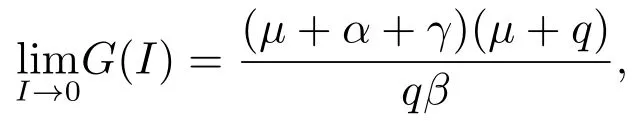
所以當R0＞1，即

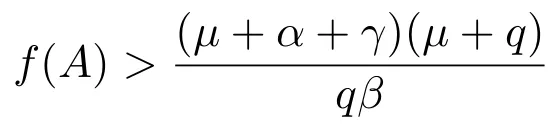
時，方程(7)存在唯一的正根I?，且

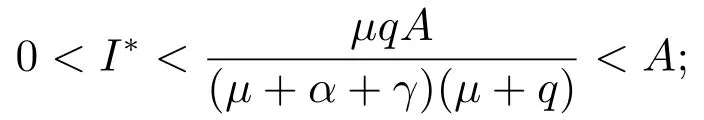
當R0≤1時，方程(7)不存在正根.此時，系統(2)不存在地方病平衡點.所以我們有如下結論：

定理1系統(2)總存在一個無病平衡點當除了外，系統(2)還存在唯一的一個地方病平衡點其中

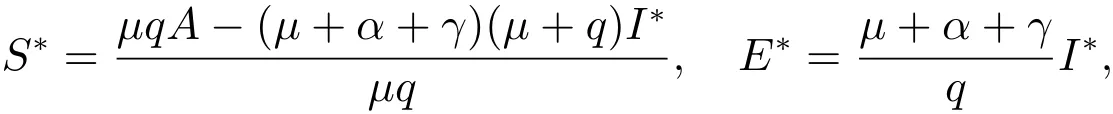
I?是方程(7)在區間內的正根.

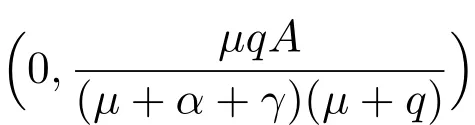
3 平衡點的全局穩定性

在本節中，我們將證明系統(2)的平衡點的全局穩定性.第一個結論是：

定理2當R0≤1時，系統(2)的無病平衡點P0(A,0,0)是全局穩定的；當R0＞1時，P0是不穩定的.

證明 構造如下Lyapunov函數

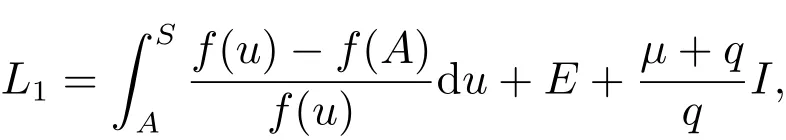
計算L1沿系統(2)解的全導數得

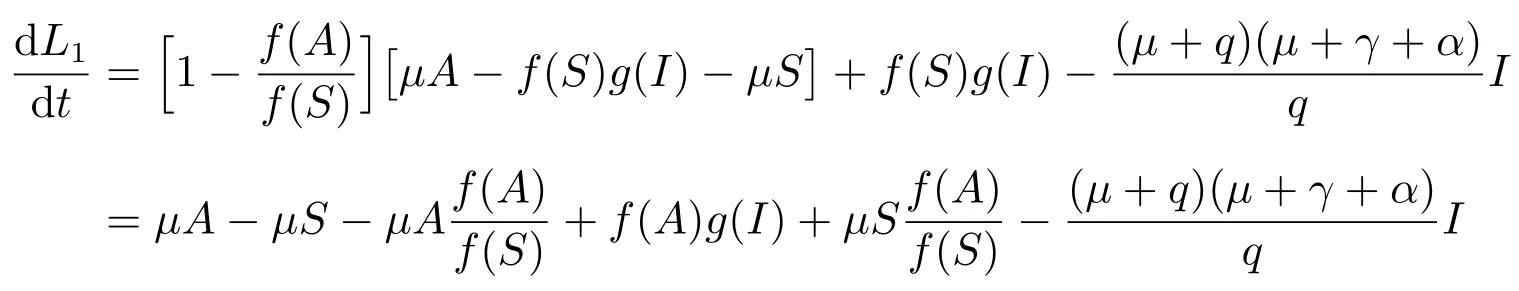
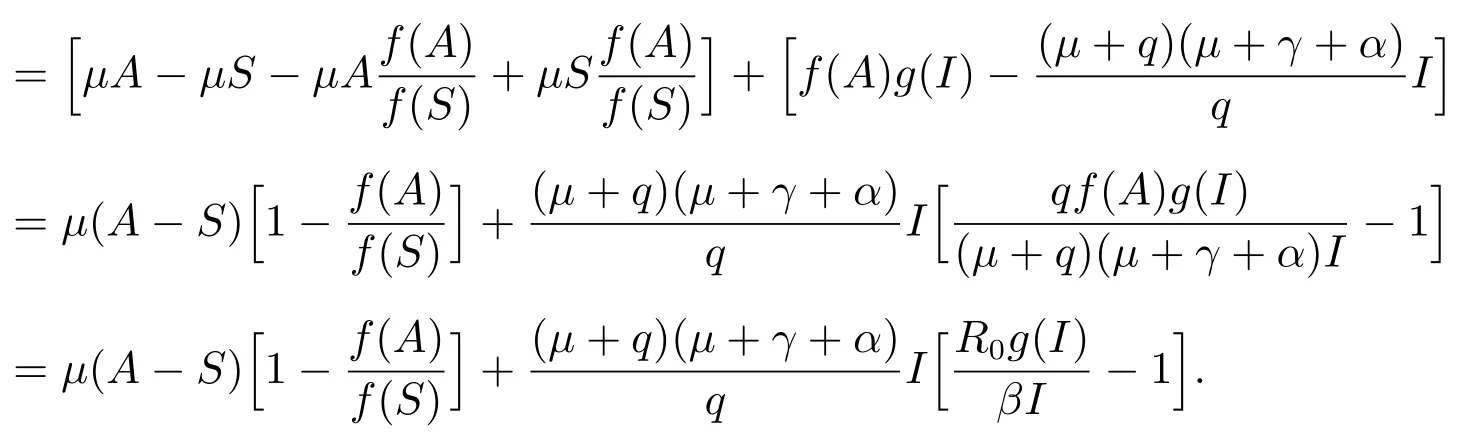
由條件(ii)和(iii)知

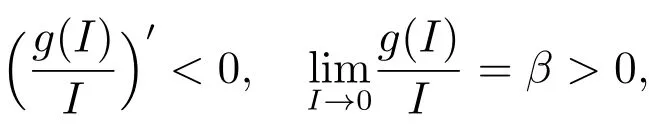
所以

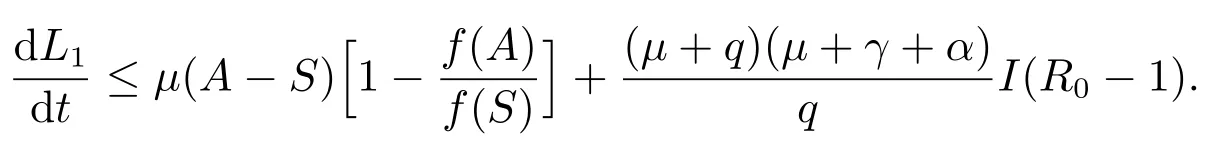
因為對于任意的S＞0，都有所以當S＞0時，

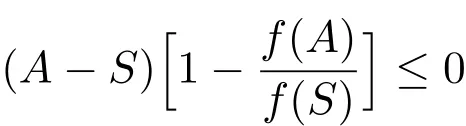
成立.故當時，又因為

所以系統(2)在集合上的最大不變集是單點集

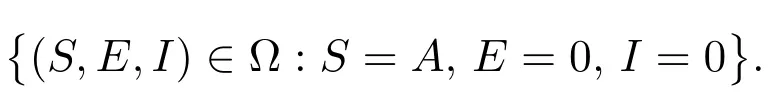
因此，由LaSalle不變性原理[14]可知：當R0≤1時，無病平衡點P0(A,0,0)在集合?上是全局穩定的.

系統(2)在P0處的雅可比矩陣為

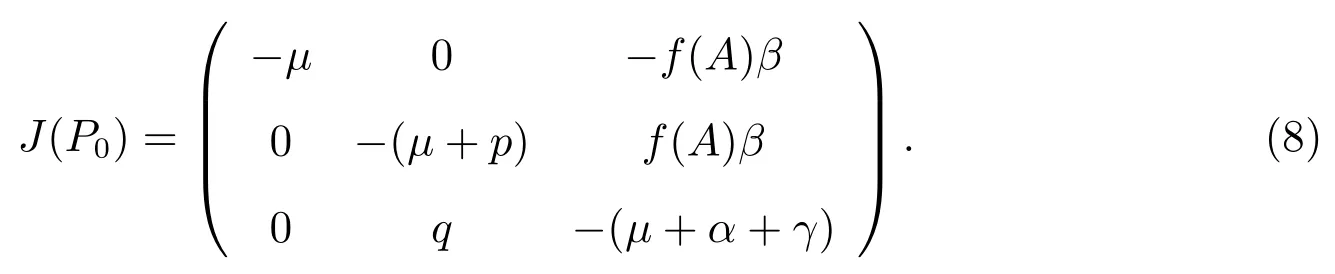
顯然，?μ是矩陣J(P0)的一個負特征根，它的另外兩個特征根分別是如下矩陣的特征根

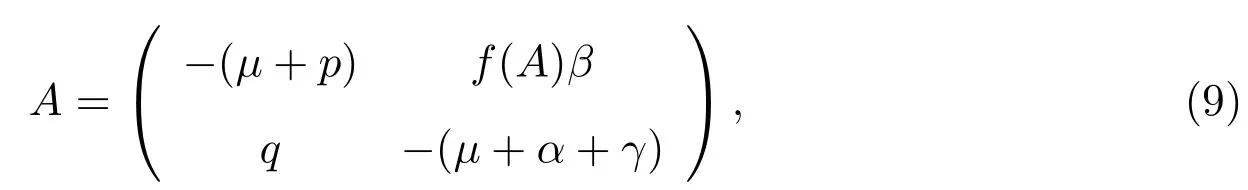
而trA＜0.當R0＞1時，detA＜0，所以矩陣A存在一個正特征值，故當R0＞1時，P0是不穩定的.

本節的第二個結論是：

定理3當R0＞1時，系統(2)唯一的地方病平衡點在?的內部是全局穩定的.

證明 構造如下Lyapunov函數

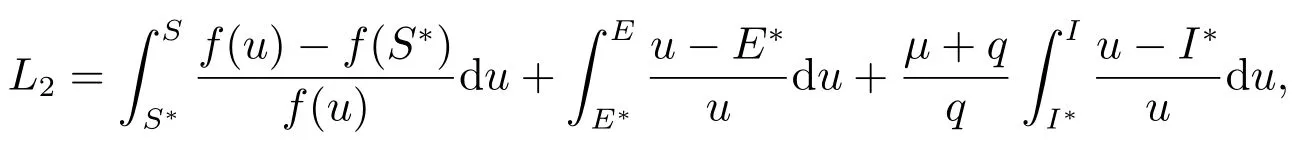
計算L2沿系統(2)解的全導數得

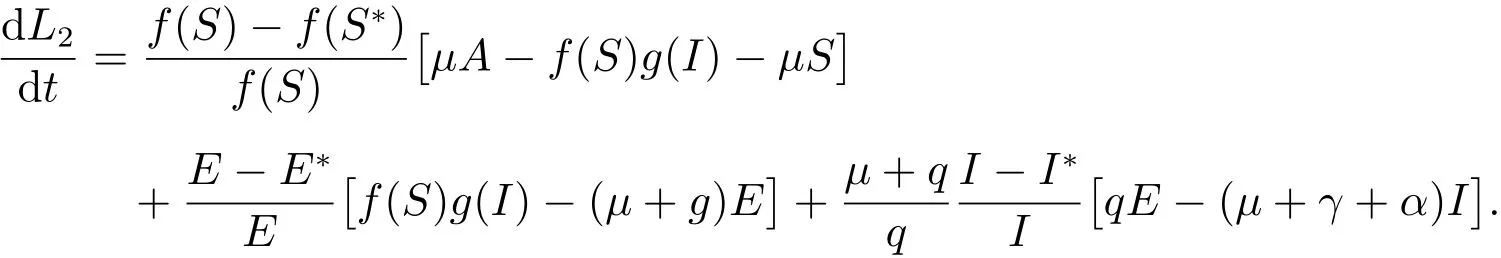
利用(3)可得到

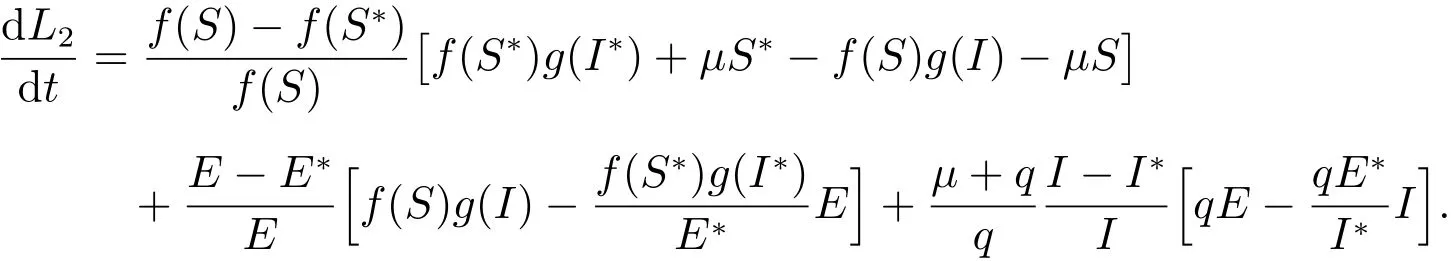
為了書寫簡單，記

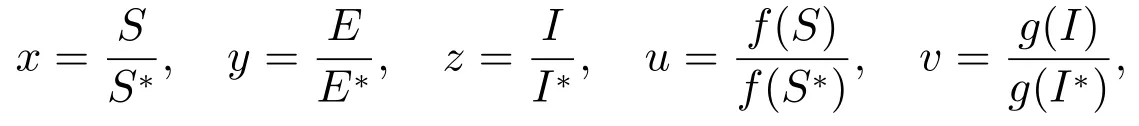
則

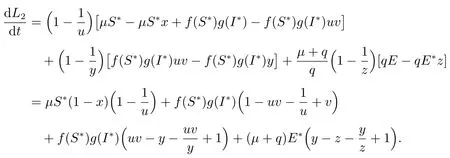
再次利用等式可得

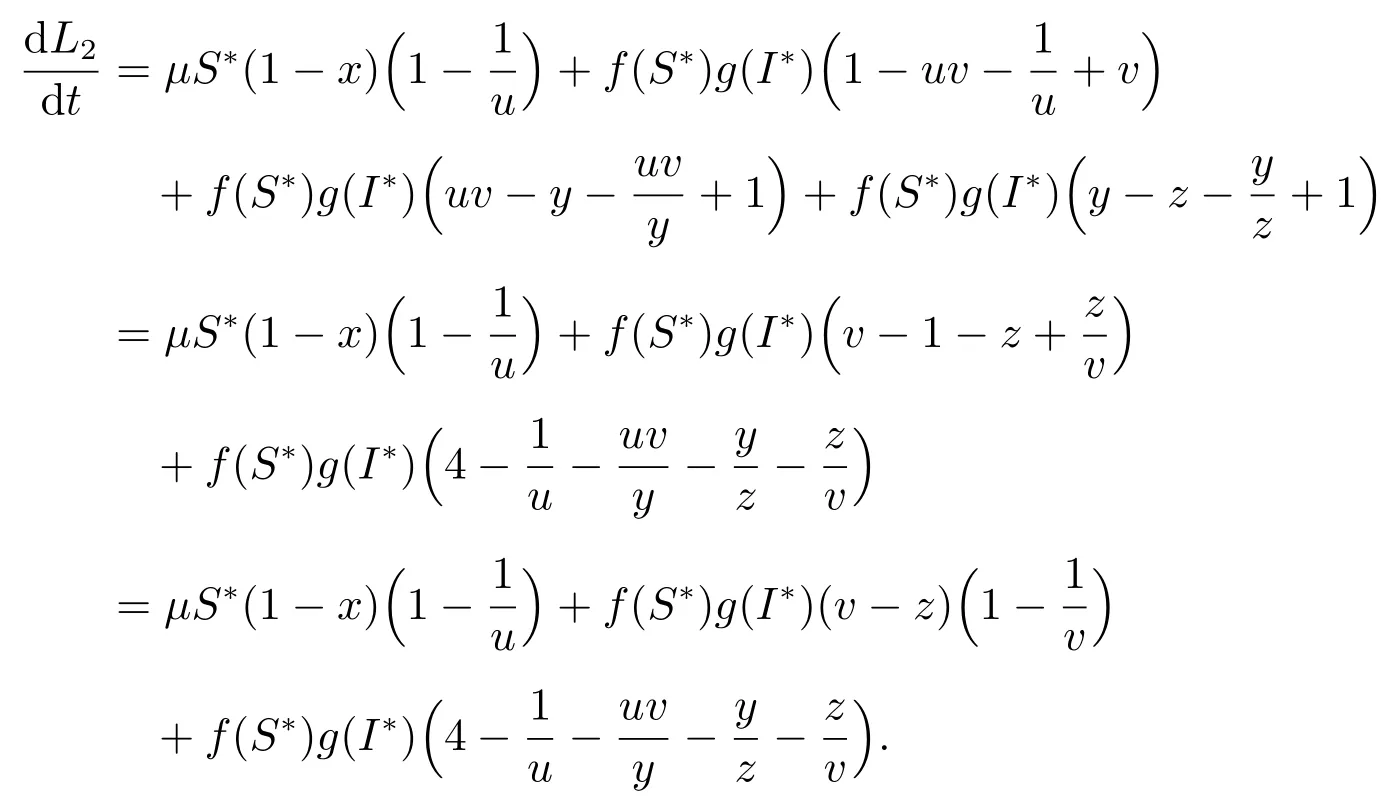
由條件(ii)，可知以下兩個式子成立

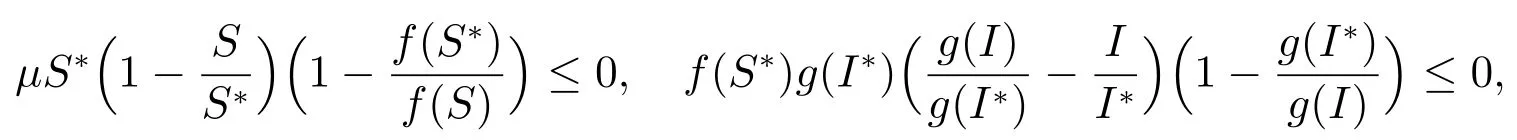
即

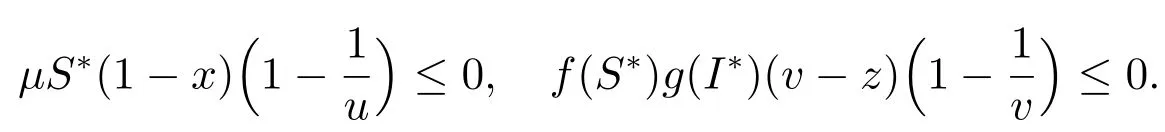
我們知道若干個正數的算術平均數大于或等于它們的幾何平均數，所以

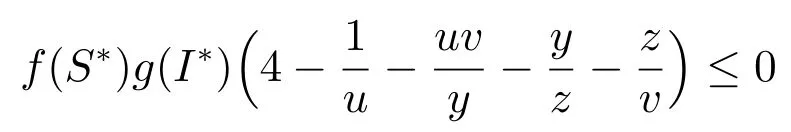
成立.由上可知是負定的，利用李雅普諾夫直接方法[15]可知：當R0＞1時，系統(2)唯一的地方病平衡點在?的內部是全局穩定的.

4 討論

考慮了一類具有非線性發生率的SEIR傳染病模型.利用再生矩陣的方法得到了基本再生數，直接計算得到了平衡點的存在性.通過構造恰當的Lyapunov函數，理論上證明了當R0≤1時，無病平衡點是全局穩定的；當R0＞1時，地方病平衡點是全局穩定的.

為了更直觀的描述系統(2)的平衡點的穩定性，應用Matlab軟件對系統(2)進行數值模擬.不妨取

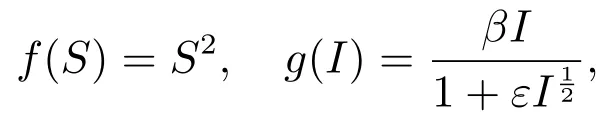
易證f(S),g(I)滿足條件(i),(ii)和(iii)，進一步，選取各參數分別為

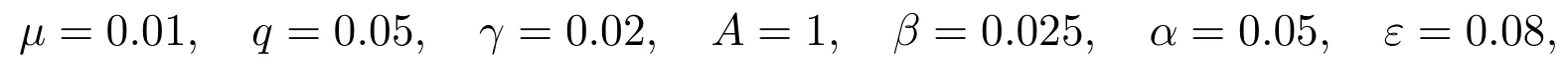
則R0=0.26＜1，此時以三組初值分別為(0.6,0.4,0.3),(0.4,0.5,0.1)和進行數值模擬，如圖1(a).可見當時，三條軌線都趨于同時我們也對應給出了傳染者I(t)的變化曲線，如圖1(b).此時傳染者即疾病最終滅亡.當β值取為0.2，其他參數值和初值不變，則相應的基本再生數再進行數值模擬，如圖2(a).在這種情形下當時，三條軌線都趨于地方病平衡點.同樣，我們也對應給出了傳染者I(t)的變化曲線，如圖2(b).此時傳染者，即形成地方病.這與本文所得定性分析結果一致.這里所用的發生率是已有文獻中不曾見到的.

本文所考慮的非線性發生率是通過對文獻[8–10]中的發生率的歸納、總結、推廣而得到的，具有較好的一般性.我們采用了文獻[12]提出的代數方法成功證明了地方病平衡點的全局穩定性，所以說本文將文獻[12]提出的證明具有雙線性發生率的傳染病模型全局穩定性的代數方法推廣到了更一般地具有非線性發生率的傳染病模型中.

此外，在文獻[16]中，作者假設，顯然，此時條件不再成立.受此啟發，我們將在以后的工作中考慮在沒有條件下，系統(2)的全局穩定性.

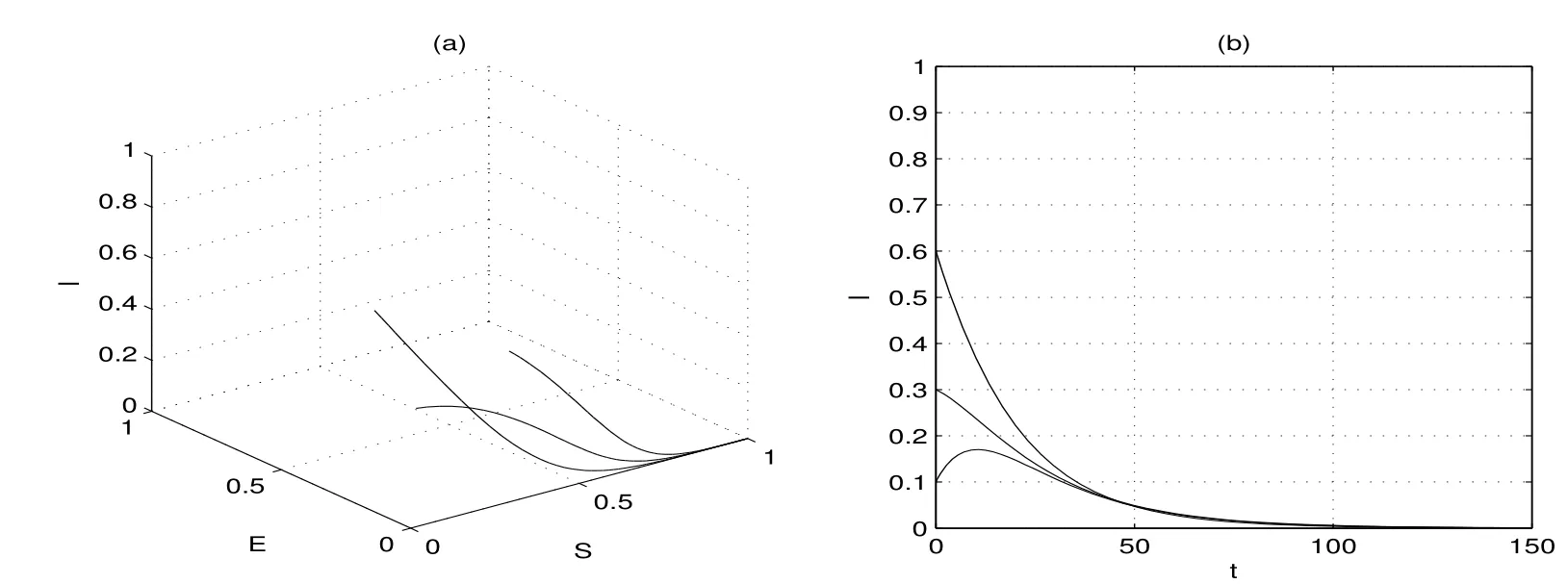
圖1:R0＜1時無病平衡點的全局穩定性

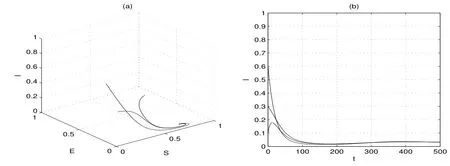
圖2:R0＞1時地方病平衡點的全局穩定性

參考文獻：

[1]Kermack W O,Mckendrick A G.Contributions to the mathematical theory of epidemics,Part I[J].Proceeding of Royal Society of London,1927,A(115):700-721

[2]Anderson R M,May R M.Infectious Diseases in Humans:Dynamics and Control[M].Oxford:Oxford University Press,1991

[3]Min L,Su Y,Kuang Y.Mathematical analysis of a basic virus infection model with application to HVB infection[J].Rocky Mountain Journal of Mathematics,2008,38(5):1573-1585

[4]Li M Y,Muldowney J S.Global stability for the SEIR model in epidemiology[J].Mathematical Bioscience,1995,125(2):155-164

[5]Hethcote H W,Lewis M A,van den Driessche P.An epidemiological model with a delay and a nonlinear incidence rate[J].Journal of Mathematical Biology,1989,27(1):49-64

[6]Liu W M,Hethcote H W,Levin S A.Dynamical behaviour of epidemiological models with nonlinear incidence rates[J].Journal of Mathematical Biology,1987,25(4):359-380

[7]Liu W M,Levin S A,Iwasa Y.Influence of nonlinear incidence rates upon the behaviour of SIRS epidemiological models[J].Journal of Mathematical Biology,1986,23(2):187-204

[8]Li M Y,Muldowney J S,van den Driessche P.Global stability of SEIRS models in epidemiology[J].Canadian Applied Math Quarterly,1999,7(4):409-425

[9]Beretta E,Breda D.An SEIR epidemic model with constant latency time and infectious period[J].Mathematical Biosciences and Engineering,2011,8(4):931-952

[10]李建全，王拉娣，楊友社.兩類含非線性傳染率的傳染病模型的定性分析[J].空軍工程大學學報，2004,5(1):84-88 Li J Q,Wang L D,Yang Y S.Qualitative analysis of nonlinear incidence rate for two epidemic models[J].Journal of Air Force Engineering University,2004,5(1):84-88

[11]Korobeinkov A,Maini P K.Nonlinear incidence and stability of infectious disease models[J].Mathematical Medicine and Biology,2005,22(2):113-128

[12]Li J Q,Xiao Y N,Zhang F Q,et al.An algebraic approach to proving the global stability of a class of epidemic models[J].Nonlinear Analysis:Real World Applications,2012,13(5):2006-2016

[13]van den Driessche P,Watmough J.Reproduction numbers and subthreshold endemic equilibria for compartmental models of disease transmission[J].Mathematical Biosciences,2002,180(1):29-48

[14]LaSalle J P.The Stability of Dynamical Systems[M].New Jersey:Hamilton Press,1976

[15]Verhulst F.Nonlinear Differential Equations and Dynamical Systems[M].Berlin:Springer-Verlag,1996

[16]Kar T K,Batabyal A.Modeling and analysis of an epidemic model with nonmonotonic incidence rate under treatment[J].Journal of Mathematical Research,2010,2(1):103-115