采用階躍函數分析經歷地震的大壩安全監測數據

陳　容，冉　蠡，楊　杰，程　琳

(1.大唐碧口水力發電廠，甘肅省文縣　746412；2.西北旱區生態水利工程國家重點實驗室培育基地，西安　710048)

?

采用階躍函數分析經歷地震的大壩安全監測數據

陳容1，冉蠡2，楊杰2，程琳2

(1.大唐碧口水力發電廠，甘肅省文縣746412；2.西北旱區生態水利工程國家重點實驗室培育基地，西安710048)

摘要：大壩經歷大地震后，壩體位移監測數據會發生明顯突變。利用傳統統計模型對監測數據進行建模，擬合程度較低、效果較差。為此，將階躍函數引入傳統統計模型中，重新構建回歸分析模型。以碧口大壩豎向位移監測數據資料為例，分別采用傳統統計模型和階躍函數模型進行逐步回歸分析，并利用階躍函數監測模型分離地震分量，通過分析地震對大壩豎向位移的影響規律，以驗證階躍函數模型的優越性。分析結果表明，階躍函數模型的擬合精度及預測效果均高于傳統模型，可供類似工程參考。

關鍵詞：大壩監測；階躍函數；地震突變；逐步回歸分析；地震分量；統計模型

0前言

大壩安全監測是對水利工程相關結構、設施及周圍環境通過儀器監測或人工巡視所做的測量及觀察。而所得到的相關數據及其變化是對大壩運行情況的真實反映。因此，真實、準確地分析監測數據對于確定大壩運行狀態與大壩安全鑒定有著重要意義。大壩監測數據在遭受地震等自然災害后，由于地震荷載作用或儀器損壞而出現突變點，給建立大壩安全監測模型與數據回歸分析增加了難度，使得傳統統計模型對大壩監測數據的回歸分析結果與實測值的擬合效果較差，進而不能較好地體現出各影響因子對效應量的影響程度。此情況表明，傳統統計模型不適用于經歷地震的大壩監測數據，需要重新建立新模型。鑒此，本文基于傳統統計模型，運用單位階躍函數構建出大壩安全監測數據回歸分析的階躍函數監測模型，并將該模型運用于碧口大壩監測數據的回歸分析中。通過與常規模型相比，證明階躍函數監測模型具有精度高、擬合效果好、能較好地反映各影響因子與效應量間的關系等優點。

1單位階躍函數

單位階躍函數具有許多特性，若一般函數能用它表示出來，那么對研究問題或運算將十分有益。

階躍函數定義為：

(1)

式中：uA為階躍函數；t、t0分別為變量；A為常數。

函數圖像如圖1所示。

圖1　階躍函數圖像圖

當常數A=1時，式(1)為單位階躍函數，記作：

(2)

利用階躍函數，將分段函數用1個函數來表示[1-2]。如分段函數：

(3)

式中：f1(t)和f2(t)分別為[0，t0]和[t0，+∞]上的連續函數，則有：

(4)

2土石壩位移監測模型

2.1傳統統計模型

影響大壩壩體豎向位移的主要因素有庫水壓力、溫度變化和時效等，因此，豎向位移由水壓分量δH、溫度分量δT和時效分量δθ組成，即：

(5)

作用在壩體的靜水壓力，與壩體在水壓荷載下的因滲流影響產生豎向位移，是水壓荷載對大壩豎向位移作用的2個主要方面。由于滲流的產生時間相對于庫水位的變化時間具有滯后性，所以水壓因子的取值為測點在監測日前1～3 d、4～10 d、11～30 d、31～60 d所對應的上游庫水位的平均值。水壓分量δH表示為：

(6)

因為氣溫為周期性變化，因此溫度分量用正弦函數與余弦函數的周期項來表示。溫度分量δT為：

(7)

式中：t為監測日至監測基準日的累計天數；t0為第1個測值日至監測基準日的累計天數；b1i、b2i分別為溫度因子回歸系數。

選擇時效分量δθ表達式為：

(8)

式中：θ為監測日至監測基準日的累計天數除以100；θ0為第1個測值日至監測基準日的累計天數除以100；c1、c2分別為時效因子回歸系數[3]。

通過上述分析得出，大壩豎向位移的統計模型如下：

δ=δH+δT+δθ+a0

c1(θ-θ0)+c2ln(θ-θ0)+a0

(9)

式中：a0為常數項。

2.2基于階躍函數的大壩豎向位移監測模型表達式

為提高監測模型精度與擬合效果，使之能較好地模擬監測資料的突變和波動變化，并能正確地反映出各影響因子與效應量間的關系，故在傳統統計模型基礎之上引入單位階躍函數，以進行擬合修正[4-7]。單位階躍函數主要用于修正傳統統計模型中的時效分量，修正后的豎向位移監測模型為：

δ=δH+δT+δθ+a0

(10)

2.3突變點判定

在實際監測數據中，地震與觀測誤差均能使監測數據產生突變。地震引起的突變是由于地震荷載作用或儀器損壞而致，雖突變后監測值較突變前監測值呈整體增大或減小，但測值變化仍可正確反映所監測項目的真實性態；觀測誤差是由于觀測者主觀疏忽或外界客觀因素影響，使個別監測數據較其前后測值呈突然增大或減小。存在觀測誤差的監測值屬于錯誤的監測數據，其不能正確地反映出監測項目的真實性態，應對其進行剔除。一般用來剔除監測數據系列中觀測誤差的方法有：格羅布斯準則、狄克松準則、肖維勒準則、羅曼諾夫斯基準則、3σ準則等，其中3σ準則是最簡單、最常用的處理觀測誤差的方法[8-9]。

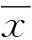
3實例

3.1工程及監測概況

位于甘肅省文縣碧口鎮的碧口水電站是白龍江干流上最早開發的梯級電站。此工程布置了較為全面的監測措施，其中，土石壩的豎向位移監測為主要監測項目之一。在施工期，用于監測豎向位移的15支沉陷監測管，分別布置在壩身的3個斷面、深墻頂、寬墻等部位。但到1974年底，這些監測管全部損壞。大壩竣工后，分別在原壩體上下游7個縱斷面上又增設多個橫斷面監測點，共布設了47個測點以監測大壩豎向位移。從施工結束后至1977年9月開始起測時，有47個大壩豎向位移測點可以監測，隨著設備失效老化、地質活動等原因，其中部分測點儀器已經損壞，但經過不斷修繕，到目前仍在進行監測的測點有42個[12-13]。測點標號及位置見圖3。對這42個測點的監測數據資料，分別建立傳統統計模型和階躍函數模型進行逐步回歸分析，并對模型計算結果進行對比分析。

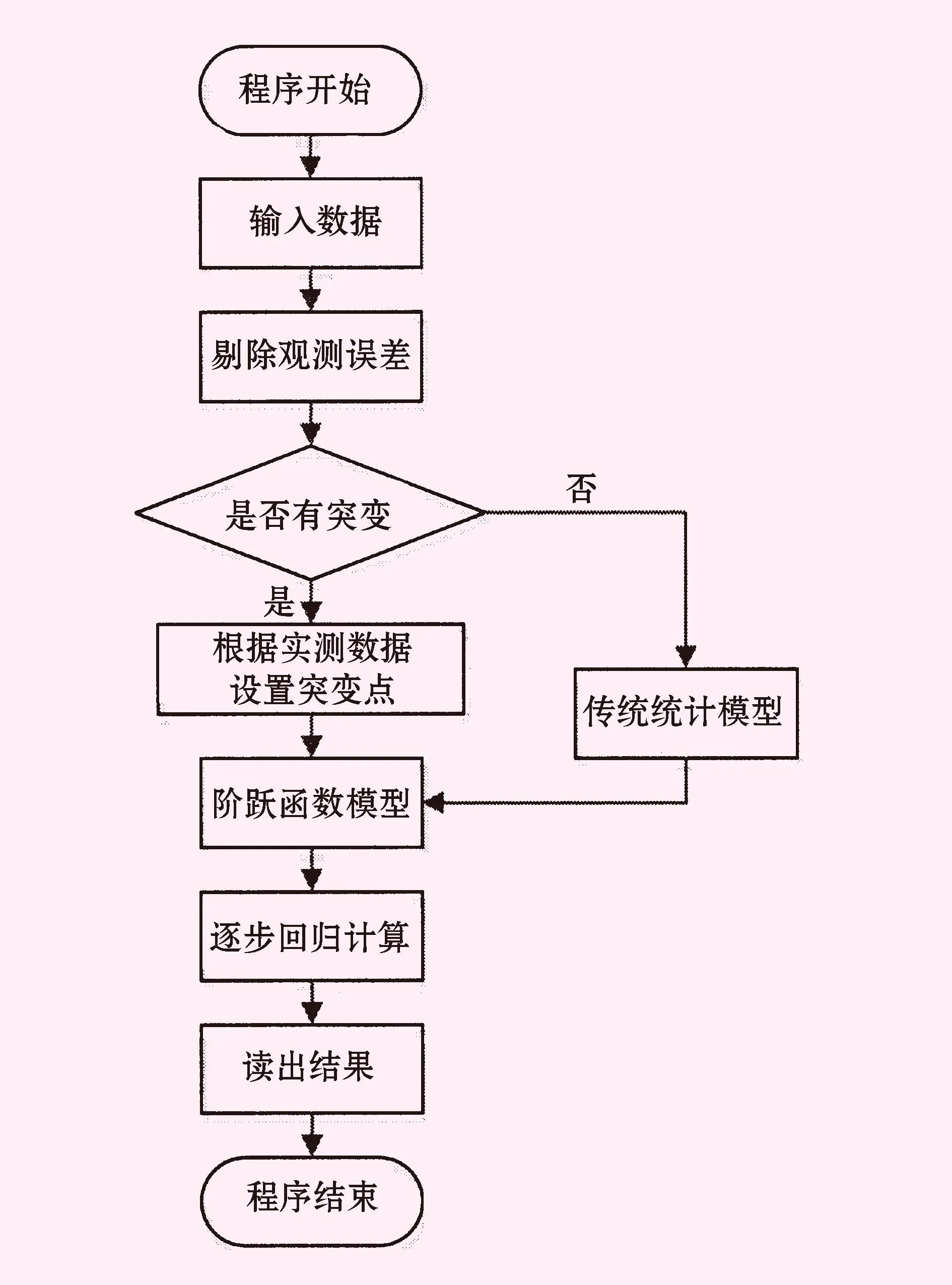
圖2　回歸計算流程圖

3.2回歸計算分析

現以大壩壩體D9-1測點的豎向位移監測資料為例，觀測資料時間序列為1995年1月7日至2014年12月9日，此期間監測資料因2008年5·12地震和地震后監測儀器的修復和升級改造而出現突變點。建立傳統模型、分段模型和階躍函數模型，利用matlab軟件分別進行逐步回歸分析，以檢驗階躍函數模型的分析效果。其中，分段模型是利用傳統模型在數據突變處兩側分別建模。階躍函數模型中分別設置2008年5月13日和2009年1月8日為數據突變點。

利用式(9)、(10)對測點D9-1的豎向位移監測數據進行回歸計算。復相關系數R、剩余標準差S與顯著水平F見表1，圖4所示是對測點進行3種回歸模型計算的實測值與擬合值過程線。

表1　2種模型回歸分析參數對比表

由表1可看出，階躍函數監測模型的復相關系數(0.993)大于傳統統計模型的復相關系數(0.885)，傳統統計模型剩余標準差(41.2)大于階躍函數監測模型剩余標準差(10.3)。采用傳統模型進行分段建模的復相關系數分別為0.999、0.628，兩者復相關系數相差較大、擬合效果不穩定，同時剩余標準差分別為11.7、17.2，兩者均大于階躍函數監測模型。當數據資料突變點較多時，進行分段建模分析的工作量會大大增加，效率降低。由此可知，階躍函數監測模型的精度和運行效率高于傳統模型。

圖3　碧口大壩監測布置圖

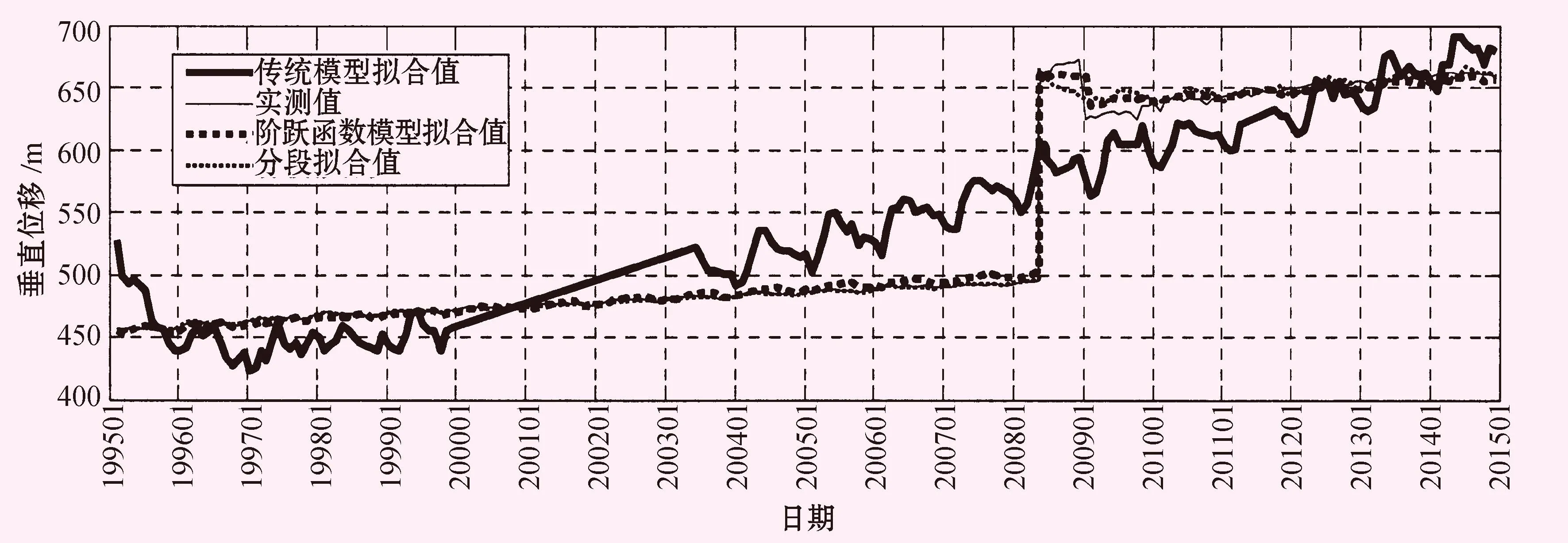
圖4　3種模型回歸分析后的擬合值與實測值過程線圖

由圖4可看出，在2008年5月13日和2009年1月8日這兩處監測數據發生突變的時間點前后，階躍函數監測模型的擬合值比傳統模型的擬合值更接近實測值。與分段建模相比較，階躍模型與分段1的擬合程度相似；在分段2處，階躍模型的擬合值更接近實測值。由此可見，階躍函數監測模型的擬合效果好于傳統模型和分段建模，擬合值更為接近實測值。

3.3地震效應分離與大壩豎向位移變化速率分析

大壩在經歷地震后，地震分量在時效分量中占有絕大比重。從時效分量中分離出地震分量，通過分析地震分量大小可得出地震效應對大壩各部分的影響情況。現對大壩下游0+041.80 m(下游縱斷面)，壩左0+224.00 m(最大橫剖面)，0+304.00 m(岸坡橫斷面)3個斷面的測點擬合值分離地震分量，分離出的地震分量見圖5～7，大壩位移變化速率見表2。

圖5下游縱斷面(0+041.80 m)各測點地震分量　單位：mm

圖6最大橫斷面(0+224.00 m)各測點地震分量　單位：mm

圖7岸坡橫斷面(0+304.00 m)各測點地震分量　單位：mm

由圖5可看出，各測點的地震分量并不相同，表明地震對大壩各部分的影響不同。在圖5所示斷面中，在大壩中部D10-3測點處的地震分量最大，向兩岸壩肩方向的測點地震分量依次減小。表明地震對大壩中部河床壩段的影響大于岸坡壩段，越靠近兩岸的壩體，地震對其影響越小。在圖6、7所示橫斷面中，大壩中部靠近壩頂處的測點的地震分量大于下游壩段，越往下游地震分量越小。表明地震對大壩壩頂處的影響大于下游壩坡，且越靠近下游的壩體，地震對其影響越小。此分析結果符合以往土石壩地震模擬試驗的相關結論[14-16]。

表2　大壩豎向位移變化速率表　mm/a

由表2可看出，地震時因地震荷載作用，壩體部分土體液化或松動而不穩定。在地震后的幾年中，大壩土體在自重和水壓力等作用下重新穩定，即地震后大壩豎向位移變化速率較地震前明顯加快，之后速率逐年遞減，隨時間推移而趨于平穩。

3.4結果分析

由上述分析可知，相較于傳統統計模型，階躍函數監測模型的精度高、擬合效果好。且通過模型分離的地震分量，分析得出地震(影響因子)對于大壩各部分豎向位移的影響程度(效應量)關系相同于以往的相關實驗結論，即符合土石壩壩體豎向變形的一般規律。表明在分析經歷地震的大壩監測數據中，階躍函數監測模型較傳統模型具有先進性、客觀合理性。可用該模型對因地震等自然災害或其他原因而產生突變的監測資料分離各分量，進而進行定量分析。

4結語

以碧口大壩監測資料為例，在傳統統計模型中引入單位階躍函數，修正為階躍函數監測模型。同時建立傳統統計模型和階躍函數監測模型，利用matlab軟件分別進行逐步回歸分析，比較兩者模型精度與擬合效果，并運用階躍函數監測模型分離出地震分量，以分析地震對大壩豎向位移影響性態。分析結果表明，階躍函數監測模型回歸分析效果遠優于傳統統計模型，回歸計算參數更為合理、擬合效果好，計算分析成果符合相關實驗規律，可供類似監測項目參考使用。

參考文獻:

[1]李祖斌,黃淑貞.一般函數的單位階躍函數表達式[J].集美航海學院學報,1994,12(1):71-74.

[2]田社平,陳洪亮,李萍.階躍函數的定義及其在零點的取值[J].電氣電子教學學報,2005,27(2):38-40.

[3]陳德平,韓云峰,雷劍,等.碧口土石壩豎向位移監測的逐步回歸模型擬合與分析[J].西北水力發電,2006(22):142-145.

[4]楊金凱,包騰飛,朱凱,等.棉花灘碾壓混凝土重力壩裂縫計階躍函數監控模型[J].水電能源科學,2013,31(10):67-69.

[5]徐波,程琳,荊凱.巖灘大壩鋼板計階躍函數監控模型[J].水電能源科學，2010,28(2):75-77.

[6]陳龍.溢流壩段水平位移混合模型的建立[J].大壩與安全，2003(01):60-62.

[7]李錚,李宏恩,袁啟旺,等.階躍函數模型在龍江水電站壓力鋼管監測中的應用[J].水電能源科學，2011,29(7):97-100.

[8]熊艷艷,吳先球.粗大誤差四種判別準則的比較和應用[J].大學物理實驗，2010,23(1):66-68.

[9]梁曉紅. 軋輥測量數據粗差剔除的3σ應用研究[J].科技信息，2006(12):66-68.

[10]許貝貝,崔晨風.大壩自動化監測數據粗差處理方法研究[J].測繪地理信息，2015,40(2):59-61.

[11]覃欣,熊娟.LabVIEW數據處理中3σ準則的應用[J].中國測試，2009,35(5):66-69.

[12]陳容,劉林.震后碧口大壩安全監測資料分析[J].大壩與安全，2011(03):43-46.

[13]朱晟,石高峰,周建平.碧口心墻堆石壩抗震復核分析[J].巖石力學與工程學報，2011，30(增1):2954-2962.

[14]陳寧,楊正權,袁林娟,等.兩河口水電站高土石壩地震反應地震模擬振動臺模型試驗研究[J].水利水電技術,2010,41(10):80-86.

[15]楊正權,劉小生,汪小剛,等.高土石壩地震動力反應特性大型振動臺模型試驗研究[J].水力學報,2014,45(11):1361-1372.

[16]劉福海. 土石壩地震破壞機理振動臺試驗研究[D].大連：大連理工大學，2012.

Analysis on Safety Monitoring Data of Dam Experiencing Earthquake by Step Function

CHEN Rong1, RAN Li2, YANG Jie2, CHENG Lin2

(1. Datang Bikou Hydropower Plant, Wenxian, Gansu746412, China;2. State Key Laboratory Base of Eco-Hydraulic Engineering in Northwest Arid Area, Xi'an710048, China)

Abstract:After dam experiences earthquake, the monitoring data of the dam body displacement will change promptly and obviously. The fitting is lower in degree and the result is poor in quality provided that the traditional statistic model is applied for building the model of the monitoring data. Therefore, the step function is introduced into the traditional statistic model and the regression analysis model is re-built. With the case of the monitoring data of the vertical displacement of Bikou dam, both the traditional statistic model and the step function model are applied for the stepwise regression analysis as well as the step function monitoring model is utilized to separate the earthquake component. Through analysis on the influence law of the earthquake to the vertical displacement of the dam, the superiority of the step function model is verified. The analysis demonstrates that the fitting precision and forecast effect of the step functional model both are higher than those of the traditional model. It provides similar projects with reference.

Key words:dam monitoring; step function; earthquake prompt change; stepwise regression analysis; earthquake component; statistic model

中圖分類號：TV698.1

文獻標識碼：A

DOI:10.3969/j.issn.1006-2610.2016.02.021

基金項目：國家自然科學基金(51409205)；陜西省創新研究計劃(2013KCT-15)

作者簡介：陳容(1981- )，女，四川省隆昌縣人，工程師，從事大壩運行管理工作.

收稿日期：2016-02-02

文章編號：1006—2610(2016)02—0080—05