例談思想方法在數學復習中的滲透

周東

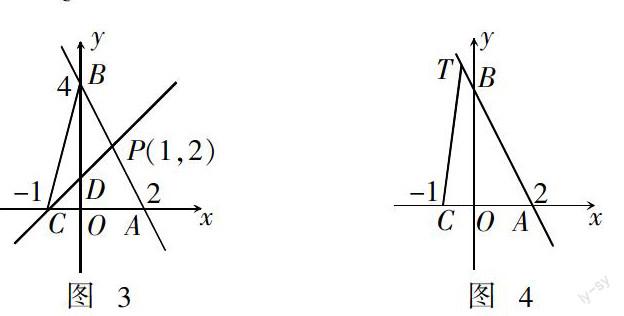
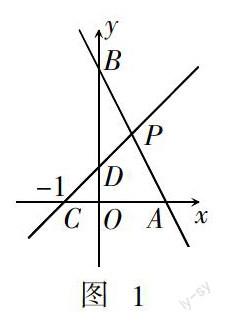
【摘要】初中數學復習課不能只停留在講一題是一題的層面，要進一步提煉數學思想方法，培養學生用思想方法解題的能力，從而達到觸類旁通的效果. 本文從八上復習《一次函數與三角形的面積》一課設計為例，談在數學課堂上滲透數形結合、轉化、分類討論的思想方法.

【關鍵詞】 數學；思想方法

當前，初中數學復習課堂多以解題教學為主線，解了一題又一題. 教師爭取課堂密度大，多講習題，學生也想把這些習題都聽懂，這樣的課堂學生忙教師苦，走進了數學教學的誤區. 筆者認為在數學復習課教學中要對數學內容的進一步提煉和概括，總結出相對應的數學思想方法，數學思想方法是對數學內容的一種本質認識，有了數學思想為靈魂，數學才有了魅力. 因此，在復習時要注重體會教材例題、習題以及中考試題中所體現的數學思想和方法，培養用數學思想方法解決問題的意識.下面以八上期末復習《一次函數與三角形面積》為例，談數學復習課堂如何注重培養學生數學思想與方法.

一、課前梳理，數形結合

著名數學家華羅庚說過：“數缺形時不直觀，形少數時難入微”. 所謂數形結合是指抽象的數學語言與形象直觀的圖形結合起來，從而實現由抽象向具體轉化的一種思維方式. 八上學生第一次接觸函數存在一定的難度，筆者在課前梳理階段做了如下設計，讓學生獨自完成體會數形結合思想.

1. 點A（3，-2）到x軸的距離是______，到y軸的距離是_______.

2. 直線y = -2x + 4與x軸交點A坐標______，與y軸交點B坐標______，△AOB的面積是______.

3. 直線y = -2x + 4與y = x + 1相交于點T，則點T的坐標為______.

4. 已知A（ 2， 0 ）、C （ -1，0），則AC = ______.

歸納：

1. 點P（a，b）到x軸的距離為______，到y軸的距離為______ .

2. 一次函數y = kx + b與x軸的交點坐標______，與y軸的交點坐標______.

3. 通過解方程（組）求交點坐標.

4. 點A（a，0）點B（b，0），A、B兩點之間的距離為_____.

通過練習，讓學生感受點的坐標一對有序實數和點的位置的關系，點的坐標到坐標軸距離之間的關系，為課堂學習打好基礎.

二、層層深入，化繁為簡

轉化思想是解決數學問題的一種最基本的數學思想，在研究數學問題時，我們通常是將未知問題轉化為已知的問題，將復雜的問題轉化為簡單的問題，從而提高同學們的解題能力. 在課堂復習中筆者設計如下幾個環節：

（一）知識應用

如圖（1），直線l：y = -2x + 4與x軸、y軸分別交于點A、B，直線y = x + 1與x軸、y軸分別交于點C、D，與直線l交點P.

（1）求△CAP的面積.

（2）你還能求出哪些三角形的面積？

（3）連接BC，求△BCP的面積.

讓學生探索：有邊在坐標軸上的三角形，利用在坐標軸上的（或平行于坐標軸）的線段為底. 第三問△BCP沒有邊在坐標軸上怎么辦？利用割補法將三角形面積轉化為有邊在坐標軸上的（或平行于坐標軸）三角形面積和（差）.

（二）知識拓展

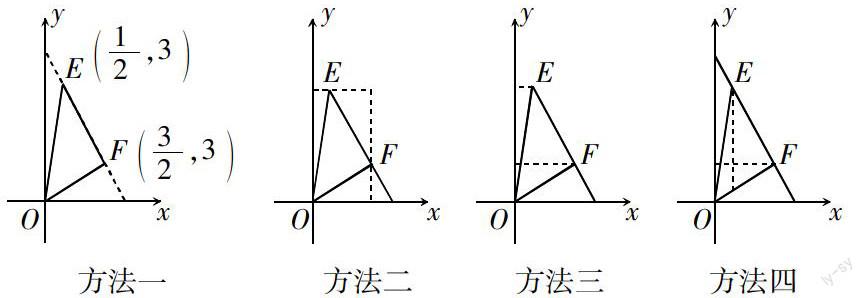
拓展一 如圖，在直線y = -2x + 4上，取兩點E（1/2，3），點F（3/2，3），求△EOF的面積（多種方法）.

通過充分的討論交流，讓學生概括總結求三角形面積的多種方法. 點撥概括：割補法可以將三角形面積轉化為面積和或差，即向內分割和向外補形.

拓展二 如圖（3）點Q在y軸上，且△QPB與△CPB面積相等，求點Q的坐標.

同樣的問題背景，在求了三條直線圍成的靜態的三角形面積后，筆者設計了在y軸上的一個動點和原三角形面積相等問題，注重培養分類討論的數學思想.

拓展三 如圖（4），點T是直線AB： y = -2x + 4上的一個動點，連接CT.設T點橫坐標為t.

（1）求△CAT的面積S與t的函數關系.

（2）當點T運動到什么位置時△CAT的面積為6.

把動點從坐標軸上改成在直線AB上，靜態的三角形變成一個動態的三角形，面積就變成了一個函數問題，促進學生對動態問題的研究思維的形成.

三、課后小結，總結提煉

讓學生概括本節課復習的三角形面積求法：有邊在坐標軸的（或平行于坐標軸）的三角形，找在坐標軸上的邊為底，用三角形的面積公式求；沒有邊在坐標軸的用割補法，求幾個圖形的面積和或差. 本節課所體現的數學思想：數形結合、轉化思想、分類討論. 在課后小結中要注重思想方法的提煉小結，從而培養學生用思想方法解題的能力.