多邊形內角和定理適用性討論
2016-05-30 10:04:19金震宇
數學學習與研究 2016年10期
金震宇
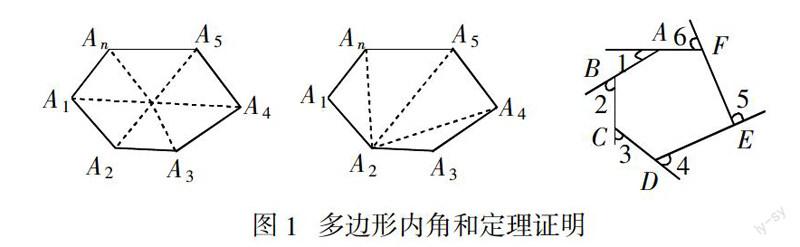

一、前 言
多邊形內角和定理為:n多邊形內角和 = (n - 2)180°,n多邊形外角和 = 360°,其證明源于三角形內角和 = 180°. 如圖1所示,在凸多邊形中借助輔助線引入適量三角形,使原多邊形內角和轉化為引入諸三角形內角和,從而得證. 其證明細節請參看文獻[1].
因為凸多邊形一個頂點對應一條邊,所以可數它有多少暴露出的頂點數求出較復雜凸多邊形邊數. 但是我在做題中發現,有類問題無論是數邊還是數頂點求出的結果都出錯. 這引起我興趣,故寫出來與大家討論.
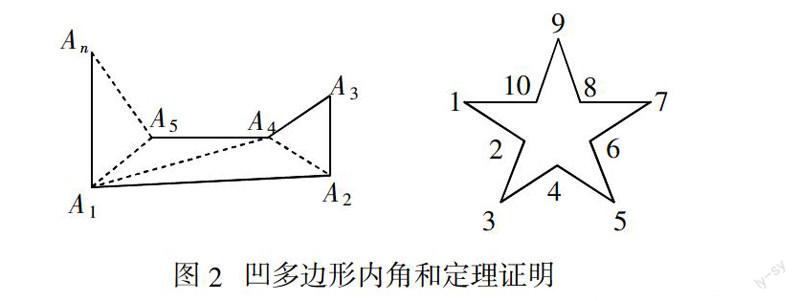
二、多邊形內角和定理僅適用于凸多邊形和凹多邊形
三、多邊形內角和定理不適用于出現交叉線的多邊形
請先看圖3左圖,這是有交叉線四個頂點最簡單圖形,若用多邊形內角和定理,其內角和為360°. 這顯然不是角∠A + ∠B + ∠C + ∠D之和,題中多算了∠1 + ∠2,而∠1或∠2的具體數值不確定,僅據 ∠1和∠2為對頂角,可已得到:∠A + ∠B = ∠C + ∠D,故∠A + ∠B + ∠C + ∠D之和無解.
四、結 論
多邊形內角和定理僅適用于凸多邊形和凹多邊形,它不適用有交叉線圖形,解題時若遇到有求交叉線圖形求多角和時,要依平面兒何諸定理知識,設法把問題轉化為求凸多邊形或凹多邊形內角和,使問題得解.
【參考文就】
[1]數學,七年級下冊[M].江蘇科學技術出版社,2012年11月第3版,P31-35.
[2]學習與評價,數學測試卷,七年級下,第7章[M].江蘇鳳凰出版社.

