初中數學教學中學生的發散思維培養的意義與方法
◎丁偉偉
(豐縣范樓鎮范樓初級中學,江蘇 豐縣 221700)
初中數學教學中學生的發散思維培養的意義與方法
◎丁偉偉
(豐縣范樓鎮范樓初級中學,江蘇 豐縣 221700)
學生對事物的推理能力,是數學課程應該讓學生學會的簡單技能.“解決問題”必須用到數學中發散思維,而關于事物的推斷能力的養成和拓展創新也需要數學發散思維.在教育教學中,讓學生養成發散思維是教學的一個重點.那么,應該怎樣合理讓學生養成發散思維?本文在分析培養學生的發散思維的意義之后,闡述了兩種培養學生發散思維的方法,希望對初中數學教學有一定借鑒意義.
初中數學;教學;散性思維;培養
一、初中數學教學中學生的發散思維培養的意義
培養學生的發散思維,有利于數學教師為學生營造良好的學習氛圍,從而提高教學效率.老師帶著學生這樣學習,可以讓學生在課堂上思維更活躍,從而有利于教學效率的提高.有意學習和無意學習相互融合,能為學生和老師開創和諧流暢的教育環境,進而贏得良好的教學效果.
重視發散思維,并且將發散思維在數學教學中運用,可以讓學生對數學知識的認識面更全面,進而了解各個知識之間的關系.學生學習能力的提高有賴于思維的連貫性.通過更多角度的思考、更多的方式解決問題,學生的思維可以得到很好的提高.學生迅速地從各方面和切入點對一個問題進行解決,這樣學生對知識的理解便會從“知識點”發展到“線和面”直到全部的數學知識.[1]
二、初中數學教學中學生的發散思維培養的方法
(一)通過問題類比法,培養學生發散思維
在數學活動的參與過程中,能主動讓積極思維參與到教學活動中去,并高度參與問題的解答過程,這就是思維的積極性的體現.學生對于學習的熱情度,是他們思維活動的最有力、最有用的推進力.
例如:假設有一個平面,這個平面最多能被10條直線劃分成多少部分?
學生肯定對這種題目很沒有興致,但是當老師改編一下題目,例如,假設有一個圓形的蛋糕,現在要求切十刀,切的時候不能對折,最多可以得到幾塊蛋糕.面對生活中經常遇到的場景,這時候學生產生了做題的興趣.同時,“先退后進”的解題方法在此時利用,效果最佳.
問:如果只切一刀,可以得到幾塊蛋糕,如果切2刀,最多可以得到幾塊蛋糕?如果切3刀,最多可以得到幾塊蛋糕?那么類推后,把得到的數進行分解可以解出2=1+1(切一刀時),4=1+1+2(切二刀時),7=1+1+2+3(切三刀時),進而讓學生發現得到的塊數在數量上與兩組數的和相等,所以,切了幾刀,最后一個切數就等于幾,進而得出結論,當在蛋糕上切10刀時,最多可得到餅的塊數是S10=1+1+2+3+…+8+9+10=56,這樣就可以推導出,平面最多能被10條直線劃分成56部分.
在老師這種教學方式下,再難懂的問題也可以被輕松解決,就算是有更多的直線去切割平面,學生的思維得到了拓展,問題自然可以被學生輕松解答了.
這樣可以得出結論,在教授數學科目時,利用新方法或者改變問題的單調性,是讓學生養成創新能力和營造好的環境的有效方法,這樣可以讓學生的創新能力得到激發,更多的創新空間和自主發展時間有利于體現學生在教學過程中的主體地位.
(二)例題設計開放化,培養學生發散思維
完成強化學生三維教學目的是新課程的理念,老師可以根據學生的知識水平特點和生活經歷提出精妙的問題,開放性的例題設置,對學生的思維提升和教學質量的提升都有好處,同時還可以培養學生的發散思維.[2]
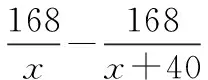
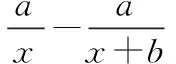
對結論的隱藏或者開放,還有置換結論和數據,都可以作為改編例題的方式.各種方法都可以讓原來呆板的題變得栩栩如生,讓學生感受到這個課堂的魅力,教與學的整體課堂變得和諧,讓“教為主導,學為主體”的思想表現得淋漓盡致.
三、結 語
對學生發散性思維能力的訓練是教師工作的關鍵點,這可以打破慣性思維的狹窄目光,根據改編、拓展、解答、聯系,可以讓學生的思維能力在數學學科中得到很大的提高,進而能挖掘或創新出多的數學問題解答方式.教學過程中注重學生發散性思維能力的提升,有利于培養出更多的適應時代發展的創新型人才.
[1]孫興權.新課標下高中數學效率課堂實施策略[J].動畫世界:教育技術研究,2012(7).
[2]高麗.高中數學教學效率的提高[J].現代教育科學:中學教師,2011(6).

