Periodic Solutions for Some Second Order Systems with Gyroscopic Forces
MENG Fengjuan
Periodic Solutions for Some Second Order Systems with Gyroscopic Forces
MENG Fengjuan
(School of Mathematics and Physics,Jiangsu University of Technology,Changzhou 213001,Jiangsu)
In this paper,the periodic solutions for second order non-autonomous differential systems with gyroscopic forces are investigated,by applying the least action principle and minimax methods,some existence results of periodic solutions are obtained.
periodic solution;critical point;variational method
1 Introduction
In this paper,we are concerned with the existence of periodic solutions for the following second order system:

where T>0,A is a real antisymmetry constant matrix and F:[0,T]×RN→R satisfies the following assumption:
(H)F(t,x)is measurable in t for each x∈RNand continuously differentiable in x for a.e.t∈[0,T],and there exist a∈C(R+,R+),b∈L1([0,T]; R+)such that

for all x∈RNand a.e.t∈[0,T].
The term A u(t)means that the system has a gyroscopic force(see[1]).For more background,see[2-4]and the references therein.System(1)was mentioned by Ekeland[5]as possible extensions of his basic examples by modern variational methods,but without concrete work.
For the case of A=0,system(1)reduces to the following second order Hamiltonian system

The existence of periodic solutions for(2)was first considered by Berger and Schechter in[6]under the coercive condition.From then on,problem(2)has been extensively studied,many solvability conditions are obtained,such as:the coercivity condition;the convexity conditions;the sublinear nonlinearity conditions;the subquadratic potential conditions;the superquadratic potential conditions;the periodicity conditions and the even type potential condition(See[7-8]and the references therein).
For the case of system(1),in[9-10],the authors have studied the existence of periodic solutions under superquadratic potential conditions and the subconvex condition respectively;in[11-14],Han etc.have investigated the existence of periodic solutions under the sublinear nonlinearity.

where 0≤α<1 and f,g∈L1([0,T];R+).
In this paper,we will consider the case of α=1.Furthermore,we will weak the Ahmad-Lazer-Paul condition

where β is a constant,which has been extensivelyused in the literature.Our main results complete and develop some known results.
2 Preliminaries
We first introduce some notations,inequalities and variational structure of(1),which will be used in our main results.={u:[0,T]→RN|u is absolutely continuous,


with the norm

for all u∈H1T.
one has Sobolev’s inequality

and Wirtinger’s inequality
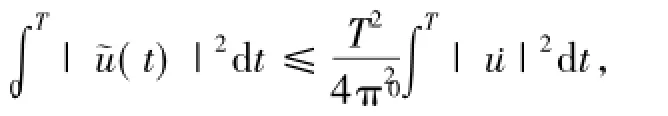
for all u∈H1T(see Proposition 1.3 in[7]),where
Lemma 2.1[11-12]Define the corresponding functional φ onby

It follows from the assumption(H)that φ is continuously differentiable and the solutions of problem(1) corresponding to the critical points of φ.Moreover,one has

3 Main results
For convenience,we denote various positive constants as Ci,i=1,2,….Now we give our main results.
Theorem 3.1 Suppose that F(t,u)satisfies condition(H).Moreover,we have the following assumptions: (i)‖A‖where‖A‖ i s the norm of A as a linear operator from RNto RN;
(ii)there exist f,g∈L1([0,T];R+)withsuch that

f
or all x∈RNand a.e.t∈[0,T];
(iii)

Then problem(1)has at least one solution which minimizes φ on

then a>0.It follows from(ii)and Sobolev’s inequality and Young inequality that

as‖u‖→∞ by(iii)and

By Theorem 1.1 and Corollary 1.1 in[7],the proof is completed.
Remark 3.2 In[12],Han proved the corresponding results when F(t,x)is sublinear growth,i.e.(3)holds.Theorem 3.1 is a complementary and development of this result corresponding to α=1.
Corollary 3.3 Suppose that A=0 and F(t,u) satisfies condition(H)and(ii),(iii)in Theorem 3.1,then problem(2)has at least one solution which minimizes φ on

Remark 3.4 Corollary 3.3 improves Corollary 3 in[15].Instead of(iii),Corollary 3 in[15]requires Ahmad-Lazer-Paul condition

It is easy to see that(iii)in Theorem 3.1 is weaker that(7).
Theorem 3.5 Suppose that F(t,u)satisfies condition(H),and(i)in Theorem 3.1 holds.Moreover,assume F satisfies
(iv)there exist h,k∈L1([0,T];R+)with‖A‖)such that for every ε>0 there exists C(ε)

for all x∈RNand a.e.t∈[0,T];
(v)

where M will be specialized in the proof.Then problem(1)has at least one solution in H1T.
Proof We will accomplish the proof by three steps.
Step 1 First,we prove that φ satisfies the(PS) condition.Assume that{un}is a(PS)sequence for φ,that is{φ(un)}is bounded and φ'(un)→0 as n→∞.In a similar way to(6),we have



for large n.It follows from Wirtinger’s inequality that

for all n,thus we can get

Similar to(6),we can estimate
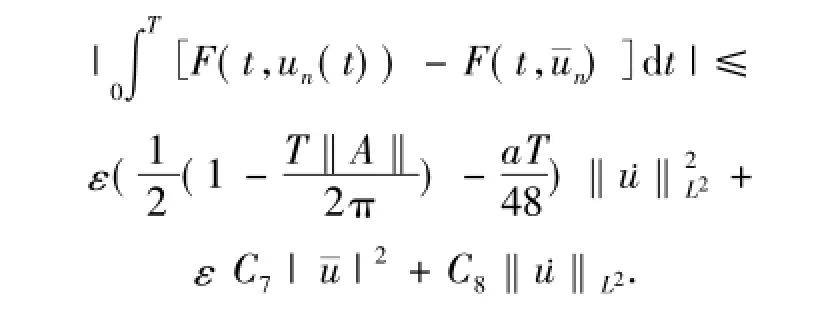
Combining with(8)and Young inequality,we can estimate

It follows from the boundedness of φ(un)and(8) and(9),we have

for all large n.From(v),by choosing ε small enough such that M >C11ε,combining with(10),we can deduce that{珔un}is bounded.Hence{un}is bounded in H1Tby(8).In a way similar to the proof of Proposition 4.1 in[7],see also the proof of Theorem 2.1 in[12],we conclude that the(PS)condition is satisfied.

In fact,similar to(6),we have



Step 3 By(v),we can easily find thatx)dt→+∞ as|x|→∞ for all x∈RN.Hence we can obtain that

Combining with step 1 to 3,by applying the Saddle Point Theorem 4.6 in[16],the proof is completed.
Remark 3.6 In[12],Han proved the corresponding results when F(t,x)is sublinear growth,i.e.(3)holds.Theorem 3.5 is a complementary and development of this result corresponding to α=1.
Corollary 3.7 Suppose that F(t,u)satisfies condition(A)and(iv),(v)in Theorem 3.5,then problem(2)has at least one solution which minimizes φ on
Remark 3.8 Under conditions(3)and(4),in[17],Tang proved the problem(2)has at least one solution in Theorem 1 and Theorem 2.Our Corollary 3.3 and Corollary 3.7 is a complementary and development of Theorem 1 and Theorem 2 in[17]respectively.
[1]ARNOLD V I.Mathematical Methods of Classical Mechanics[M].New York:Springer-Verlag,1978.
[2]MEIROVITCH L.A separation principle for gyroscopic conservative systems[C]//36th Structures,Structural Dynamics and Materials Conference.New Orleans:American Institute of Aeronautics and Astronautics,1997,119:110-119.
[3]SUI Y F,ZHONG W Y.An adjoint symplectic subspace iteration method of gyroscopic dynamic system and the application in rotor dynamic system[C]//ECCOMAS.Jyv skyl ,2004:24-28.
[4]TISSEUR F,MEERBERGEN K.The quadratic eigenvalue problem[J].SIAM Rev,2001,43(2):235-286.
[5]EKELAND I.Convex Methods in Hamiltonian Mechanics[M].Berlin:Springer-Verlag,1990.
[6]BERGER M S,SCHECHTER M.On the solvability of semilinear gradient operator equations[J].Adv Math,1977,25:97-132.
[7]MAWHIN J,WILLEM M.Critical Points Theory and Hamiltonian Systems[M].New York:Springer-Verlag,1989.
[8]TANG C L,WU X P.Some critical point theorems and their applications to periodic solution for second order Hamiltonian systems[J].J Diff Eqns,2010,248(4):660-692.
[9]MENG F J,ZHANG F B.Periodic solutions for some second order systems[J].Nonlinear Anal,2008,68:3388-3396.
[10]MENG F J,ZHANG F B.Existence of periodic solutions for n-dimensional systems of Duffing type[J].Int J Nonlinear Sci,2009,8:162-167.
[11]HAN Z Q.Periodic Solutions for n-dimmensional Duffing Systems(I)[C]//GUO D J.Nonlinear Analysis and its Applications.Beijing:Beijing Sci and Tech Publishing House,1994.
[12]HAN Z Q.Periodic solutions to second order nonautonomous differential systems with unbounded nonlinearities[J].Math Nachr,2011,284(13):1669-1677.
[13]HAN Z Q,WANG S Q,YANG M H.Periodic solutions to second order nonautonomous differential systems with gyroscopic forces[J].Appl Math Lett,2011,24:1343-1346.
[14]HAN Z Q,WANG S Q.Multiple solutions for nonlinear systems with gyroscopic forces[J].Nonlinear Analysis,2012,75: 5756-5764.
[15]ZHAO F K,WU X.Periodic solutions for a class of non-autonomous second order systems[J].J Math Anal Appl,2004,296: 422-434.
[16]RABINOWITW P H.Minimax Methods in Critical Point Theory with Application to Differential Equations[C]//CBMS,65.Providence:Am Math Soc,1986.
[17]TANG C L.Periodic solutions for nonautonomous second order systems with sublinear nonlinearity[J].Proc Am Math Soc,1998,126:3263-3270.
[18]居加敏,王智勇.一類帶阻尼項的次二次二階Hamilton系統的周期解[J].四川師范大學學報(自然科學版),2015,38(3):329-332.
[19]葉一蔚.具有變號位勢的二階Hamilton系統周期解的存在性定理[J].四川師范大學學報(自然科學版),2013,36(3): 337-341.
[20]賀鐵山,陳文革,雷友發.二階離散Hamiltonian系統的多重變號周期解[J].四川師范大學學報(自然科學版),2010,33(4):462-466.
[21]TANG C L,WU X P.Notes on periodic solutions of subquadratic second order systems[J].J Math Anal Appl,2003,285(1): 8-16.
[22]TANG C L,WU X P.Periodic solutions for a class of nonautonomous subquadratic second order Hamiltonian systems[J].J Math Anal Appl,2002,275(2):870-882.
帶gyroscopic項的二階系統周期解的存在性
孟鳳娟
(江蘇理工學院數理學院,江蘇常州213001)
利用臨界點理論中的極小作用原理和極小極大方法,研究了帶有gyroscopic項的二階非自治微分系統周期解的存在性,得到了一些新的可解條件,推廣和改進了已有的結果.
周期解;臨界點;變分方法
O175
A
1001-8395(2016)05-0643-06
2015-07-27
國家自然科學基金(11526100)、江蘇省高校自然科學基金(15KJB110005)和江蘇省青藍工程作者簡介:孟鳳娟(1982—),女,副教授,主要從事非線性泛函分析的研究,E-mail:fjmeng@jsut.edu.cn
10.3969/j.issn.1001-8395.2016.05.005
(編輯 周 俊)
date:2015-07-27
s:This work was supported by NSFC Grant(11401459),Natural Science Fund For Colleges and Universities in Jiangsu Province (15KJB110005)and Qinglan Project of Jiangsu Province
2010 MSC:34C25;58E05;58K05

