一類中立型隨機偏微分方程概周期解的存在性和唯一性

蒲曉琴

一類中立型隨機偏微分方程概周期解的存在性和唯一性

蒲曉琴

(中國民航飛行學院計算機學院，四川廣漢618307)

最近，P．Bezandry和T．Diagana(P．Bezandry，T．Diagana．Appl．Anal．，2007，117:1－10．)引入了均值概周期的概念，研究了一類隨機時滯演化方程，并獲得了其均值概周期存在和唯一的充分條件．我們將應用不動點理論和分數(shù)冪算子方法，獲得一類中立型隨機偏微分方程在均方意義下的概周期解的存在性和唯一性的充分條件．

中立隨機偏微分方程;均值概周期;分數(shù)冪算子;不動點

Bohr最先引了概周期函數(shù)的概念，隨后，Bochner將這概念推廣到Polish空間．近些年來，由于概周期微分方程在物理、化學和生物數(shù)學上的應用，許多學者研究了概周期微分方程概周期解存在性問題［1－17］．隨機微分方程的動力行為也被許多人研究［8－20］．最近，P．Bezandry等［21－22］引入了均值概周期的概念，研究了一類隨機時滯演化方程，并獲得了其均值概周期存在和唯一的充分條件．應用不動點理論和分數(shù)冪算子方法，獲得了一類中立型隨機偏微分方程在均值概周期解的存在性和唯一性的充分條件．

1 基礎知識

假設H和K為實可分的Hilbert空間，它們的范數(shù)分別記為‖·‖和‖·‖K．設(Ω，F(xiàn)，{Ft}t≥0，P)為完備概率空間．L2(K，H)為Hilbert－Schmidt算子，范數(shù)記為‖·‖2．Q為對稱非負算子，Q∈L2(K，H)，并且Q的跡有限．W(t)(t∈R)為定義在(Ω，F(xiàn)，{Ft}t≥0，P)上的取值在K上的Q－Wiener過程［23］．

L2(P，H)為強可測的，均方可積的H值隨機變量的全體，顯然，在范數(shù)‖X‖L2(P，H)=(E‖X‖2)1/2下為Banach空間，其中E為期望．

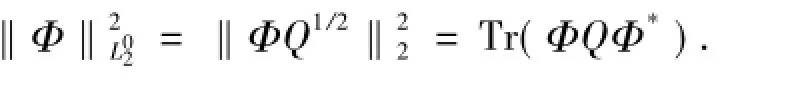
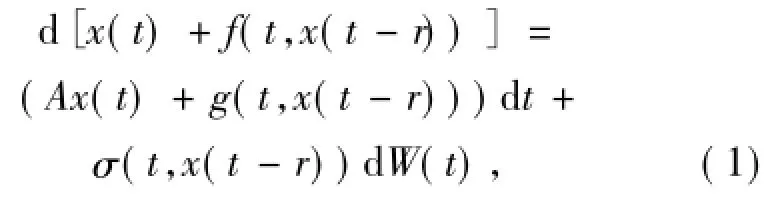
其中，A為Hilbert空間H上的一致指數(shù)穩(wěn)定解析半群最小生成元，r≥0，f，g:R×H→H和σ:R×H→為連續(xù)函數(shù)．

設A:D(A) H→H為定義在Hilbert空間H上的線性算子(T(t))t≥0的解析半群最小生成元，M和δ為正常數(shù)，滿足‖T(t)‖≤Me－δt對任意t≥0．假設0∈ρ(A)，那么，可以定義分數(shù)冪算子Aα對0＜α＜1．它是一閉線性算子，并且定義域D(Aα)在H中稠密．Hα記為Banach空間D(Aα)，其范數(shù)為

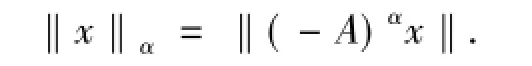
引理1．1［24］下列2個屬性成立:

(i)如果0＜β＜α≤1，那么Hα→Hβ并且當A的預解式為緊時，該嵌入是緊的; (ii)對0＜α≤1，存在Cα以致

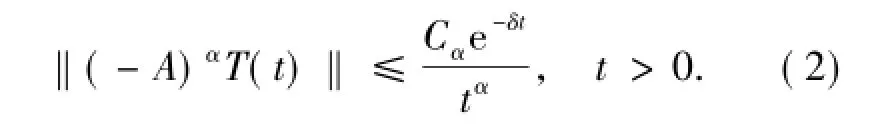
為了獲得主要結果，介紹一些定義和引理．

設(B，‖·‖)為一Banach空間．

定義1．1 一連續(xù)隨機過程X:R→L2(P;B)稱為均值概周期的，如果對每一個ε＞0，存在l(ε)＞0以致任何區(qū)間長度l(ε)最少存在一數(shù)τ滿足

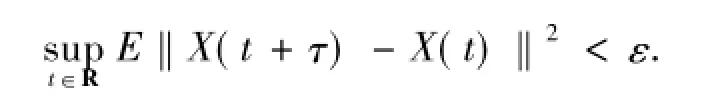
下列為一些均值概周期過程的屬性．

引理1．2［21］如果X屬于AP(R;L2(P;B))，那么:

(i)映射t→E‖X(t)‖2一致連續(xù);

(ii)存在常數(shù)N＞0滿足E‖X(t)‖2≤N，對t∈R．

引理1．3 如果X(·)∈AP(R;L2(P;B))，那么X(·－r)∈AP(R;L2(P;B))，其中r≥0為固定常數(shù)．

證明和文獻［25］中的相似，故省略．

設CUB(R;L2(P;B))為連續(xù)有界隨機過程X: R→L2(P;B)的集合，那么，容易證明在下列范數(shù)下

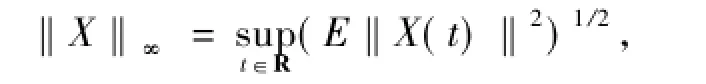
CUB(R;L2(P;B))為Banach空間．

引理1．4［21］AP(R;L2(P;B)) CUB(R; L2(P;B))為閉子空間．

由上可知，AP(R;L2(P;B))在范數(shù)‖·‖∞下是Banach空間．

設(B1，‖·‖B1)和(B2，‖·‖B2)為Banach空間．

定義1．2 稱連續(xù)函數(shù)F:R×B1→B2，(t，Y)→F(t，Y)關于t∈R是均值概周期的，對Y∈K是一致的，其中K B1是緊的，如果對任何ε＞0，存在l(ε，K)＞0以致對任何區(qū)間長度l(ε，K)最少存在一數(shù)τ，對任何隨機過程Y:R→K滿足

引理1．5［21］設F:R×B1→B2，(t，Y)→F(t，Y)關于t∈R是均值概周期的，對Y∈K是一致的，其中K B1是緊的．假設F是以下列方式Lipschitz的

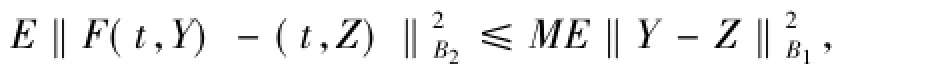
對所有Y，Z∈B1，t∈R成立，其中M＞0，那么對所有均值概周期過程Φ:R→L2(P;B1)，隨機過程t→F(t，Φ(t))是均值概周期的．

(1)式的溫和解的定義如下［26］:

定義1．3 隨機過程x(t):［δ，δ+a)→L2(P; H)，a＞0，稱為(1)式在［δ，δ+a)上的溫和解，如果s→AT(t－s)f(s，x(s－r))在［δ，t)可積，δ＜t＜δ+ a，并且滿足

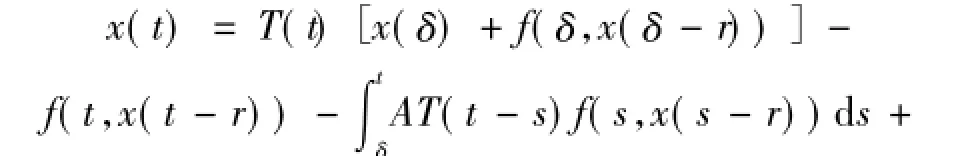
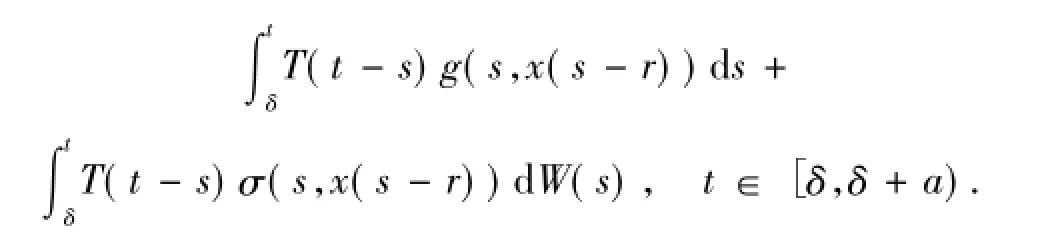
2 主要結果

為了獲得所需結果，假設:

(H1)函數(shù)g(t，x):R×H→H關于t∈R對x∈Ω(Ω H是緊的)是一致均值概周期的．存在α∈(0，1)以致(－A)αf(t，x):R×H→Hα關于t∈R對x∈Ω(Ω H是緊的)是一致均值概周期的．進一步，(－A)αf，g是以下列方式 Lipschitz的:存在 Lf和Lg滿足

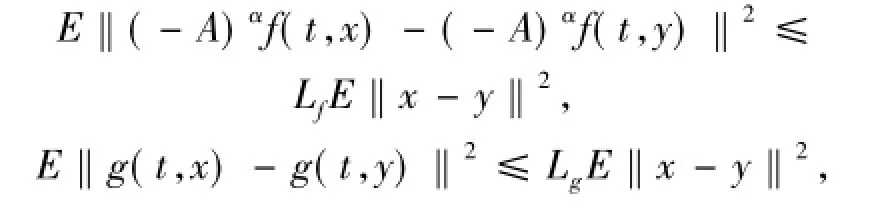
對所有x，y∈H和t∈R成立．

(H2)函數(shù) σ(t，x):R×H→L02關于 t∈R對x∈Ω(Ω H是緊的)是一致均值概周期的．進一步，σ是以下列方式Lipschitz的:存在Lσ滿足

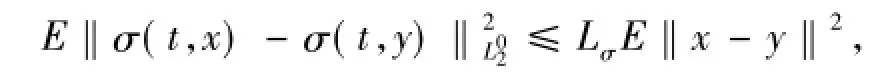
對所有x，y∈H和t∈R成立．

定理2．1 假設(H1)和(H2)成立，并且

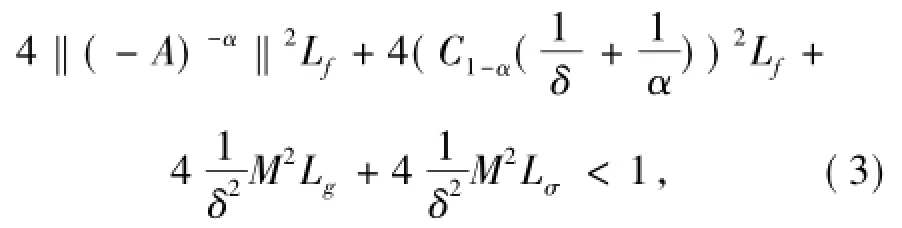
那么(1)式在R上存在唯一均值概周期解．

證明 設Γ:AP(R;L2(P;H))→C(R;L2(P; H))的定義為

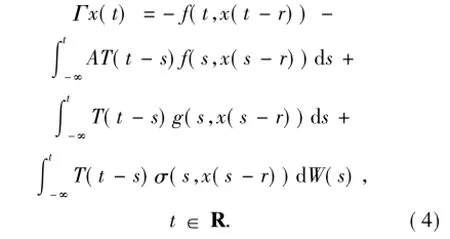
顯然，Γx(·)是連續(xù)的．

定義

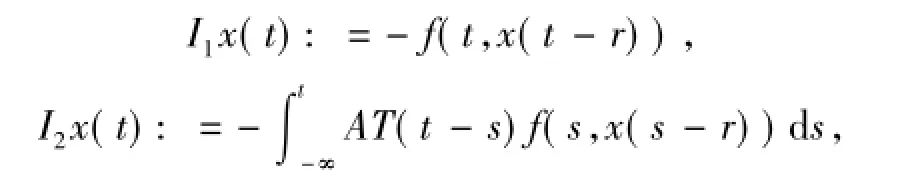
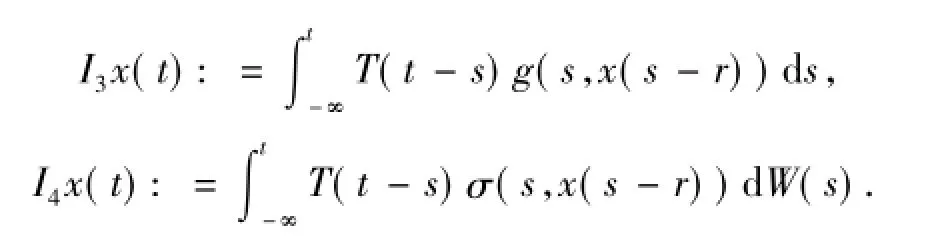
由引理1．3、引理1．5和(H1)可知，當x為均值概周期函數(shù)時，(－A)αf(t，x(t－r))為均值概周期函數(shù)時．由引理1．2，可知(－A)αf(t，x(t－r))有界．由引理1．1和Cauchy－Schwarz不等式可得

由s→AT(t－s)f(s，x(s－r))是可積的在(－∞，t)對任何t∈R，故Γ定義是合適的．

由引理1．3、引理1．5和(H1)可知，當x為均值概周期函數(shù)時，(－A)αf(t，x(t－r))為均值概周期函數(shù)時．因此，對每一個ε＞0存在l(ε)＞0以致對任意區(qū)間長度l(ε)最少存在一個數(shù)τ滿足

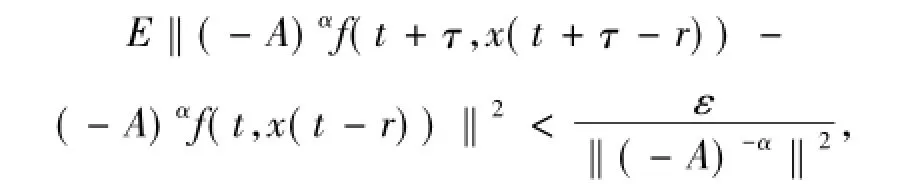
對任何t∈R成立．

同時有

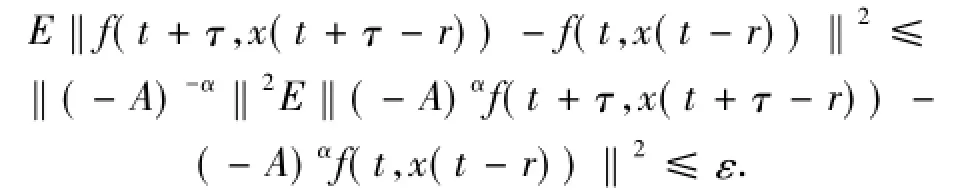
由上可知

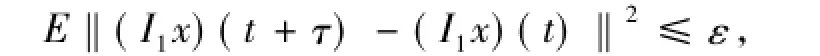
對每個t∈R成立，即I1x(t)均值概周期函數(shù)．

下一步，證明當x是均值概周期函數(shù)I3x(t)和I4x(t)是均值概周期函數(shù)．該證明和文獻［21］中的定理3．2相似，故省略．

下一步證明I2x(t)是均值概周期函數(shù)．由引理1．3、引理1．5和(H1)可得，當x是均值概周期函數(shù)，(－A)αf(t，x(t－r))是均值概周期函數(shù)．因此，對每一個ε＞0存在l(ε)＞0以致對任意區(qū)間長度l(ε)最少存在一個數(shù)τ滿足

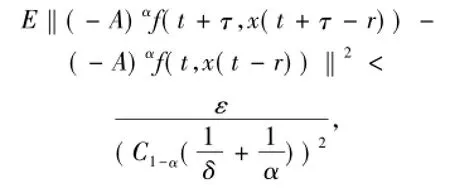
對任何t∈R成立．

由引理1．1可得

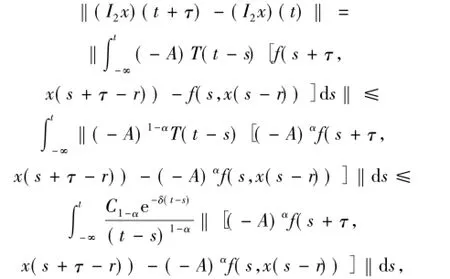
因此，應用Cauchy－Schwarz不等式可得

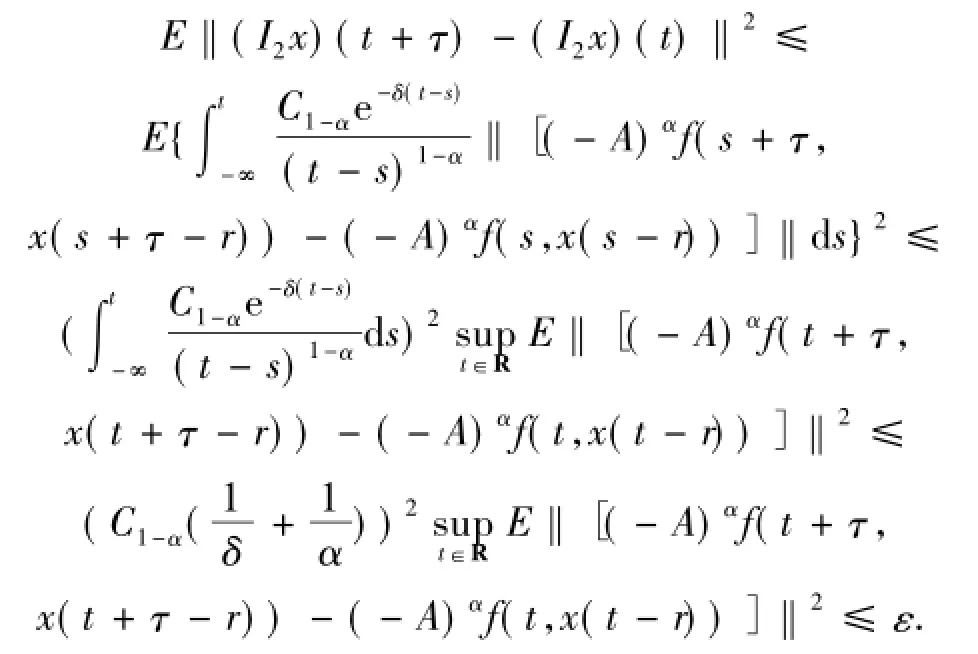
由上可知

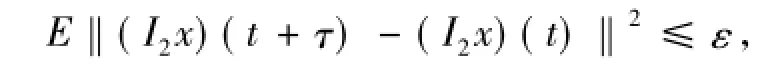
對每個t∈R成立，即I2x(t)是均值概周期函數(shù)．

由上可知，Γ是AP(R;L2(P;H))對自身的映射．下面證明Γ是壓縮映射．

顯然

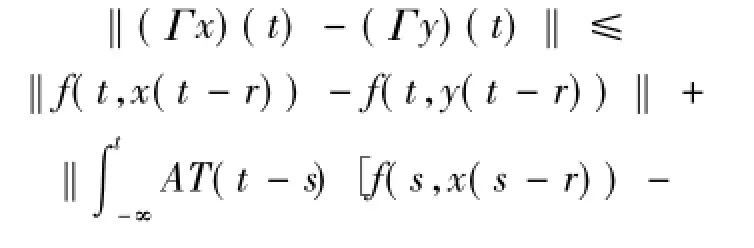
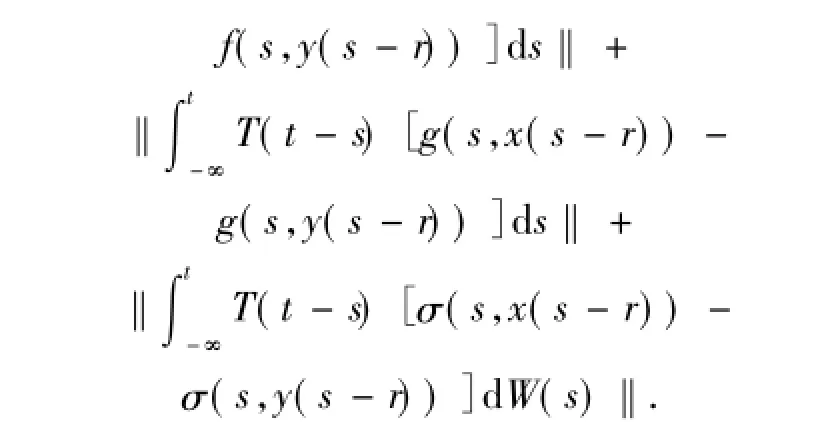
由于

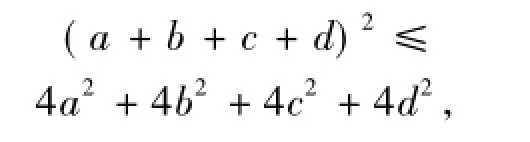
可得

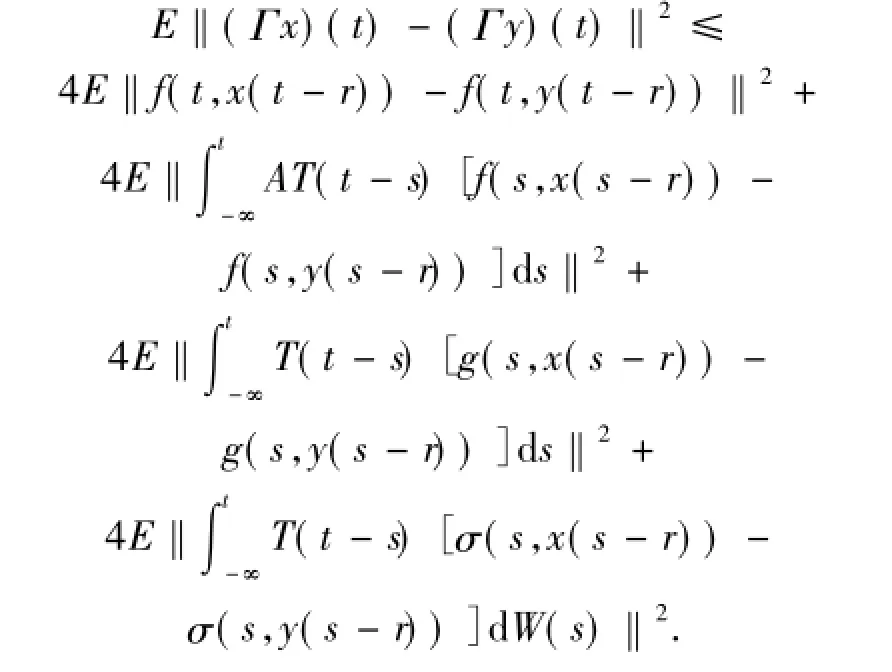
首先，估計上式右邊第一項

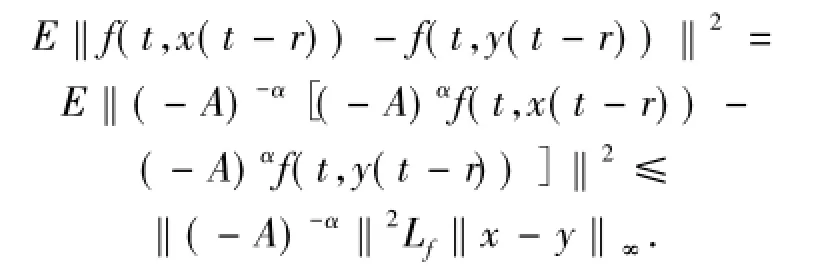
現(xiàn)在估計第二項，由引理1．1、(H1)和Cauchy－Schwarz不等式可得

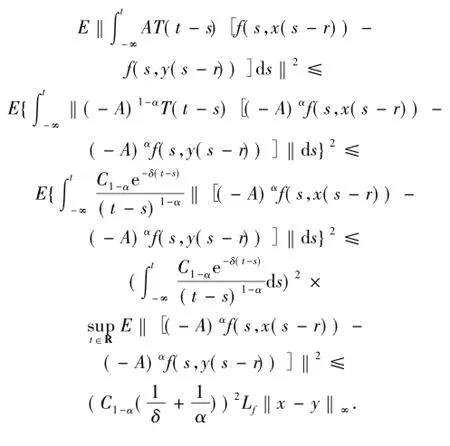
現(xiàn)在估計第三項得

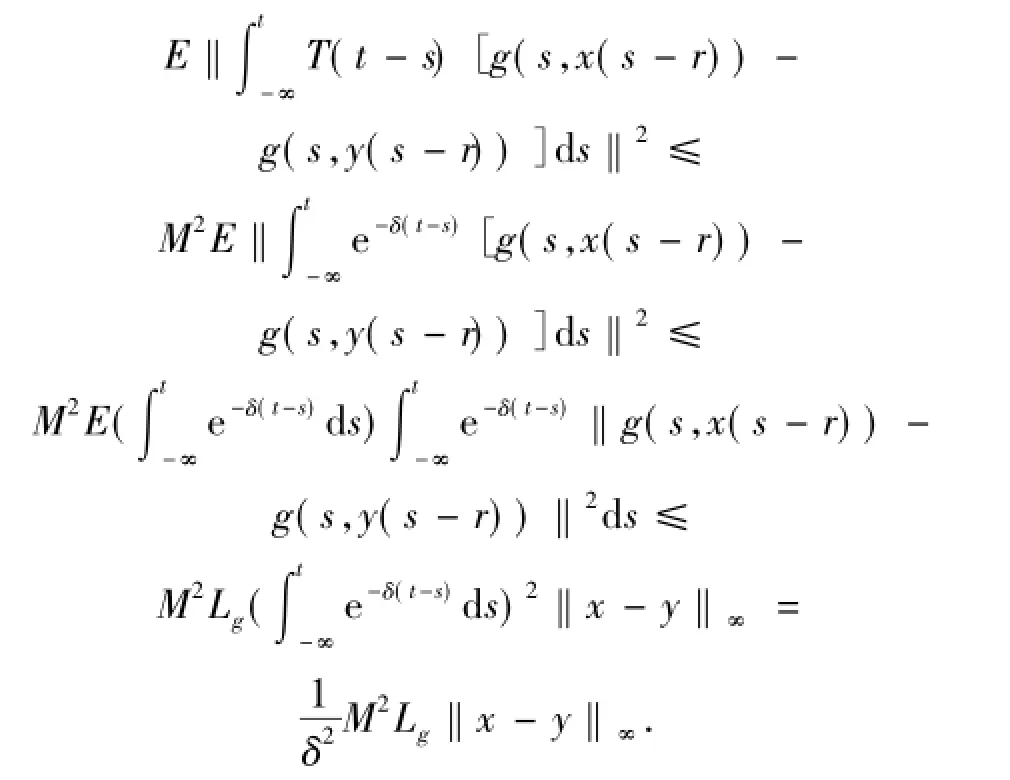
現(xiàn)在估計最后一項，應用建立在文獻［27］中命題1．9的It 積分估計得

因此

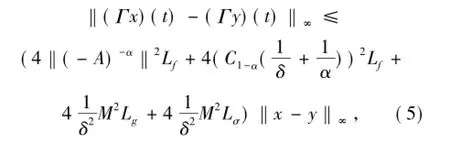
這說明Γ(·)是壓縮的．故Γ(·)存在不動點x∈AP(R;L2(P;H))，即

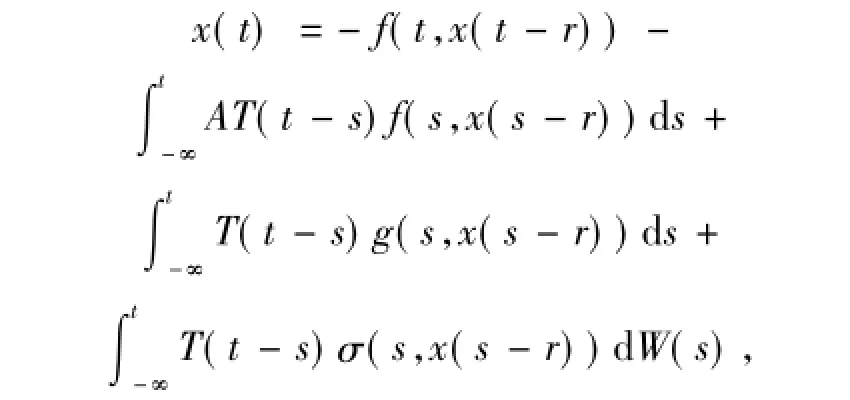
對所有t∈R成立．固定δ∈R可得

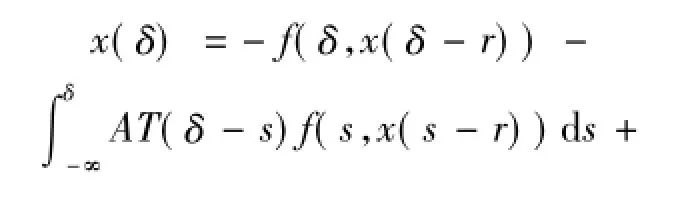
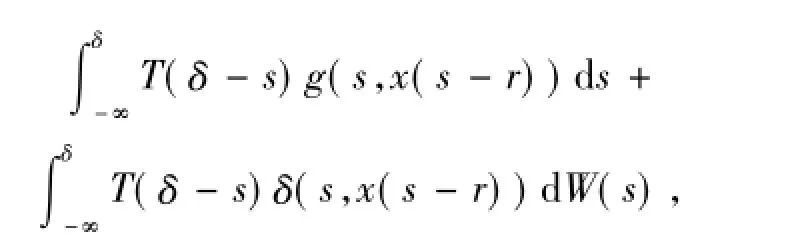
那么

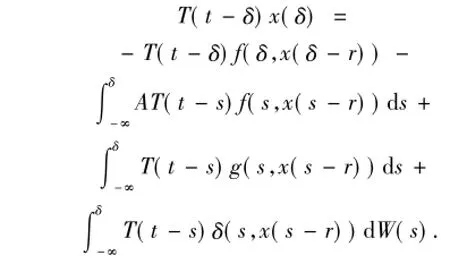
然而，對t≥δ，

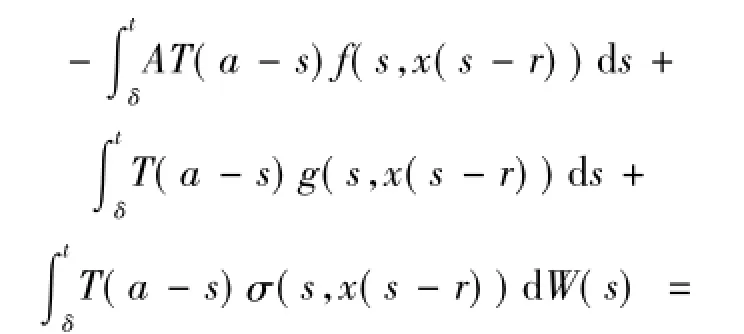
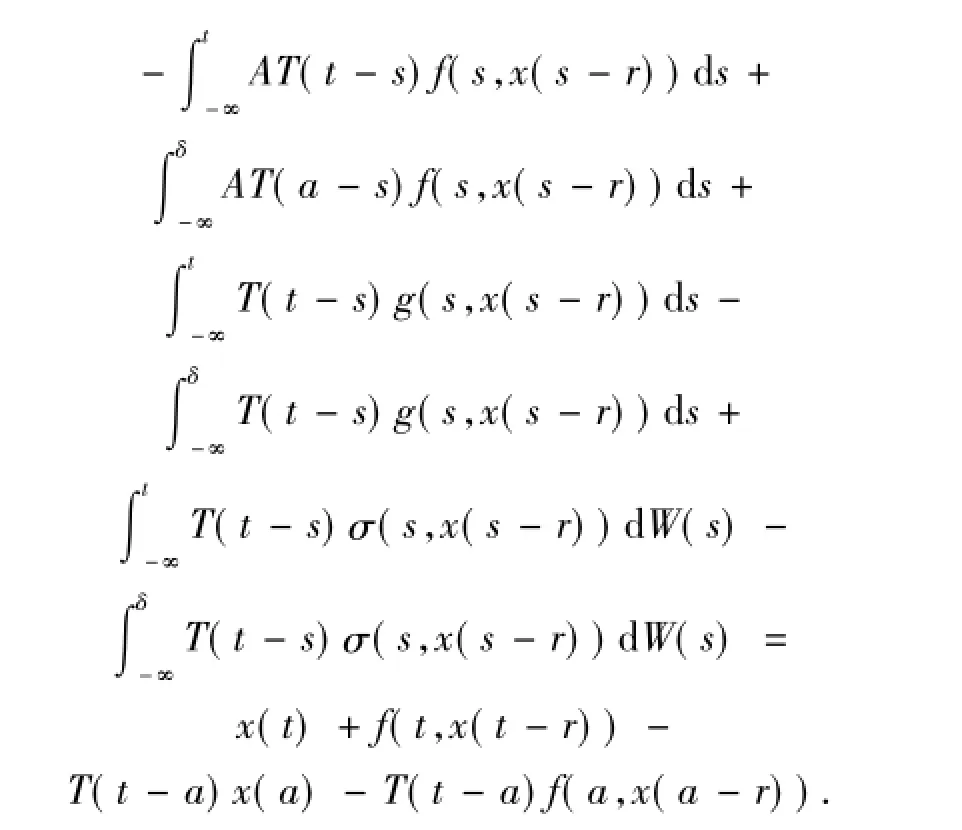
因此，x(t)是(1)式的溫和解．證明完畢．

致謝 中國民航飛行學院面上項目(J2013－39)對本文給予了資助，謹致謝意．

［1］HERN NDEZ E，PELICER M．Asymptotically almost periodic and almost periodic solutions for partial neutral differential equations［J］．Appl Math Lett，2005，18:1265－1272．

［2］HENR QUEZ H，V SQEZ C．Almost periodic solutions of abstract retarded functional－differential equations with unbounded delay［J］．Acta Appl Math，1999，57(2):105－132．

［3］LIU B，TUNC C．Pseudo almost periodic solutions for a class of nonlinear Duffing system with a deviating argument［J］．J Appl Math Comput，2015，49:233－242．

［4］ZHANG L，LI H．Weighted pseudo almost periodic solutions for differential equations with piecewise constant arguments［J］．Bull Aust Math Soc，2015，92:238－250．

［5］AKDAD A，EZZINBI K，SOUDEN L．Pseudo almost periodic and automorphic mild solutions to nonautonomous neutral partial evolution equations［J］．Nonauton Dyn Syst，2015，2:12－30．

［6］SADRATI A，ZERTITI A．Existence and uniqueness of positive almost periodic solutions for systems of nonlinear delay integral equations［J］．Electron J Diff Eqns，2015，116:12．

［7］CAO J，HUANG Z．Existence and exponential stability of weighted pseudo almost periodic classical solutions of integro－differential equations with analytic semigroups［J］．Differ Eqns Dyn Syst，2015，23:241－256．

［8］WANG W T．Positive pseudo almost periodic solutions for a class of differential iterative equations with biological background［J］．Appl Math Lett，2015，46:106－110．

［9］HENRIQUEZ H，CUEVAS C，CAICEDO A．Almost periodic solutions of partial differential equations with delay［J］．Adv Difference Eqns，2015，2015:46－61．

［10］WANG Q，LIU Z，LI Z，et al．Existence and global asymptotic stability of positive almost periodic solutions of a two－species competitive system［J］．Int J Biomath，2014，7:1450040．

［11］ZHUANG R，YUAN R．Weighted pseudo almost periodic solutions of N－th order neutral differential equations with piecewise constant arguments［J］．Acta Math Sin(Engl Ser)，2014，30:1259－1272．

［12］MAQBUL M，BAHUGUANA D．Almost periodic solutions for Stepanov－almost periodic differential equations［J］．Differ Eqns Dyn Syst，2014，22:251－264．

［13］EZZINBI K，ZABSORE I．Pseudo almost periodic solutions of infinite class for some functional differential equations［J］．Appl Anal，2013，92:627－1642．

［14］WANG L，SHI Y．Almost periodic solutions of abstract differential equation with impulse and time delay in Banach space［J］．Int J Appl Math Stat，2013，43:379－386．

［15］VRABEL I．Almost periodic solutions for nonlinear delay evolutions with nonlocal initial conditions［J］．J Evol Eqns，2013，13: 693－714．

［16］DING H，LONG W，N’GU R KATA G．Existence of pseudo almost periodic solutions for a class of partial functional differential equations［J］．Electron J Diff Eqns，2013，104:14．

［17］XU Y．Existence and uniqueness of almost periodic solutions for a class of nonlinear Duffing system with time－varying delays［J］．Electron J Qual Theory Differ Eqns，2012，80:9．

［18］鮑杰，舒級．高階廣義2D Ginzburg－Landau方程的隨機吸引子［J］．四川師范大學學報(自然科學版)，2014，37(3):298－306．

［19］付穎，李揚榮．無界域上帶有可加白噪音的Ginzburg－Landau方程的隨機吸引子［J］．西南大學學報(自然科學版)，2012，37(12):37－42．

［20］杜先云，陳偉．具有可加噪聲的耗散KdV型方程的隨機吸引子［J］．四川師范大學學報(自然科學版)，2012，35(5):651－655．

［21］BEZANDRY P，DIAGANA T．Existence of almost periodic solutions to some stochastic differential equations［J］．Appl Anal，2007，117:1－10．

［22］BEZANDRY P．Existence of almost periodic solutions to some functional integro－differential stochastic evolution equations［J］．Stat Probabil Lett，2008，78:2844－2849．

［23］PRATO G，ZABCZYK J．Stochastic Equations in Infinite Dimensions［M］．Cambridge:Cambridge Univ Press，1992．

［24］PAZY A．Applied Methematical Sciences［M］．New York:Springer－Verlag，1983．

［25］DING H，LIANG J，N’GU R KATA G．Pseudo almost periodicity of some nonautonomous evolution equations with delay［J］．Nonlinear Anal:TMA，2007，67:1412－1418．

［26］LIU K．Stability of Infinite Dimensional Stochastic Differential Equations with Applications［M］．London:Chapman and Hall，2004．

［27］ICHIKAWA A．Stability of semilinear stochastic evolution equations［J］．J Math Anal Appl，1982，90(1):12－44．

Existence and Uniqueness of Almost Periodic Solutions to Some Neutral Stochastic Differential Equations

PU Xiaoqin

(School of Computer Science，Civil Aviation Flight University of China，Ganghan 618307，Sichuan)

P．Bezandry and T．Diagana introduced a new concept of square-mean almost periodicity．They established the existence and uniqueness of square-mean almost periodic mild solutions to some stochastic differential equations and some functional integrodifferential stochastic evolution equations．Sufficient conditions for the existence and uniqueness of a square-mean almost periodic mild solution of a class of abstract neutral stochastic differential equations in a real separable Hilbert space are derived with the help of the Banach fixed point theorem and the fractional power of operators．

neutral stochastic differential equations;square-mean almost periodic;fractional power of operators;fixed point

O175．13

A

1001－8395(2016)05－0659－06

10．3969/j．issn．1001－8395．2016．05．008

(編輯 李德華)

2014－09－01

國家自然科學基金(11326118)

蒲曉琴(1986—)，女，助教，主要從事微分方程定性的研究，E－mail:power1356@163．com

2010 MSC:35B15