一類具p-Laplacian算子的無窮多點邊值問題正解的存在性
王和香,胡衛敏
一類具p-Laplacian算子的無窮多點邊值問題正解的存在性
王和香,胡衛敏*
(伊犁師范學院數學與統計學院,新疆伊寧835000)
利用非線性項在有界集上的高度函數和Kranoselskii不動點定理,研究一類具p-Laplacian算子的無窮多點邊值問題,得到多重正解的存在性,并舉例驗證所得結果的有效性.
分數階邊值問題;p-Laplacian算子;高度函數;Kranoselskii不動點定理
近年來,由于微分方程的廣泛研究,分數階微分方程也在眾多領域受到人們重視.如自動控制、分形和混沌、材料和力學系統、信號處理和系統辨識、神經網絡(ANN)等都涉及到分數階微分方程應用.正是這些應用,極大地促進了分數階微分方程理論及其邊值問題的發展,而越來越多的專著也相繼發表.文獻[1]研究高階非線性多點邊值問題解的存在唯一性;文獻[2]利用Sadovskii不動點定理,討論了Banach空間中的二階常微分方程的一類n點邊值問題;文獻[3]運用Banach壓縮映射原理和廣義Lipschitz條件研究一類m點邊值問題解的存在唯一性;文獻[4]考慮了帶p-Laplacian算子的多點邊值問題正解的存在性.
在文獻[5]中,利用Kranoselskii不動點定理,考慮多點邊值問題
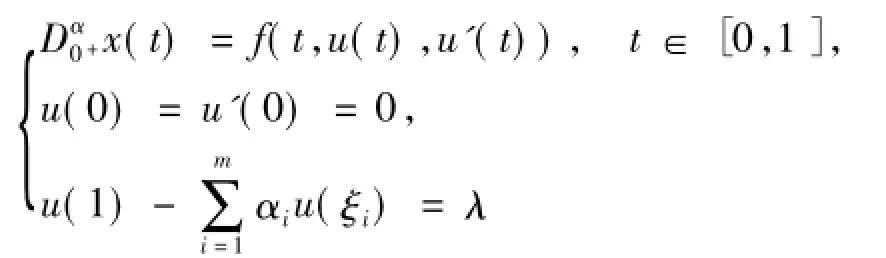
解的存在性,其中,2<α<3,m≥1是整數.
受以上文獻啟發,本文研究一類具p-Laplacian算子的無窮多點邊值問題
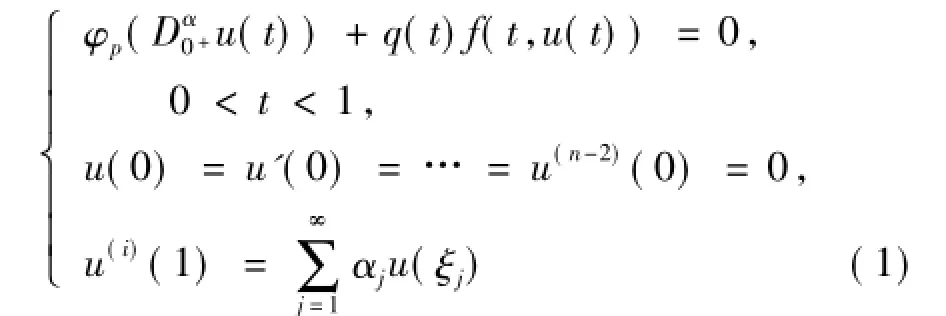
多重正解的存在性,其中φp為p-Laplacian算子,滿足且為標準的Riemann-Liouville導數,α>2,n-1<α≤n,i∈[1,n-2]為一固定的整數,αj≥0,0 < ξ1< ξ2<… < ξj-1<ξj< … <1(j=1,2,i).非線性項f具有奇異性,本文將通過介紹非線性項在有界集上的高度函數,并綜合分析其性質,借助Kranoselskii不動點定理得到邊值問題(1)多重正解的存在性.
1 預備引理
定義1.1[6]函數G(t,s)的α>0階Riemann-Liouville積分是指
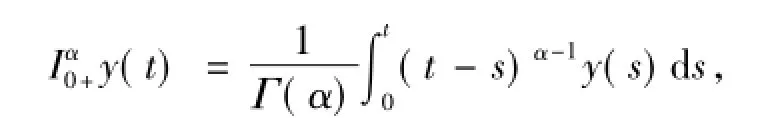
其中,n=[α]+1,右邊是在(0,+∞)上逐點定義.
定義1.2[6]函數G(t,s)的α>0階Riemann-Liouville微分是指
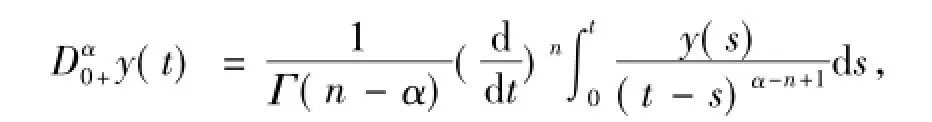
其中,n=[α]+1,右邊是在(0,+∞)上逐點定義.
引理1.1[7]設α >0,如果u∈C(0,1)∩L1(0,1),那么微分方程Dα0+u(t)=0有唯一解
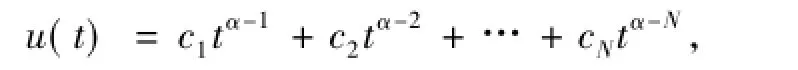
其中ci∈R(i=1,2,…,N),N是大于或等于α的最小整數.
引理1.2[7]設u∈C(0,1)∩ L1(0,1),有其中ci∈R(i=1,2,…,N),N是大于或等于α的最小整數.
引理1.3[8]邊值問題邊值問題
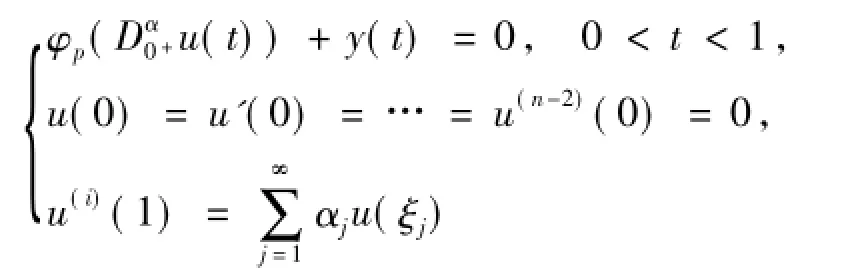
有唯一解
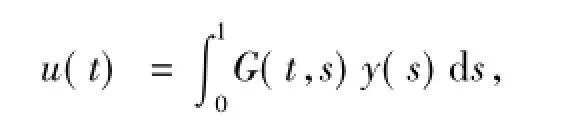
其中
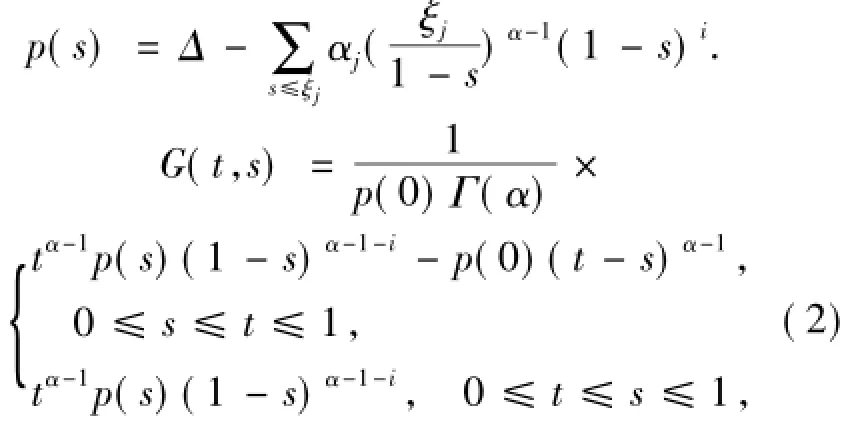
顯然,G(t,s)在[0,1]×[0,1]上連續.引理1.4 邊值問題(1)有唯一解
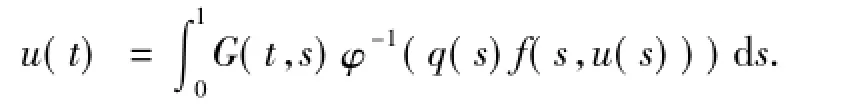
證明 由引理1.3易得證.
引理1.5[8]由(2)式定義的G(t,s)函數有如下性質:
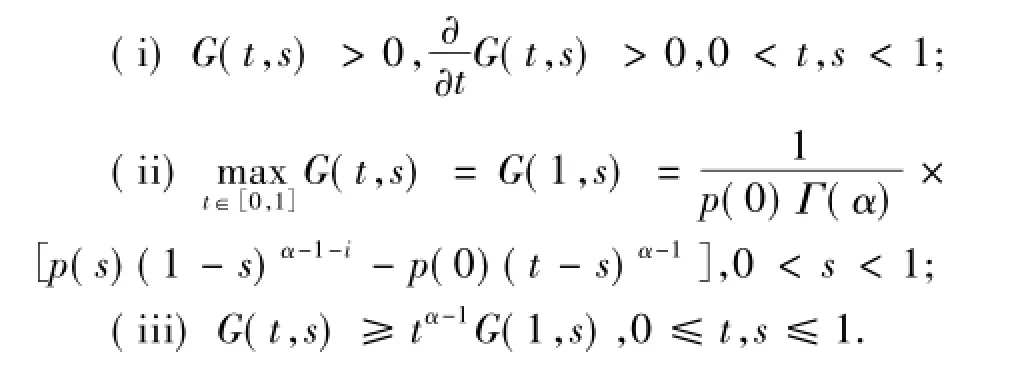
給出以下條件:
(H1)f((0,1)×(0,+∞),[0,+∞))連續;
(H2)q((0,1),[0,+∞))連續且q在(0,1)的任一子區間不恒為零;
(H3)對任意正數r1<r2,存在連續函數γr1,r2: (0,1)→[0,+∞),且當0<t<1時,
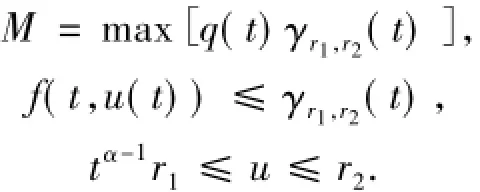
設E=C[0,1]是Banach空間,最大模范數定義為:
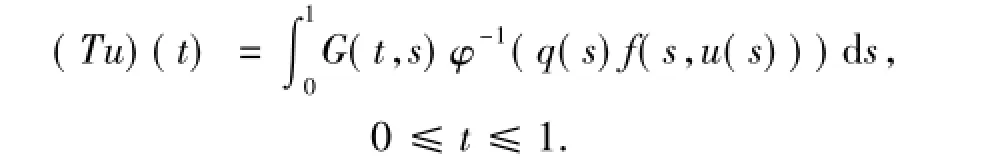
顯然,T:P{0}→C[0,1].
定義錐P為C[0,1]上的非負函數,

定義算子T:
2 主要結論及證明
定理2.1 若條件(H1)~(H3)成立且0<r1<r2,則T:珚Ω(r2)Ω(r1)→P全連續.
聽說文學社曾經愿意給她付印,稿子呈到中央宣傳部書報檢查委員會那里去,擱了半年,結果是不許可。人常常會事后才聰明,回想起來,這正是當然的事;對于生的堅強和死的掙扎,恐怕也確是大背“訓政”之道的。今年五月,只為了《略談皇帝》這一篇文章,這一個氣焰萬丈的委員會就忽然煙消火滅,便是“以身作則”的實地大教訓。
證明 先證T:珚Ω(r2)Ω(r1)→P.對 u∈珚Ω(r2)Ω(r1),由引理1.5,對0≤t≤1有:
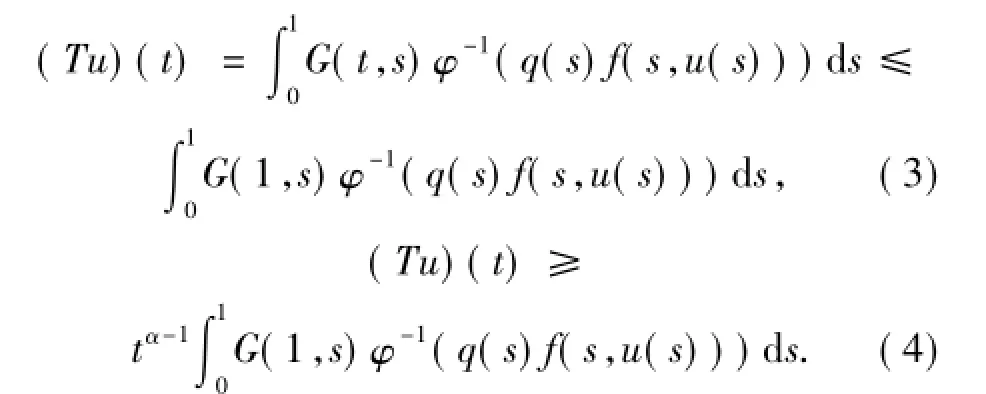
由(3)和(4)式有(Tu)(t)≥ tα-1‖Tu‖,故 T:得證.
注意到
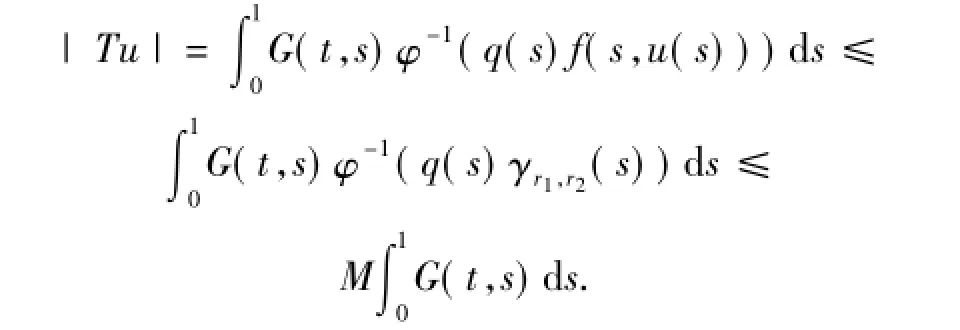
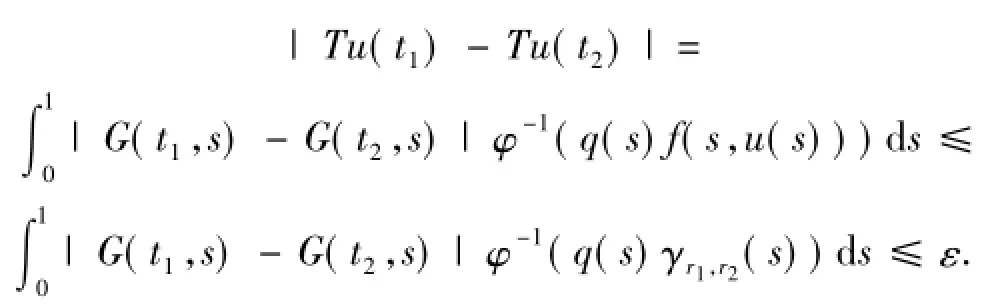
即等度連續,由 Ascoli- Arzela定理得 T:全連續.
下面引入2個高度函數來限制非線性項的范圍:
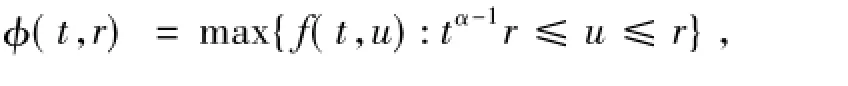

定理2.2 若條件(H1)~(H3)成立且存在2個實數a<b,若:
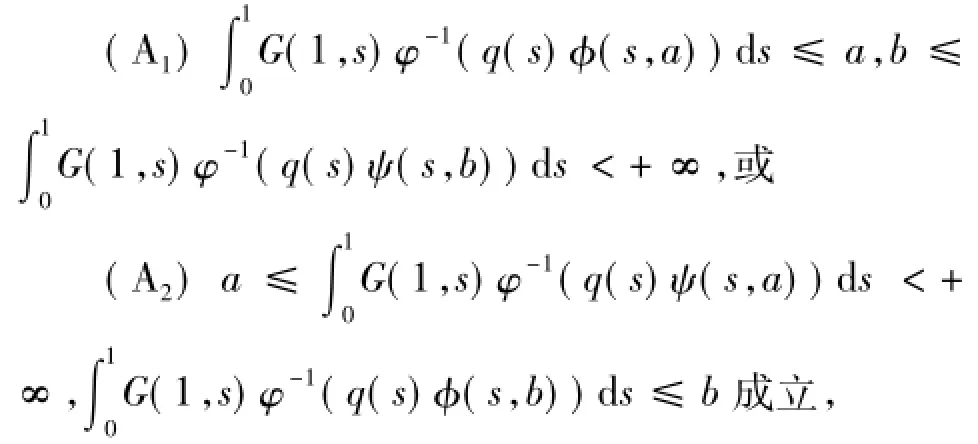
則邊值問題(1)至少有1個嚴格增加的正解u*∈P,且a≤‖u*‖≤b.
設u∈ Ω(a),則‖u‖ =a且
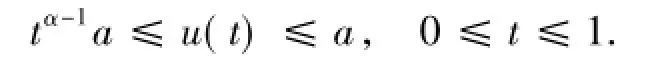
由定義的 (t,a)有
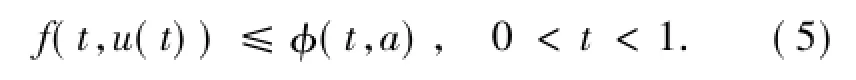
由(5)式和引理1.5有

同理,若u∈ Ω(b),‖u‖ =b且
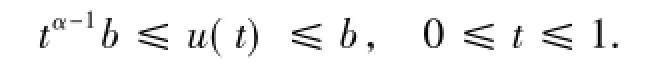
由定義的ψ(t,b)有
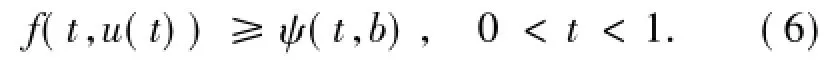
由(6)式和引理1.5有
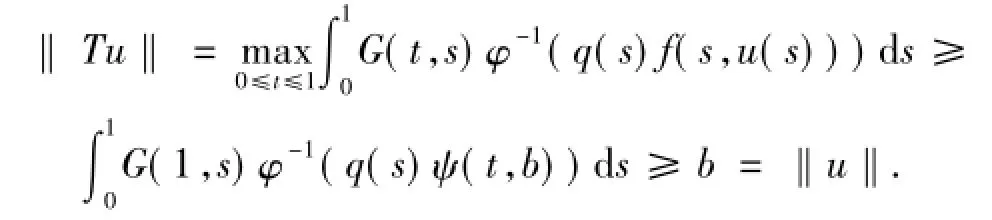
通過Kranoselskii不動點定理,算子T有不動點
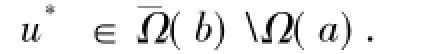
因此

又因為
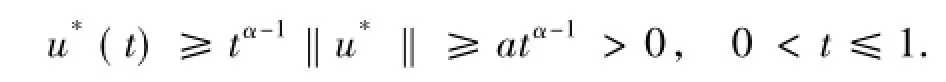
由引理1.5有
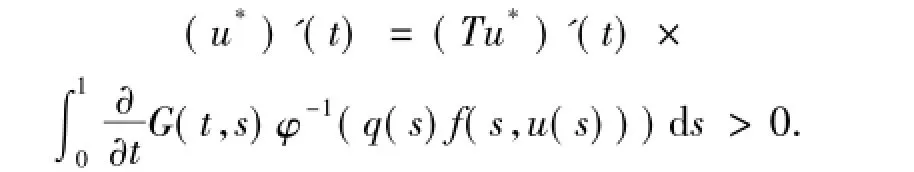
所以u*是一個嚴格增的正解.
定理2.3 若條件(H1)~(H3)成立且存在3
個實數a<b<c,若:

則邊值問題(1)至少有2個嚴格增加的正解u*1,u*2∈P,且
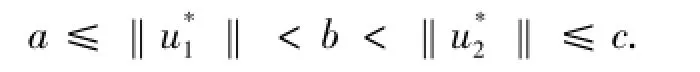
定理2.4 若條件(H1)~(H3)成立且存在m個實數a<b<c<… <m,若:

則邊值問題(1)至少有m-1個嚴格增加的正解:
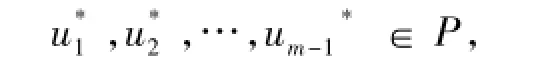
且
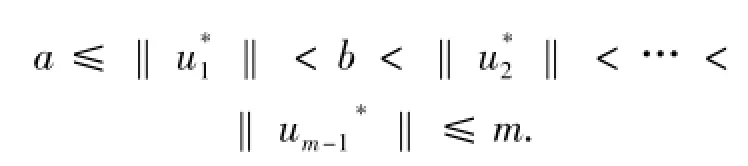
3 舉例
考慮邊值問題

則高度函數 (t,r)、ψ(t,r)滿足:
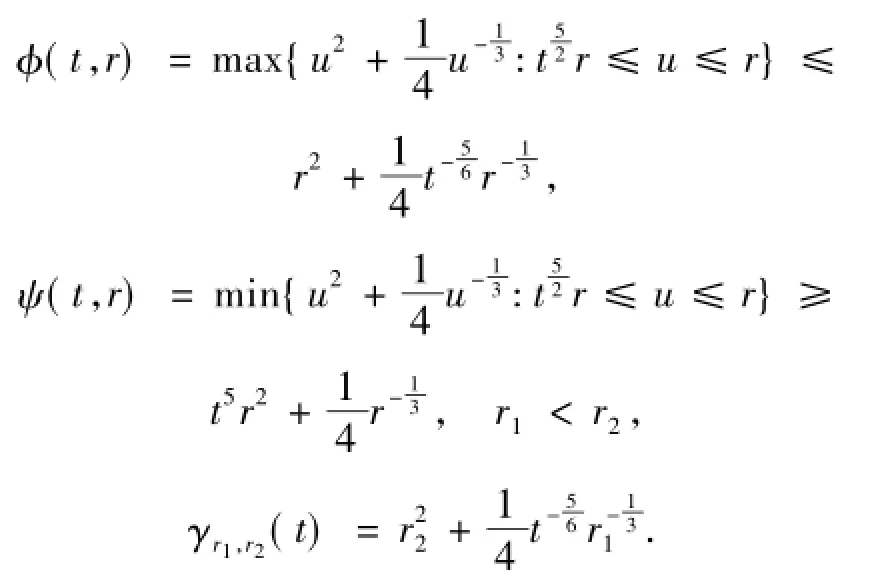
故有:
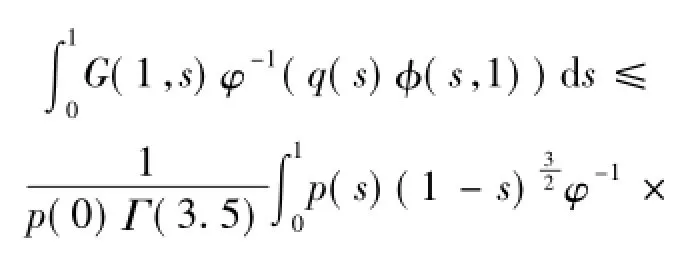
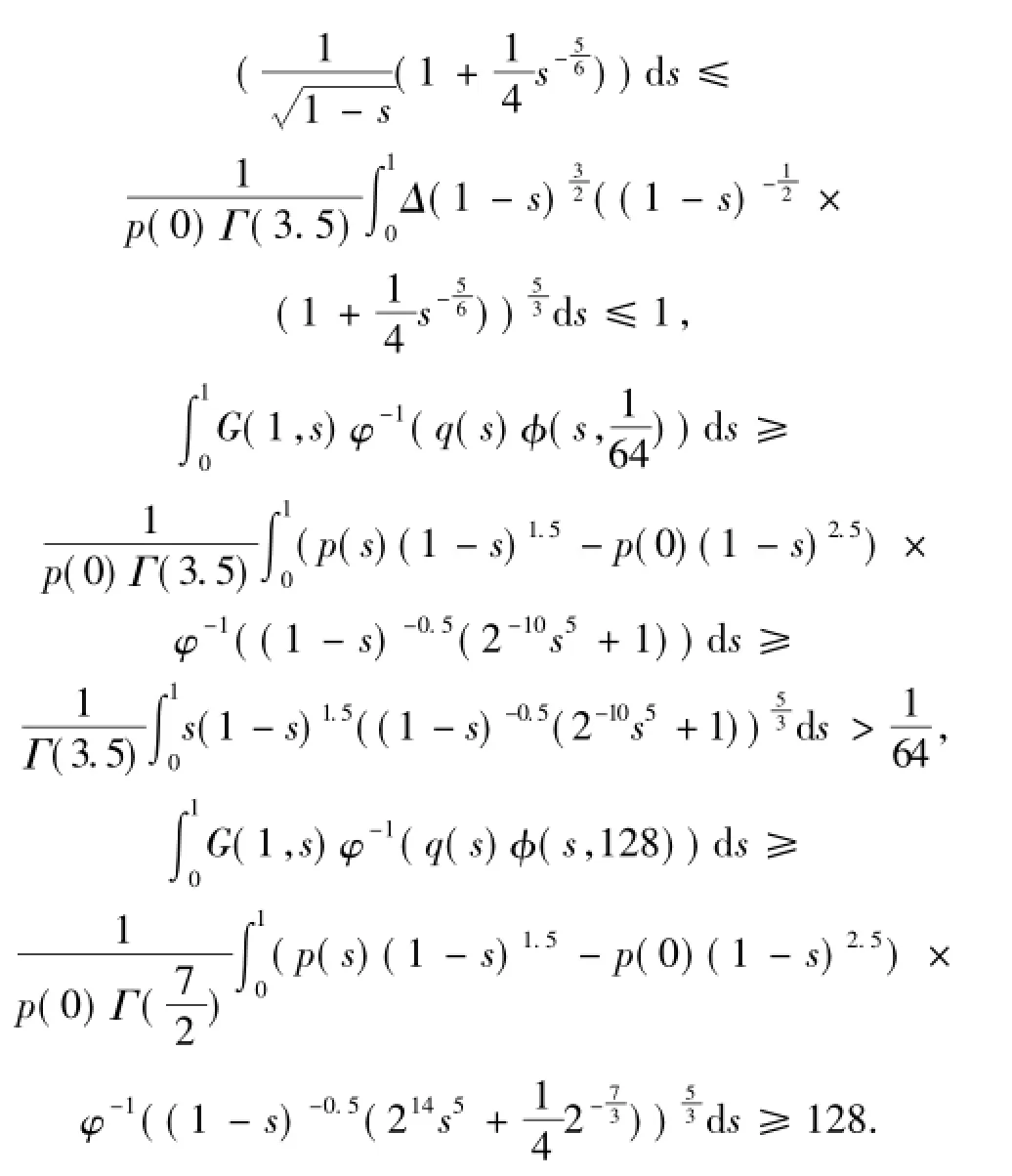
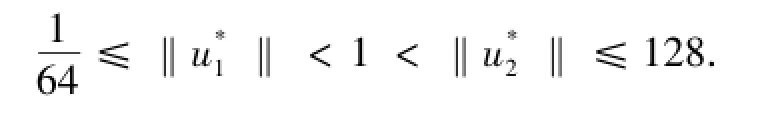
[1]PEI M H,CHANG S K.Existence and uniqueness of solutions for higher order nonlinear multi-point boundary value problems[J].China Quart J Math,2009,24:258-266.
[2]李培巒,張翠,吳玉森.Banach空間中的一類二階n點邊值問題[J].河南科技大學學報(自然科學版),2009,30(4):90-92.
[3]王和香,胡衛敏.非線性分數階微分方程m點邊值問題解的唯一性[J].周口師范學院學報,2015,32(5):30-33.
[4]紀德紅,田玉,葛渭高.帶p-Laplacian算子的多點邊值問題正解的存在性[J].數學學報(中文版),2009,52(1):1-8.
[5]NEMAT N.Existence of solutions for multi point boundary value problems for fractional differential equations[J].Arab J Math Sci,2012,18:165-175.
[6]劉剛,胡衛敏,張穩根.非線性分數階微分方程邊值問題多重正解的存在性[J].云南大學學報(自然科學版),2012,34(3):258-264.
[7]KILBAS A A,SRIVASTAVE H M,TRUJILLO J J.Theory and Applications of Fractional Differential Equations[M].Amsterdam:Elsevier Science,2006.
[8]ZHANG X Q.Positive solutions for a class of singular fractional differential equation with infinite point boundary value conditions[J].Appl Math Lett,2015,39:22-27.
[9]古傳運鄭鳳霞,鐘守銘.一類非線性分數階微分方程邊值問題正解的存在唯一性[J].四川師范大學學報(自然科學版),2015,38(1):72-76.
[10]張愛華,胡衛敏.非線性分數階微分方程邊值問題解的存在性和唯一性[J].東北師大學報(自然科學版),2015,47(4): 36-41.
[11]古傳運,鄭鳳霞,鐘守銘.非線性分數階微分方程邊值問題正解的存在性與唯一性[J].重慶師范大學學報(自然科學版),2015,32(1):96-101.
[12]ZHANG X Q,WANG L,SUN Q.Existence of positive solutions for nonlinear fractional differential equations with integralboundary conditions and a parameter[J].Appl Math Comput,2014,226:708-718.
[13]HAN Z L,LU H L,ZHANG C.Positive solutions for eigenvalue problems of fractional differential equation with generalized p-Laplacian[J].Appl Math Comput,2015,257:526-536.
[14]高婷,韓曉玲.一類奇異三階m點邊值問題正解的存在性[J].四川師范大學學報(自然科學版),2015,38(5):648-655.
[15]MA D X.Positive solutions of multi-point boundary value problem of fractional differential equation[J].Arab J Math Sci,2015,21:225-236.
[16]CHAI G Q.Positive solutions for boundary value problem of fractional differential equation with p-Laplacian operator[J].Boundary Value Problems,2012,2012:18-38.
[17]白婧.一類三階非線性微分方程的奇周期解[J].四川大學學報(自然科學版),2015,52(6):1217-1220.
Existence of Solutions for a Class of Infinite Point Boundary Value Problem with p-Laplacian Operators
WANG Hexiang,HU Weimin
(College of Mathematics and Statistics,Yili Normal University,Yining 835000,Xinjiang)
Taking advantage of nonlinear term’s height function on bound set and Kranoselskii fixed point theorem,we research one class of infinite point boundary value problem with p-laplacian operator,obtain the existence of multiplicity of positive solutions and examine the efficiency of the results via examples.
fractional boundary value problem;p-Laplacian operator;height function;Kranoselskii fixed point theorem
O175.8
A
1001-8395(2016)05-0691-05
10.3969/j.issn.1001-8395.2016.05.014
(編輯 余 毅)
2015-12-06
新疆維吾爾自治區高校科研計劃重點項目(XJEDU2014I040)和新疆維吾爾自治區自然科學基金(201318101-14)
*通信作者簡介:胡衛敏(1968—),男,教授,主要從事微分方程理論與應用的研究,E-mail:hwm680702@163.com
2010 MSC:34A08

