有限體積元法定價歐式期權

甘小艇，易華

有限體積元法定價歐式期權

甘小艇1，2，易華3*

(1.楚雄師范學院數學與統計學院，云南楚雄675000;2.同濟大學數學系，上海200092; 3.井岡山大學數理學院，江西吉安343000)

基于線性有限元空間，構造歐式期權定價模型的2種穩定的全離散有限體積元格式.數值實驗結果表明，有限體積元法的定價是高效的，而Crank－Nicolson格式的數值效果要優于隱式歐拉格式.

有限體積元法;歐式期權;Crank－Nicolson;隱式歐拉

有限體積元法由R.H.Li等［1］最早提出，目前已和有限差分法、有限元法成為當今重要的三大偏微分方程(PDE)數值方法之一.該方法格式構造簡單、數值精度高、網格剖分靈活和易于處理復雜的邊界條件，更重要的是可以保持某些物理量局部守恒性，因此在計算流體力學等領域有著十分廣泛的應用［2－4］.

近年來，有限體積元法也被眾多學者應用于期權定價問題的計算中，并受到了廣泛的關注和研究［5－13］，其中，文獻［5－9］采用的是一種被稱之為“Fitted Finite Volume Method”的離散方法對期權定價模型進行離散，最后得到期權的價格.文獻［10］則對“stochastic volatility”模型的對流項和擴散項分別采用有限體積法和有限元法離散，并結合懲罰函數法得到期權的價格.由于“Fitted”有限體積法并非基于有限元空間下的離散，因此該方法并不是真正意義上的有限體積元法，它更像是積分插值的改進.最新的經典有限體積法定價美式期權和求解復雜發展方程詳見文獻［12－15］.

通常地，歐式期權具有顯示的定價公式，但過于復雜的表達式往往給計算帶來許多困難，因此有時候人們更愿意采用先進而穩定的數值方法結合計算機技術進行科學計算.基于此，本文獨立于文獻［6］的思想，詳細討論了一類更加簡單直接定價歐式期權的有限體積元格式，數值實驗驗證了該方法的穩定性和高效性.

1 歐式期權模型

本文考慮的歐式期權定價問題是定義在無限的區域［0，∞)×［0，T］上，并帶有Dirichlet邊界條件和一個終止條件.為了利用有限體積元法求解這些問題，把問題限制在一個截斷的區域［0，X］×［0，T］，其中X要取得足夠大，一般為原生資產價格的3倍或者更多［12－13，16］.

考慮歐式期權的初邊值問題，求u=u(x，t)使得

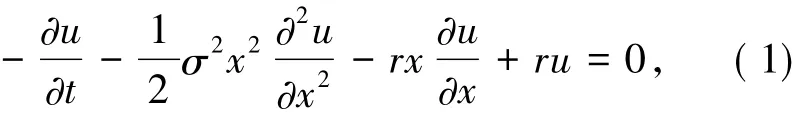
其中，函數u是期權價格，它隨著原生資產價格x和時間t的變化而變化，σ和r分別為波動率和無風險利率(均假定為常數)，

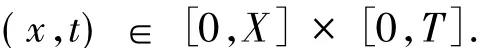
對于歐式看跌期權，邊界條件是

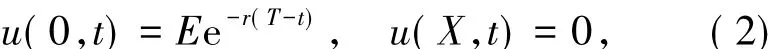
終止條件u(x，T)=g(x)，收益函數

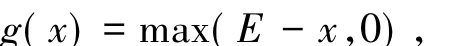
E為敲定價格.

另外，對于歐式看漲情況.邊界條件是

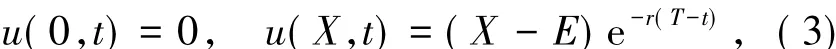
終止條件u(x，T)=g(x)，收益函數

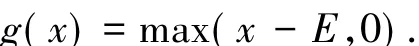
2 有限體積元離散

本節主要給出歐式看跌期權的有限體積元離散，看漲情況的處理相類似.

文中記Hm(I)為通常的Sobolev空間，‖·‖m為相應的范數，H0(I)=L2(I)空間上的范數與內積分別記為‖·‖和(·，·).設X是一個Banach空間，u(t):［0，T］→X表示X值函數，并定義空間如下

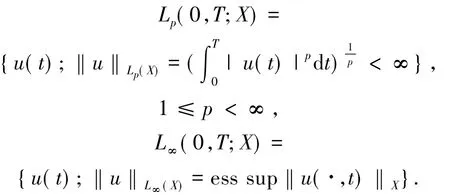
為敘述方便，在Black－Scholes偏微分方程(1)中令τ=T－t(文中仍記時間變量為t)，然后將其簡化為如下變系數拋物型方程

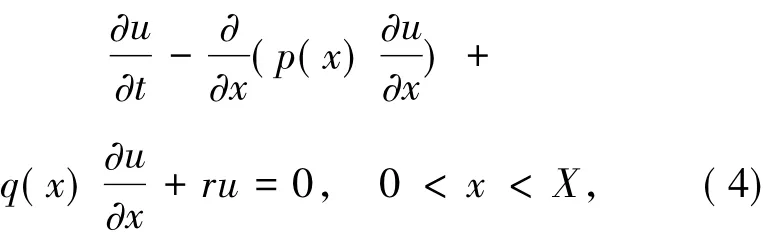
其中，系數

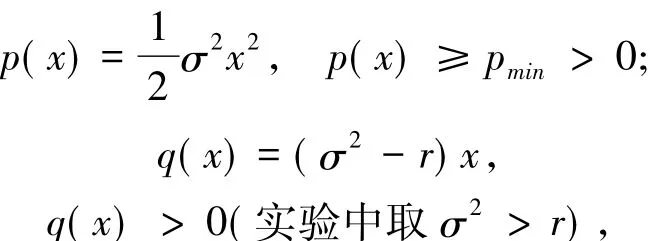
σ和r可看成常數，相應的終止條件轉變為初值問題(以看跌為例)，即

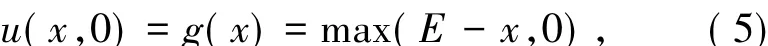
邊界條件仍為(2)式.采用類似文獻［12］中的試探函數空間Uh(線性元)和檢驗函數空間Vh(分片常數)，則求解拋物型方程(4)的半離散有限體積元格式為:求uh∈Uh使得

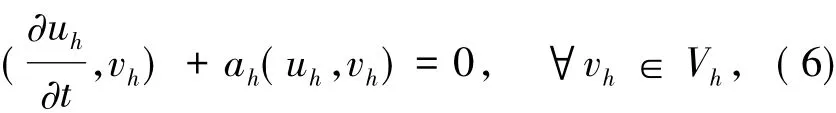
或者等價

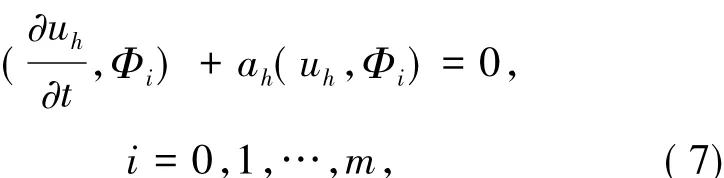
其中Φi為Vh的特稱函數，雙線性形式

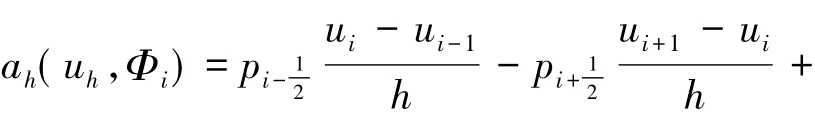
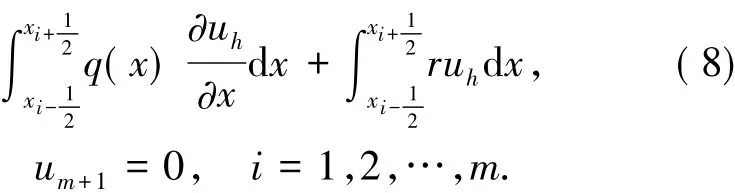
經有限體積元離散，則半離散有限體積元格式(7)對應的矩陣形式為

其中

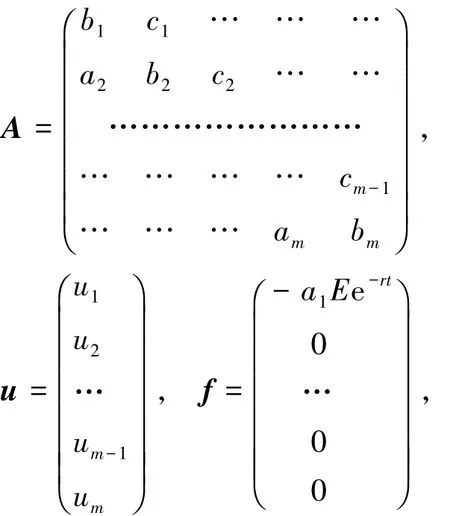
其中，A為m階方陣，u為m×1列向量，矩陣A中的元素詳見文獻［10］.

下面考慮方程(4)的全離散有限體積元格式.假設時間方向上步長為Δt=T/n，則［0，T］對應如下均勻網格剖分

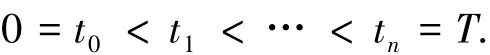
采用相同的Uh和Vh，則方程(4)的全離散有限體積格式為:求(j=1，2，…，n)∈Uh使得

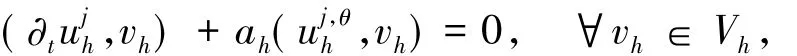
或者等價

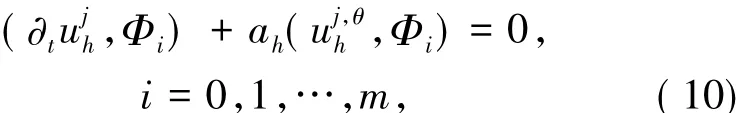
其中

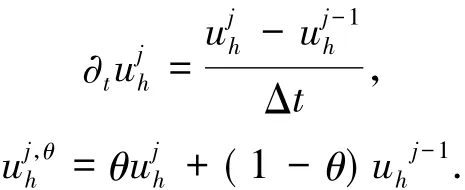
當θ=1時，格式為隱式歐拉格式;當θ=1/2時，格式變為Crank－Nicolson格式.由(9)式可知，(10)式對應的矩陣形式為

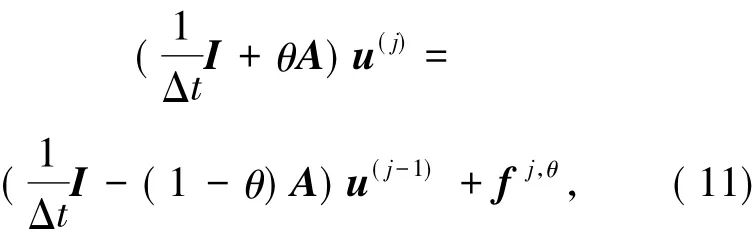
其中

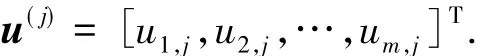
在(11)式中令

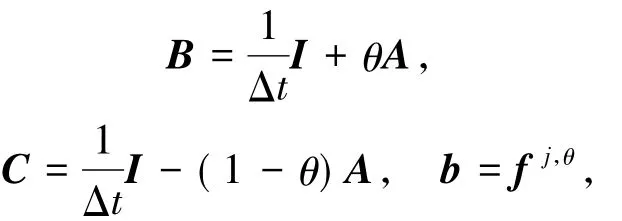
則全離散格式對應的矩陣形式為

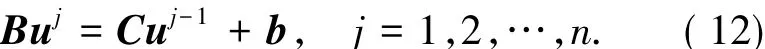
關于代數系統(12)的計算將在下面給予詳細討論.

3 數值實驗

本節的數值實驗以2個歐式期權為例，詳細驗證了本文中有限體積元格式的有效性.所有的代數方程組均采用超松弛迭代法(SOR)求解，其中松弛因子取經驗值ω=1.2，容許誤差為ρtol=1e－8.

數值實驗中的IT指的是所有時間層上的平均迭代步數，CPU表示SOR方法計算所有時間層所需的CPU時間，誤差指的是相對誤差，計算公式如下:

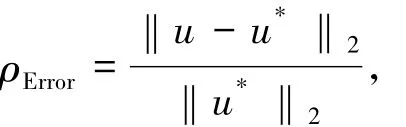
其中，‖·‖2表示向量的2范數，u和u*分別表示t=0時刻時的數值解和精確解(精確解可采用BS定價公式計算).

例1模型(1)中參數

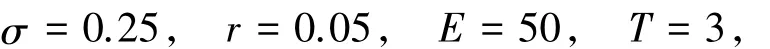
數值計算區域取:［0，150］×［0，3］，其中模型參數與文獻［16］取值相同.

首先，在圖1中顯示了當網格剖分(m，n)= (599，600)時，采用Crank－Nicolson有限體積元格式計算歐式看跌和看漲期權所得的價格曲面(當t =0時).

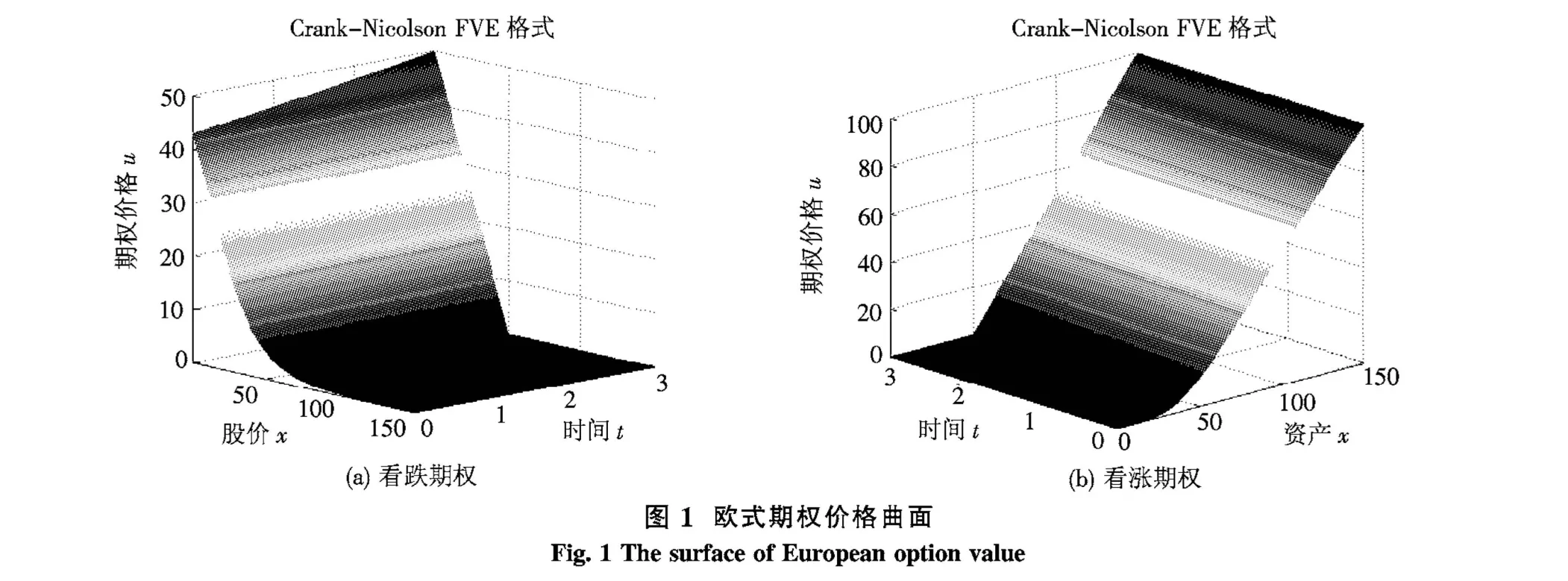
表1 有限體積元解與真解比較Table 1Comparison of finite volume element solutions and true solutions

表1中給出了數值解與精確解的比較.由表1可看出，2種全離散格式的計算都是精確的，且數值精度都隨著網格剖分數的增大變得更加精確，而Crank－Nicolson格式的數值效果要好于隱式歐拉格式.

表2比較2種全離散格式的平均迭代步數，CPU時間和誤差.由表2可知，2種全離散格式所需的CPU時間都隨著網格的加密而變大.當空間剖分數不變，時間方向翻倍時，2種格式的迭代步數變小，這是因為矩陣

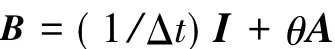
隨著時間剖分數變小而變得更加對角占優的緣故.然而，相同的網格剖分下，Crank－Nicolson格式所需的迭代步數和CPU時間都要比隱式歐拉的少，這說明了Crank－Nicolson格式的計算效率要優于隱式歐拉格式.

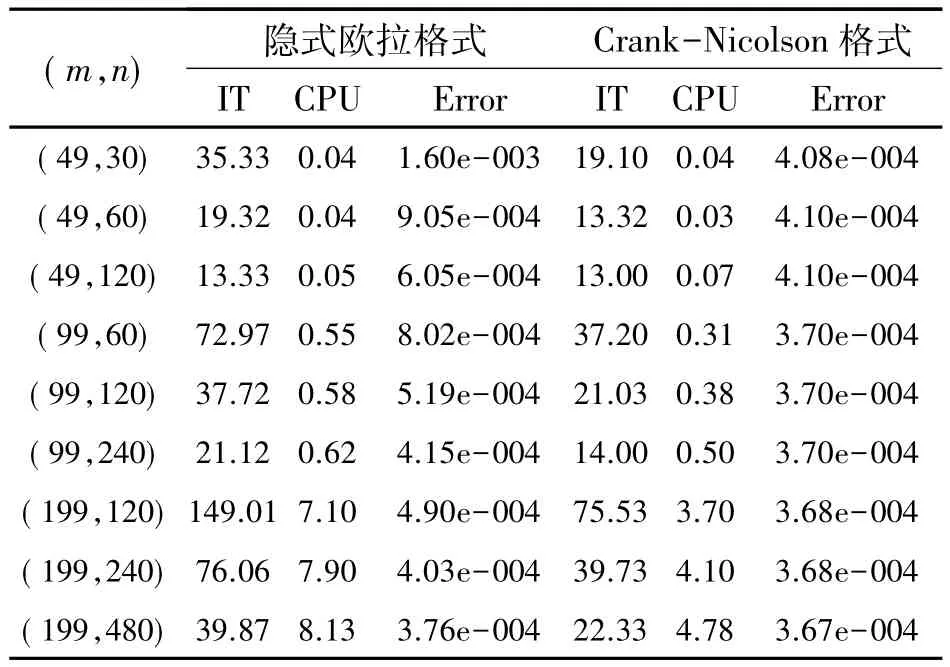
表2 2種格式平均迭代步數，所需的CPU時間和誤差比較Table 2Comparison of two schemes on average iteration number，CPU time and error

例2考慮帶支付紅利(股息)的歐式看漲期權

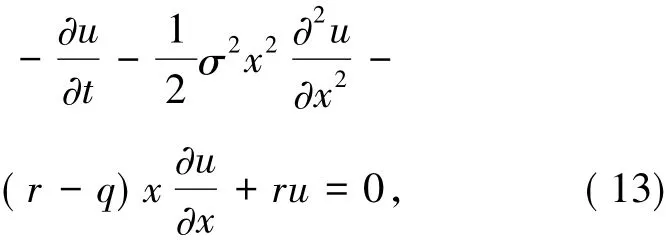
其中，q為紅利率，相應的邊界條件

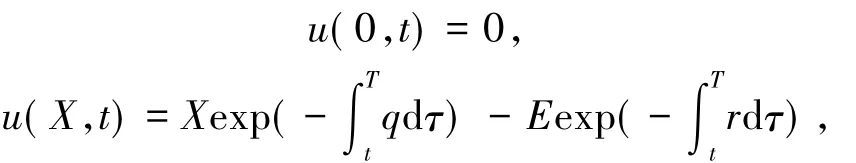
終止條件

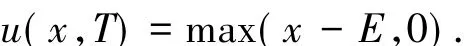
模型(13)中參數取

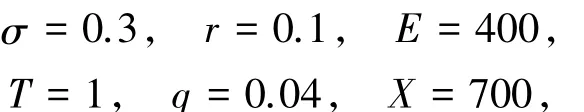
數值計算區域取:［0，700］×［0，1］，這里的模型參數與文獻［6］取值相同.

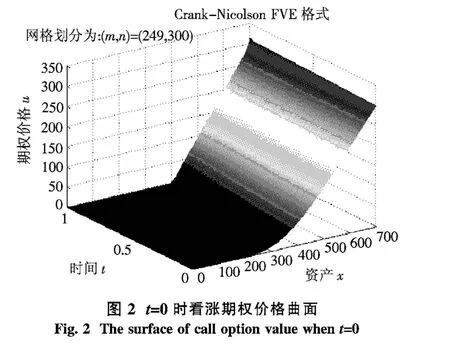
圖2中顯示了當網格剖分(m，n)=(349，300)時，采用Crank－Nicolson有限體積元格式計算所得的價格曲面(當t=0時).由圖2可知，文中格式計算所得的期權價格曲面與文獻［6］非常吻合.值得注意的是，基于簡化的變系數拋物型方程的離散，文中所構造的有限體積元格式要比文獻［6］更加簡單直接，更有利于進一步應用和推廣.

4 結語

本文考慮了歐式期權定價模型的2種穩定的全離散有限體積元格式，超松弛(SOR)迭代法被用來求解離散后的代數系統.2個數值例子結果表明，文中所構造的有限體積元格式在期權定價中是有效的，Crank－Nicolson格式的數值效果要優于隱式歐拉格式.由于線性有限體積元法的檢驗函數空間取為分片常數函數空間，其計算量明顯少于有限元法，并具有著較高的數值精度，數值實驗也驗證了這一點，因此該方法在期權定價中具有著非常廣泛的應用前景.

致謝井岡山大學博士啟動基金(JZB1304)對本文給予了資助，謹致謝意.

［1］LI R H，CHEN Z Y，WU W.Generalized Difference Methods for Differential Equations:Numerical Analysis of Finite Volume Methods［M］.New York:Marcel Dekker，2000.

［2］費斯泰赫.計算流體動力學導論:有限體積法［M］.2版.北京:世界圖書出版公司，2010.

［3］甘小艇，陽鶯，張坤.四邊形網上雙曲型方程的有限體積元法［J］.四川師范大學學報(自然科學版)，2012，35(5):618－624.

［4］甘小艇，張坤.拋物和雙曲方程的全離散間斷有限體積元法［J］.西北師范大學學報(自然科學版)，2012，48(1):15－21.

［5］HUANG C S，HUANG C H，WANG S.A fitted finite volume method for the valuation of options on assets with stochastic volatilities［J］.Comput，2006，77(3):297－320.

［6］WANG S.A novel fitted finite volume method for the Black－Scholes equation governing option pricing［J］.Numer Analysis，2004，24(4):699－720.

［7］ANGERMANN L，WANG S.Convergence of a fitted finite volume method for the penalized Black－Scholes equation governing European and American option pricing［J］.Numer Math，2007，106(1):1－40.

［8］WANG S，YANG X Q，TEO K L.Power enaplty method for a linear complementarity problem arising from American option valuation［J］.J Optim Theor Appl，2006，129(2):227－254.

［9］ZHANG K，WANG S.Pricing options under jump diffusion processes with fitted finite volume method［J］.Appl Math Comput，2008，201(1):398－413.

［10］ZVAN R，FORSYTH P A，VETZAL K R.Penalty methods for American options with stochastic volatility［J］.J Comput Appl Math，1998，91(2):199－218.

［11］FORSYTH P A，VETZAL K R.Quadratic convergence for valuing American options using a penalty method［J］.SIAM J SCI Comput，2002，23(6):2095－2122.

［12］甘小艇，殷俊鋒.有限體積法定價美式期權［J］.應用數學與計算數學學報，2014，28(3):253－265.

［13］甘小艇，殷俊鋒.二次有限體積法定價美式期權［J］.計算數學，2015，37(1):67－82.

［14］GAN X T，YIN J F.Symmetric finite volume method for second order variable coefficient hyperbolic equations［J］.Appl Math Comput，2015，258(19):1015－1028.

［15］GAN X T，YIN J F.Symmetric finite volume element approximations of second order linear hyperbolic integro－differential equations［J］.Comput Math Appl，2015，70(10):2589－2600.

［16］ACHDOU Y，PIRONNEAU O.Computational methods for option pricing［M］.Philadelphia:Society for Industrial and Applied Mathematics，2005.

Finite Volume Element Method for Pricing European Option

GAN Xiaoting1，2，YI Hua3
(1.College of Mathematics and Statistics，Chuxiong Normal College，Chuxiong 675000，Yunnan; 2.Department of Mathematics，Tongji University，Shanghai 200092; 3.School of Mathematics and Physics，Jinggangshan University，Ji’an 343009，Jiangxi)

In this paper，we drive two kinds of full discrete finite volume element schemes for pricing European option based on a linear finite element space.Numerical experiments confirm the perform of the finite volume element method，and further show that the Crank-Nicolson scheme is more efficient than the backward Euler scheme.

finite volume element method;european option;Crank-Nicolson;backward Euler

O241.82

A

1001－8395(2016)03－0327－05

10.3969/j.issn.1001－8395.2016.03.005

(編輯陶志寧)

2015－03－11

云南省青年項目(2013FD045)和云南省教育廳科研項目(2015Y443)

*通信作者簡介:易華(1973—)，男，講師，主要從事數值計算的研究，E－mail:yihua@whu.edu.cn

2010 MSC:65M08