利用圖形旋轉變換解題的思路探索
張建能
摘 要:這一輪課程改革,對幾何作了較大幅度的調整,印象較深之一是加強了“幾何變換”的內容,即從變換的角度去認識傳統幾何中的證題術。初中幾何涉及的變換主要有平移、對稱和旋轉,本文從“旋轉”這一角度舉些例子,供大家參考。
關鍵詞:數學;旋轉;解題
中圖分類號:G632 文獻標識碼:B 文章編號:1002-7661(2016)11-319-01
例1、如圖〔1〕分別以正方形ABCD的邊AB、AD為直徑畫半圓,若正方形的邊長為 ,求陰影部分的面積。
解:連AC、BD如右圖,則繞AD中點將圖中②逆時針旋轉 到圖中③,將圖中①繞AB中點順時針方向旋轉 到圖中④,則原圖中陰影部分的面積就和△DBC的面積相等,所以圖中陰影部分的面積=S⊿DCB = S 正方形ABCD= 。這里我們用旋轉變換的方法改變了圖中①和②的位置,從而順利地完成了計算。
例2、如圖⑵所示,在⊿ABC中,AB=AC,∠BAC= ,D是BC上任一點,試說明 。
證法一(非旋轉法):過A點作
AE⊥BC于E,如圖⑶,則容易證明AE=BE=EC,又BD=BE-DE,DC=CE+DE,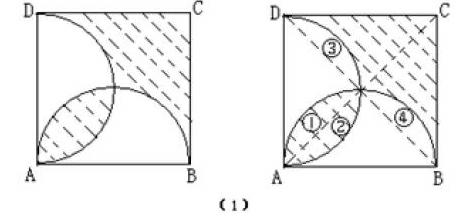
所以 , ,所以 = + = ,而在直角三角形ADE中,存在 ,所以 ,這是傳統的證明方法。
本題考慮到BD、DC、AD三線段分散在兩個三角形中,而且構成平方和的條件不明顯,若利用旋轉變換,將BD、DC放到一個三角形中,若這個三角形是直角三角形,則創造 就更能接近所證的目標了。
證法二(旋轉法): 將△ADC繞A點順時針方向旋轉 到△AEB,如圖⑷, 連DE, 易知△ADE、△DBE均為直角三角形,且AE=AD,BE=DC, 所以在Rt△EBD中有 ,在Rt△AED中有 ,所以
例3、如圖⑸所示,P為正方形內一點,且PA=1,BP=2,PC=3,求∠APB的大小
解: 如圖(6),將⊿BPC繞B點逆時針旋轉 到△BEA, 連EP易知∠PBE= 且AE=PC=3 BE=BP=2,在Rt⊿BEP中, , 且∠EPB= ,在⊿AEP中 ,又 ,所以△APE是直角三角形,即∠APE= ,∠APB=∠APE+∠EPB= + = ,即∠APB為
傳統幾何中,有許多旋轉的例子,尤其是正方形和等腰三角形中。如圖(7),正方形ABCD的邊長為1,AB、AD上各有一點P、Q,如果△APQ的周長為2,求∠PCQ的度數。
將△CDQ繞C點逆時針旋轉90°像圖(8)那樣,立刻可得QA+AB+BE=2,由△APQ周長為2得 PQ=PE,進一步可得△CPQ≌△CPE,∠PCQ=∠PCE,又∠QCE=90°,所以∠PCQ=45°
又如圖(9),△ABC中,AB=AC,P為三角形內一點,且∠APB>∠APC,求證:PC>PB。將△APB繞A點逆時針旋轉成右圖那樣,不難得到條件∠APB>∠APC變成了∠PQC>∠QPC,從而PC>CQ,由旋轉關系,PC>PB。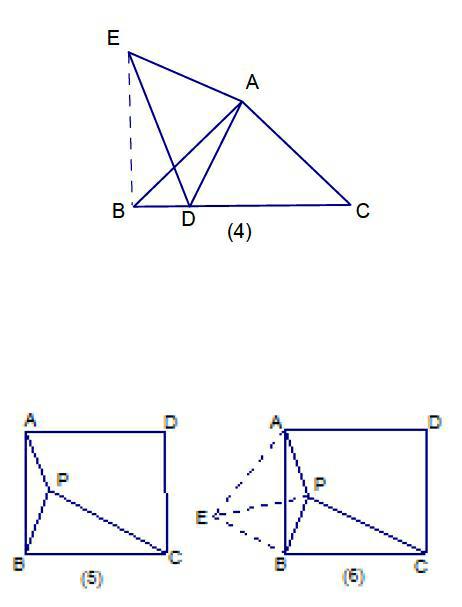
最能體現旋轉法的莫過于下面這個問題了:如圖(10),四邊形ABCD中,AB=AD,∠A=∠C=90°,其面積為16,求A到BC的距離。通過旋轉變換,將圖(10)變成圖(11),答案可以脫口而出:距離為4!類似的例子可以舉出許多,這里不再贅述。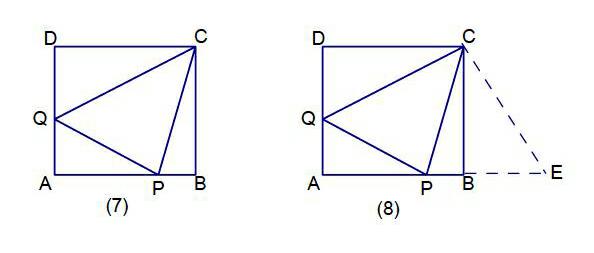
綜上可見,正確利用圖形的旋轉變換可大大提高解題效率,不過在使用這一方法解題時還需注意圖形旋轉變換的基礎,即存在相等的線段,故這種方法一般常用于等腰三角形,正方形圖形中。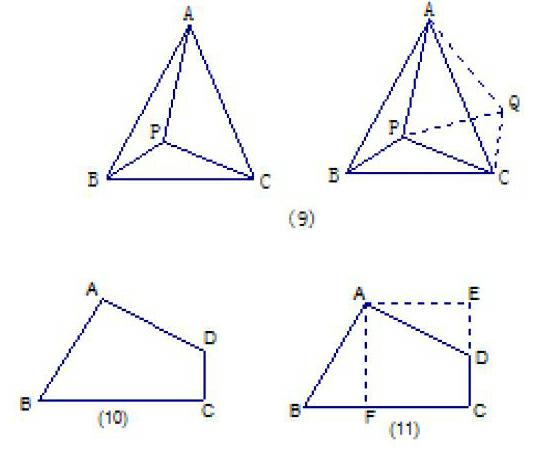
參考文獻:
[1] 吳秀明.加強基本圖形研究,有效實施初中數學圖形歸納[J].數理化學習:初中版,2015(3).
[2] 桑高峰.淺析初中數學圖形類問題教學[J].中學時代,2014(16)

