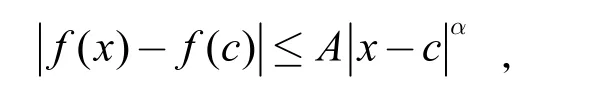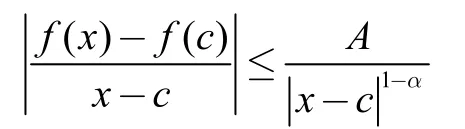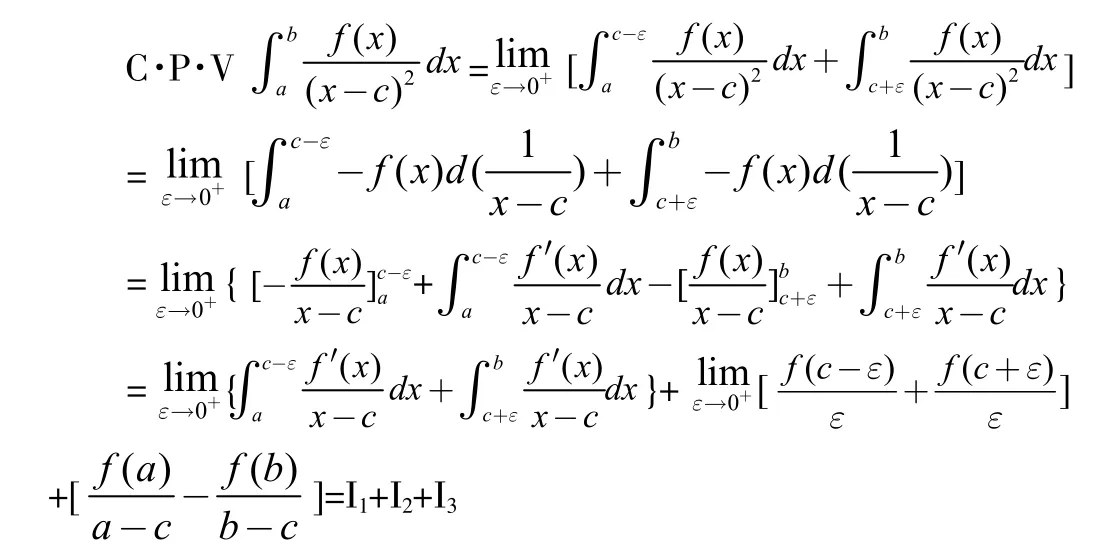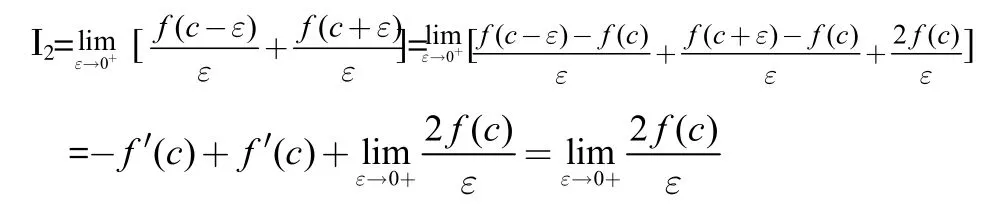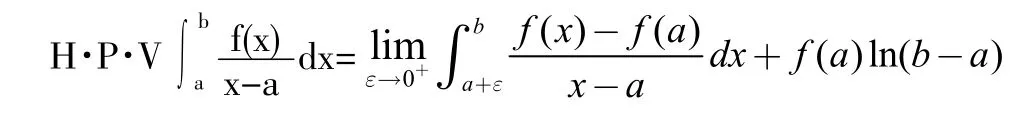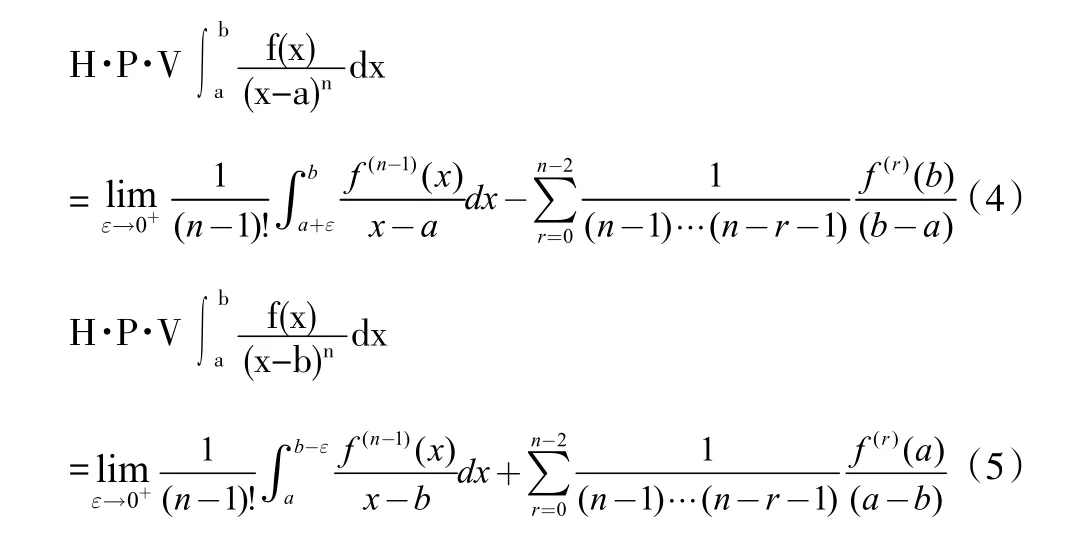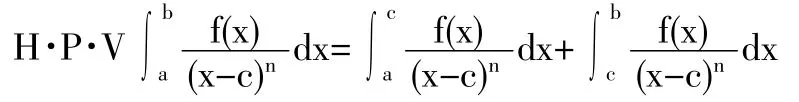存在奇點的一維高階奇異積分

孫蘭香（滄州師范學院數學與統計學院，河北滄州061001）

?

存在奇點的一維高階奇異積分

孫蘭香
（滄州師范學院數學與統計學院，河北滄州061001）

摘要：文章研究實數域中奇異積分的主值問題。這是基于數學分析中對廣義積分的研究作的進一步深入探討的工作。文中定義了一維奇異積分的Cauchy主值與Hadamard主值并給出了相應的公式。

關鍵詞：高階奇異積分；Cauchy主值；Hadamard主值

Keywords:higher order singular integral；Cauchy principle value；Hadamard principle value

在復分析中有對復平面上奇異積分的主值研究，在實數域中也存在積分問題的研究，對收斂的廣義積分可以求得其積分值，而發散的廣義積分不存在積分值。這里便出現了值得探討的新問題，即研究發散的廣義積分的主值問題。

定義1設f（x）定義于（a，b）上，當c?（a，b）時，稱為Cauchy型積分，只要此積分存在。

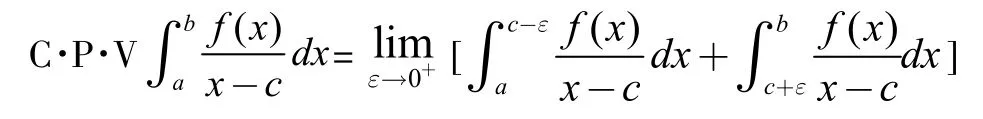
定義2（H?lder條件）設f（x）定義于（a，b）上，若存在常數A，使得對于任意的兩點x1，x2?（a，b），恒有（0

定理1（一階奇異積分的柯西主值存在的充分條件）若f（x）?Ca（a，b），c（a，b），則存在，且

證明：因為

上式右端第二項與第四項之和為：

而右端的第一項與第三項可以如下證明其存在：因為f（x）?Ca（a，b），由H?lder條件，

知

當?→0+時是與?無關的常數，而

此極限一般不存在。

定義3設f（x）?C1，a（a，b），則二階奇異積分的 Hadamard主值為

定理2：設f（x）?C1，a（a，b）（表示f（x）與f（n-1）（x）在（a，b）上都滿足H?lder條件），c?（a，b），則高階奇異積分的Hadamard主值為：

我們還可以將奇點位于區間內部的高階奇異積分的Hadamard主值繼續推廣，討論奇點位于區間邊界處的奇異積分的Hadamard主值。

上式中的第一項極限存在，第二項為常數。但第三項可能不存在。可見單邊一階奇異積分的柯西主值不一定存在，我們刪去引起積分發散的項，即可得到一階單邊積分的Hadamard主值。

定義4設f（x）?ca（a，b），則奇異積分的Hadamard主值為：

只要重復多次使用分部積分法，把引起積分發散的項一概刪去，即可得到單邊高階奇異積分主值。

定理3：設函數f（x）?Cn-1，a（a，b），單邊高階奇異積分主值為：

聯系前面高階奇異積分與以上單邊奇異積分易得以下定理：

定理4：設函數f（x）?Cn-1，a（a，b），c?（a，b），則：

其中左端理解為高階奇異積分，右端為單邊高階奇異積分。

數學分析對發散的廣義積分的研究以判斷出其發散為終止，而問題到此并未圓滿結束，主值問題的提出正是為廣義積分的研究開拓了新的思路，有其不容忽視的作用。

參考文獻

［1］路見可.解析函數邊值問題［M］.上海科學技術出版社，1987.

［2］李子植.函數論的邊值問題［M］.河北大學出版社，2000.

［3］高紅亞.二維高階奇異積分［J］.寧夏大學學報，1996.

［4］高紅亞.多奇點二維高階奇異積分［J］.河北省科學院學報，1996.

［5］高紅亞.無界域上的高階奇異積分與推廣留數定理［J］.河北省科學院學報，1996.

Abstrat:This paper studies the problem of principal value of singular integrals in real number field.This is the improvement research based on the study of generalized integralof Mathematical Analysis.The definitions of Cauchy principal value and Hadamard principal value ofone-dimensional singular integral are obtained，and the formulas are given.

中圖分類號：O17

文獻標志碼：A

文章編號：2096-000X（2016）12-0258-02

作者簡介：孫蘭香（1969，3-），女，漢族，籍貫：河北海興，職稱：副教授，學位：碩士，研究方向：基礎數學。