高考“數(shù)學史料題”的賞析與啟示

陳雪蓮+王新宏

摘 要：每年高考試題中都有一定數(shù)量的“數(shù)學史料題”，它們背景新穎、內(nèi)涵深刻、立意深遠、意雋味濃，使數(shù)學的文化性、應(yīng)用性和理論性有機結(jié)合，成為高考一道靚麗的風景線.它們不但豐富了高考命題的素材，也為當前課改引領(lǐng)了一個方向，更激發(fā)了莘莘學子的數(shù)學興趣，培養(yǎng)了他們的數(shù)學創(chuàng)新能力，也為他們逐步形成正確的數(shù)學觀與價值觀提供了幫助.

關(guān)鍵詞：高考；數(shù)學史；文化；意義；賞析

數(shù)學是人類文明的火車頭，數(shù)學史是人類文化的重要組成部分.2003年頒布的《普通高中數(shù)學課程標準（實驗）》在關(guān)于課程的基本理念中，明確指出要體現(xiàn)數(shù)學史的文化價值：數(shù)學課程應(yīng)適當反映數(shù)學的歷史、應(yīng)用和發(fā)展趨勢；數(shù)學對推動社會發(fā)展的作用；數(shù)學科學的思想體系；數(shù)學的美學價值；數(shù)學家的創(chuàng)新精神.

隨著課程改革的不斷深入，數(shù)學的人文價值更明顯地凸顯出來，已普遍受到重視.縱觀最近幾年全國各地的高考，出現(xiàn)了一些以數(shù)學史為載體的高考試題，成為新課改理念下高考改革和發(fā)展的一道靚麗風景.尤其是湖北省，已經(jīng)連續(xù)多年命制此類考題，逐漸形成了湖北高考數(shù)學卷的一大特色和亮點.這一方面是為學生在平時學習時關(guān)注數(shù)學史提供導向，另一方面數(shù)學史作為一種數(shù)學文化走進高考，讓高考試卷平添了幾分文化色彩與氣息；使高考試卷不再是“枯燥無味”“冰冷”的“人才考查”的一個工具，而是有趣有味的人文作品，讀之賞心悅目，思之奧妙無窮，回味之意猶未盡.

一、試題掃描

查閱了近年來的高考數(shù)學試卷后發(fā)現(xiàn)：幾乎每年都會出現(xiàn)與數(shù)學史相關(guān)的試題，涉及數(shù)學題材的內(nèi)容極為豐富，如古老的“畢達哥拉斯數(shù)”“回文數(shù)”“阿波羅尼斯圓”“秦九韶算法”以及古籍文獻中的立體幾何的相關(guān)問題等（見表1）.

高考試卷的題型有選擇、填空、解答及推演論證，以期通過運用數(shù)學史來考查學生的學習能力、邏輯推理能力、分析問題與解決問題的能力.

二、案例賞析

現(xiàn)遴選4個與數(shù)學史相關(guān)的高考題供賞析.

（一） 畢達哥拉斯圖形數(shù)顯風采

畢達哥拉斯是古希臘著名的哲學家與數(shù)學家，他所創(chuàng)建的畢達哥拉斯學派，是在眾多的數(shù)學學派中對“形數(shù)”的研究最為突出的學派，該項研究強烈地反映了他們將數(shù)作為幾何思維元素的精神，有效地印證了“凡物皆數(shù)”的觀點.

例1 （2012年湖北文科第17題）傳說古希臘畢達哥拉斯學派的數(shù)學家經(jīng)常在沙灘上畫點或用小石子表示數(shù).他們研究過如圖1所示的三角形數(shù)：

將三角形數(shù)1，3，6，10，…記為數(shù)列{an}，將可被5整除的三角形數(shù)按從小到大的順序組成一個新數(shù)列{bn}.可以推測：

（1）b2012是數(shù)列{an}中的第______項；

（2）b2k-1=______.（用k表示）

畢達哥拉斯學派中的數(shù)學家非常喜歡用形表示數(shù)，如：他們曾用圖2形象地說明（1+2+…+n）2=13+23+…+n3.

（二）對稱美回文數(shù)

“回文”是我國古典文學作品中的一種有趣的特殊體裁，有回文詩、回文聯(lián)等.回文的特點是：在一篇作品中，作者精心挑選字詞，巧妙地安排順序，使得一篇作品倒過來從頭讀起，也同樣是有意義的作品，如“云邊月影沙邊雁，水外天光山外樹”，倒過來讀，便是“樹外山光天外水，雁邊沙影月邊云”，其意境和韻味讀來真是一種享受！數(shù)學與文學有著相似之處，在數(shù)學中也有“回文數(shù)”，如121，2002，12321，回文仍是原數(shù).在數(shù)學里，無論從左讀到右還是從右讀到左，都是同一個數(shù)的正整數(shù)稱為回文數(shù).

例2 （2012年湖北理科第13題）回文數(shù)是指從左到右讀與從右到左讀都一樣的正整數(shù).如22，121，3443，94249等.顯然二位回文數(shù)有9個：11，22，33，…，99.三位回文數(shù)有90個：101，111，121，…，191，202，…，999.則：

（Ⅰ）4位回文數(shù)有 個；

（Ⅱ）2n+1（n∈N+）位回文數(shù)有 個.

解析 （Ⅰ）4位回文數(shù)只用排列前面兩位數(shù)字，后面數(shù)字就可以確定，但是第一位不能為0，有9（1～9）種情況，第二位有10（0～9）種情況，所以4位回文數(shù)有9×10=90種.

（Ⅱ）法一：由上面多組數(shù)據(jù)研究發(fā)現(xiàn)，2n+1位回文數(shù)和2n+2位回文數(shù)的個數(shù)相同，所以可以算出2n+2位回文數(shù)的個數(shù).2n+2位回文數(shù)只用看前n+1位的排列情況，第一位不能為0有9種情況，后面n項每項有10種情況，所以個數(shù)為9×10n.

法二：可以看出二位數(shù)有9個回文數(shù)，三位數(shù)90個回文數(shù).計算四位數(shù)的回文數(shù)是可以看出在2位數(shù)的中間添加成對的“00，11，22，…，99”，因此四位數(shù)的回文數(shù)有90個，按此規(guī)律推導S2n=10S2n-2，而當奇數(shù)位時，可以看成在偶數(shù)位的最中間添加0～9這十個數(shù)，因此S2n=10S2n，則答案為9×10n.

回文數(shù)體現(xiàn)了數(shù)學背景下的對稱之美，回文數(shù)有趣而美妙的性質(zhì)有：

（1）除了11，1331以外，所有回文數(shù)的位數(shù)都是奇數(shù).

（2）在完全平方數(shù)、完全立方數(shù)中的回文數(shù)，其比例要比一般自然數(shù)中回文數(shù)所占的比例大得多；例如112=121，222=484，73=343，113=1331，都是回文數(shù).

（3）人們至今未能找到四次方、五次方以及更高次冪的回文素數(shù)；于是數(shù)學家們猜想：不存在nk（k≥4，k，n∈N*）形式的回文數(shù).

（三）魅力阿波羅尼斯圓

一般地，平面內(nèi)到兩定點的距離之比為常數(shù)λ（0<λ≠1） 的動點的軌跡是圓，這個圓叫作阿波羅尼斯圓；阿波羅尼斯是繼歐幾里得、阿基米德之后的又一代著名數(shù)學家，他們?nèi)齻€并稱為亞歷山大時期的數(shù)學三巨匠.以阿波羅尼斯圓為背景的高考試題屢見不鮮，據(jù)統(tǒng)計，在近十年高考中，出了13道考題，阿波羅尼斯圓的魅力體現(xiàn)得淋漓盡致.

解析3（特殊點）

既然對圓O上任意一點M，都有|MB|=λ|MA|，使得λ與b為常數(shù)，那么我們何不把點M取為特殊點呢？取M（1，0）與M（0，1）代入|MB|=λ|MA|得：b2+1=5λ2，（b-1）2=9λ2，得b=-，λ=.

點評 大部分考生想不到特殊化的數(shù)學思想解題，主要原因是他對特殊與一般的數(shù)學思想理解得不夠深刻，不夠到位，再加上平時訓練得又較少甚至沒有，故想不到簡便的解題策略.

高考源于教材，高于教材，阿波羅尼斯圓的身影就在我們的教材中：（人教A版必修2習題4.1 B組第3題）已知點M（x，y）與兩個定點O（0，0），A（3，0）的距離之比，求點M的軌跡方程.

（四）古色古香中國古文獻

據(jù)不完全統(tǒng)計，幾乎每一年都有以我國古代數(shù)學名著如《九章算術(shù)》《數(shù)術(shù)九章》《算數(shù)書》等為素材命制的中國古文化高考真題.它們大多與體積有關(guān)，以古代社會人們的生活實際和生產(chǎn)實際為背景（對考生來說比較陌生與新穎），并且是用古漢語描述的.這就要求考生懂一定量的古漢語知識，能從試題的字里行間挖掘出數(shù)學要素，不斷地經(jīng)歷直觀感知，觀察分析，歸納類比，空間想象，抽象概括，數(shù)據(jù)處理，運算求解.反思與建構(gòu)等思維過程，這一方面，引導考生對題目中所蘊含的數(shù)學知識、方法進行提取、推理、思考、判斷是考生解決問題能力的體現(xiàn)，但另一方面我們也不得不驚嘆古人的聰明、睿智以及對數(shù)學問題用古漢語詩意般的精彩論述.

例4 （2013年湖北文科第16題）我國古代數(shù)學名著《數(shù)書九章》中有“天池盆測雨”題：在下雨時，用一個圓臺形的天池盆接雨水. 天池盆盆口直徑為二尺八寸，盆底直徑為一尺二寸，盆深一尺八寸. 若盆中積水深九寸，則平地降雨量是 寸.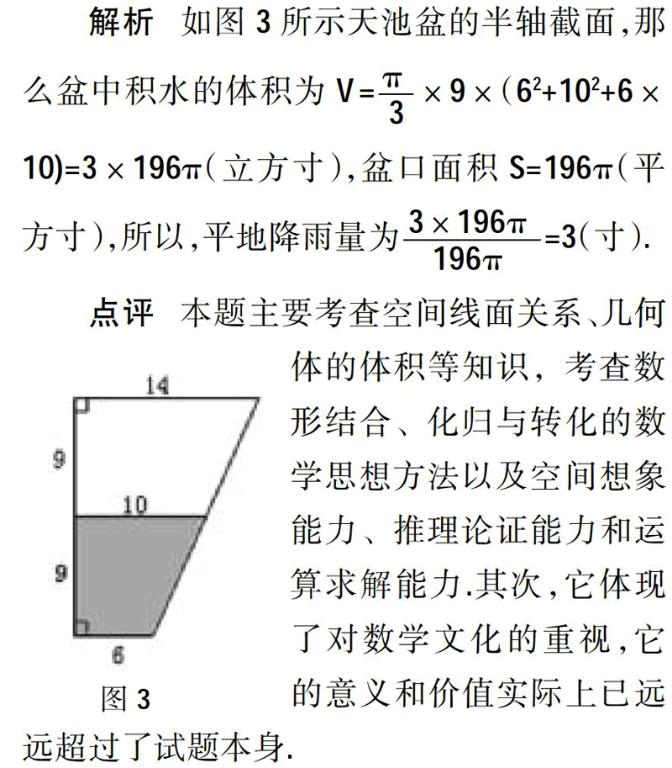

解析 如圖3所示天池盆的半軸截面，那么盆中積水的體積為V=×9×（62+102+6×10）=3×196π（立方寸），盆口面積S=196π（平方寸），所以，平地降雨量為=3（寸）.

點評 本題主要考查空間線面關(guān)系、幾何體的體積等知識，考查數(shù)形結(jié)合、化歸與轉(zhuǎn)化的數(shù)學思想方法以及空間想象能力、推理論證能力和運算求解能力.其次，它體現(xiàn)了對數(shù)學文化的重視，它的意義和價值實際上已遠遠超過了試題本身.

從以上可以看出，關(guān)注數(shù)學史、數(shù)學文化以及數(shù)學科普知識，對我們有著一定的導向作用，教育功能，以及非常重要的現(xiàn)實意義；它們在一定程度上展示了原本數(shù)學的美，傳達了一種勇于探索、鍥而不舍的數(shù)學精神.因此，高考對數(shù)學史與數(shù)學文化的母子、親情關(guān)系另眼相看，它們也一定會引領(lǐng)我們的日常教學，創(chuàng)建富有數(shù)學文化魅力的靈動課堂，讓學生陶醉在數(shù)學史的歷史長河中，享受在數(shù)學文化對人類文明的貢獻中，真切體會數(shù)學的美、數(shù)學的精神、數(shù)學的偉大所在.

三、啟示

（一）體現(xiàn)穩(wěn)定與創(chuàng)新并舉

高考數(shù)學一直在貫徹堅持穩(wěn)定為主，注重基礎(chǔ)考查，突出能力立意，著力內(nèi)容創(chuàng)新，不一味迎合中學數(shù)學教學模式.因此，從實際出發(fā)，結(jié)合學生的實際與考試效度的需要，兼顧公平性與創(chuàng)新性，選擇恰當?shù)膸в腥宋男缘摹皵?shù)學史料題”便順理成章了.

（二）為教學改革鋪磚墊瓦

高考中的數(shù)學史料題，素材新穎、構(gòu)思精巧、立意高遠、意雋味濃、視角獨特、導向鮮明等特點都充分體現(xiàn)了新課改的理念.

高考試題中蘊含數(shù)學史料題的深意，絕不單純是“秀”幾道高考題這么簡單.中學教師應(yīng)加強數(shù)學史對數(shù)學課改的影響，為此教學中應(yīng)該重視數(shù)學史的教學與反思.運用歷史發(fā)生教學原理，不僅可以啟發(fā)學生思維，幫助學生掌握學科體系，而且可以激發(fā)學生的學習興趣，培養(yǎng)學生的探究能力；因此在開展數(shù)學教學時，應(yīng)當適當了解歷史上相關(guān)問題的發(fā)展過程，分析哪些困難可以通過數(shù)學史的途徑加以克服，然后再根據(jù)學生的需要設(shè)計教學，這樣做，可使數(shù)學史的應(yīng)用深入到學生的認知層面，有利于培養(yǎng)學生的數(shù)學思維能力和數(shù)學問題意識.

可以預見，數(shù)學史是一座有待開發(fā)的寶山，有待于我們從多角度、多方位進一步開發(fā)，進而引導高中數(shù)學教學和評價方式的改變，為教學改革鋪磚墊瓦.

（三）增強了數(shù)學的育人功能

數(shù)學教育是數(shù)學文化的教育，而數(shù)學史是數(shù)學文化的重要載體，通過對數(shù)學家發(fā)現(xiàn)問題、發(fā)明方法、創(chuàng)造思想的了解，可以激發(fā)學生學習數(shù)學的興趣，從而培養(yǎng)學生的創(chuàng)造精神和創(chuàng)新能力；另一方面，數(shù)學科學的思想體系、數(shù)學的美學價值、數(shù)學家的創(chuàng)新精神、數(shù)學在人類文明發(fā)展中的作用，都將有利于學生逐步認識真實的數(shù)學以及形成正確的數(shù)學觀和價值觀.