考慮轉速濾波的永磁同步電動機轉速伺服系統改進型自抗擾控制器

左月飛　符　慧　劉　闖　張　捷　胡　燁

(南京航空航天大學自動化學院　南京　210016)

?

考慮轉速濾波的永磁同步電動機轉速伺服系統改進型自抗擾控制器

左月飛符慧劉闖張捷胡燁

(南京航空航天大學自動化學院南京210016)

摘要在永磁同步電動機伺服系統中，通常根據位置信號采用M法計算轉速。由于位置信號存在量化誤差等原因，計算轉速存在測量噪聲，因此常將濾波后的轉速作為反饋。在傳統的轉速一階自抗擾控制系統中，自抗擾控制器的設計過程并未考慮轉速濾波環節的影響，這將使系統性能受濾波時間常數的影響。提出一種考慮反饋轉速濾波環節的改進型自抗擾控制器，將濾波后的轉速擴張為一個新狀態量，利用三階線性擴張狀態觀測器估計濾波之前的轉速量，并將其作為反饋。實驗結果表明，改進型自抗擾控制系統具有較好的控制性能。

關鍵詞：永磁同步電動機自抗擾控制轉速計算測量噪聲濾波器擴張狀態觀測器

0引言

永磁同步電動機(Permanent Magnet Synchrounous Motor，PMSM)以其高功率/重量比、高轉矩/慣量比、高效率和具有一定魯棒性等優點逐漸取代直流電機和其他電勵磁的電動機，在中小功率高精度轉速伺服系統中被廣泛應用。在航空航天、機器人、數控機床等領域，通常要求電動機轉速伺服系統具有快速準確的響應，且受到外界擾動后能夠快速恢復。傳統的線性PI控制難以滿足高性能的要求。

隨著永磁同步電動機非線性控制理論的發展，多種先進的復雜控制策略如自適應控制[1，2]、模糊控制[3]、滑模變結構控制[4，5]等被應用于轉速伺服系統。盡管這些方法最終都能抑制擾動，但其依靠反饋控制，動態過程非常緩慢。一種有效提高擾動抑制效果的方法是通過擾動觀測器(Disturbance Observer，DOB)對擾動進行觀測并前饋補償，這一思路最先由日本學者K.Ohnishi[6]提出。順著這一思路，眾多基于DOB的控制方法相繼得到應用[7，8]。與DOB具有相同功能的另一種觀測器為擴張狀態觀測器(Extended State Observer，ESO)，它將內部擾動和外部擾動一起作為集總擾動，并將其擴張成一個新的狀態，因此此狀態觀測器比常規的狀態觀測器要多一個狀態。ESO可同時對狀態和擾動進行觀測。基于ESO觀測的擾動進行前饋補償的控制方法稱為自抗擾控制(Active Disturbance Rejection Control，ADRC)[9]，該方法已在PMSM控制中得到越來越多的應用[10-12]。

實際系統中，轉速通常根據位置信號采用M法計算得到。由于數字控制系統中存在量化誤差等原因，計算轉速通常存在測量噪聲，且測量噪聲隨轉速的減小而增大，因此通常對測量轉速進行濾波，并將濾波后的轉速作為反饋信號。在傳統的PMSM轉速一階ADRC系統中，自抗擾控制器的設計過程中并未考慮轉速濾波環節的影響，因此通常采用二階線性ESO，這會對系統控制性能產生影響。針對輸出的測量值存在噪聲的問題，文獻[13]提出采用Fal函數濾波器代替傳統的一階線性濾波器對測量值進行濾波，通過非線性濾波器實現在相同濾波效果下的相位滯后較小，但并未解決相位滯后問題，且該濾波器存在參數調節復雜的問題。文獻[14]提出擴展一階狀態到ESO的方法，即將測量信號的積分值擴展一個新的狀態，而后以此構建對應的ESO，該方法存在積分值飽和的問題。文獻[15]提出擴展濾波器方程到ESO中的方法，較好地解決了原狀態無法觀測的問題，但文中采用了非線性ESO，參數整定比較困難。

本文針對PMSM轉速一階ADRC系統，采用線性一階低通濾波器對計算轉速進行濾波，而后將濾波后的轉速擴張為一個新的狀態量，將轉速環變為一個二階系統，采用三階線性ESO對濾波前轉速進行觀測，并將其作為反饋，構建了改進型自抗擾控制系統，改善了系統的控制性能。最后在dSPACE半實物仿真平臺上驗證了理論分析的正確性。

1傳統自抗擾控制器的設計

1.1PMSM轉速環數學模型

(1)

式中，J為系統的轉動慣量，kg·m2；B為系統的粘滯摩擦系數，N·m·s/rad；TL為負載轉矩，N·m；Ω為機械角速度，rad/s；Kt為轉矩常數，N·m/A；iq為交軸電流，A。

由式(1)可得機械角速度狀態方程為

(2)

選取機械角速度Ω為狀態變量x1，將交軸電流iq作為控制量u，將擾動d(t)擴張為狀態變量x2，假設其在一個采樣周期內保持不變，則狀態方程變為

(3)

定義y1為狀態x1的測量值，包含實際狀態x1與狀態的測量噪聲δns，即y1=x1+δns。為減小噪聲，通常將濾波后的測量值作為反饋。假設采用時間常數為Tfdb或截止頻率為ωc的一階低通濾波器，則濾波后的狀態量x0為

(4)

式中，Tfdbωc=1，Tfdb=0 ms表示反饋通道無濾波。

于是，系統的狀態方程變為

(5)

1.2反饋控制律設計

定義機械角速度給定值Ω*為v，角速度跟蹤誤差es=v-x1，則跟蹤誤差狀態方程為

(6)

采用線性比例反饋控制律，即

(7)

式中，kps為控制器的比例系數。

結合式(6)和式(7)可得系統控制量為

(8)

采用式(8)所示的控制量時，系統可簡化為一個積分器系統，且跟蹤誤差按式(7)所示的規律衰減。然而，式(8)中的實際狀態x1和實際擾動x2無法知曉，只能通過測量或用觀測器觀測得到。

1.3不考慮轉速濾波的線性ESO

對系統(3)構建二階線性ESO，如式(9)所示，其結構框圖如圖1所示。

(9)

式中，z1和z2分別為狀態量x0和x2的估計值；e1為ESO對x0的觀測誤差；β1、β2為觀測器系數。

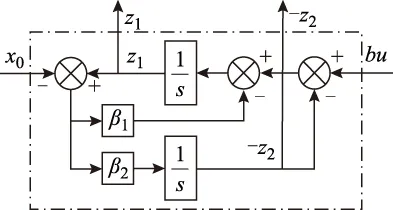
圖1　二階線性ESO結構框圖Fig.1　Block diagram of 2nd-order

由式(9)可得ESO輸出z1、z2與輸入x0、bu的關系為

(10)

式中，λ2(s)=s2+β1s+β2為ESO的特征多項式。

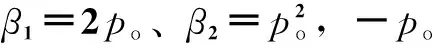
由式(10)可看出，ESO對階躍擾動具有漸進收斂性。將式(8)中的x1、x2分別用z1、z2代替，得到理論控制量u與實際控制量u1分別為

(11)

(12)

綜上可得轉速環一階自抗擾控制器的結構框圖如圖2所示，永磁同步電動機轉速一階自抗擾控制系統的簡化結構框圖如圖3所示。

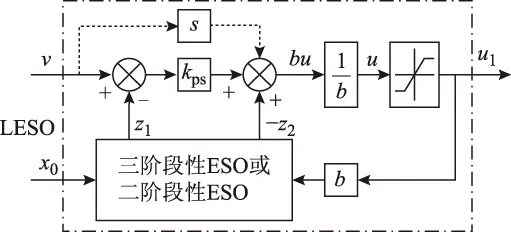
圖2　轉速環一階自抗擾控制器Fig.2　First-order ADRC controller of speedloop

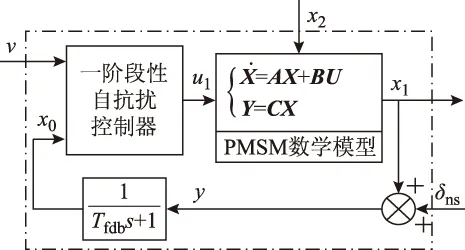
圖3　轉速自抗擾控制系統結構框圖Fig.3　Block diagram of the speed loop ADRC system

1.4傳統自抗擾控制系統的響應

為分析方便，以下分析過程中忽略電流跟蹤誤差和電流限幅的影響。由式(10)、式(11)可得

(13)

式中，傳遞函數G1(s)、G2(s)、G3(s)的表達式分別為

(14)

定義Gf(s)=Tfdbs+1，則由式(5)、式(13)可得閉環系統的輸出為

[x2(s)+sδns(s)]

(15)

式中，Γ1=sG1(s)Gf(s)+G2(s)=Tfdbs2G1(s)+G3(s)為閉環系統的特征多項式。

當無輸入微分前饋或輸入微分前饋不起作用時，系統在給定v(s)作用下的傳遞函數將變為

(16)

由式(15)和式(16)可看出，傳統的自抗擾控制系統的跟蹤性能、抗擾性能以及抑制測量噪聲性能均受濾波時間常數的影響。

2考慮轉速濾波的改進型自抗擾控制器

2.1考慮轉速濾波的線性ESO

對系統(5)構建三階線性ESO，如式(17)所示，其結構框圖如圖4所示。

(17)

式中，z0、z1和z2分別為狀態量x0、x1和x2的估計值；e0為ESO對x0的觀測誤差；β0、β1和β2為觀測器系數。

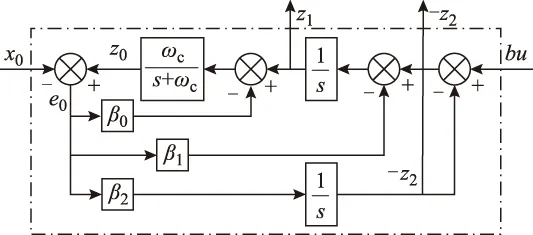
圖4　三階線性ESO結構框圖Fig.4　Block diagram of 3rd-order LESO

由式(17)可得ESO輸出z1、z2與y1、bu的關系為

(18)

式中，λ3(s)=[Gf(s)+β0]s2+β1s+β2為ESO的特征多項式。由式(10)和式(11)可得

(19)

式中，傳遞函數G1(s)、G2(s)、G3(s)的表達式分別為

(20)

由式(5)和式(19)可得閉環系統的輸出為

(21)

當無輸入微分前饋或輸入微分前饋不起作用時，系統在給定v(s)作用下的傳遞函數將變為

(22)

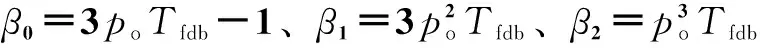
(23)

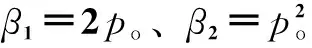
由式(21)～式(23)可知，改進型自抗擾控制系統的跟蹤性能、抗擾性能以及抑制測量噪聲性能均不再受濾波時間常數的影響。

為便于描述，定義采用二階線性ESO的控制系統為傳統自抗擾控制系統(以下簡稱傳統系統)，采用三階線性ESO的系統為改進型自抗擾控制系統(以下簡稱新系統)。

2.2新系統的性能分析

2.2.1新系統的跟蹤性能

根據輸入微分前饋能否起作用將系統輸入分為可微分前饋型輸入和不可微分前饋型輸入兩類。考慮到分析典型性，分別以非連續變化的階躍輸入和連續變化的正弦輸入為例進行分析。

當系統輸入為正弦信號時，輸入的微分為余弦信號，由此產生的電流給定也為余弦信號，此時可忽略電流跟蹤誤差，即輸入微分前饋能夠起作用。由式(21)可看出，系統在無擾動的情況下能夠完全跟蹤可微分前饋型輸入。

當系統輸入為階躍信號時，輸入的微分為脈沖信號，由此產生的電流給定也為脈沖信號，通常實際電流無法響應，輸入微分前饋的作用可忽略，系統在給定v(s)作用下的閉環傳遞函數如式(22)所示。式(22)表明系統在無擾動下的階躍響應惟一取決于比例系數kps，kps越大，則階躍響應越快。

2.2.2新系統的抗擾性能

由式(21)可得系統在擾動x2(s)作用下的傳遞函數為

(24)

當po=500，kps=36，Tfdb分別為0 ms、0.1 ms和1.0 ms時，系統(24)的頻域特性曲線如圖5所示。由圖5可看出，新系統在轉速存在濾波時的抗擾性能不受反饋通道濾波器的影響，但要比無濾波時的稍差。

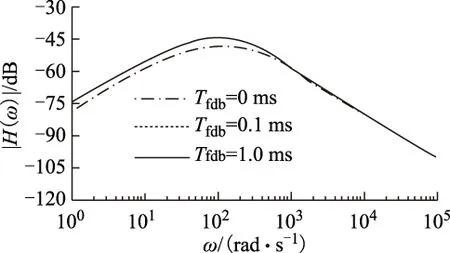
圖5　抗擾系統的頻域特性曲線Fig.5　Bode diagram of the disturbance rejecting system

2.2.3新系統的抑制測量噪聲特性

由式(19)和式(20)可得系統的測量噪聲到控制量和輸出的傳遞函數為

(25)

(26)

當po=500，kps=36，Tfdb分別為0 ms、0.1 ms和1.0 ms時，式(25)和式(26)的頻域特性曲線如圖6所示。由圖6可看出，新系統在Tfdb=0.1 ms和Tfdb=1.0 ms時的抑制測量噪聲相同，且比Tfdb=0 ms時的抑制測量噪聲性能好。

綜上所述，新系統在轉速存在濾波時，其性能不受濾波時間常數的影響，且相比于轉速無濾波時，其抗擾性能稍差，但抑制測量噪聲性能較好，而跟蹤性能則無差別。由于新系統具有較好的濾波性能，故可通過適當增大ESO的帶寬po來犧牲一些抑制噪聲性能以獲得更好的抗擾性能。

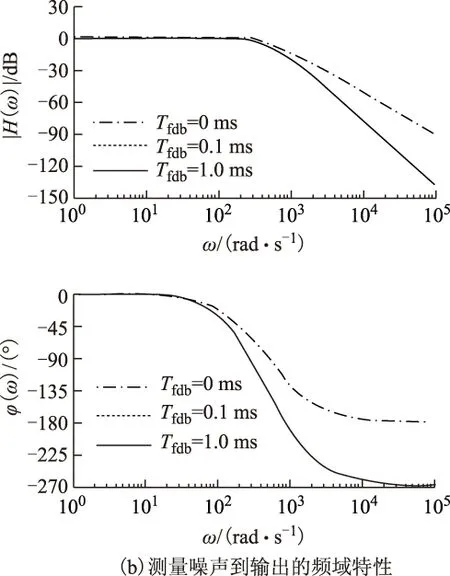
圖6　新系統的抑制測量噪聲特性Fig.6　Noise characteristics of the novel ADRC system

3實驗驗證

為驗證理論分析的正確性，在永磁同步電動機轉速伺服系統中對算法進行了實驗驗證。實驗中所用的PMSM參數如表1所示。

表1　電機參數

永磁同步電動機調速系統的實驗平臺采用基于dSPACE實時仿真系統DS1103，利用快速原型法通過Simulink自動完成代碼的生成與下載。實驗中的逆變器開關頻率為10 kHz，通過PWM中斷觸發電流采樣和占空比的更新。轉速環和電流環采樣周期以及系統的計算步長均為0.1 ms。兩個電流環均采用PI控制，電流環帶寬為2 000 rad/s。

3.1新系統的跟蹤性能

設置po=500，kps分別為36和360，Tfdb分別為0 ms、1 ms和5 ms。在不同kps和Tfdb組合下，轉速給定由0 r/min階躍變化至800 r/min和200 r/min時的實驗波形分別如圖7和圖8所示。

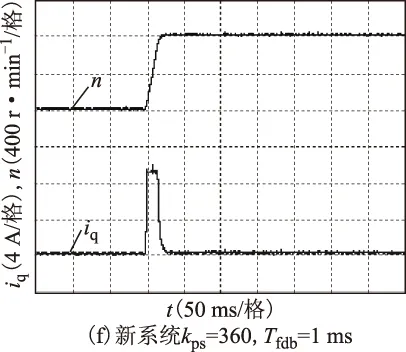
圖7　空載起動時的800 r/min階躍響應Fig 7　800 r/min step response when starting with no-load

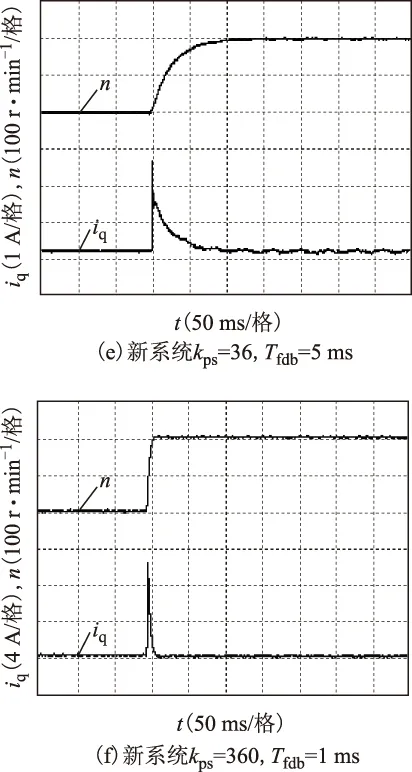
圖8　空載起動時的200 r/min階躍響應Fig.8　200 r/min step response when starting with no-load

圖7a～圖7d為傳統系統下的響應曲線，圖7e～圖7f為新系統下的響應曲線。對比圖7a和圖7b可看出，Tfdb由0 ms變為1 ms可減小系統噪聲且幾乎不影響系統性能。對比圖7b和圖7c可知，Tfdb為1 ms時，kps由36變為360會使傳統系統的階躍響應產生振蕩。對比圖7b和圖7d可知，kps為36時，Tfdb由1 ms增大至5 ms也會使傳統系統的階躍響應產生振蕩。分別對比圖7d和圖7e、圖7c和圖7f可知，新系統的階躍響應不受濾波時間常數的影響。

對比圖7和圖8可看出，200 r/min階躍響應與800 r/min階躍響應的不同之處僅在于圖8c中轉速響應出現了超調，而圖7c中轉速響應出現了凹陷，但由兩圖得到的結論是相同的。傳統系統在轉速濾波時可獲得更好的抑制噪聲性能，但會使系統階躍響應產生振蕩，而新系統則可在抑制噪聲的同時不影響階躍響應性能，且適用于不同的濾波時間常數和不同的轉速。

3.2新系統的抗擾性能

實驗中負載曲線如圖9所示，由于加載過程較緩慢，轉速變化不是很明顯，為此只做了卸載實驗。使電動機在帶載2.1 N·m下穩定運行于800 r/min，而后突然卸載，轉速響應波形如圖10所示。

圖9　實驗負載曲線Fig.9　Load curve used in experiment

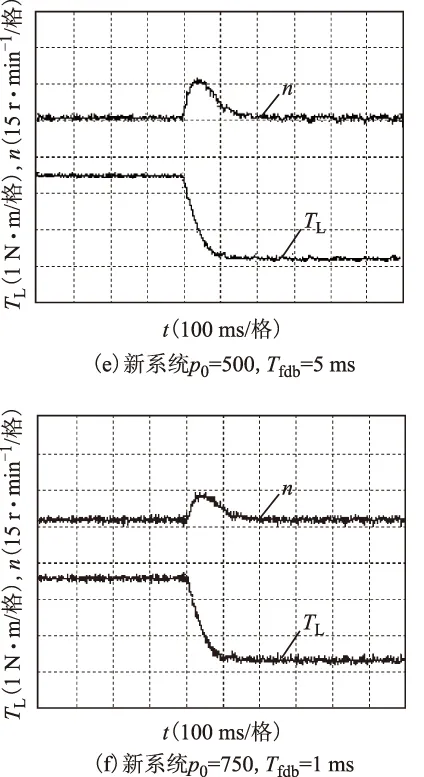
圖10　卸載時的轉速響應Fig.10　Dynamic response of when unloading

綜上所述，對于變化平緩的負載，傳統系統在轉速濾波時可獲得更好的抑制噪聲性能，且其抗擾性能基本不受影響。傳統系統相比于新系統具有更好的抗擾性能。

對比圖10a和圖10b可看出，Tfdb由0 ms變為1 ms可減小系統噪聲且幾乎不影響系統性能。對比圖10b和圖10c可知，Tfdb為1 ms時，po由500增大至750可提高系統的抗擾性能，但也增大了傳統系統的噪聲。對比圖10b和圖10d可知，po為500，Tfdb由1 ms增大至5 ms時，波形中噪聲更小且擾動并未產生變化，這是因為測功機所能提供的負載變化較平緩。由跟蹤性能的實驗結果可知，當負載變化較快時(如階躍負載)，則濾波時間常數也會對總擾動產生影響。

對比圖10a和圖10e可看出，新系統在有轉速濾波時的抗擾性能比無轉速濾波時的差，與理論分析相符。由圖10a和圖10f可看出，新系統通過適當增大ESO的帶寬，可在保證與無濾波時抗擾性能相同的情況下獲得更好的噪聲抑制特性。

4結論

在永磁同步電動機轉速伺服系統中，傳統的轉速一階自抗擾控制器在設計時未考慮轉速濾波環節的影響，這會導致系統的階躍響應產生振蕩。本文將濾波器方程擴展到ESO中，通過ESO觀測濾波之前的轉速，并將其作為反饋，從而消除濾波器對系統性能的影響。

通過擴展濾波器方程到ESO中可提高ESO的系統階數，使ESO具有更好的濾波特性。基于高階ESO的新系統可有效減小系統噪聲，且系統性能不受濾波器時間常數的影響。在ESO帶寬相同的情況下，新系統的抗擾性能不如傳統系統，但其抑制測量噪聲性能比后者好，因此可通過適當提高ESO的帶寬來犧牲一些抑制噪聲性能以獲得更好的抗擾性能。

參考文獻

[1]魯文其，胡育文，梁驕雁，等.永磁同步電機伺服系統抗擾動自適應控制[J].中國電機工程學報，2011，31(7)：75-81.

Lu Wenqi，Hu Yuwen，Liang Jiaoyan，et al.Anti-disturbance adaptive control for permanent magnet synchronous motor servo system[J].Proceedings of the CSEE，2011，31(7)：75-81.

[2]梁驕雁，胡育文，魯文其.永磁交流伺服系統的抗擾動自適應控制[J].電工技術學報，2011，26(10)：174-80.Liang Jiaoyan，Hu Yuwen，Lu Wenqi.Anti-disturbance adaptive control of permanent magnet AC servo system[J].Transactions of China Electrotechnical Society，2011，26(10)：174-180.

[3]張洪帥，王平，韓邦成.基于模糊PI模型參考自適應的高速永磁同步電機轉子位置檢測[J].中國電機工程學報，2014，34(12)：1889-1896.

Zhang Hongshuai，Wang Ping，Han Bangcheng.Rotor position measurement for high-speed permanent magnet synchronous motors based on fuzzy PI MRAS[J].Proceedings of the CSEE，2014，34(12)：1889-1896.

[4]汪海波，周波，方斯琛.永磁同步電機調速系統的滑模控制[J].電工技術學報，2009，27(9)：71-77.

Wang Haibo，Zhou Bo，Fang Sichen.A PMSM sliding mode control system based on exponential reaching law[J].Transactions of China Electrotechnical Society，2009，27(9)：71-77.

[5]張曉光，趙克，孫力，等.永磁同步電機滑模變結構調速系統動態品質控制[J].中國電機工程學報，2011，31(15)：47-52.

Zhang Xiaoguang，Zhao Ke，Sun Li，et al.Sliding mode control of permanent magnet synchronous motor based on a novel exponential reaching law[J].Proceedings of the CSEE，2011，31(15)：47-52.

[6]Ohnishi K.A new servo method in mechatronics Trans[J].Transactions on Japanese Society of Electrical Engineering，1987，107：83-86.

[7]Komada S，Ishida M，Ohnishi K，et al Disturbance observer-based motion control of direct drive motors[J].IEEE Transactions on Energy Conversion，1991，6(3)：553-9.

[8]劉穎，周波，方斯琛.基于改進型擾動觀測器的永磁同步電機滑模控制[J].中國電機工程學報，2010，30(9)：80-85.

Liu Ying，Zhou Bo，Fang Sichen.Sliding mode control of PMSM based on a novel disturbance observer[J].Proceedings of the CSEE，2010，30(9)：80-85.

[9]韓京清.自抗擾控制技術—估計補償不確定因素的控制技術[M].北京：國防工業出版社，2008.

[10]Li Shihua，Xia Cunjian，Zhou Xuan.Disturbance rejection control method for permanent magnet synchronous motor speed-regulation system[J].Mechatronics，2012，22(6)：706-714.

[11]盧達，趙光宙，曲軼龍，等.永磁同步電機無參數整定自抗擾控制器[J].電工技術學報，2013，28(3)：27-34.

Lu Da，Zhao Guangzhou，Qu Yilong，et al.Permanent magnetic synchronous motor control system based on no manual tuned active disturbance rejection control[J].Transactions of China Electrotechnical Society，2013，28(3)：27-34.

[12]Li Shihua，Liu Zhigang.Adaptive speed control for permanent-magnet synchronous motor system with variations of load inertia[J].IEEE Transactions on Industrial Electronics，2009，56(8)：3050-3059.

[13]王宇航，姚郁，馬克茂.Fal函數濾波器的分析及應用[J].電機與控制學報，2010，14(11)：88-91.

Wang Yuhang，Yao Yu，Ma Kemao.Analysis and application of Fal function filter[J].Electric Machine and Control，2010，14(11)：88-91.

[14]宋金來，甘作新，韓京清.自抗擾控制技術濾波特性的研究[J].控制與決策，2003，18(1)：110-112.

Song Jinlai，Gan Zuoxin，Han Jingqing.Study of active disturbance rejection controller on filtering[J].Control and Decision，2003，18(1)：110-112.

[15]林飛，孫湖，鄭瓊林，等.用于帶有量測噪聲系統的改進型擴張狀態觀測器[J].控制理論與應用，2005，22(6)：995-998.Lin Fei，Sun Hu，Zheng Qionglin，et al.Novel extended state observer for uncertain system with measurement noise[J].Control Theory and Application，2005，22(6)：995-998.

作者簡介

左月飛男，1989年生，博士研究生，研究方向為永磁同步電機伺服系統控制。

E-mail：zuo@nuaa.edu.cn(通信作者)

符慧女，1992年生，碩士研究生，研究方向為永磁同步電機伺服系統控制。

E-mail：nuaa031020311@163.com

A Modified Active Disturbance Rejection Controller Concerning Speed Filter for PMSM Speed Servo System

Zuo YuefeiFu HuiLiu ChuangZhang JieHu Ye

(College of AutomationNanjing University of Aeronautics and AstronauticsNanjing210016China)

AbstractIn the permanent magnet synchronous motor (PMSM) servo system，the M-method is usually used to calculate the speed based on the measured rotor angle.As the quantization error exists in the rotor angle，the method produces the measurement noise.As a solution，the filtered speed is taken as the feedback signal.In the conventional first order active disturbance rejection control (ADRC) system，the filter is not concerned in the controller design process，which deteriorates the system performance because of the influence of the time constant of the first order circuit.In this paper，a modified ADRC controller concerning the speed filter is proposed to improve the control performance.The filtered speed is extended as the new state.Then the unfiltered speed is observed by a third order extended observer and taken as the feedback signal.The experiment results indicate that the proposed controller has a better control performance.

Keywords：Permanent magnet synchronous motor，active disturbance rejection control，speed calculation，measurement noise，filter，extended state observer

中圖分類號：TM351

國家自然科學基金(51377076)、江蘇省“六大人才高峰”項目(YPC13013)和江蘇省產學研資金(BY2014003-09)資助。

收稿日期2015-03-03改稿日期2015-05-01