一類特殊行列式的計(jì)算及推廣

侯麗芬

(朔州師范高等專科學(xué)校 數(shù)計(jì)系，山西 朔州 036002)

?

一類特殊行列式的計(jì)算及推廣

侯麗芬

(朔州師范高等專科學(xué)校 數(shù)計(jì)系，山西 朔州 036002)

[摘要]本文通過對例題進(jìn)行分析，由淺入深，對其多種情形進(jìn)行推廣，總結(jié)歸納了這一類型行列式的計(jì)算公式，并給出此公式在行列式計(jì)算中的應(yīng)用.

[關(guān)鍵詞]行列式;加邊法;化三角法;行列式計(jì)算

行列式是《高等代數(shù)》的一個(gè)基本概念，在各個(gè)領(lǐng)域都有廣泛的應(yīng)用，其計(jì)算的重要性也不言而喻.這里通過對例題的推廣，得到一類行列式的各種變形及相應(yīng)的計(jì)算公式，為讀者求解這類行列式提供一些參考．

1例題求解及推廣

:0111101111011110c1+c2+c3+c43111301131013110

上述行列式的各行和相等，且對角線元素全相等，而其余元素全相等.據(jù)此，我們對該行列式推廣到一般情形.

(1)

所以Dn=[a+(n-1)x](a-x)n-1.

(1)中行列式的各行和相等，且對角線元素都相等，若對角線元素不都相等，則有:

推廣2n階行列式

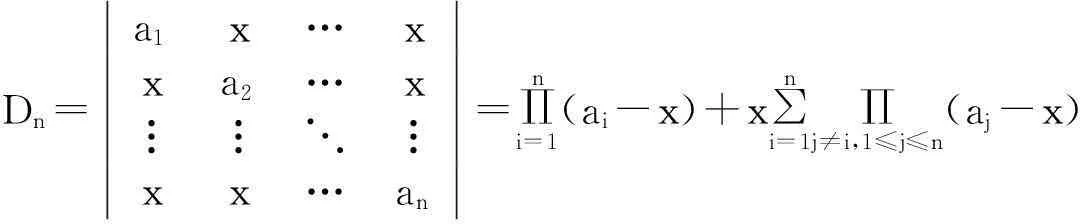
Dn=a1x…xxa2…x????xx…an=∏ni=1(ai-x)+x∑ni=1∏j≠i,1≤j≤n(aj-x)

(2).

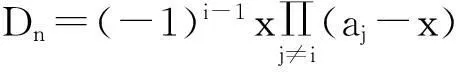
若ai≠x，i=1，2，…，n，應(yīng)用加邊法有

1xx…x0a1x…x0xa2…x?????0xx…an

公式(1)中行列式的各行和相等，且除了對角線以外的元素都相等，若對角線以外的元素不都相等，則有:

推廣3n階行列式

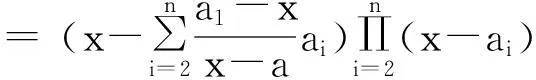
其中 x≠ai(i=1，2， …，n).

(3)

利用化三角法有

xa2a3…ana1-xx-a20…0a1-x0x-a3…0?????a1-x00…xn-an

推廣3中行列式的各行和相等，且對角線上中除對角線上各列相同，若對角線上的元素不都相等，則有:

推廣4n階行列式

(4)

仿照推廣2、3的計(jì)算方法有

1x1x2x3…xn-1a1-x100…0-10a2-x20…0??????-1000…an-xn

1+∑ni=1xia1-xix1x2x3…xn0a1-x100…0-10a2-x20…0??????-1000…an-xn

2公式的應(yīng)用

我們舉例說明上述推廣的應(yīng)用．

解: 由公式(1) 得Dn=[(1+2)n-1]·(1-2) n-1 = (-1)n-1(2n - 1) ．

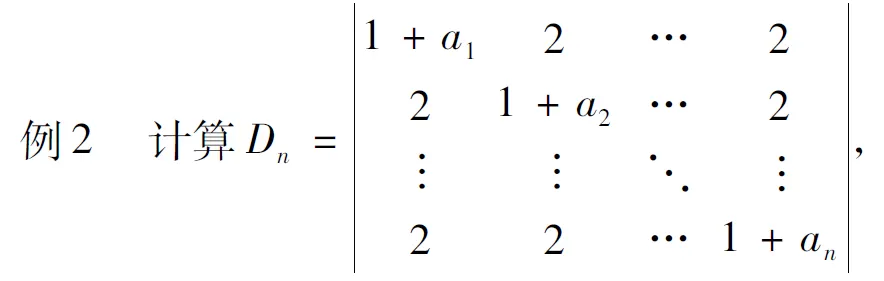
其中a1a2…an≠0．

解: 由公式(3)得

例4計(jì)算

解: 由公式(4)得

3結(jié)束語

行列式的計(jì)算是《高等代數(shù)》的難點(diǎn)內(nèi)容之一.這里通過對一道例題深入挖掘，加以提煉，推廣總結(jié)，得到更為一般性的結(jié)論.通過對例題的計(jì)算、推廣，不僅使學(xué)生得到一些計(jì)算公式，更能夠啟發(fā)學(xué)生的思維，引導(dǎo)學(xué)生自主進(jìn)行探索.

[參考文獻(xiàn)]

[1]王萼芳，石生明.高等代數(shù)(第3版)[M].北京:高等教育出版社，2003.

[2]汪志華.一種特殊類型行列式的計(jì)算及推廣[J].安慶師范學(xué)院學(xué)報(bào)(自然科學(xué)版)，2015，(1):103-105.

[責(zé)任編輯：弓心水]

A kind of special determinant calculation and promotion

HOU Li-fen

(Department of mathematics and Computer science，Shuozhou normal college，Shuozhou 036002,China)

Abstract:Through analysis of examples，this paper is to promote the various circumstances. This type of determinant calculation formula is summarized， and application in the determinant calculation formula is given.

Key words:determinant; Add edge method; The triangular method; The determinant calculation

[收稿日期]2016-01-09

[作者簡介]侯麗芬(1982-)，女，山西晉中人，教師，主要從事泛函分析研究與教學(xué)。

[中圖分類號(hào)]G642

[文獻(xiàn)標(biāo)識(shí)碼]A

[文章編號(hào)]1671-5330(2016)02-0114-03